当前位置：首页 > news >正文

构建AI智能体：三十九、中文新闻智能分类：K-Means聚类与Qwen主题生成的融合应用

news 2025/9/21 7:18:34

一、故事的开端

在讲什么是K-Means时，我们先来讲一个和我们息息相关的小例子，想象一下，我们刚从一个超市回来，买了一大袋杂货零食。然后把这些东西一股脑儿全都倒在了桌子上，现在桌上一片混乱：有苹果、橙子、罐头、饼干、薯片等等。看着有点乱，我们想给他整理一下，放到三个零食收纳盒里去，今天我们当一个精致的收纳小能手，让这个分类变的有意义一点，首先我们不会一眼就精准地分出三堆，常规的操作过程，看看我们会如何去完成。

第一步：随机初始化

首先我们并不知道最终的三堆应该是什么。所以得随机地从桌上抓起三样东西作为“代表”，比如刚好抓了一个苹果、一个罐头和一包薯片。

苹果就是“第一堆”的初始代表。
罐头就是“第二堆”的初始代表。
薯片就是“第三堆”的初始代表。

这一步好比 KMeans 随机选择 K 个点作为初始质心。

第二步：分配步骤

现在，我们开始整理桌上的每一件商品。对于每一件商品，都会做一个决定：

拿起一个橙子：把它和三个代表（苹果、罐头、薯片）比较。
- 橙子和苹果都是水果，很相似，初步估计离“苹果代表”最近。
- 决定：把橙子放到第一堆（苹果堆）里。
拿起一包饼干：继续把它和三个代表比较。
- 饼干和薯片都是零食，很相似，初步估计离“薯片代表”最近。
- 决定：把饼干放到第三堆（薯片堆）里。
拿起一个汤罐头：继续把它和三个代表比较。
- 汤罐头和蔬菜罐头都是罐头，初步估计离“罐头代表”最近。
- 决定：把汤罐头放到第二堆（罐头堆）里。

我们重复这个过程，直到桌上的每一件商品都被分配到了三堆中的某一堆里。

这一步好比 KMeans 计算每个数据点到各个质心的距离，并将其分配到最近的质心所在的簇。

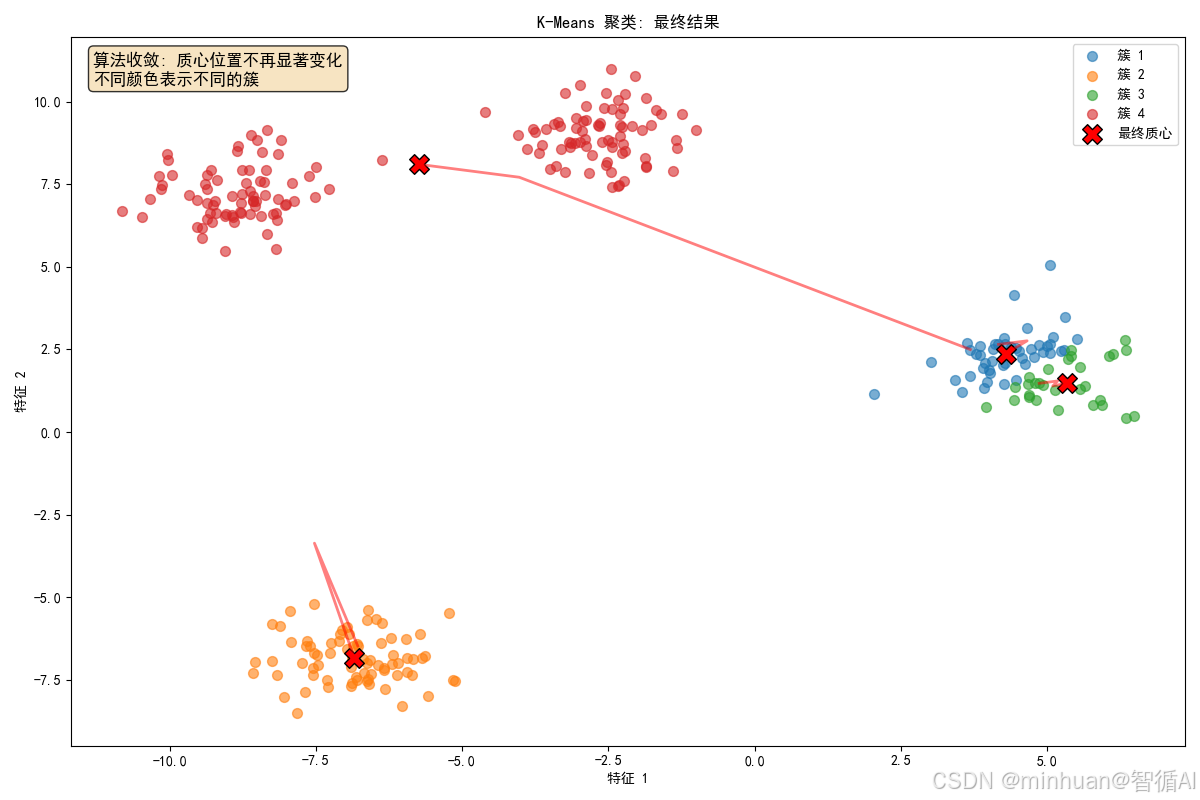
第三步：更新步骤

现在，所有商品都分完了，但每个分类的代表还是最初随机抓的那三样。这显然不准确。比如第一堆里现在有很多水果（苹果、橙子、香蕉），但代表只有一个苹果。

所以，我们重新定义每一堆的“代表”。

首先看一眼第一堆水果堆，觉得这一堆的核心是水果。于是用这一堆里所有商品的平均概念来代表它，或者说，在心里把代表从“一个苹果”更新成了“水果”这个概念。
同样地，你把第二堆的代表从“一个罐头”更新为“罐头食品”。
把第三堆的代表从“一包薯片”更新为“零食包装袋”。

这一步好比 KMeans 重新计算每个簇的质心，取簇内所有点的平均值。

第四步：迭代与收敛

我们仔细观察后发现，因为代表变了，之前的一些分配现在看起来可能不太对了。

比如有一盒果汁，之前被分到了“零食堆”（因为和薯片、饼干放在一起），但现在“水果堆”的代表是“水果”，果汁显然和水果更相似。
所以，我们又重新开始分配，通过第二步的方式，根据新的代表（水果、罐头食品、零食）来重新检查每一件商品应该属于哪一堆。

经过不断地重复“分配”和“更新代表”这两个步骤，直到后来发现，无论我们再怎么检查，所有商品都已经待在它最该待的那一堆里了，代表的定义也不再发生变化。

此时，算法收敛，任务完成！我们成功地将杂乱的商品分成了三个有意义的簇：

簇一：水果（苹果、橙子、香蕉...）
簇二：罐头食品（蔬菜罐头、汤罐头、肉罐头...）
簇三：零食（薯片、饼干、糖果...）

我们以上的做法就和 KMeans 算法一模一样，通过这个例子，我们可以理解 K-Means 的这几个核心特性和挑战：

必须指定 K：我们一开始就要决定分几堆（K=3）。如果我们决定分 4 堆，结果可能完全不同，比如把饮料单独分出来。
随机初始化的影响：如果我们最开始随机抓的代表是苹果、橙子、香蕉，这三个都是水果，那开局就全乱了，最终结果可能很糟糕。这就是为什么需要 K-Means++ 这种更聪明的初始化方法。
迭代过程：算法不是一步到位的，它通过不断“分配-更新”来逐步优化结果。
最终结果：算法会给你分好的堆（簇），以及每一堆的核心代表（质心）。

所以，K-Means 的本质就是一个自动化的“归纳整理”工具，它试图在数据中找到最自然的分组，让组内成员尽可能相似，组间成员尽可能不同。

简洁的流程图理解：

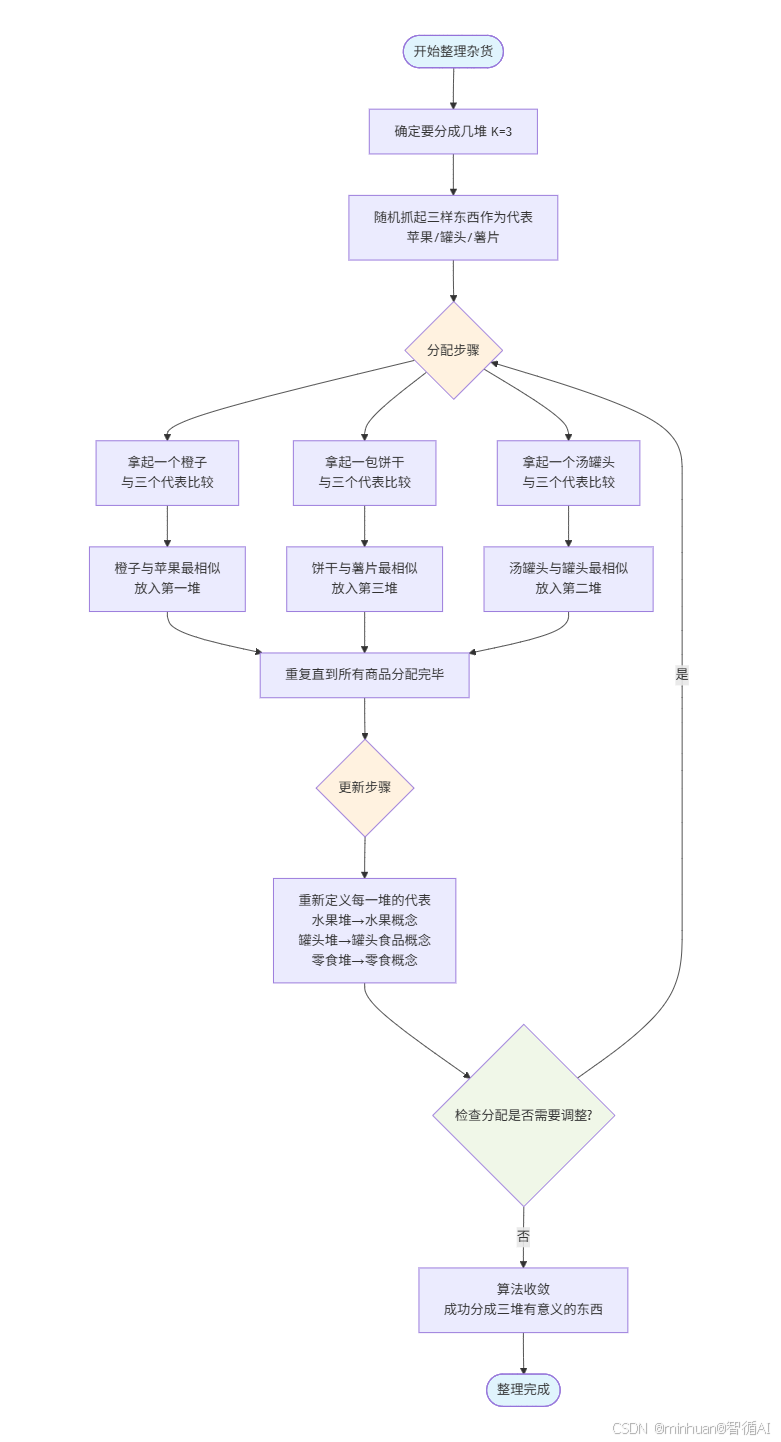
这个流程图直观地展示了 K-Means 算法的核心思想：通过不断迭代"分配-更新"两个步骤，逐步优化分组结果，直到达到稳定状态。

结合例子对Kmeans的流程总结：

开始与初始化：
- 确定要分成几堆（K=3）
- 随机选择三个初始代表（苹果、罐头、薯片）
分配步骤：
- 对于每件商品，与所有代表比较
- 根据相似度分配到最相似的堆中
- 重复直到所有商品分配完毕
更新步骤：
- 基于当前分配，重新定义每堆的代表概念
- 从具体物品升级为抽象概念（如"苹果"→"水果"）
收敛判断：
- 检查分配是否需要调整
- 如果需要调整，回到分配步骤
- 如果不需要，算法收敛，整理完成

通过例子引出来的算法术语：

K-Means 算法术语	通俗例子对应
数据点	杂货商品
簇	商品堆
质心	堆的代表概念
距离度量	相似度比较
分配步骤	将商品分配到最相似的堆
更新步骤	重新定义每堆的代表概念
收敛	所有商品都在最合适的堆中

二、K-Means是什么

1. 基础理解

K-Means 是一种无监督的聚类算法，用于将未标记的数据点自动分组到 K 个簇中。它的核心思想是让同一个簇内的点尽可能相似，不同簇的点尽可能不同。就是我们经常提到的高内聚、低耦合。

“相似”在这里通常由欧氏距离来衡量。一个簇的“中心”由该簇内所有数据点的均值计算得出，这也是算法名称中 “Means” (均值) 的由来。

形象比喻：假设你有一堆散落的糖果，你的目标是把它们按颜色分成 K 个组。

K-Means 的做法是：

随机找 K 个糖果作为初始的“中心糖”。
看每一颗糖离哪个“中心糖”最近，就把它分到哪一组。
重新计算每一组糖的平均位置，更新为新的“中心糖”。
重复步骤 2 和 3，直到“中心糖”的位置不再发生大的变化。

2. 核心概念

簇：一组相似的数据点的集合。
质心：一个簇的中心点，由该簇内所有点的平均值计算得出。
距离度量：通常使用欧几里得距离来衡量点与质心的相似度。距离越小，越相似。

3. 基础流程图

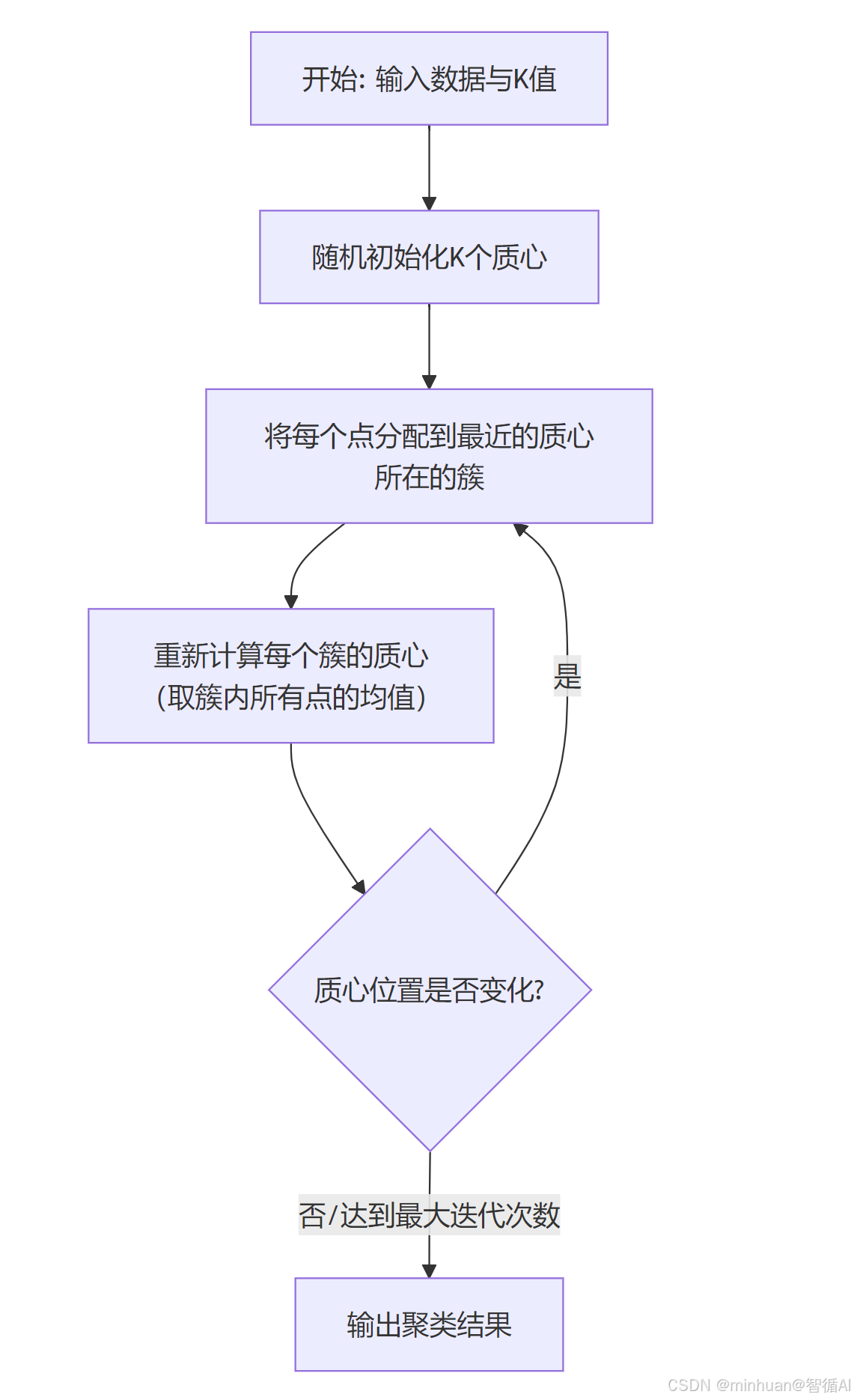
三、K-Means的算法分解

输入：

数据集：包含 n 个数据点，每个数据点是 d 维向量 {x₁, x₂, ..., xₙ}
预设的簇数量：K

输出：

K 个簇：{C₁, C₂, ..., C_K}
每个数据点对应的簇标签

1. 迭代过程

第一步：初始化中心点

从 n 个数据点中随机选择 K 个点作为初始的簇中心，记为 center₁, center₂, ..., center_K。
这是关键一步，不同的初始化方法会极大影响最终结果。

第二步：分配步骤

对于数据集中的每一个数据点 x_i：

计算它到当前所有 K 个簇中心的距离（通常是欧氏距离）
将数据点 x_i 分配给距离最近的那个簇中心所对应的簇

用数学公式表示就是，为每个点找到 j，使得：

距离²(x_i, center_j) ≤ 距离²(x_i, center_k) 对于所有 k

这一步结束后，所有数据点都被分配到了 K 个簇中的某一个。

第三步：更新步骤

对于每一个簇 C_j：

重新计算该簇的中心点
新的中心点是该簇内所有数据点的平均值

计算公式：新中心点 = (1 / 簇中点数) × 所有点的坐标和

第四步：收敛判断

检查簇中心是否发生变化：

如果所有簇中心的变化都非常小（小于某个预设的阈值），则认为算法已经收敛，停止迭代
或者，也可以设置一个最大迭代次数，防止无限循环

如果中心点变化显著，则返回第 2 步继续迭代。

算法关键点说明：

初始化：随机选择初始中心点，不同的选择可能导致不同的结果
距离计算：使用欧氏距离衡量点与中心点的相似度
簇分配：每个点被分配到距离最近的中心点所在的簇
中心点更新：重新计算每个簇的中心点（平均值）
收敛条件：当中心点变化很小时，算法停止

2. 算法示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 生成示例数据
np.random.seed(42)
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.8, random_state=42)# K-Means 算法实现
def k_means(X, k, max_iter=100, tol=1e-4):# 1. 初始化中心点centers = X[np.random.choice(X.shape[0], k, replace=False)]# 存储历史信息用于可视化history = {'centers': [centers.copy()], 'labels': []}for i in range(max_iter):# 2. 分配步骤distances = np.sqrt(((X - centers[:, np.newaxis])**2).sum(axis=2))labels = np.argmin(distances, axis=0)history['labels'].append(labels.copy())# 3. 更新步骤new_centers = np.array([X[labels == j].mean(axis=0) for j in range(k)])# 4. 收敛判断if np.all(np.linalg.norm(new_centers - centers, axis=1) < tol):breakcenters = new_centershistory['centers'].append(centers.copy())return labels, centers, history# 应用 K-Means 算法
k = 4
labels, centers, history = k_means(X, k)# 可视化结果
plt.figure(figsize=(15, 10))# 绘制初始状态
plt.subplot(2, 3, 1)
plt.scatter(X[:, 0], X[:, 1], c='gray', s=30, alpha=0.5)
plt.scatter(history['centers'][0][:, 0], history['centers'][0][:, 1], c='red', s=100, marker='X')
plt.title('初始化: 随机选择中心点')# 绘制迭代过程
for i in range(min(4, len(history['labels']))):plt.subplot(2, 3, i+2)for j in range(k):cluster_points = X[history['labels'][i] == j]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], s=30, alpha=0.5)plt.scatter(history['centers'][i][:, 0], history['centers'][i][:, 1], c='red', s=100, marker='X')plt.scatter(history['centers'][i+1][:, 0], history['centers'][i+1][:, 1], c='green', s=100, marker='X')plt.title(f'迭代 {i+1}: 分配和更新中心点')# 绘制最终结果
plt.subplot(2, 3, 6)
for j in range(k):cluster_points = X[labels == j]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], s=30, alpha=0.5)
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=100, marker='X')
plt.title('最终结果: 算法收敛')plt.tight_layout()
plt.show()# 打印最终中心点位置
print("最终中心点位置:")
for i, center in enumerate(centers):print(f"中心点 {i+1}: ({center[0]:.2f}, {center[1]:.2f})")

3. 输出结果

最终中心点位置:
中心点 1: (4.30, 2.38)
中心点 2: (-6.84, -6.84)
中心点 3: (5.33, 1.48)
中心点 4: (-5.74, 8.10)

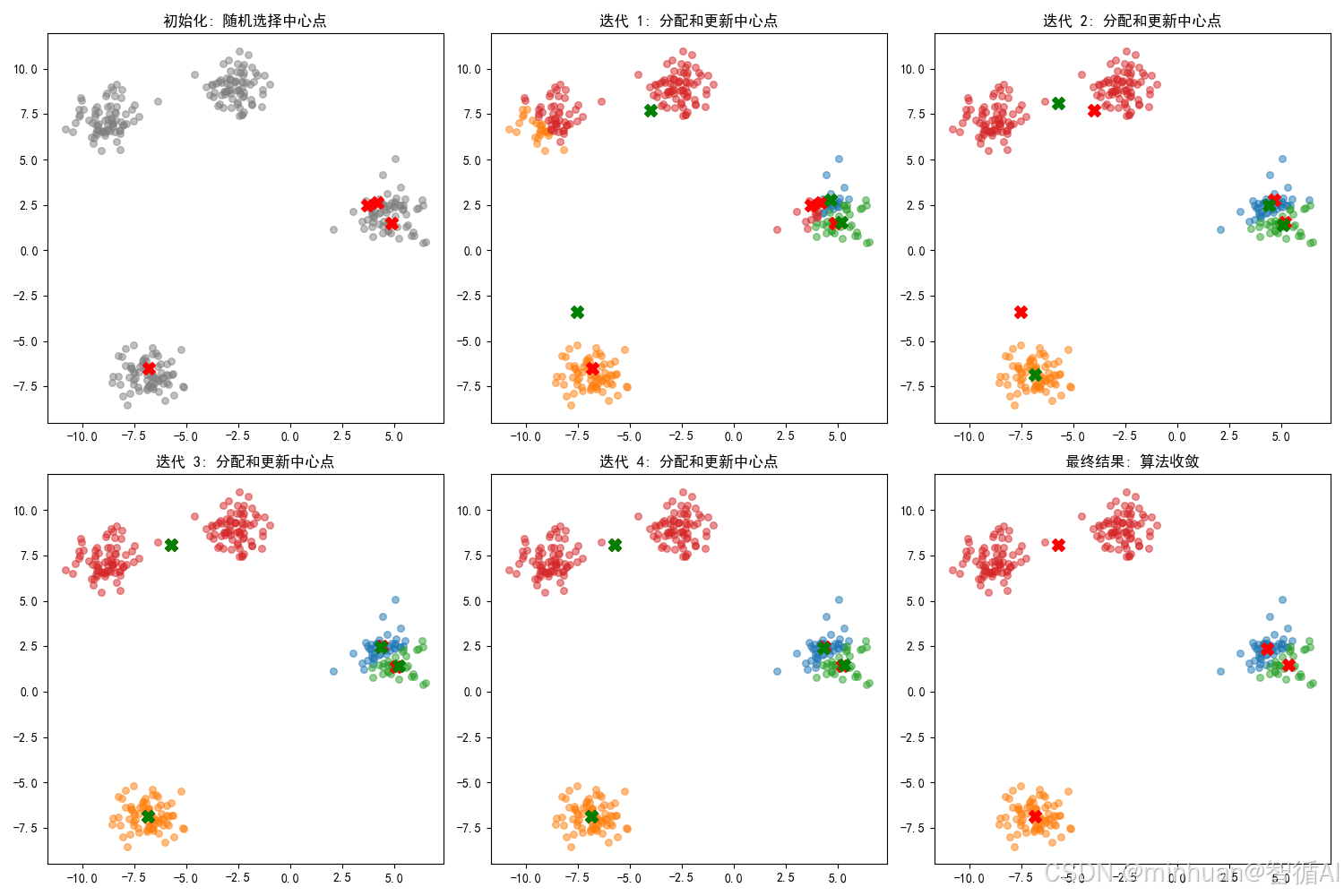
四、K-Means 目标函数与优化方法

1. 目标函数

K-Means 算法的核心是在优化一个目标函数，这个函数称为簇内误差平方和（WCSS），也叫畸变值。目标函数衡量的是所有数据点与其所属簇中心的距离平方之和。公式表示为：

总误差 = 所有簇中 [每个点到其簇中心距离的平方] 的总和

这个值越小，说明聚类效果越好，因为点都紧密地聚集在各自的簇中心周围。

2. 目标函数优化

K-Means 通过两个交替步骤来优化这个目标函数：

分配步骤（固定中心点，优化分组）：
- 保持中心点位置不变
- 将每个点分配到距离最近的中心点所在的簇
- 这一步通过优化点的分组来减小总误差
更新步骤（固定分组，优化中心点）：
- 保持点的分组不变
- 重新计算每个簇的中心点（取簇内所有点的平均值）
- 这一步通过优化中心点位置来减小总误差

算法保证在每次迭代中，总误差值都会减小或保持不变，最终会收敛到一个局部最优解。

3. 算法优化K-Means++

K-Means 算法对初始中心点的选择非常敏感。随机选择初始中心点可能导致：

收敛到局部最优解而非全局最优解
需要更多次迭代才能收敛
不同的运行可能得到不同的结果

解决方案：K-Means++ 初始化方法

K-Means++ 是一种更聪明的初始化方法，它使初始中心点彼此远离，从而提高聚类效果。

K-Means++ 的步骤：

随机选择第一个中心点：从数据点中随机选择第一个中心点
计算最短距离：对于每个数据点，计算它与已选中心点的最短距离（即与最近中心点的距离）
按概率选择下一个中心点：
- 距离越远的点，被选为下一个中心点的可能性越大
- 具体来说，一个点被选中的概率与其到最近中心点距离的平方成正比
重复选择：重复步骤2和3，直到选出K个中心点

K-Means++ 的优势：

初始中心点分布更均匀
减少收敛到局部最优的可能性
通常需要更少的迭代次数
在许多情况下能得到更好的聚类结果

3.1 代码示例

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号# 生成示例数据
np.random.seed(42)
X = np.random.randn(300, 2)# 自己实现 K-Means 算法
def kmeans(X, k, init_method='random', max_iter=100, tol=1e-4):n_samples, n_features = X.shape# 初始化中心点if init_method == 'random':# 随机初始化centers = X[np.random.choice(n_samples, k, replace=False)]elif init_method == 'kmeans++':# K-Means++ 初始化centers = np.zeros((k, n_features))# 第一个中心点随机选择centers[0] = X[np.random.randint(n_samples)]for i in range(1, k):# 计算每个点到最近中心点的距离distances = np.min(np.sqrt(((X - centers[:i, np.newaxis])**2).sum(axis=2)), axis=0)# 按距离平方的概率选择下一个中心点probabilities = distances**2 / np.sum(distances**2)next_center_idx = np.random.choice(n_samples, p=probabilities)centers[i] = X[next_center_idx]# 存储历史信息history = {'centers': [centers.copy()], 'labels': [], 'wcss': []}for iteration in range(max_iter):# 计算每个点到每个中心的距离distances = np.sqrt(((X - centers[:, np.newaxis])**2).sum(axis=2))# 分配步骤：将每个点分配到最近的中心labels = np.argmin(distances, axis=0)history['labels'].append(labels.copy())# 计算 WCSS (Within-Cluster Sum of Squares)wcss = 0for j in range(k):cluster_points = X[labels == j]if len(cluster_points) > 0:wcss += np.sum((cluster_points - centers[j])**2)history['wcss'].append(wcss)# 更新步骤：重新计算中心点new_centers = np.zeros((k, n_features))for j in range(k):cluster_points = X[labels == j]if len(cluster_points) > 0:new_centers[j] = np.mean(cluster_points, axis=0)else:# 如果簇为空，重新初始化该中心点new_centers[j] = X[np.random.randint(n_samples)]# 检查收敛if np.all(np.linalg.norm(new_centers - centers, axis=1) < tol):breakcenters = new_centershistory['centers'].append(centers.copy())return labels, centers, history# 运行随机初始化的 K-Means
labels_random, centers_random, history_random = kmeans(X, k=4, init_method='random')
wcss_random = history_random['wcss'][-1]# 运行 K-Means++ 初始化的 K-Means
labels_plus, centers_plus, history_plus = kmeans(X, k=4, init_method='kmeans++')
wcss_plus = history_plus['wcss'][-1]print(f"随机初始化的误差: {wcss_random:.2f}")
print(f"K-Means++ 初始化的误差: {wcss_plus:.2f}")
print(f"改进: {wcss_random - wcss_plus:.2f} (越小越好)")# 可视化结果
plt.figure(figsize=(15, 5))# 随机初始化的结果
plt.subplot(1, 3, 1)
colors = list(mcolors.TABLEAU_COLORS.values())
for j in range(4):cluster_points = X[labels_random == j]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], c=colors[j], s=30, alpha=0.8)
plt.scatter(centers_random[:, 0], centers_random[:, 1], c='red', marker='X', s=200, edgecolors='black')
plt.title('随机初始化\n误差: {:.2f}'.format(wcss_random))# K-Means++ 初始化的结果
plt.subplot(1, 3, 2)
for j in range(4):cluster_points = X[labels_plus == j]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], c=colors[j], s=30, alpha=0.8)
plt.scatter(centers_plus[:, 0], centers_plus[:, 1], c='red', marker='X', s=200, edgecolors='black')
plt.title('K-Means++ 初始化\n误差: {:.2f}'.format(wcss_plus))# 误差对比
plt.subplot(1, 3, 3)
methods = ['随机初始化', 'K-Means++']
wcss_values = [wcss_random, wcss_plus]
bars = plt.bar(methods, wcss_values, color=['lightblue', 'lightgreen'])
plt.ylabel('WCSS 误差')
plt.title('初始化方法对比')# 在柱状图上添加数值标签
for bar, value in zip(bars, wcss_values):plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 5, f'{value:.2f}', ha='center', va='bottom')plt.tight_layout()
plt.show()# 打印迭代次数和最终中心点
print(f"\n随机初始化迭代次数: {len(history_random['wcss'])}")
print(f"K-Means++ 迭代次数: {len(history_plus['wcss'])}")
print("\n随机初始化最终中心点:")
for i, center in enumerate(centers_random):print(f"中心点 {i+1}: ({center[0]:.2f}, {center[1]:.2f})")
print("\nK-Means++ 最终中心点:")
for i, center in enumerate(centers_plus):print(f"中心点 {i+1}: ({center[0]:.2f}, {center[1]:.2f})")

3.2 输出结果

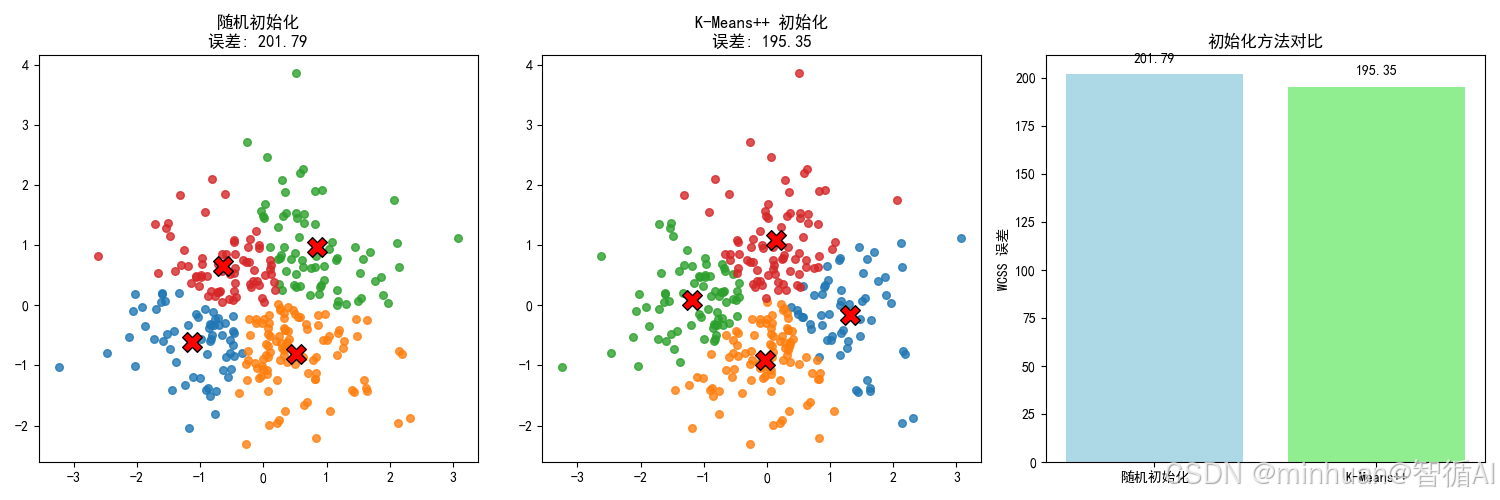
随机初始化的误差: 201.79
K-Means++ 初始化的误差: 195.35
改进: 6.45 (越小越好)

3.3 代码说明

两种初始化方法：
- 随机初始化 (init_method='random')
- K-Means++ 初始化 (init_method='kmeans++')
完整的 K-Means 算法：
- 分配步骤：将点分配到最近的中心
- 更新步骤：重新计算中心点位置
- 收敛判断：当中心点变化很小时停止迭代
WCSS 计算：
- 计算每个簇内点到中心点的距离平方和
- 记录每次迭代的 WCSS 值
可视化：
- 显示两种初始化方法的结果
- 比较它们的 WCSS 值
- 显示迭代次数和最终中心点位置

五、K-Means 与大模型结合

大模型强大但昂贵且缓慢。K-Means 作为一种轻量级、高效的聚类算法，可以与大模型协同工作，主要在以下几个层面发挥作用：

1. 数据预处理与洞察发现

作用：在将大量文本数据送入大模型进行微调（Fine-tuning）或提示学习之前，先用 K-Means 对文本嵌入进行聚类，以理解数据的自然分组和结构。
价值：
- 数据质量检查：快速识别出数据集中的主要话题、异常点或噪声数据。例如，你可能会发现一个簇全是垃圾邮件或无关内容，可以在训练前将其剔除。
- 分层抽样：如果数据集太大，可以对每个簇进行抽样，确保送交给 LLM 的提示（Prompt）或微调数据能均衡地代表所有主要话题，避免模型偏差。
- 理解用户意图：分析客服日志、用户反馈时，可以先聚类，快速了解用户最常抱怨的问题有哪些大类，然后再针对每个簇让 LLM 进行细粒度分析。

2. 提示管理与优化

作用：大模型的应用严重依赖提示（Prompt）。我们可以创建一个“提示库”，并使用 K-Means 对其进行管理和分类。
价值：
- 提示路由：当用户输入一个新查询时，将其转换为嵌入向量，并用训练好的 K-Means 模型快速判断它属于哪个“提示簇”。然后，可以使用该簇对应的、经过优化的最佳提示模板或少量示例来查询大模型，从而显著提升输出质量和稳定性。
- 减少提示工程尝试：通过聚类，你可以发现哪些类型的提示是相似的、效果好坏，从而系统化地管理你的提示策略，而不是盲目尝试。

3. 响应后处理与归纳

作用：大模型可以生成大量内容（如生成了 100 条广告文案），但其中可能存在重复或模式相似的结果。
价值：
- 多样性筛选：将这些生成的文本进行嵌入和聚类，可以从每个簇中挑选一个代表，确保最终输出的多样性和覆盖面，避免给用户提供大量雷同的内容。
- 归纳总结：对于开放域问答，大模型可能会生成很长且角度略有不同的答案。聚类可以帮助识别答案中的不同主题或观点，并在此基础上进行总结。

4. 缓存与成本优化

作用：这是最具实用价值的应用之一，许多用户向大模型提问的问题是相似或重复的。
价值：
- 语义缓存：将用户的问题（Query）通过嵌入模型转换为向量，并用 K-Means 或更精确的向量相似度搜索进行聚类。当一个新问题到来时，系统首先判断它是否与缓存中的某个“问题簇”非常相似。如果是，则直接返回该簇对应的缓存答案，而无需调用昂贵且缓慢的大模型API。这能极大降低成本和延迟。
- 示例：用户问“如何照顾我的宠物狗？”和“养狗需要注意什么？”这两个问题的语义高度相似，可以被归为同一簇，只需计算一次大模型答案。

5. 代码示例：使用 K-Means 对文本进行聚类并分析

以下是一个完整的示例，展示了如何将文本数据通过 Sentence Transformer 转换为嵌入向量，然后用 K-Means 进行聚类，最后使用Qwen模型的API来分析每个簇的主题。

import numpy as np
from sentence_transformers import SentenceTransformer
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import requests
import json
import os
import time# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号# 1. 准备中文新闻标题数据
news_titles = ["股市在经济复苏中创历史新高","新研究显示地中海饮食对心脏健康的益处","地方选举结果公布，现任政党保持席位","科技巨头发布具有先进AI功能的最新智能手机","科学家在亚马逊雨林发现新物种","美联储暗示下季度可能降息","COVID-19疫苗加强针现已向所有成年人开放","足球队在戏剧性决赛后赢得冠军","气候峰会达成碳排放新协议","苹果发布改进相机系统的新iPhone","央行宣布新货币政策以遏制通胀","研究将空气污染与痴呆症风险增加联系起来","市议会批准新公共交通系统预算","三星推出新款可折叠手机参与市场竞争","当地公园发现稀有鸟类，观鸟者蜂拥而至","财政部长评论数字货币未来","癌症治疗突破在临床试验中显示希望","市长候选人承诺解决无家可归危机","谷歌发布搜索算法更新","飓风逼近海岸，居民被敦促撤离"
]# 2. 加载嵌入模型
embedder = SentenceTransformer('paraphrase-multilingual-MiniLM-L12-v2')  # 多语言模型，支持中文# 3. 将文本转换为嵌入向量
corpus_embeddings = embedder.encode(news_titles)# 4. 自己实现 K-Means 算法，避免使用 sklearn
def kmeans_custom(X, n_clusters, max_iter=100, tol=1e-4):# 随机初始化中心点centers = X[np.random.choice(X.shape[0], n_clusters, replace=False)]for _ in range(max_iter):# 计算每个点到每个中心的距离distances = np.sqrt(((X - centers[:, np.newaxis])**2).sum(axis=2))# 分配步骤：将每个点分配到最近的中心labels = np.argmin(distances, axis=0)# 更新步骤：重新计算中心点new_centers = np.array([X[labels == j].mean(axis=0) for j in range(n_clusters)])# 检查收敛if np.all(np.linalg.norm(new_centers - centers, axis=1) < tol):breakcenters = new_centersreturn labels, centers# 使用自定义 K-Means 进行聚类
num_clusters = 5  # 假设有5个主要类别
clusters, centers = kmeans_custom(corpus_embeddings, num_clusters)# 5. 可视化（使用PCA将高维向量降维到2D）
pca = PCA(n_components=2)
reduced_embeddings = pca.fit_transform(corpus_embeddings)# 计算每个簇在2D空间中的中心点
cluster_centers_2d = []
for i in range(num_clusters):cluster_points = reduced_embeddings[clusters == i]if len(cluster_points) > 0:center_2d = np.mean(cluster_points, axis=0)cluster_centers_2d.append(center_2d)else:cluster_centers_2d.append([0, 0])# 6. 打印聚类结果
clustered_titles = {}
for idx, cluster_id in enumerate(clusters):if cluster_id not in clustered_titles:clustered_titles[cluster_id] = []clustered_titles[cluster_id].append(news_titles[idx])print("=== 聚类结果 ===")
for cluster_id, titles in clustered_titles.items():print(f"\n--- 簇 #{cluster_id} (包含 {len(titles)} 个标题) ---")for title in titles:print(f" - {title}")# 7. 使用 Qwen API 总结每个簇的主题
# 设置你的 Qwen API 密钥和端点
QWEN_API_KEY = os.environ.get("DASHSCOPE_API_KEY")
QWEN_API_URL = "https://dashscope.aliyuncs.com/api/v1/services/aigc/text-generation/generation"def summarize_cluster_with_qwen(titles):"""使用 Qwen API 总结一个簇的主题"""# 构建提示词 - 使用字符串连接而不是 f-string 中的反斜杠prompt_lines = ["以下是一组被算法归为一类的新闻标题。","请分析它们的共同主题或话题，并用非常简短的中文标签（3-5个词）进行概括。","","新闻标题："]prompt_lines.extend(titles[:3])  # 只使用前3个标题prompt_lines.extend(["", "共同主题：", ""])prompt = "\n".join(prompt_lines)try:# 构建请求headers = {"Authorization": f"Bearer {QWEN_API_KEY}","Content-Type": "application/json"}payload = {"model": "qwen-max",  # 使用 Qwen 模型"input": {"messages": [{"role": "user","content": prompt}]},"parameters": {"max_tokens": 20,"temperature": 0.1}}# 发送请求response = requests.post(QWEN_API_URL, headers=headers, data=json.dumps(payload))result = response.json()# 提取回复内容if "output" in result and "text" in result["output"]:return result["output"]["text"].strip()else:return f"API 错误: {result.get('message', '未知错误')}"except Exception as e:return f"请求异常: {str(e)}"print("\n=== 正在生成簇主题... ===")
cluster_themes = {}
for cluster_id, titles in clustered_titles.items():print(f"正在分析簇 #{cluster_id}...")theme = summarize_cluster_with_qwen(titles)cluster_themes[cluster_id] = themeprint(f"簇 #{cluster_id} 主题: {theme}")# 添加短暂延迟以避免API限制time.sleep(1)# 8. 创建带有主题标签的可视化
plt.figure(figsize=(14, 10))
scatter = plt.scatter(reduced_embeddings[:, 0], reduced_embeddings[:, 1], c=clusters, cmap='viridis', s=100, alpha=0.7)
plt.colorbar(scatter, label='簇 ID')
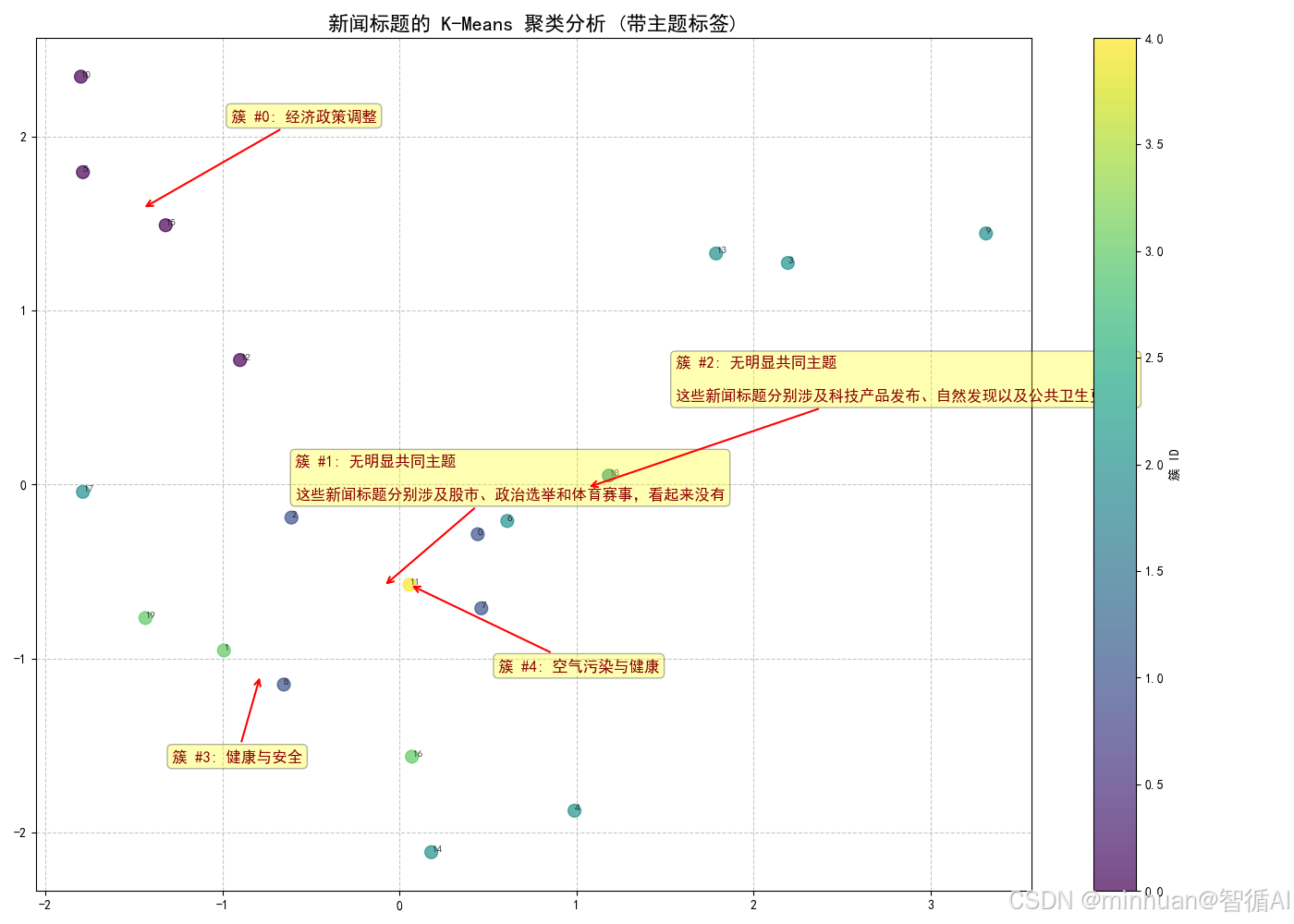
plt.title('新闻标题的 K-Means 聚类分析 (带主题标签)', fontsize=16)# 为每个点添加标题索引
for i, title in enumerate(news_titles):plt.annotate(f"{i}", (reduced_embeddings[i, 0], reduced_embeddings[i, 1]), fontsize=8, alpha=0.7)# 为每个簇添加主题标签
for cluster_id, center_2d in enumerate(cluster_centers_2d):if cluster_id in cluster_themes:theme = cluster_themes[cluster_id]# 计算标签位置（稍微偏移以避免重叠）offset_x = 0.5 if cluster_id % 2 == 0 else -0.5offset_y = 0.5 if cluster_id < 3 else -0.5plt.annotate(f"簇 #{cluster_id}: {theme}",xy=center_2d,xytext=(center_2d[0] + offset_x, center_2d[1] + offset_y),fontsize=12,weight='bold',color='darkred',arrowprops=dict(arrowstyle="->", color='red', lw=1.5),bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.3))plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()# 9. 打印详细的聚类结果
print("\n=== 详细聚类结果 ===")
for cluster_id, titles in clustered_titles.items():theme = cluster_themes.get(cluster_id, "未生成主题")print(f"\n--- 簇 #{cluster_id}: {theme} (包含 {len(titles)} 个标题) ---")for i, title in enumerate(titles):print(f"  {i+1}. {title}")print("\n聚类分析完成!")

输出结果：

=== 聚类结果 ===

--- 簇 #1 (包含 4 个标题) ---
- 股市在经济复苏中创历史新高
- 地方选举结果公布，现任政党保持席位
- 足球队在戏剧性决赛后赢得冠军
- 气候峰会达成碳排放新协议

--- 簇 #3 (包含 3 个标题) ---
- 新研究显示地中海饮食对心脏健康的益处
- 癌症治疗突破在临床试验中显示希望
- 飓风逼近海岸，居民被敦促撤离

--- 簇 #2 (包含 8 个标题) ---
- 科技巨头发布具有先进AI功能的最新智能手机
- 科学家在亚马逊雨林发现新物种
- COVID-19疫苗加强针现已向所有成年人开放
- 苹果发布改进相机系统的新iPhone
- 三星推出新款可折叠手机参与市场竞争
- 当地公园发现稀有鸟类，观鸟者蜂拥而至
- 市长候选人承诺解决无家可归危机
- 谷歌发布搜索算法更新

--- 簇 #0 (包含 4 个标题) ---
- 美联储暗示下季度可能降息
- 央行宣布新货币政策以遏制通胀
- 市议会批准新公共交通系统预算
- 财政部长评论数字货币未来

--- 簇 #4 (包含 1 个标题) ---
- 研究将空气污染与痴呆症风险增加联系起来

=== 正在生成簇主题... ===
正在分析簇 #1...
簇 #1 主题: 无明显共同主题

这些新闻标题分别涉及股市、政治选举和体育赛事，看起来没有
正在分析簇 #3...
簇 #3 主题: 健康与安全
正在分析簇 #2...
簇 #2 主题: 无明显共同主题

这些新闻标题分别涉及科技产品发布、自然发现以及公共卫生更新，
正在分析簇 #0...
簇 #0 主题: 经济政策调整
正在分析簇 #4...
簇 #4 主题: 空气污染与健康

=== 详细聚类结果 ===

--- 簇 #1: 无明显共同主题

这些新闻标题分别涉及股市、政治选举和体育赛事，看起来没有 (包含 4 个标题) ---
1. 股市在经济复苏中创历史新高
2. 地方选举结果公布，现任政党保持席位
3. 足球队在戏剧性决赛后赢得冠军
4. 气候峰会达成碳排放新协议

--- 簇 #3: 健康与安全 (包含 3 个标题) ---
1. 新研究显示地中海饮食对心脏健康的益处
2. 癌症治疗突破在临床试验中显示希望
3. 飓风逼近海岸，居民被敦促撤离

--- 簇 #2: 无明显共同主题

这些新闻标题分别涉及科技产品发布、自然发现以及公共卫生更新， (包含 8 个标题) ---
1. 科技巨头发布具有先进AI功能的最新智能手机
2. 科学家在亚马逊雨林发现新物种
3. COVID-19疫苗加强针现已向所有成年人开放
4. 苹果发布改进相机系统的新iPhone
5. 三星推出新款可折叠手机参与市场竞争
6. 当地公园发现稀有鸟类，观鸟者蜂拥而至
7. 市长候选人承诺解决无家可归危机
8. 谷歌发布搜索算法更新

--- 簇 #0: 经济政策调整 (包含 4 个标题) ---
1. 美联储暗示下季度可能降息
2. 央行宣布新货币政策以遏制通胀
3. 市议会批准新公共交通系统预算
4. 财政部长评论数字货币未来

--- 簇 #4: 空气污染与健康 (包含 1 个标题) ---
1. 研究将空气污染与痴呆症风险增加联系起来

聚类分析完成!