线性代数基础 | 零空间 / 行空间 / 列空间 / 左零空间 / 线性无关 / 齐次 / 非齐次

注：本文为 “线性代数 | 空间 / 齐次性” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未全校去重。
如有内容异常，请看原文。

---

线性、非线性、齐次与非齐次的概念辨析

Mr DaYang 于 2020-05-04 13:03:28 发布

一、概念界定

在数学（尤其是代数、微分方程等领域）中，“线性”“非线性”“齐次”“非齐次”是描述表达式或方程结构的基础术语，其定义需结合数学语境精准理解，避免歧义。

1. 齐次性（Homogeneity）

“齐次性”源于英文“Homogeneity”，其含义为：用于描述一组具有相同“成员（member）或部分（part）”属性的事物。核心内涵是 “属性的一致性”——即一组对象（如多项式的项、方程的两边）在某一特定属性上满足统一标准。在数学中，这一“特定属性”通常指向“次数的统一性”（如多项式各项的次数相同、方程两边的次数相等），是后续判定“齐次多项式”“齐次方程”的核心依据。

例如：若多项式中所有项的“变量指数之和”（即项的次数）完全相同，则该多项式满足“齐次性”，可称为齐次多项式。

2. 线性（Linearity）

从代数本质来看，“线性”的核心是 “一次性与可分离性”，需同时满足两个条件：

• 次数条件：表达式中涉及的“量”（包括标量、矢量、函数、矩阵、导数等）的最高次数为 1；
• 运算条件：“量”之间不包含乘法、除法、指数、对数、三角函数等非线性运算（即“量”需保持“独立分离”状态，无交叉作用）。

从几何意义来看，二维平面中“线性表达式”对应的图像是直线，这也是“线性”名称的直观来源。

3. 齐次（Homogeneous）

在方程或多项式的语境中，“齐次”是“齐次性”的具体体现，核心特征是 “无独立常数项，且各部分次数统一”。

需注意：“无独立常数项”并非单纯指“不含常数”，而是指表达式中不存在“次数为 0 的独立项”（常数项的次数为 0），且所有含变量的项需满足次数一致（后续结合实例详解）。

二、线性与非线性的判定方法

判定的核心是观察表达式中“量”的次数及运算类型，具体可分为以下两类：

（一）线性的判定

满足“线性定义”中“次数为 1”且“无非线性运算”的表达式，即为线性表达式。

1. 代数示例

平面直角坐标系中的直线方程均为线性表达式，例如：
$$y=x+1$$

• 分析：变量 $x$ 的次数为 1，变量 $y$ 的次数为 1；表达式中仅包含加法和乘法（系数与变量的乘法），无乘法（变量间）、指数、对数等运算，符合线性定义。

2. 扩展示例（多变量/函数）

• 多变量线性表达式：$z=2x+3y$（$x,y,z$ 均为一次，无变量间运算）；
• 线性函数关系：$f(x)=3x-2$（函数值与自变量为一次关系，无非线性运算）。

（二）非线性的判定

若表达式不满足“线性”的任一条件（即“量的次数≠1”，或“量参与非线性运算”），则为非线性表达式。

1. 代数示例

• 二次函数（次数≠1）：$$y=x^2+1$$
  分析：变量 $x$ 的次数为 2，不符合“最高次数为 1”的条件，故为非线性；
• 指数函数（非线性运算）：$$y=2^x+3$$
  分析：自变量 $x$ 参与指数运算（非线性运算），即使次数看似“1”，仍为非线性；
• 变量间乘法（非线性运算）：$$z=xy+x$$
  分析：包含变量 $x$ 与 $y$ 的乘法运算（非线性运算），故为非线性。

2. 几何特征

非线性表达式对应的图像通常为曲线（如二次函数对应抛物线、指数函数对应指数曲线），这与线性表达式的“直线”特征形成鲜明对比。

三、齐次与非齐次的判定方法

判定的核心是“多项式次数的统一性”与“是否含独立常数项”，需先明确多项式次数的定义：
多项式中某一项的次数 = 该项所有变量的指数之和；多项式的次数 = 各项次数中的最大值（但齐次多项式需所有项次数相同）。

（一）齐次的判定

“齐次”的核心是“无独立常数项，且各部分次数统一”，具体可分为“齐次多项式”与“齐次方程组”两类：

1. 齐次多项式的判定

满足“所有项的次数完全相同”的多项式，即为齐次多项式（无独立常数项，因常数项次数为 0，无法与其他项的次数统一）。

示例1：二元二次齐次多项式

$$x^2+2xy+3y^2$$
逐项分析次数：

• $x^2$：变量 $x$ 指数为 2，$y$ 指数为 0，次数 = 2 + 0 = 2；
• $2xy$：变量 $x$ 指数为 1，$y$ 指数为 1，次数 = 1 + 1 = 2；
• $3y^2$：变量 $x$ 指数为 0，$y$ 指数为 2，次数 = 0 + 2 = 2；

结论：所有项次数均为 2，无独立常数项，故为齐次多项式（次数为 2 的齐次多项式）。

示例 2：三元五次齐次多项式

$$a^2{b}^3+a^{4}b$$
逐项分析次数（变量为 $a,b$，默认其他字母为常数）：

• $a^2{b}^3$：$a$ 指数为 2，$b$ 指数为 3，次数 = 2 + 3 = 5；
• $a^{4}b$：$a$ 指数为 4，$b$ 指数为 1，次数 = 4 + 1 = 5；

结论：所有项次数均为 5，无独立常数项，故为齐次多项式（次数为 5 的齐次多项式）。

2. 齐次方程组的判定

满足“方程两边各项次数均相等”的方程组，即为齐次方程组。需特别注意：
常数“0”可视为任意次数（因 $0=0\cdot x^0=0\cdot x^1=0\cdot x^2=\dots$），因此“0”能与方程左边任意次数的项匹配，使两边次数统一。

示例：二元二次齐次方程

$$x^2+2xy+3y^2=0$$
分析：

• 左边：齐次多项式，各项次数均为 2；
• 右边：常数“0”，可视为次数 2（与左边次数统一）；
• 无独立常数项（右边“0”非独立常数项，而是次数适配项）；

结论：方程两边次数相等，无独立常数项，故为齐次方程。

（二）非齐次的判定

“非齐次”的核心是“存在独立常数项，或方程两边次数不统一”，最典型的形式是“非齐次方程组”（非齐次多项式因含独立常数项，已不满足“齐次性”，故通常不单独定义“非齐次多项式”，而是通过方程组体现）。

示例：二元二次非齐次方程

$$x^2+2xy+3y^2=1$$
分析：

• 左边：齐次多项式，各项次数均为 2；
• 右边：独立常数项“1”（次数为 0，与左边次数 2 不统一）；
• 存在独立常数项“1”，破坏了“次数统一性”；

结论：方程两边次数不相等，含独立常数项，故为非齐次方程。

扩展说明

非齐次方程的本质是“齐次方程加独立常数项”，例如上述方程可改写为：
$$(x^2+2xy+3y^2)-1=0$$
其中“$x^2+2xy+3y^2$”是齐次部分，“$-1$”是独立常数项（非齐次部分），二者结合构成非齐次方程。

四、明确“线性”与“齐次”的本质区别

对比维度	线性（Linearity）	齐次（Homogeneity）
核心判定标准	次数为 1 + 无非线性运算	无独立常数项 + 各部分次数统一
关注重点	“量”的运算类型与次数限制	“项”的次数统一性与常数项存在性
典型示例	$y=2x+3$（线性，非齐次）	$x^2+xy=0$（齐次，非线性）
关联关系	线性表达式可能是齐次或非齐次	齐次表达式可能是线性或非线性

例如：

• 线性齐次表达式：$y=3x$（次数 1，无非线性运算；无常数项，次数统一）；
• 线性非齐次表达式：$y=3x+2$（次数 1，无非线性运算；含常数项，次数不统一）；
• 非线性齐次表达式：$x^2+y^2=0$（次数 2，非线性；无常数项，次数统一）；
• 非线性非齐次表达式：$x^2+y^2=4$（次数 2，非线性；含常数项，次数不统一）。

---

从线性代数角度图解：通解、特解、非齐次通解、非齐次特解、齐次通解、齐次特解

Uncertainty!! 已于 2022-08-30 22:02:06 修改

声明：本文为笔者研读《Introduction to Linear Algebra》后，对相关内容形成的个人理解。

一、明确齐次与非齐次方程组的概念

齐次与非齐次方程组的定义

二、实例分析：求解线性方程组

为直观阐释上述概念，首先通过一个具体线性方程组的求解过程展开分析，后续将基于该实例进行图解说明。

待求解方程组如下：

（一）构建方程组的增广矩阵

该线性方程组的增广矩阵形式为：

三、非齐次方程组的特解（${\mathbf{x}}_p$，Particular Solution）

非齐次线性方程组的标准形式为 $\mathbf{R}\mathbf{x}=\mathbf{d}$，对应本例的矩阵形式为：

$$\left[\begin{array}{ccc}1& 0& 3\\ 0& 1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}2\\ 1\end{array}\right]$$

1. 特解的求解

选取自由变量 $x_3=0$（自由变量的取值可任意，此处为简化计算选取 $0$），代入方程组可得：

$$\left[\begin{array}{ccc}1& 0& 3\\ 0& 1& -2\end{array}\right]\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]=\left[\begin{array}{c}2\\ 1\end{array}\right]$$

因此，该非齐次方程组的一个特解为：

$${\mathbf{x}}_p=\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]$$

2. 特解的几何意义

从几何角度看，非齐次线性方程组 $\mathbf{R}\mathbf{x}=\mathbf{d}$ 对应三维空间中两个平面的交线，而特解 ${\mathbf{x}}_p$ 是该交线上的任意一个具体点。

四、齐次方程组的基础解系（${\mathbf{x}}_n$，Special Solution，对应零空间解）

齐次线性方程组的标准形式为 $\mathbf{R}\mathbf{x}=0$，对应本例的矩阵形式为：

$$\left[\begin{array}{ccc}1& 0& 3\\ 0& 1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

1. 基础解系的求解

将矩阵形式转化为代数方程组：

$$\{\begin{array}{l}{x}_1+3x_3=0\\ x_2-2x_3=0\end{array}$$

将主元变量（$x_1,x_2$）移至等号左侧，自由变量（$x_3$）移至等号右侧，可得：

$$x_1=-3x_3,x_2=2x_3$$

令自由变量 $x_3=t$（$t$ 为任意常数），则方程组的解可表示为：

$$\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=t\left[\begin{array}{c}-3\\ 2\\ 1\end{array}\right]$$

因此，齐次方程组的基础解系（即零空间中的解向量）为：

$${\mathbf{x}}_n=t\left[\begin{array}{c}-3\\ 2\\ 1\end{array}\right]$$

2. 基础解系的几何意义

齐次线性方程组 $\mathbf{R}\mathbf{x}=0$ 对应三维空间中过原点的两个平面的交线，而基础解系 ${\mathbf{x}}_n$ 是该交线上所有点对应的向量（由自由变量的取值决定向量的缩放）。

五、非齐次方程组的通解（Complete Solution）

1. 通解的构成

线性代数中，非齐次线性方程组 $\mathbf{R}\mathbf{x}=\mathbf{d}$ 的通解由两部分构成：

非齐次方程组的通解 = 齐次方程组的通解 + 非齐次方程组的一个特解

结合本例，齐次方程组的通解为 ${\mathbf{x}}_n=t\left[\begin{array}{c}-3\\ 2\\ 1\end{array}\right]$（$t$ 为任意常数），非齐次方程组的一个特解为 ${\mathbf{x}}_p=\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]$，因此非齐次方程组的通解为：

$${\mathbf{x}}_{\text{通解}}={\mathbf{x}}_p+{\mathbf{x}}_n=\left[\begin{array}{c}2\\ 1\\ 0\end{array}\right]+t\left[\begin{array}{c}-3\\ 2\\ 1\end{array}\right]$$

2. 通解的几何意义

从几何角度看，非齐次方程组的通解对应两个平面交线上的所有点——即通过特解 ${\mathbf{x}}_p$ 对应的点，沿齐次方程组解空间（过原点的直线）方向平移得到的所有点。

六、概念关系图解与证明

为进一步明确通解、特解、非齐次通解、非齐次特解、齐次通解、齐次特解的内在联系，结合本例的几何意义展开如下分析（向量起点均为原点，终点为对应直线上的点）：

（一）非齐次通解与齐次通解、非齐次特解的关系

结论：非齐次通解 = 齐次通解 + 非齐次特解**

几何上，齐次通解对应过原点的直线（红线上所有向量，如蓝色向量），非齐次特解对应非齐次解直线上的一个固定点（如紫色向量）。通过“非齐次特解向量 + 齐次通解中任意向量”的线性组合，可得到非齐次解直线上所有点对应的向量（黑线上所有点），即非齐次通解。

（二）齐次通解与齐次特解的关系

结论 1：齐次通解 = 任意常数 × 齐次特解**

齐次特解是齐次方程组的任意一个非零解（如蓝色向量），通过对该特解进行任意缩放（乘以任意常数），可得到齐次解直线上的所有向量（红线上所有点），即齐次通解。

结论 2：两个齐次特解的差仍为齐次特解**

设 ${\mathbf{y}}_1^{\ast },{\mathbf{y}}_2^{\ast }$ 为齐次方程组 $\mathbf{R}\mathbf{x}=0$ 的两个特解，则：

$$\mathbf{R}({\mathbf{y}}_1^{\ast }-{\mathbf{y}}_2^{\ast })=\mathbf{R}{\mathbf{y}}_1^{\ast }-\mathbf{R}{\mathbf{y}}_2^{\ast }=0-0=0$$

因此，${\mathbf{y}}_1^{\ast }-{\mathbf{y}}_2^{\ast }$ 仍为齐次方程组的特解（如图中白色向量 = 蓝色向量 - 黑色向量）。

推论：若 $\mathbf{y}=a{\mathbf{y}}_1^{\ast }-b{\mathbf{y}}_2^{\ast }$ 为齐次特解，则 $a-b=0$

由于 $\mathbf{y}$ 需满足 $\mathbf{R}\mathbf{y}=0$，代入得：

$$\mathbf{R}(a{\mathbf{y}}_1^{\ast }-b{\mathbf{y}}_2^{\ast })=a\mathbf{R}{\mathbf{y}}_1^{\ast }-b\mathbf{R}{\mathbf{y}}_2^{\ast }=0$$

因 $\mathbf{R}{\mathbf{y}}_1^{\ast }=\mathbf{R}{\mathbf{y}}_2^{\ast }=0$，该式恒成立，但从解的线性相关性可知，只有当系数满足 $a-b=0$ 时，$\mathbf{y}$ 才是齐次解空间中的有效向量（避免重复或冗余）。

（三）非齐次特解与齐次特解的关系

结论 1：非齐次特解 + 确定常数 × 齐次特解 = 另一个非齐次特解**

设 ${\mathbf{x}}_p$ 为非齐次方程组的特解，${\mathbf{x}}_n$ 为齐次方程组的特解，$k$ 为确定常数，则：

$$\mathbf{R}({\mathbf{x}}_p+k{\mathbf{x}}_n)=\mathbf{R}{\mathbf{x}}_p+k\mathbf{R}{\mathbf{x}}_n=\mathbf{d}+k\cdot 0=\mathbf{d}$$

因此，${\mathbf{x}}_p+k{\mathbf{x}}_n$ 仍为非齐次方程组的特解（如图中橙色向量 = 紫色向量 + 固定缩放后的蓝色向量）。

结论 2：两个非齐次特解的差为齐次特解**

设 ${\mathbf{x}}_{p1},{\mathbf{x}}_{p2}$ 为非齐次方程组 $\mathbf{R}\mathbf{x}=\mathbf{d}$ 的两个特解，则：

$$\mathbf{R}({\mathbf{x}}_{p1}-{\mathbf{x}}_{p2})=\mathbf{R}{\mathbf{x}}_{p1}-\mathbf{R}{\mathbf{x}}_{p2}=\mathbf{d}-\mathbf{d}=0$$

因此，${\mathbf{x}}_{p1}-{\mathbf{x}}_{p2}$ 为齐次方程组的特解（如图中粉色向量 = 绿色向量 - 紫色向量，且粉色向量与蓝色向量平行、模长相等）。

（四）非齐次特解的线性组合条件

问题：为何非齐次特解的线性组合系数和需为 1 时，才能得到另一个非齐次特解？**

1. 系数和不为 1 时的情况

设 ${\mathbf{x}}_{p1},{\mathbf{x}}_{p2}$ 为非齐次特解，线性组合为 $\mathbf{y}=a{\mathbf{x}}_{p1}+b{\mathbf{x}}_{p2}$（$a+b\ne 1$），则：

$$\mathbf{R}\mathbf{y}=a\mathbf{R}{\mathbf{x}}_{p1}+b\mathbf{R}{\mathbf{x}}_{p2}=a\mathbf{d}+b\mathbf{d}=(a+b)\mathbf{d}$$

因 $a+b\ne 1$，故 $\mathbf{R}\mathbf{y}=(a+b)\mathbf{d}\ne \mathbf{d}$，即 $\mathbf{y}$ 不满足非齐次方程组，其对应向量的终点不在非齐次解直线上（如图中绿色向量的终点不在黑线上）。

2. 系数和为 1 时的情况

当线性组合系数满足 $a+b=1$ 时，令 $b=1-a$，则：

$$\mathbf{y}=a{\mathbf{x}}_{p1}+(1-a){\mathbf{x}}_{p2}={\mathbf{x}}_{p2}+a({\mathbf{x}}_{p1}-{\mathbf{x}}_{p2})$$

由前文结论可知，${\mathbf{x}}_{p1}-{\mathbf{x}}_{p2}$ 为齐次特解，因此：

$$\mathbf{R}\mathbf{y}=\mathbf{R}{\mathbf{x}}_{p2}+a\mathbf{R}({\mathbf{x}}_{p1}-{\mathbf{x}}_{p2})=\mathbf{d}+a\cdot 0=\mathbf{d}$$

此时 $\mathbf{y}$ 满足非齐次方程组，其对应向量的终点在非齐次解直线上（如图中粉色向量的终点在黑线上）。

综上，若 $\mathbf{y}=a{\mathbf{x}}_{p1}+b{\mathbf{x}}_{p2}$ 为非齐次特解，则必须满足 $a+b=1$。

七、总结

线性方程组的解结构可通过“特解”与“通解”的关系统一表述，.png =700x)结论如下：

1. 齐次方程组的通解由基础解系的所有线性组合构成，几何上对应过原点的直线（或平面、超平面）；

2. 非齐次方程组的通解由“齐次通解 + 非齐次特解”构成，几何上对应齐次解空间沿特解方向平移后的直线（或平面、超平面）；

3. 两个非齐次特解的差为齐次特解，两个齐次特解的线性组合仍为齐次特解；

4. 非齐次特解的线性组合需满足系数和为 1，才能构成新的非齐次特解。

---

再理解：零空间、行空间、列空间、左零空间、基础解系、极大线性无关组、齐次解、非齐次解之间的关系

Uncertainty!! 已于 2024-12-05 17:05:54 修改

此文仅以方阵为例。

1 零空间（Null Space，$N(A)$）

齐次线性方程组

方程组的矩阵表示

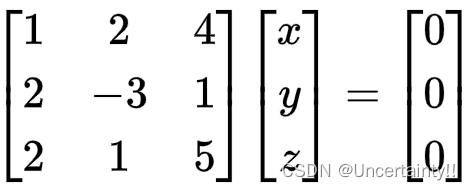
注意此矩阵为 $A$

$$A\vec{x}=\vec{0}$$

从方程组解的角度来看：

上述三个方程分别对应三个平面，三个平面交于一线，这条交线上的每个点 $(x,y,z)$ 代入三个方程都会使得三个方程为 0，即交线上每个点均为三个方程的解，这些点（解）构成了矩阵 $A$ 的零空间。

从线性变换的角度来看：

线性变换前的空间内所有点，在经过矩阵 $A$ 的变换后，在上图交线中的所有点都被压缩到原点。

矩阵 $A$ 的零空间

2 行空间（Row Space，$C(A^T)$）

非齐次线性方程组

方程组的矩阵表示

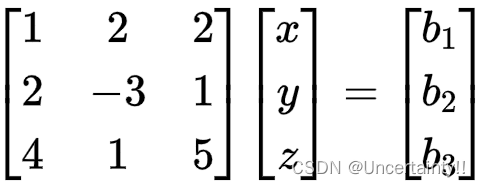
注意此矩阵为 $A^T$

$$A^T\vec{y}=\vec{b}$$

将上式化为矩阵 $A$ 乘以某个向量的形式：

$$\begin{array}{rl}{A}^T\vec{y}& =\vec{b}\\ (A^T\vec{y}{)}^T& ={\vec{b}}^T\\ {\vec{y}}^{T}A& ={\vec{b}}^T\end{array}$$

矩阵左乘向量

下面第一张图来自：矩阵乘法核心思想（2）：行空间

我们观察一下矩阵 $A$ 的行向量与零空间中的向量之间的关系：

矩阵 $A$ 的三个行向量张成行空间，白线为矩阵 $A$ 的零空间，我们发现行空间 $\perp$ 零空间。

3 零空间与行空间

零空间 $\perp$ 行空间。

4 列空间（Column Space，$C(A)$）

非齐次线性方程组

方程组的矩阵表示

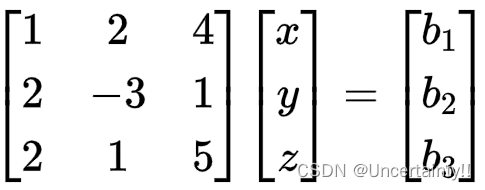
注意此矩阵为 $A$

$$A\vec{x}=\vec{b}$$

矩阵右乘向量

下面第一张图来自：矩阵乘法核心思想（2）：行空间

上图中列空间是由矩阵 $A$ 的三个列向量线性组合张成的空间。

我们将矩阵 $A$ 的三个空间放在一起看看它们之间的关系：

5 左零空间（Left Nullspace，$N(A^T)$）

非齐次线性方程组

方程组的矩阵表示

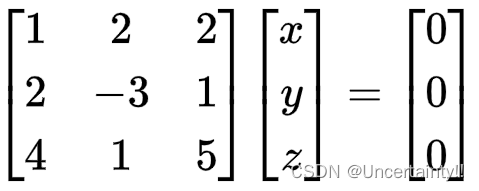
注意此矩阵为 $A^T$

$$A^T\vec{y}=\vec{0}$$

将上式化为矩阵 $A$ 乘以某个向量的形式：

$$\begin{array}{rl}{A}^T\vec{y}& =\vec{0}\\ (A^T\vec{y}{)}^T& ={\vec{0}}^T\\ {\vec{y}}^{T}A& ={\vec{0}}^T\end{array}$$

上述式子中 ${\vec{y}}^{T}A={\vec{0}}^T$，解向量 ${\vec{y}}^T$ 在矩阵 $A$ 的左侧，从这里体现了“左”字。

矩阵 $A$ 的左零空间就是矩阵 $A^T$ 的零空间。

6 列空间与左零空间

左零空间 $\perp$ 列空间

7 各个空间之间的关系

零空间 $\perp$ 行空间

列空间 $\perp$ 左零空间

下面第一张图来自：线性代数“正交”全家桶(2) ：正交子空间

对于任一矩阵 $A_{m\times n}$，都有

$$\text{Row Rank}=\text{Column Rank}=\text{Rank}$$

行空间：$\text{im}(A^T)$

零空间：$\text{ker}(A)$

列空间：$\text{im}(A)$

左零空间：$\text{ker}(A^T)$

行空间和零空间构成 $n$ 维空间。

列空间和左零空间构成 $m$ 维空间。

8 基础解系与极大线性无关组

行空间、零空间、列空间及左零空间均由相应线性方程组的所有解构成。由于每个解均可视为一个点，该点与原点构成向量，因此可以认为线性方程组的解向量构成了上述空间。简而言之，这些空间均为相应线性方程组的解空间。

解向量的极大线性无关组被称为基础解系，该基础解系相当于解空间的基。基础解系能够通过线性组合生成所有解向量，即所有解向量均可由基础解系线性表示。

9 齐次与非齐次方程组的解

零空间和左零空间是齐次方程组的解所构成的空间。

行空间和列空间是非齐次方程组的解所构成的空间。

$$A\vec{x}=\vec{b}$$ 的解集是一个和 $A\vec{x}=\vec{0}$ 的解空间相平行的结构，该结构是 $Ax=0$ 的解空间沿着一个特解方向平移的结果。

下面第一张图来自：矩阵乘法核心思想（3）：零空间

---

via：

• 什么是线性、非线性、齐次、非齐次_齐次和线性怎么理解-CSDN博客
  https://blog.csdn.net/m0_46204224/article/details/105913843

• 从线代角度图解：通解、特解、非齐次通解、非齐次特解、齐次通解、齐次特解_齐次解和特解-CSDN博客
  https://blog.csdn.net/weixin_48524215/article/details/126554508

• 再理解：零空间、行空间、列空间、左零空间、基础解系、极大线性无关组、齐次解、非齐次解之间的关系-CSDN博客
  https://blog.csdn.net/weixin_48524215/article/details/126699137

  • 矩阵乘法核心思想（2）：行空间 - 知乎
    https://zhuanlan.zhihu.com/p/348551903

  • 矩阵乘法核心思想（3）：零空间 - 知乎
    https://zhuanlan.zhihu.com/p/350076095