数据结构【堆(⼆叉树顺序结构)和⼆叉树的链式结构】
Hello大家好! 很高兴与大家见面! 给生活添点快乐,开始今天的编程之路。
我的博客:<但愿.
文章专栏:算法与数据结构
我的专栏:C语言、题目精讲、算法与数据结构、C++
若有问题评论区下讨论,我会及时回答
欢迎大家点赞、关注、收藏分享
目录
1 堆(顺序结构⼆叉树)
1.1定义
1.2分类
1.3 堆的实现
1.4 堆的应⽤
1.4.1 堆排序
1.4.1.1堆排序的实现
1.4.1.2向上调整法与向下调整法哪种更好?
向上调整法思路
向上调整法时间复杂度
向下调整法思路
向下调整法时间复杂度
1.4.2 TOP-K问题【大量数据中排出少量最值数据,例如世界排名】
2 链式结构⼆叉树
2.1链式结构⼆叉树的概念
2.2链式结构⼆叉树相关方法的实现
2.2.1前中后序遍历
2.2.2⼆叉树结点个数
2.2.3⼆叉树叶⼦结点个数
2.2.4 ⼆叉树第k层结点个数
2.2.5⼆叉树的高度/深度
2.2.6 ⼆叉树查找值为x的结点
2.2.7⼆叉树销毁
2.2.8 层序遍历
2.2.9判断是否为完全⼆叉树
1 堆(顺序结构⼆叉树)
1.1定义
堆是⼀种特殊的⼆叉树,只不过其底层结构是顺序结构的数组来存储数据,所以堆不仅具有⼆叉树的特性的同时,还具备其他的特性。
1.2分类
大堆(大根堆):根节点最大的堆
小堆(小根堆):根节点最小的堆
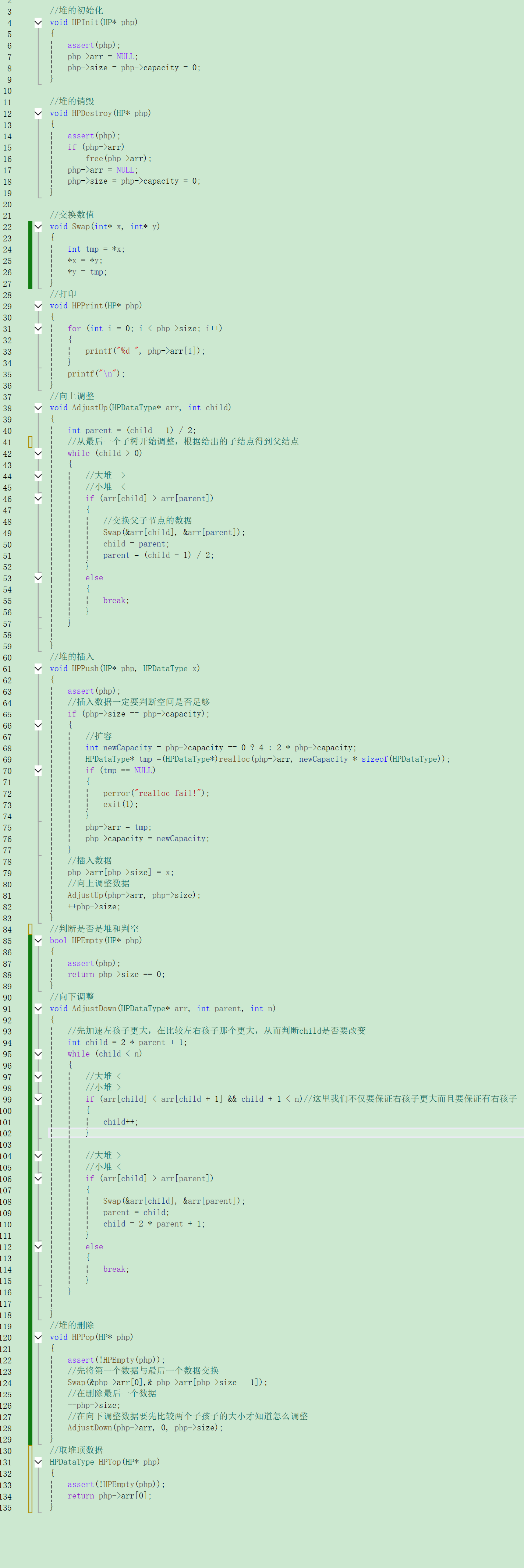
1.3 堆的实现
//堆的结构
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size; //有效数据个数int capacity; //空间大小
}HP;
堆相关方法的实现:
1.4 堆的应⽤
1.4.1 堆排序
1.4.1.1堆排序的实现

1.4.1.2向上调整法与向下调整法哪种更好?
向上调整法思路:
•将堆顶元素与堆中最后⼀个元素进⾏交换•删除堆中最后⼀个元素•将堆顶元素向下调整到满⾜堆特性为⽌
向上调整法时间复杂度(因为完全二叉树和满二叉树在计算时间复杂度时相差不大所以我们将其当成满二叉树来计算)
分析:第1层, 2 0 个结点,需要向上移动0层第2层, 2 1 个结点,需要向上移动1层第3层, 2 2 个结点,需要向上移动2层第4层, 2 3 个结点,需要向上移动3层......第h层, 2 h−1 个结点,需要向上移动h-1层则需要移动结点总的移动步数为:每层结点个数 * 向上调整次数(第⼀层调整次数为0)所以向上调整时间复杂度是:T (h) = 2 1 ∗ 1 + 2 2 ∗ 2 + 2 3 ∗ 3 + .. + 2 h−2 ∗ (h − 2) + 2 h−1 ∗ (h − 1)根据⼆叉树的性质: n = 2 h − 1 和 h = log2 (n + 1)F (n) = (n + 1)(log2 (n + 1) − 2) + 2由此可得:向上调整算法建堆时间复杂度为: O(n ∗ log2 n)
向下调整法思路:
•将堆顶元素与堆中最后⼀个元素进⾏交换•删除堆中最后⼀个元素•将堆顶元素向下调整到满⾜堆特性为⽌
向下调整法时间复杂度
分析:第1层, 2 0 个结点,需要向下移动h-1层第2层, 2 1 个结点,需要向下移动h-2层第3层, 2 2 个结点,需要向下移动h-3层第4层, 2 3 个结点,需要向下移动h-4层......第h-1层, 2 h−2 个结点,需要向下移动1层则需要移动结点总的移动步数为:每层结点个数 * 向下调整次数所以 向下调整法T (h) = 2 0 ∗ (h − 1) + 2 1 ∗ (h − 2) + 2 2 ∗ (h − 3) + 2 3 ∗ (h − 4) + .. + 2 h−3 ∗ 2 + 2 h−2 ∗ 1根据⼆叉树的性质: n = 2 h − 1 和 h = log2 (n + 1)T (n) = n − log2 (n + 1) ≈ n由此可得:向下调整算法建堆时间复杂度为: n所以向下调整法相对更好
1.4.2 TOP-K问题【大量数据中排出少量最值数据,例如世界排名】
下面我们通过一道题目来讲解
总体思路1)⽤数据集合中前K个元素来建堆前k个最⼤的元素,则建⼩堆前k个最⼩的元素,则建⼤堆2)⽤剩余的N-K个元素依次与堆顶元素来⽐较,不满⾜则替换堆顶元素将剩余N-K个元素依次与堆顶元素⽐完之后,堆中剩余的K个元素就是所求的前K个最⼩或者最⼤的元素
代码实现:

2 链式结构⼆叉树
2.1链式结构⼆叉树的概念
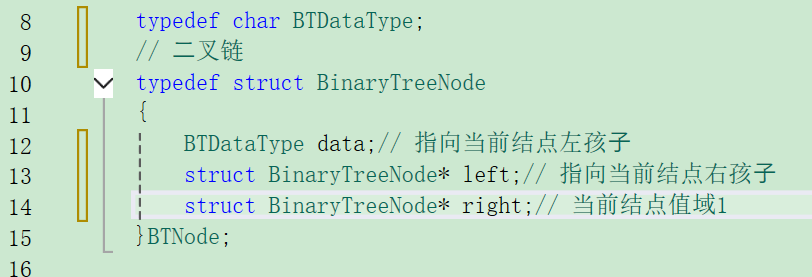
2.2链式结构⼆叉树相关方法的实现
2.2.1前中后序遍历

2.2.2⼆叉树结点个数
2.2.3⼆叉树叶⼦结点个数

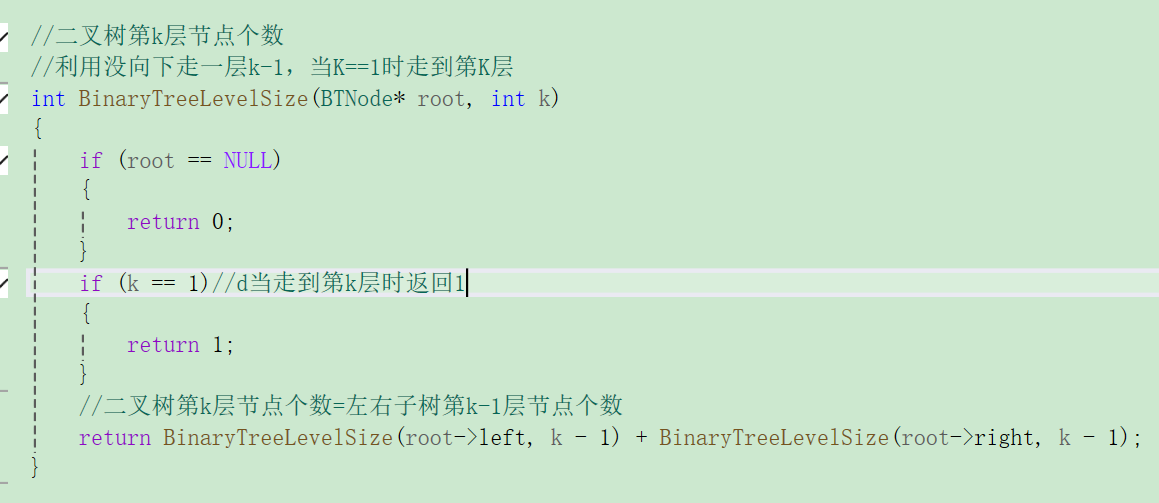
2.2.4 ⼆叉树第k层结点个数
2.2.5⼆叉树的高度/深度

2.2.6 ⼆叉树查找值为x的结点

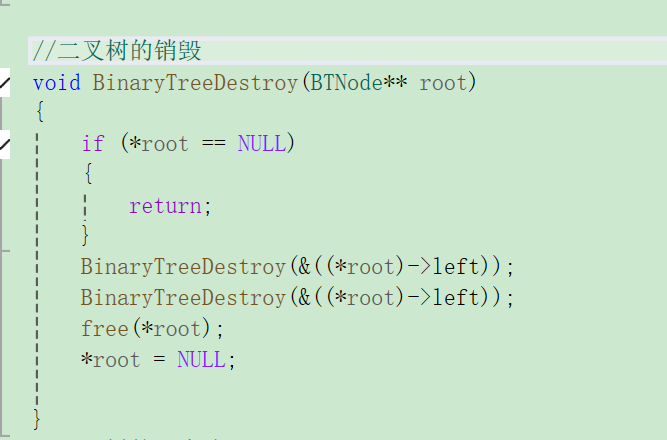
2.2.7⼆叉树销毁
2.2.8 层序遍历
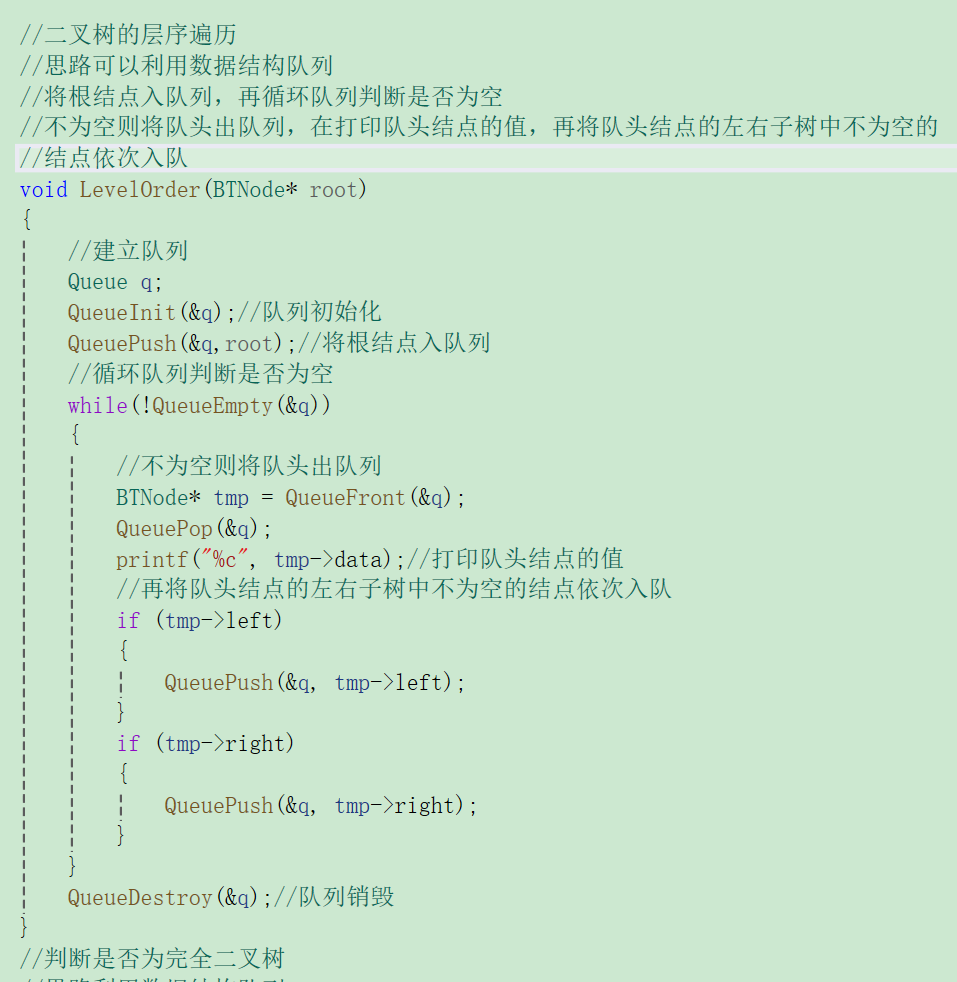
2.2.9判断是否为完全⼆叉树

本篇文章就到此结束,欢迎大家订阅我的专栏,欢迎大家指正,希望有所能帮到读者更好了算法与数据结构相关知识 ,觉得有帮助的还请三联支持一下~后续会不断更新算法与数据结构相关知识,我们下期再见。


