leetcode-hot-100 (多维动态规划）

1、不同路径

题目链接：不同路径
题目描述：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

解答

方法一：动态规划

直接为这个平面图建立一个二维的矩阵 dp ，然后对于左侧和上侧的位置，就只有一种情况。对于其他位置，则 $dp[i][j]=dp[i-1][j]+dp[i][j-1]$

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++)dp[i][0] = 1;for (int i = 0; i < n; i++)dp[0][i] = 1;for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];return dp[m - 1][n - 1];}
};

方法二：滚动数组优化

此外，由于 f(i,j) 仅与第 i 行和第 i − 1 行的状态有关，因此我们可以使用滚动数组代替代码中的二维数组，使空间复杂度降低为 O(n)。

class Solution {
public:int uniquePaths(int m, int n) {vector<int> f(n, 1);for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)f[j] += f[j - 1];return f[n - 1];}
};

方法三：组合数学

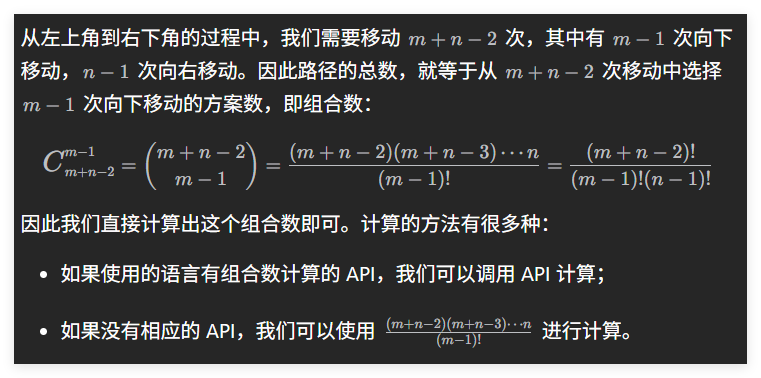
class Solution {
public:int uniquePaths(int m, int n) {long long ans = 1;for (int x = n, y = 1; y < m; ++x, ++y) {ans = ans * x / y;}return ans;}
};作者：力扣官方题解
链接：https://leetcode.cn/problems/unique-paths/solutions/514311/bu-tong-lu-jing-by-leetcode-solution-hzjf/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution
{
private:int combination(int n, int k){assert(k <= n); // 确保 k 不大于 nif (k > n - k)k = n - k; // 优化计算过程,选择小一点的数字进行组合计算比较的好long long int result = 1;for (int i = 1; i <= k; ++i){result *= n - (k - i);result /= i;}return result;}public:int uniquePaths(int m, int n){return combination( m + n - 2 , m - 1);}
};

2、最小路径和

题目链接：最小路径和
题目描述：
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

解答

方法一：动态规划

由于这道题目只能向下和向右走，因此第一行和第一列的路径和是可以直接确定的，可以作为动态规划的边界条件，后面对于剩下的区域，可以使用下面的公式进行求解：
$$grid[i][j]+=min(grid[i-1][j],grid[i][j-1])$$

class Solution
{
public:int minPathSum(vector<vector<int>> &grid){int m = grid.size();int n = grid[0].size();for (int i = 1; i < m; i++)grid[i][0] += grid[i - 1][0];for (int i = 1; i < n; i++)grid[0][i] += grid[0][i - 1];for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)grid[i][j] += min(grid[i - 1][j], grid[i][j - 1]);return grid[m - 1][n - 1];}
};

3、最长回文子串

题目链接：最长回文子串
题目描述：给你一个字符串 s，找到 s 中最长的 回文子串。

解答

方法一：动态规划

对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串 “ababa”，如果我们已经知道 “bab” 是回文串，那么 “ababa” 一定是回文串，这是因为它的首尾两个字母都是 “a”。

根据这样的思路，我们就可以用动态规划的方法解决本题。我们用 $P(i,j)$ 表示字符串 $s$ 的第 $i$ 到 $j$ 个字母组成的串（下文表示成 $s[i:j]$）是否为回文串：

$$P(i,j)=\{\begin{array}{ll}\text{true},& \text{如果子串 }{S}_i\dots S_j\text{ 是回文串}\\ \text{false},& \text{其它情况}\end{array}$$

这里的「其它情况」包含两种可能性：

• $s[i,j]$ 本身不是一个回文串；
• $i>j$，此时 $s[i,j]$ 本身不合法。

那么我们就可以写出动态规划的状态转移方程：

$$P(i,j)=P(i+1,j-1)\wedge (S_i==S_j)$$

也就是说，只有 $s[i+1:j-1]$ 是回文串，并且 $s$ 的第 $i$ 和 $j$ 个字母相同时，$s[i:j]$ 才会是回文串。

上文的所有讨论是建立在子串长度大于 2 的前提之上的，我们还需要考虑动态规划中的边界条件，即子串的长度为 1 或 2。对于长度为 1 的子串，它显然是个回文串；对于长度为 2 的子串，只要它的两个字母相同，它就是一个回文串。因此我们就可以写出动态规划的边界条件：

$$\{\begin{array}{l}P(i,i)=\text{true}\\ P(i,i+1)=(S_i==S_{i+1})\end{array}$$

根据这个思路，我们就可以完成动态规划了，最终的答案即为所有 $P(i,j)=\text{true}$ 中 $j-i+1$（即子串长度）的最大值。注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

class Solution {
public:string longestPalindrome(string s) {int n = s.size();if (n < 2)return s;int maxLen = 1;int begin = 0;vector<vector<int>> dp(n, vector<int>(n));for (int i = 0; i < n; i++)dp[i][i] = true;// 枚举长度for (int L = 2; L <= n; L++) {for (int i = 0; i < n; i++) {int j = L + i - 1;// 剪枝if (j >= n)break;if (s[i] != s[j])dp[i][j] = false;else {if (j - i < 3)dp[i][j] = true;elsedp[i][j] = dp[i + 1][j - 1];}// 给 maxLen 赋值为最大值if (dp[i][j] && j - i + 1 > maxLen) {maxLen = j - i + 1;begin = i;}}}return s.substr(begin, maxLen);}
};

方法二：中心扩展算法

仔细观察一下方法一中的状态转移方程：

$\{\begin{array}{ll}P(i,i)& =\text{true}\\ P(i,i+1)& =(S_i==S_{i+1})\\ P(i,j)& =P(i+1,j-1)\wedge (S_i==S_j)\end{array}$

找出其中的状态转移链:

$P(i,j)\leftarrow P(i+1,j-1)\leftarrow P(i+2,j-2)\leftarrow \cdots \leftarrow \text{某一边界情况}$

可以发现，所有的状态在转移的时候的可能性都是唯一的。也就是说，可以从每一种边界情况开始「扩展」，也可以得出所有的状态对应的答案。

边界情况即为子串长度为 1 或 2 的情况。我们枚举每一种边界情况，并从对应的子串开始不断地向两边扩展。如果两边的字母相同，我们就可以继续扩展，例如从 $P(i+1,j-1)$ 扩展到 $P(i,j)$；如果两边的字母不同，我们就可以停止扩展，因为在这之后的子串都不能是回文串了。

方法二的本质即为：枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

class Solution {
public:pair<int, int> expandAroundCenter(const string& s, int left, int right) {while (left >= 0 && right < s.size() && s[left] == s[right]) {--left;++right;}return {left + 1, right - 1};}string longestPalindrome(string s) {int start = 0, end = 0;for (int i = 0; i < s.size(); i++) {auto [left1, right1] = expandAroundCenter(s, i, i);auto [left2, right2] = expandAroundCenter(s, i, i + 1);if (right1 - left1 > end - start) {start = left1;end = right1;}if (right2 - left2 > end - start) {start = left2;end = right2;}}return s.substr(start, end - start + 1);}
};

方法三：Manacher 算法

这种方法我没咋理解，这里贴上管解答：方法三：Manacher
有时间再看

class Solution {
public:int expand(const string& s, int left, int right) {while (left >= 0 && right < s.size() && s[left] == s[right]) {--left;++right;}return (right - left - 2) / 2;}string longestPalindrome(string s) {int start = 0, end = -1;string t = "#";for (char c : s) {t += c;t += '#';}t += '#';s = t;vector<int> arm_len;int right = -1, j = -1;for (int i = 0; i < s.size(); ++i) {int cur_arm_len;if (right >= i) {int i_sym = j * 2 - i;int min_arm_len = min(arm_len[i_sym], right - i);cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);} else {cur_arm_len = expand(s, i, i);}arm_len.push_back(cur_arm_len);if (i + cur_arm_len > right) {j = i;right = i + cur_arm_len;}if (cur_arm_len * 2 + 1 > end - start) {start = i - cur_arm_len;end = i + cur_arm_len;}}string ans;for (int i = start; i <= end; ++i) {if (s[i] != '#') {ans += s[i];}}return ans;}
};

4、最长公共子序列

题目链接：最长公共子序列
题目描述：
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

解答

方法一：动态规划

class Solution {
public:/*** 计算两个字符串的最长公共子序列（Longest Common Subsequence, LCS）的长度。* 使用动态规划方法，时间复杂度 O(m * n)，空间复杂度 O(m * n)。* * @param text1 第一个字符串* @param text2 第二个字符串* @return 最长公共子序列的长度*/int longestCommonSubsequence(string text1, string text2) {int m = text1.length(); // 获取 text1 的长度int n = text2.length(); // 获取 text2 的长度// 如果任意一个字符串为空，则公共子序列长度为 0if (m == 0 || n == 0)return 0;// 创建一个二维动态规划数组 dp，大小为 (m+1) x (n+1)// dp[i][j] 表示 text1 的前 i 个字符 和 text2 的前 j 个字符 的最长公共子序列长度// 初始化为 0，因为前 0 行和前 0 列对应空字符串的情况vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));// 填充 dp 表格// i 从 1 到 m，表示遍历 text1 的每一个字符（1-indexed）// j 从 1 到 n，表示遍历 text2 的每一个字符（1-indexed）for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 注意：字符串索引是 0-based，所以 text1[i-1] 对应第 i 个字符if (text1[i - 1] == text2[j - 1]) {// 当前字符匹配// 则 LCS 长度 = 前一个位置（i-1, j-1）的 LCS 长度 + 1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 当前字符不匹配// 则 LCS 长度 = 不包含 text1[i-1] 或 不包含 text2[j-1] 的两种情况中的最大值// 即：max( dp[i-1][j], dp[i][j-1] )dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// dp[m][n] 存储的是整个 text1 和 text2 的最长公共子序列长度return dp[m][n];}
};

方法二：一维数组 + 滚动更新

解题思路详解（空间优化的动态规划）

1. 传统二维 DP 回顾

在标准的 LCS 解法中，我们使用一个二维数组 dp[i][j] 表示：

text1[0..i-1] 和 text2[0..j-1] 的最长公共子序列长度。

状态转移方程：

if (text1[i-1] == text2[j-1])dp[i][j] = dp[i-1][j-1] + 1;
elsedp[i][j] = max(dp[i-1][j], dp[i][j-1]);

2. 空间优化思想

我们发现：

• 每一行 dp[i][*] 只依赖于上一行 dp[i-1][*]。
• 因此可以用一维数组滚动更新，从前往后或从后往前更新。

但注意：如果从左往右更新，会覆盖上一行的数据，所以必须巧妙设计更新顺序。

---

3. 本解法的巧妙之处

这个方法不是简单地滚动数组，而是利用了 “maxLen” 变量来模拟 dp[i-1][j-1] 的作用。

• maxLen：表示在当前 i（text1 的当前字符）下，已经处理过的 j 位置中，能形成的最大 LCS 长度。
• 当 text1[i] == text2[j] 时，我们不能直接用 dp[j]，因为那是“上一行”的值。
• 但我们知道：如果匹配成功，应该用“左上角”的值 + 1，而 maxLen 实际上就是 dp[i-1][0..j-1] 的最大值，近似于“左上角”状态。

⚠️ 注意：这里的 maxLen 并不是严格意义上的 dp[i-1][j-1]，但由于我们是从左到右遍历，maxLen 是到 j 为止最大的 dp[j]（即上一行的值），所以当匹配发生时，maxLen 实际上代表了 在 j 之前能形成的最长公共子序列长度，这正是我们想要的。

---

📌 举个例子说明

text1 = "abc"
text2 = "ac"

初始：dp = [0, 0]

• i=0 (char ‘a’)：

  • j=0: ‘a’==‘a’ → dp[0] = maxLen(0) + 1 = 1, maxLen = max(0, 0) = 0 → 然后 maxLen = 1
  • j=1: ‘a’!=‘c’ → 不更新 dp，maxLen = max(1, dp[1]=0)=1
  • 结果：dp = [1, 0]

• i=1 (char ‘b’)：

  • j=0: ‘b’!=‘a’ → 不更新，maxLen = max(0, dp[0]=1) = 1
  • j=1: ‘b’!=‘c’ → 不更新，maxLen = max(1, dp[1]=0) = 1
  • 结果：dp = [1, 0]（未变）

• i=2 (char ‘c’)：

  • j=0: ‘c’!=‘a’ → maxLen = max(0, dp[0]=1) = 1
  • j=1: ‘c’==‘c’ → dp[1] = maxLen(1) + 1 = 2
  • 结果：dp = [1, 2]

最终：max_element(dp) = 2 ✅

---

✅ 复杂度分析

• 时间复杂度：O(m × n)，其中 m = text1.size(), n = text2.size()，两层循环。
• 空间复杂度：O(n)，只用了一个长度为 text2.size() 的一维数组。

---

🔁 与传统二维 DP 的对比

方法	时间复杂度	空间复杂度	优点	缺点
二维 DP	O(mn)	O(mn)	易理解，可回溯路径	空间开销大
一维滚动数组	O(mn)	O(n)	空间优化	逻辑稍复杂
本解法（maxLen 技巧）	O(mn)	O(n)	空间最优，代码简洁	理解难度较高，不易回溯路径

class Solution {
public:/*** 计算两个字符串的最长公共子序列（LCS）的长度。* 使用空间优化的一维动态规划方法，空间复杂度 O(n)，时间复杂度 O(m * n)** @param text1 第一个字符串* @param text2 第二个字符串* @return 最长公共子序列的长度*/int longestCommonSubsequence(string text1, string text2) {// dp[j] 表示：当前遍历到 text1 的某个字符时，// text1 的前缀 与 text2 的前 j+1 个字符构成的 LCS 长度// 即：dp[j] 对应的是 text2[0..j] 的匹配情况vector<int> dp(text2.size(), 0);// 外层循环：遍历 text1 的每一个字符for (int i = 0; i < text1.size(); i++) {int maxLen = 0; // 记录在当前行（即处理 text1[i]）时，已经出现的最大 LCS 长度// 内层循环：遍历 text2 的每一个字符for (int j = 0; j < text2.size(); ++j) {// newLen 是更新前的 dp[j] 和 maxLen 中的较大值// 目的是保留“到目前为止”在当前行中能形成的最长 LCSint newLen = max(maxLen, dp[j]);// 关键判断：如果 text1[i] == text2[j]，说明字符匹配if (text1[i] == text2[j]) {// 此时，新的 LCS 长度 = 当前位置之前（j 之前）的最大 LCS 长度 + 1// 注意：maxLen 是 j 之前的 dp 值中的最大值，相当于“左上角”的状态（类似二维 DP 中的 dp[i-1][j-1]）dp[j] = maxLen + 1;}// 更新 maxLen 为包含当前 j 位置的新最大值maxLen = newLen;}}// 遍历结束后，dp 数组中最大的值就是整个 LCS 的长度return *max_element(dp.cbegin(), dp.cend());}
};

5、编辑距离

题目链接：编辑距离
题目描述：给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

解答

这是一道难题，管解我没咋看，写一下我的思路吧：

class Solution {
public:int minDistance(string word1, string word2) {// 分别记录两单词的长度int len_x = word1.length();int len_y = word2.length();// 动态规划数组vector<vector<int>> dp(len_x + 1, vector<int>(len_y + 1, 0));// 边界条件处理for (int i = 0; i <= len_x; i++)dp[i][0] = i;for (int j = 1; j <= len_y; j++)dp[0][j] = j;for (int i = 1; i <= len_x; i++) {for (int j = 1; j <= len_y; j++) {// 这个位置无需更新if (word1[i - 1] == word2[j - 1])dp[i][j] = dp[i - 1][j - 1];// 否则找到最小的更新步骤elsedp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1 ;}}return dp[len_x][len_y];}
};