黑盒测试:测试用例设计之边界值设计方法(边界值分析法)(上点、离点、内点)健壮性测试、单缺陷假设理论
文章目录
- 测试用例设计之边界值设计方法
- 一、边界值分析法简介
- 二、边界值类型
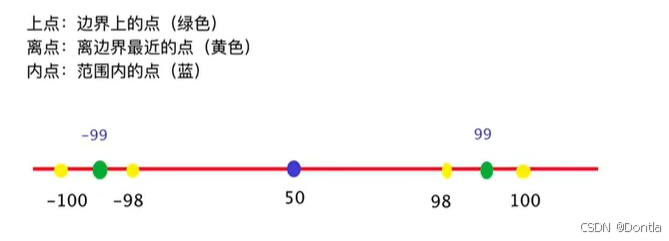
- 1. **上点**:边界上的点
- 2. **离点**:离上点最近的点(边界值±1)
- 3. **内点**:在域的范围内的点
- 三、边界条件分析
- 1. **输入条件明确了一个值的取值范围**
- 2. **输入条件明确了一个值的个数**
- 3. **输入或输出是一个有序集合**
- 四、边界值分析原则
- 考虑因素
- - 有效范围的边界点(最小个数、最大个数)
- - 边界附近的异常点(小于最小有效值、大于最大有效值)
- 1. **对于取值范围**:
- 2. **对于值的个数**:
- 3. **对于有序集合**:
- 五、边界值测试用例设计示例
- 示例1:QQ号长度(5-13位,闭区间)
- 示例2:微信红包金额(0.01-200元,闭区间)
- 示例3:ATM机取款金额(100-5000元,闭区间)
- 六、边界值分析的扩展:健壮性测试
- 七、边界值分析法的优势
- 八、边界值分析与可靠性理论
测试用例设计之边界值设计方法
一、边界值分析法简介
边界值分析法是对输入或输出的边界值进行测试的一种黑盒测试方法。根据测试经验,大量的错误是发生在输入或输出的边界上,而不是发生在输入输出范围的内部。因此,针对各种边界情况设计测试用例可以查出更多的错误。
二、边界值类型
在边界值分析中,通常关注以下几种边界点:
1. 上点:边界上的点
2. 离点:离上点最近的点(边界值±1)
3. 内点:在域的范围内的点
三、边界条件分析
边界值分析主要针对以下三种输入条件:
1. 输入条件明确了一个值的取值范围
- 例如:QQ号5-13位、微信红包金额0.01-200元
2. 输入条件明确了一个值的个数
- 例如:ATM机取款金额100-5000元
3. 输入或输出是一个有序集合
- 例如:列表中的第一个和最后一个元素
四、边界值分析原则
考虑因素
- 有效范围的边界点(最小个数、最大个数)
- 边界附近的异常点(小于最小有效值、大于最大有效值)
1. 对于取值范围:
- 最小值
- 最大值
- 略小于最小值
- 略大于最大值
- 范围内的典型值
2. 对于值的个数:
- 最大个数
- 最小个数
- 比最小个数少1
- 比最大个数多1
3. 对于有序集合:
- 集合的第一个元素
- 集合的最后一个元素
五、边界值测试用例设计示例
示例1:QQ号长度(5-13位,闭区间)
- 上点:5,13
- 离点:4,14
- 内点:8(6,7,8,9,10,11,12)
- 测试用例:5(最小值),13(最大值),4(小于最小值),14(大于最大值),8(范围值)
示例2:微信红包金额(0.01-200元,闭区间)
- 最小值:0.01
- 最大值:200
- 小于最小值:0.00
- 大于最大值:200.01
- 范围值:100(0.02-199.99)
示例3:ATM机取款金额(100-5000元,闭区间)
- 最小金额:100
- 最大金额:5000
- 小于最小金额:99
- 大于最大金额:5001
- 范围值:200
六、边界值分析的扩展:健壮性测试
健壮性边界值分析是在一般边界值分析基础上,增加了:
- 略小于最小值(min-)
- 略大于最大值(max+)
这样,对于n个变量的函数,健壮性测试会产生6n+1个测试用例,比一般边界值分析(4n+1个)更全面。
边界值分析法的测试用例数量:一般边界值分析(4n+1)和健壮性测试(6n+1)计算依据
七、边界值分析法的优势
边界值分析法是发现bug能力最强的一种测试方法,因为它针对的是最容易出错的边界情况。在实际测试工作中,边界值分析通常与等价类划分法配合使用,能更有效地发现软件缺陷。
八、边界值分析与可靠性理论
边界值分析基于"单缺陷假设"理论,即失效极少是由两个(或多个)缺陷的同时发生引起的。在极端情况下,如果拒绝"单缺陷假设",可以采用最坏情况测试,但这种方法代价较高,通常只用于物理变量具有大量交互作用,或者函数失效代价极高的情况。
通过合理应用边界值分析法,可以显著提高测试效率,发现更多潜在的软件缺陷。
