专题二 二叉树中的深度优先搜索

例题1.计算布尔二叉树的值

1.题目

题目链接：计算布尔二叉树的值
给你一棵 完整二叉树 的根，这棵树有以下特征：

叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。
非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。
计算 一个节点的值方式如下：

如果节点是个叶子节点，那么节点的 值 为它本身，即 True 或者 False 。
否则，计算 两个孩子的节点值，然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。

完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。

叶子节点 是没有孩子的节点。

示例 1：

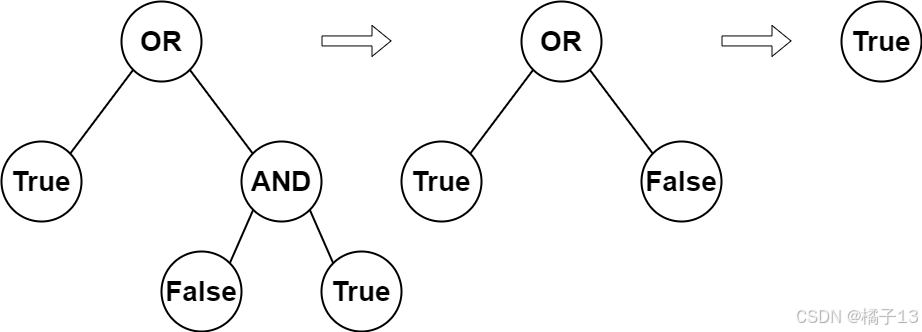
输入：root = [2,1,3,null,null,0,1] 输出：true 解释：上图展示了计算过程。 AND 与运算节点的值为
False AND True = False 。 OR 运算节点的值为 True OR False = True 。 根节点的值为 True
，所以我们返回 true 。 示例 2： 输入：root = [0] 输出：false 解释：根节点是叶子节点，且值为
false，所以我们返回 false 。

提示：
树中节点数目在 [1, 1000] 之间。
0 <= Node.val <= 3
每个节点的孩子数为 0 或 2 。
叶子节点的值为 0 或 1 。
非叶子节点的值为 2 或 3 。

2.算法原理

1.重复子问题——>函数头设计

bool dfs(TreeNode* root)

2.只关心一个子问题在做什么——>函数体的设计

bool left = dfs(root->left);
bool right = dfs(root->right);
return left||right or left&&right

3.递归的退出

root->val == 0  return false;
root->val == 1  return true;

3.编写代码

class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr) return root->val == 0? false : true;bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2? left|right : left&right;}
};

例题2.求根节点到叶节点数字之和

1.题目

题目链接：求根节点到叶节点数字之和
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

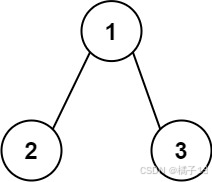
输入：root = [1,2,3] 输出：25 解释： 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字
13 因此，数字总和 = 12 + 13 = 25 示例 2：

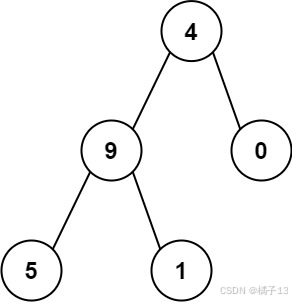
输入：root = [4,9,0,5,1] 输出：1026 解释： 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径
4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此，数字总和 = 495 + 491 + 40 =
1026

提示：
树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

2.算法原理

1.重复子问题——>函数头设计
int dfs(root, presum)
2.只关心一个子问题在做什么——>函数体的设计

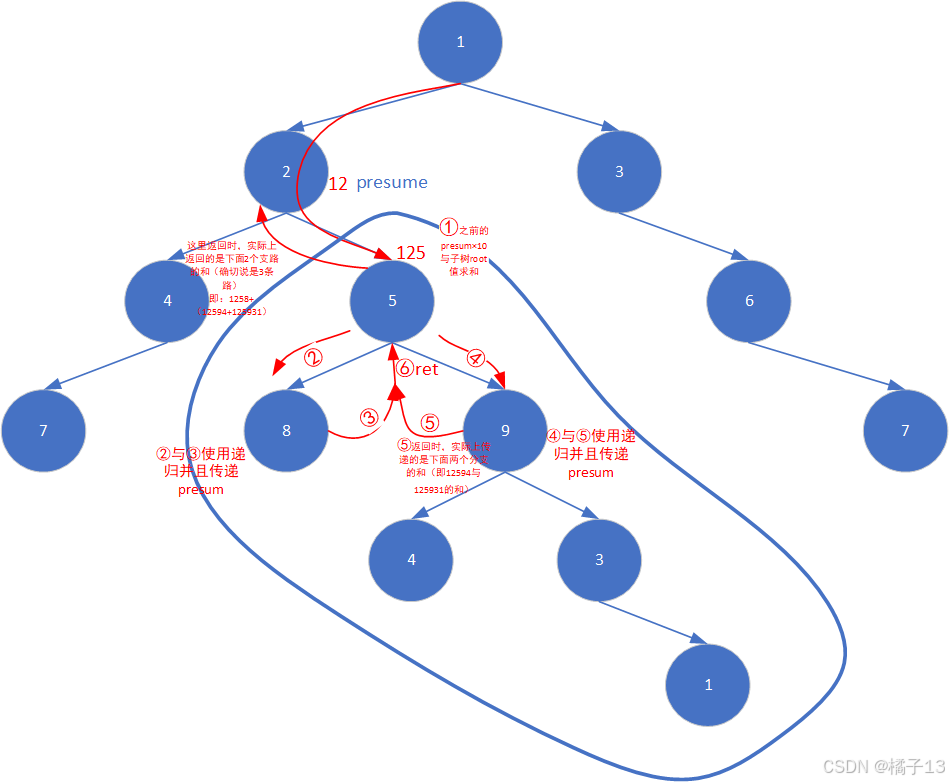
函数体步骤如上图中1,2,3,4,5,6
3.递归的退出
遇到叶子节点时返回,注意这一步要插入在1步骤后面，因为确保到达叶子节点后，要把叶子节点的值算上，所以先执行1后进行递归退出的判断。

3.编写代码

class Solution {
public:int sumNumbers(TreeNode* root) {return dfs(root, 0);}int dfs(TreeNode* root, int presum){presum = presum*10 + root->val;//①if(root->left == nullptr && root->right == nullptr)//递归出口{return presum;}int ret = 0;if(root->left != nullptr) ret += dfs(root->left,presum);//②③if(root->right!= nullptr) ret += dfs(root->right,presum);//④⑤return ret;//⑥}
};

例题3.二叉树剪枝

1.题目

题目链接：二叉树剪枝
给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

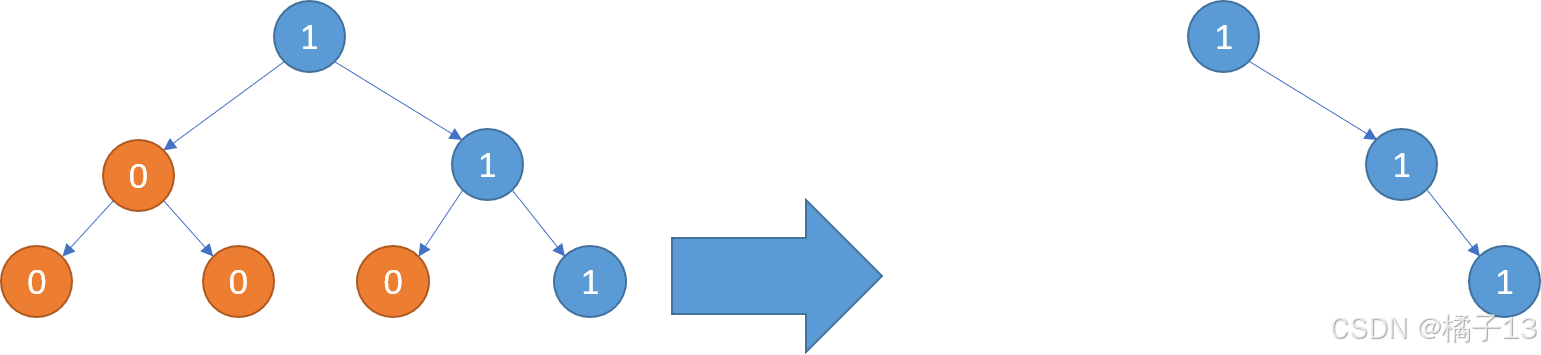
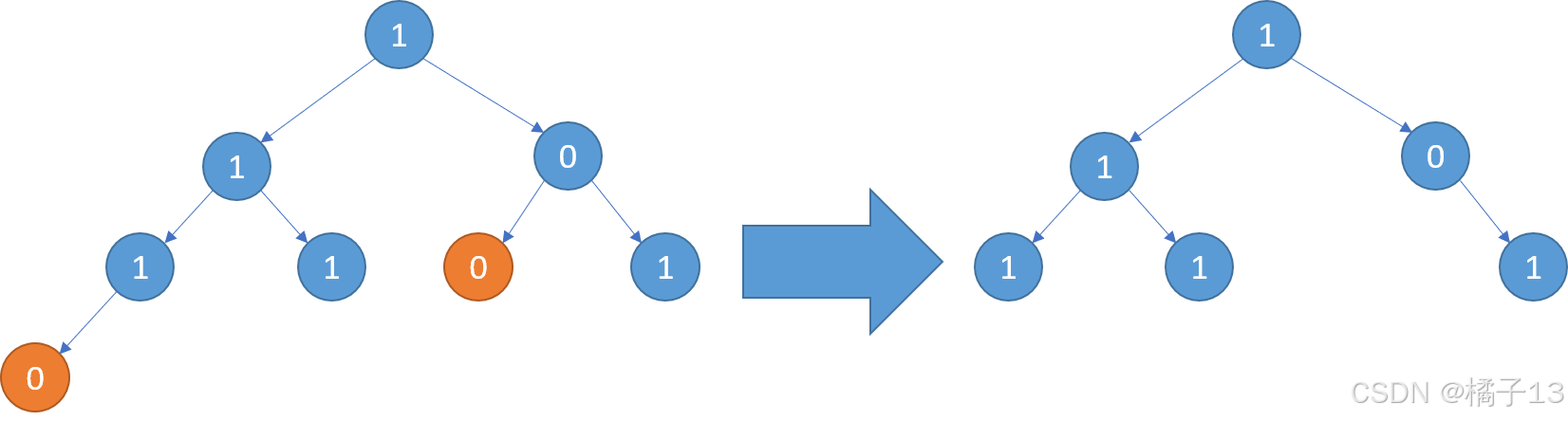
输入：root = [1,null,0,0,1] 输出：[1,null,0,null,1] 解释： 只有红色节点满足条件“所有不包含 1
的子树”。 右图为返回的答案。 示例 2：

输入：root = [1,0,1,0,0,0,1] 输出：[1,null,1,null,1] 示例 3：

输入：root = [1,1,0,1,1,0,1,0] 输出：[1,1,0,1,1,null,1]

提示：
树中节点的数目在范围 [1, 200] 内
Node.val 为 0 或 1

2.算法原理

通过决策树，抽象出递归的三个核心问题。
后序遍历
1.重复子问题——>函数头设计

TreeNode* dfs(TreeNode* root)

2.只关心一个子问题在做什么——>函数体的设计
1.处理左子树 root->left = pruneTree(root->left);
2.处理右子树 root->right = pruneTree(root->right);
3.判断

if(root->val == 0 && root->left == nullptr && root->right == nullptr)
{return nullptr;
}

3.递归的退出

root == nullptr 

3.编写代码

class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr){return nullptr;}root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->val == 0 && root->left == nullptr && root->right == nullptr){return nullptr;}return root;}
};

例题4.验证二叉搜索树

1.题目

题目链接：验证二叉搜索树
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

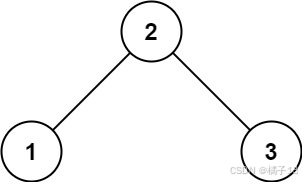
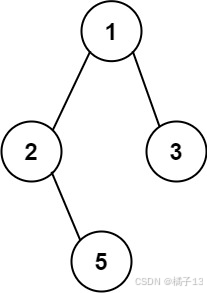
输入：root = [2,1,3] 输出：true
示例 2：

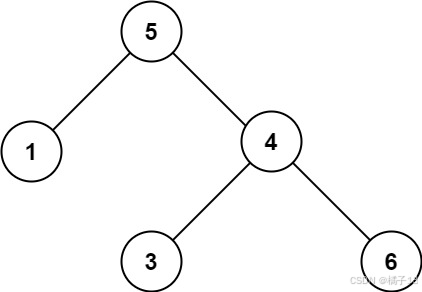
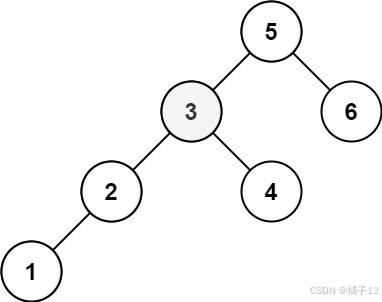
输入：root = [5,1,4,null,null,3,6] 输出：false 解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：
树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

2.算法原理

性质：二叉搜索树的中序遍历的结果是一个有序的序列。

策略1：左子树是二叉搜索树，当前节点也符合二叉搜索树定义，右子树也是二叉搜索树。

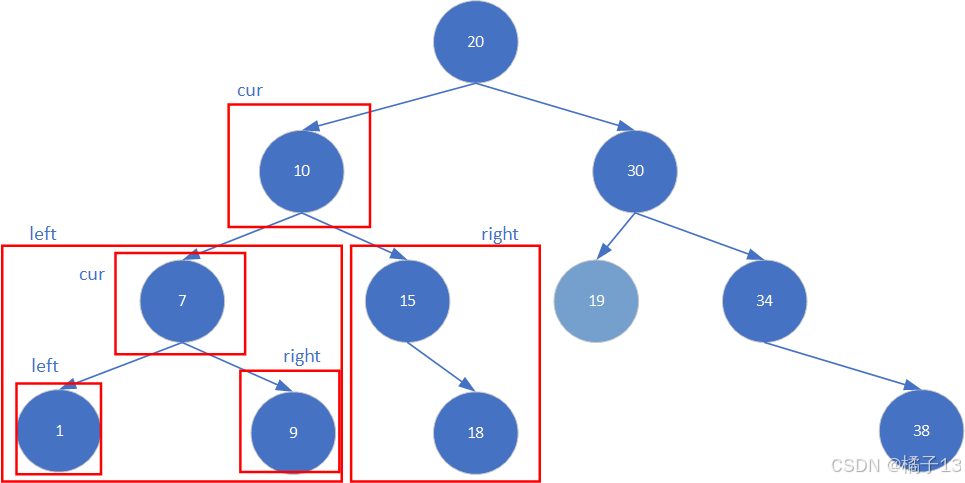
以这个图为例，只考虑左边的分支，left，right，cur是三个bool类型的数值，分别用来判定左子树是否是二叉搜索树，右子树是否是二叉搜索树，根节点是否满足二叉搜索树。若都满足，则返回三者的&，作为判断整个子树是否为二叉搜索树。

策略2：策略1的优化，加入剪枝，当找到不符合搜索二叉树的节点时，直接向上返回false即可，无需进行其他多余的遍历。

由于中序遍历顺序是，左→中→右，如果左子树不满足搜索二叉树，直接进行返回false，即左→判断→中→右，同理，若中间节点与左子树关系不满足搜索二叉树，直接进行返回false，即左→判断→中→判断→右。

1.设置全局变量的优势
设置全局变量prev，让其对比每个节点的数值，这样就不用在每次递归中传输变量记录节点的值了。

2.关于回溯

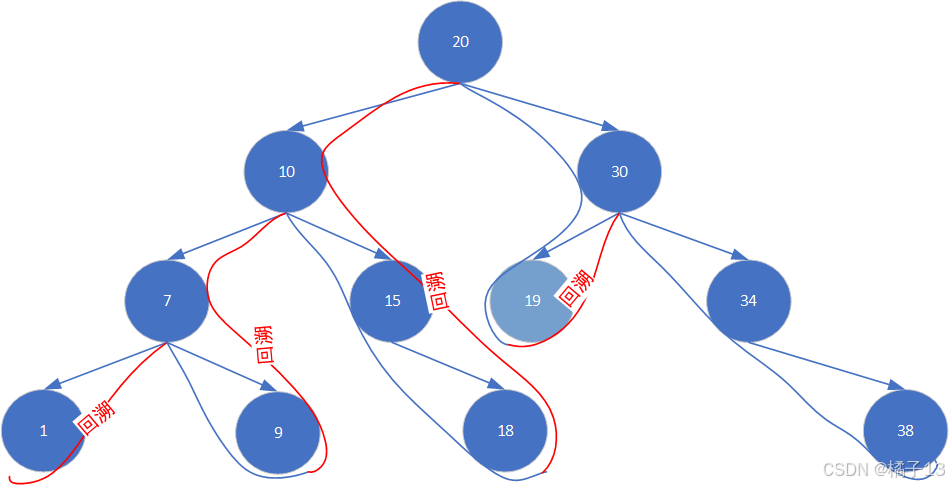
3.关于剪枝
作用：加快搜索过程。

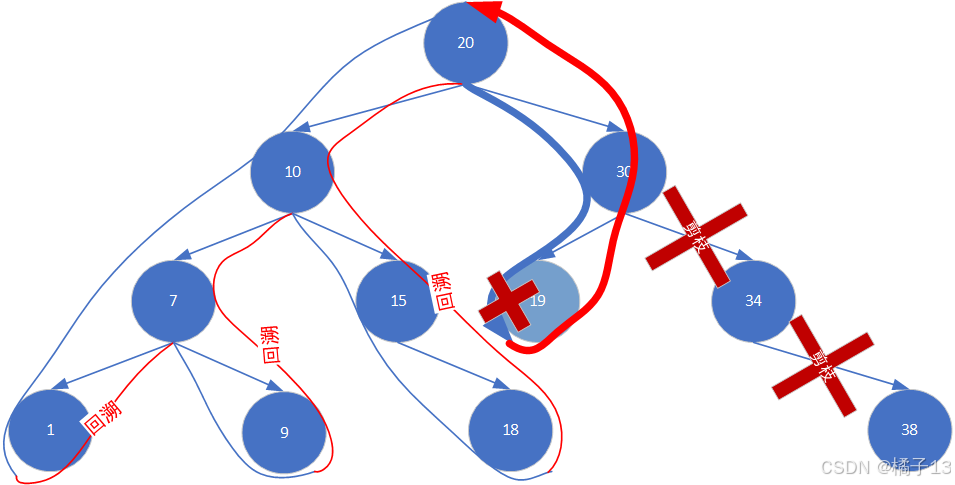
3.编写代码

策略1：左子树是二叉搜索树，当前节点也符合二叉搜索树定义，右子树也是二叉搜索树。

class Solution {
public:long prev = LONG_MIN;bool isValidBST(TreeNode* root) {if(root == nullptr){return true;}bool left = isValidBST(root->left);//左子树bool cur = false;//根节点if(root->val > prev){cur = true;}prev = root->val;bool right = isValidBST(root->right);//右节点return right && left && cur; }
};

策略2：策略1的优化，加入剪枝，当找到不符合搜索二叉树的节点时，直接向上返回false即可，无需进行其他多余的遍历。

class Solution {
public:long prev = LONG_MIN;bool isValidBST(TreeNode* root) {if(root == nullptr){return true;}bool left = isValidBST(root->left);//左子树if(left == false) return false;//剪枝bool cur = false;//根节点if(root->val > prev){cur = true;}//else//或者//{//return false;//剪枝//}if(left == false) return false;//剪枝prev = root->val;bool right = isValidBST(root->right);//右节点return right && left && cur; }
};

例题5.二叉树中第k小的元素

1.题目

题目链接：二叉树中第k小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

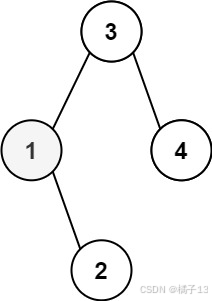
输入：root = [3,1,4,null,2], k = 1 输出：1
示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3 输出：3

提示：树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

2.算法原理

1.两个全局变量 count，ret + 中序遍历

• 通过中序遍历二叉搜索树（天然升序的性质）
• 每访问一个节点就将 count 减 1
• 当 count 减到 0 时，当前节点就是第 k 小的元素，将该元素保存在ret中
  
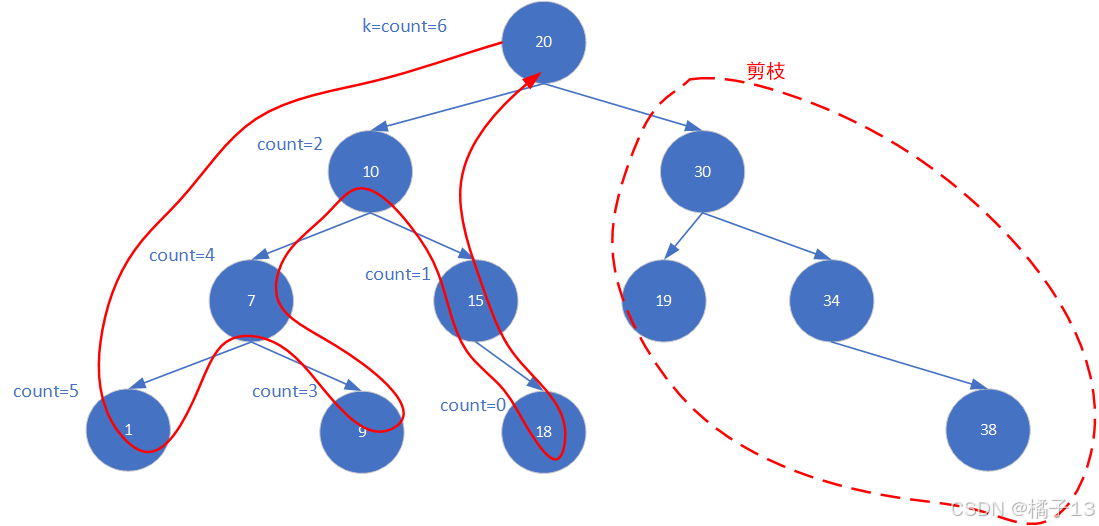
  2.剪枝优化
  左→判断→中→判断→右

1. 在访问当前节点之前（左子树遍历后），先检查count是否已经为 0，如果是则直接返回，不再处理当前节点和右子树。
2. 当找到目标元素（count减到 0 时），立即返回，不再遍历右子树。

3.编写代码

class Solution {
public:int count;int ret;int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode* root){if(root == nullptr)return;dfs(root->left);count--;if(count == 0)ret = root->val;dfs(root->right);}
};

加入剪枝优化

class Solution {
public:int count;int ret;int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode* root){if(root == nullptr)return;dfs(root->left);if(count == 0) return;//剪枝优化count--;if(count == 0){ret = root->val;return;//剪枝优化}dfs(root->right);}
};

例题6.二叉树的所有路径

1.题目

题目链接：二叉树的所有路径
给你一个二叉树的根节点 root ，按任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3,null,5] 输出：[“1->2->5”,“1->3”] 示例 2： 输入：root = [1]
输出：[“1”]

提示：
树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

2.算法原理

1.全局变量

vector<string> ret;

2.回溯→恢复现场
函数头

void dfs(root,path)//这里path变量传入的作用是“恢复现场”

函数体

• 是叶子节点
  将root->val追加在path上，注意此时是找到了一条完整的路径，ret.push_back()将完整路径保存。
• 不是叶子节点
  将root->val + “->”追加在path上.

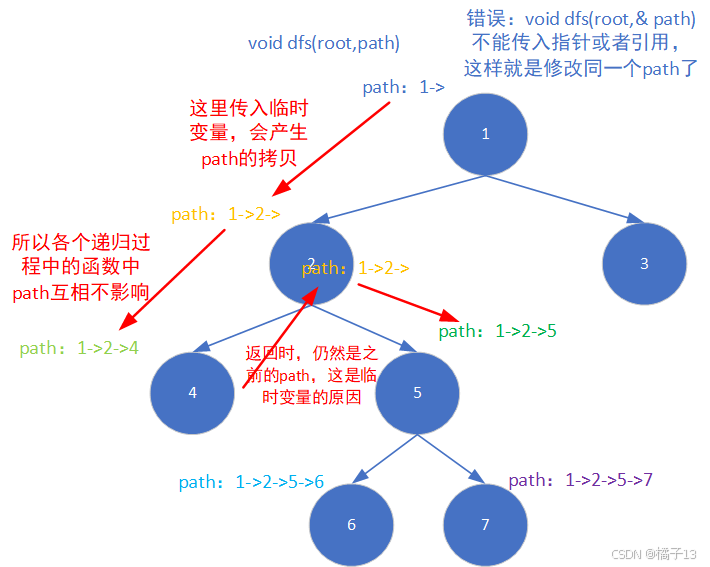
☆关于恢复现场

string path变量作全局变量——>只能手动恢复现场

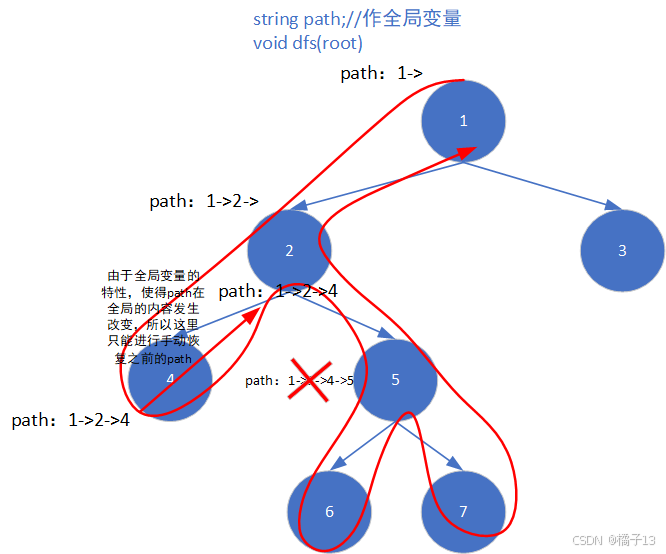
string path作函数参数，作为临时变量——>自动恢复现场

递归出口

root == nullptr  return

3.剪枝
无所谓，反正都要遍历！
一定要做的话，不进入空节点，检测到左或右子树为空的话，干脆不进入！

3.编写代码

class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {string path = "";dfs(root, path);return ret;}void dfs(TreeNode* root, string path)//不能带引用，否则无法实现自动“恢复现场”{if(root == nullptr)return;if(root->right == nullptr &&root->left == nullptr)//找到叶子节点，即找到一条完整路径{path += to_string(root->val);ret.push_back(path);}else{path += to_string(root->val);path += "->";}dfs(root->left,path);dfs(root->right,path);}};

class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {string path = "";dfs(root, path);return ret;}void dfs(TreeNode* root, string path)//不能带引用，否则无法实现自动“恢复现场”{if(root->right == nullptr &&root->left == nullptr)//找到叶子节点，即找到一条完整路径{path += to_string(root->val);ret.push_back(path);return;//剪枝，对于叶子节点，不用再看左右子树了，一定都是nullptr}else{path += to_string(root->val);path += "->";}if(root->left) dfs(root->left,path);//剪枝，左子树为空的话，直接不进入if(root->right) dfs(root->right,path);}};