百度之星2025（第二场）

GCD Maximum

题目
签到，打表找规律。

//打表代码
#include<bits/stdc++.h>
using namespace std;
int main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);for (int n = 1; n <=6; n ++) {vector<int> v(n);for(int i = 0;i < n; i++) {v[i] = i + 1;}vector<int>vc;int maxh = 0;do {int gg = 0;for(int i = 0;i < n; i++) {gg = __gcd((i + 1) * v[i],gg);}if (gg > maxh) {vc = v;maxh = gg;}}while (next_permutation(v.begin(), v.end()));for(int i = 0;i < n; i++) {cout<<vc[i]<<" ";}cout<<endl;}return 0;
}

观察到，
奇数是为1 ~ n 的序列，偶数时两两取反

#include<bits/stdc++.h> using namespace std;int main( )
{int n;cin>>n;if(n % 2){for(int i = 1; i<=n ;i++){cout<<i<<' ';}}else{vector<int>v;for(int i = 1; i <= n; i++){v.push_back(i);}for(int i = 0;i<v.size();i+=2){swap(v[i],v[i+1]);}for(int i =0 ;i < v.size();i++){cout<<v[i]<<' ';}}return 0;
}

Equal

题目
排序 + 枚举。
不难想出，用情况一时一定是要把所有数字全部化为0。
所以我们要比较两种情况，分别是1.全化为零 2.全化为最多的数字。

#include<bits/stdc++.h> 
#define int long long
const int N = 2e5+5;
using namespace std;
int a[N];
void solve(){int n,x,y;unordered_map<int,int>mp;cin>>n>>x>>y;for(int i = 1; i <= n; i++){cin>>a[i];mp[a[i]]++;}sort(a + 1, a + n + 1);int maxh = 0 , ans = 0;for(auto&[x,y]:mp){maxh = max(maxh,y);}ans = (n - maxh) * y;for(int i = 1; i <= n; i++){ans = min(ans,a[i] * x + (n - i) * y);}cout << ans << '\n';
}
signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int T;cin>>T;while(T--){solve();}return 0;
}

Pair Counting

题目
图论 + 分类
sum【i】：表示连接着i节点的叶子节点的个数。
正着算优美的对数太多，我们用 优美 = 总体 - 不优美的个数
不优美的情况：
如果情况不明白可以看官方讲解。
1. 两个节点直接相连
2.

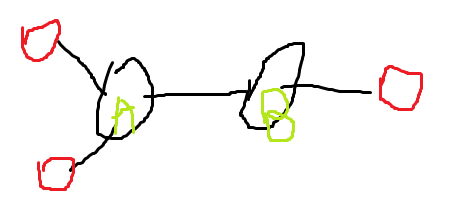
左红色和右红色组成的节点对都不是优美的。即相连边的叶子节点数量乘积（乘法原理)。

我看好多人都忘了n = 2这种情况（虽然也能过去，这是个黑客样例）
1
2
1 2
要考虑到两个节点连成一条线时，notbutiy已经在（n - 1)这种情况中算过了。如果不特殊考虑，那么在sum[i]中的情况依然是两个节点的路径不优美，即被算了两次。

#include<bits/stdc++.h> 
#define int long long
using namespace std;
void solve(){int n;cin>>n;if(n == 2){cout<<0<<'\n';return;}vector<vector<int>>e(n + 1);vector<int>dig(n + 1,0);vector<int>sum(n + 1,0);for(int i = 1; i < n; i ++){int a,b;cin>>a>>b;dig[a] ++, dig[b] ++;e[a].push_back(b);e[b].push_back(a);}int notbutiy = 0;for(int i = 1; i <= n; i++){for(int j = 0; j < e[i].size(); j ++){int t = e[i][j];if(dig[t] == 1){sum[i]++;}}}for(int i = 1; i <= n; i++){for(int j = 0; j < e[i].size(); j ++){int t = e[i][j];notbutiy += sum[i] * sum[t];}}int ans = n * (n - 1) / 2 - (n - 1) - notbutiy / 2;cout << ans <<'\n';
}
signed main()
{ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int T;cin>>T;while(T--){solve();}return 0;
}

Yummy

题目
状压dp
首先这个$k^i$就可以看作将s_i* v_i在进制中向左移动i位。这样就可以发现一个结论。
核心结论：第 i 项 $s_i\cdot v_i\cdot k^i$ 的绝对值，大于前 (i-1) 项总和的绝对值。 这就意味着，第 i 项的符号，直接决定了前 i 项总和的符号（除非 v_i = 0）。

其中 f [ 0 ， 1 ， 2]分别表示总和为 0 ， 正数 ，负数 ，的情况数。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
void solve() {int n, k;cin >> n >> k;vector<int> s(n);for (int i = 0; i < n; i++) {cin >> s[i];}int f[3] = {1, 0, 0}; for (int i = 0; i < n; i++) {int g[3] = {0, 0, 0};if (s[i] == 1) {g[0] = (g[0] + f[0]) % mod;g[2] = (g[2] + f[0]) % mod;g[0] = (g[0] + f[1]) % mod;g[2] = (g[2] + f[2]) % mod;} else {g[0] = (g[0] + f[0]) % mod;g[1] = (g[1] + f[0]) % mod;g[1] = (g[1] + f[1]) % mod;g[0] = (g[0] + f[2]) % mod;}f[0] = g[0];f[1] = g[1];f[2] = g[2];}cout << f[0] % mod << "\n";
}
signed main() {ios_base::sync_with_stdio(false);cin.tie(0);int T;cin >> T;while (T--) {solve();}return 0;
}

其他题目之后补