@[TOC](位运算) # 常见位运算总结

常见位运算总结

位1的个数

191. 位1的个数

给定一个正整数 n，编写一个函数，获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数（也被称为汉明重量）。
示例 1：
输入：n = 11
输出：3
解释：输入的二进制串 1011 中，共有 3 个设置位。
示例 2：
输入：n = 128
输出：1
解释：输入的二进制串 10000000 中，共有 1 个设置位。
示例 3：
输入：n = 2147483645
输出：30
解释：输入的二进制串 1111111111111111111111111111101 中，共有 30 个设置位。
提示：
1 <= n <= 231 - 1
进阶：
如果多次调用这个函数，你将如何优化你的算法？

方法一：逐位判断
根据 与运算 定义，设二进制数字 n ，则有：
若 n&1=0 ，则 n 二进制 最右一位 为 0 。
若 n&1=1 ，则 n 二进制 最右一位 为 1 。
根据以上特点，考虑以下 循环判断 ：
判断 n 最右一位是否为 1 ，根据结果计数。
将 n 右移一位（本题要求把数字 n 看作无符号数，因此使用 无符号右移 操作）。

public class Solution {public int hammingWeight(int n) {int res = 0;while (n != 0) {res += n & 1;n >>>= 1;}return res;}
}

复杂度分析：
时间复杂度 O(logn) ： 此算法循环内部仅有 移位、与、加 等基本运算，占用 O(1) ；逐位判断需循环 log₂ n 次，其中 log₂n 代表数字 n 最高位 1 的所在位数。
空间复杂度 O(1) ： 变量 res 使用常数大小额外空间。
方法二：巧用 n&(n−1)
(n−1) 作用： 二进制数字 n 最右边的 1 变成 0 ，此 1 右边的 0 都变成 1 。
n&(n−1) 作用： 二进制数字 n 最右边的 1 变成 0 ，其余不变。

public class Solution {public int hammingWeight(int n) {int res = 0;while (n != 0) {res++;n &= n - 1;}return res;}
}

复杂度分析：
时间复杂度 O(M) ： n&(n−1) 操作仅有减法和与运算，占用 O(1) ；设 M 为二进制数字 n 中 1 的个数，则需循环 M 次（每轮消去一个1），占用 O(M) 。
空间复杂度 O(1) ： 变量 res 使用常数大小额外空间。

比特位计数

338. 比特位计数

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1：
输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10
示例 2：
输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示：
0 <= n <= 105
进阶：
很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

方法一：枚举二进制为1的位
对于任意整数 x，令 x=x & (x−1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的「一比特数」。
对于给定的 n，计算从 0 到 n 的每个整数的「一比特数」的时间都不会超过 O(logn)，因此总时间复杂度为 O(nlogn)。

class Solution {public int[] countBits(int n) {int[] bits=new int[n+1];for(int i=0;i<=n;i++){int ones=0;int x=i;while(x>0){x&=(x-1);ones++;}bits[i]=ones;}return bits;}
}

复杂度分析
时间复杂度：O(nlogn)。需要对从 0 到 n 的每个整数使用计算「一比特数」，对于每个整数计算「一比特数」的时间都不会超过 O(logn)。
空间复杂度：O(1)。除了返回的数组以外，空间复杂度为常数。
方法二：动态规划——最低设置位
定义正整数 x 的「最低设置位」为 x 的二进制表示中的最低的 1 所在位。例如，10 的二进制表示是 1010 (2) ，其最低设置位为 2，对应的二进制表示是 10 (2) 。
令 y=x & (x−1)，则 y 为将 x 的最低设置位从 1 变成 0 之后的数，显然 0≤y<x，bits[x]=bits[y]+1。因此对任意正整数 x，都有 bits[x]=bits[x & (x−1)]+1。
遍历从 1 到 n 的每个正整数 i，计算 bits 的值。最终得到的数组 bits 即为答案。

class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 1; i <= n; i++) {bits[i] = bits[i & (i - 1)] + 1;}return bits;}
}

复杂度分析
时间复杂度：O(n)。对于每个整数，只需要 O(1) 的时间计算「一比特数」。
空间复杂度：O(1)。除了返回的数组以外，空间复杂度为常数。

汉明距离

461. 汉明距离

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y，计算并返回它们之间的汉明距离。
示例 1：
输入：x = 1, y = 4
输出：2
解释：
1 (0 0 0 1)
4 (0 1 0 0)
示例 2：
输入：x = 3, y = 1
输出：1
提示：
0 <= x, y <= 231 - 1

前言
汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。
根据以上定义，我们使用异或运算，记为 ⊕，当且仅当输入位不同时输出为 1。
计算 x 和 y 之间的汉明距离，可以先计算 x⊕y，然后统计结果中等于 1 的位数。
现在，原始问题转换为位计数问题。位计数有多种思路
方法一：内置位计数功能
思路及算法
大多数编程语言都内置了计算二进制表达中 1 的数量的函数。在工程中，我们应该直接使用内置函数。

class Solution {public int hammingDistance(int x, int y) {return Integer.bitCount(x ^ y);}
}

复杂度分析
时间复杂度：O(1)。不同语言的实现方法不一，我们可以近似认为其时间复杂度为 O(1)。
空间复杂度：O(1)。
方法二：Brian Kernighan 算法
思路及算法
该算法可以被描述为这样一个结论：记 f(x) 表示 x 和 x−1 进行与运算所得的结果（即 f(x)=x & (x−1)），那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。
基于该算法，当我们计算出 s=x⊕y，只需要不断让 s=f(s)，直到 s=0 即可。这样每循环一次，s 都会删去其二进制表示中最右侧的 1，最终循环的次数即为 s 的二进制表示中 1 的数量。

class Solution {public int hammingDistance(int x, int y) {int s = x ^ y, ret = 0;while (s != 0) {s &= s - 1;ret++;}return ret;}
}

复杂度分析
时间复杂度：O(logC)，其中 C 是元素的数据范围，在本题中 logC=log2³¹ =31
空间复杂度：O(1)
lowbit
熟悉树状数组的同学都知道，lowbit 可以快速求得 x 二进制表示中最低位 1 表示的值。
因此我们可以先将 x 和 y 进行异或，再统计异或结果中 1 的个数。

class Solution {int lowbit(int x) {return x & -x;}public int hammingDistance(int x, int y) {int ans = 0;for (int i = x ^ y; i > 0; i -= lowbit(i)) ans++;return ans;}
}

时间复杂度：O( C )，C 最多为 32
空间复杂度：O(1)

只出现一次的数字

136. 只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。
示例 1 ：
输入：nums = [2,2,1]
输出：1
示例 2 ：
输入：nums = [4,1,2,1,2]
输出：4
示例 3 ：
输入：nums = [1]
输出：1
提示：
1 <= nums.length <= 3 * 10⁴
-3 * 10⁴ <= nums[i] <= 3 * 10⁴
除了某个元素只出现一次以外，其余每个元素均出现两次。

方法一：位运算
如果不考虑时间复杂度和空间复杂度的限制，这道题有很多种解法，可能的解法有如下几种。

• 使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。
• 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。
• 使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

上述三种解法都需要额外使用 O(n) 的空间，其中 n 是数组长度。
如何才能做到线性时间复杂度和常数空间复杂度呢？
答案是使用位运算。对于这道题，可使用异或运算 ⊕。异或运算有以下三个性质。

• 任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
• 任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
• 异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

class Solution {public int singleNumber(int[] nums) {int single = 0;for (int num : nums) {single ^= num;}return single;}
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组长度。只需要对数组遍历一次。
空间复杂度：O(1)。

只出现一次的数字 III

260. 只出现一次的数字 III

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1：
输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。
示例 2：
输入：nums = [-1,0]
输出：[-1,0]
示例 3：
输入：nums = [0,1]
输出：[1,0]
提示：
2 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
除两个只出现一次的整数外，nums 中的其他数字都出现两次

方法一：哈希表
朴素的做法是利用哈希表进行统计，最后将统计次数为 1 的元素加入答案。

class Solution {public int[] singleNumber(int[] nums) {Map<Integer, Integer> map = new HashMap<>();for (int i : nums) map.put(i, map.getOrDefault(i, 0) + 1);int[] ans = new int[2];int idx = 0;for (int i : nums) {if (map.get(i) == 1) ans[idx++] = i;}return ans;}
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组 nums 的长度。
空间复杂度：O(n)，即为哈希映射需要使用的空间。
法二：位运算：异或
利用除答案以外的元素均出现两次，我们可以先对 nums 中的所有元素执行异或操作，得到 sum，sum 为两答案的异或值（sum 必然不为0）。
然后取 sum 二进制表示中为 1 的任意一位 k，sum 中的第 k 位为 1 意味着两答案的第 k 位二进制表示不同。
对 nums 进行遍历，对第 k 位分别为 0 和 1 的元素分别求异或和（两答案必然会被分到不同的组），即为答案。

解释一下最后一个循环的作用：因为已知sum的第k位为1，说明这两个数的第k位一个为0，一个为1，因此可以将nums中的元素分成两组，一组里边的元素的第k位都为0，另一组都为1，对每一组的元素分别求异或，因为其他的元素都有两个，异或的结果都为0，所以每一组的异或结果即为答案之一。

class Solution {public int[] singleNumber(int[] nums) {int sum = 0;for (int i : nums) sum ^= i;int k = -1;for (int i = 31; i >= 0 && k == -1; i--) {if (((sum >> i) & 1) == 1) k = i;}int[] ans = new int[2];for (int i : nums) {if (((i >> k) & 1) == 1) ans[1] ^= i;else ans[0] ^= i;}return ans;}
}

或
我们可以使用位运算 x & -x 取出 x 的二进制表示中最低位那个 1，设其为第 l 位，那么 x1 和 x2 中的某一个数的二进制表示的第 l 位为 0，另一个数的二进制表示的第 l 位为 1。在这种情况下，x1⊕x2 的二进制表示的第 l 位才能为 1。
这样一来，我们就可以把 nums 中的所有元素分成两类，其中一类包含所有二进制表示的第 l 位为 0 的数，另一类包含所有二进制表示的第 l 位为 1 的数。
我们将每一类的元素全部异或起来，那么其中一类会得到 x1 ，另一类会得到 x2 。这样我们就找出了这两个只出现一次的元素。
（推荐代码）

class Solution {public int[] singleNumber(int[] nums) {int [] res=new int [2];int n=nums.length,ans=0,flag=1;for(int i=0;i<n;++i){ans^=nums[i];}//取最低位的1；flag=ans&(-ans);for(int i=0;i<n;++i){//分组，最低位的1一定是由两个只出现一次的数字造成的；if((nums[i]&flag)==0){res[0]^=nums[i];}else{res[1]^=nums[i];}}return res;}
}

时间复杂度：O(n)，其中 n 是数组 nums 的长度。
空间复杂度：O(1)

1. 判断字符是否唯⼀（easy）

题⽬链接：⾯试题 01.01. 判定字符是否唯⼀
题⽬描述：

实现⼀个算法，确定⼀个字符串 s 的所有字符是否全都不同。
⽰例 1：
输⼊: s = “leetcode”
输出: false
⽰例 2：
输⼊: s = “abc”
输出: true
限制：
0 <= len(s) <= 100
s[i]仅包含⼩写字⺟
如果你不使⽤额外的数据结构，会很加分。

解法（位图的思想）：

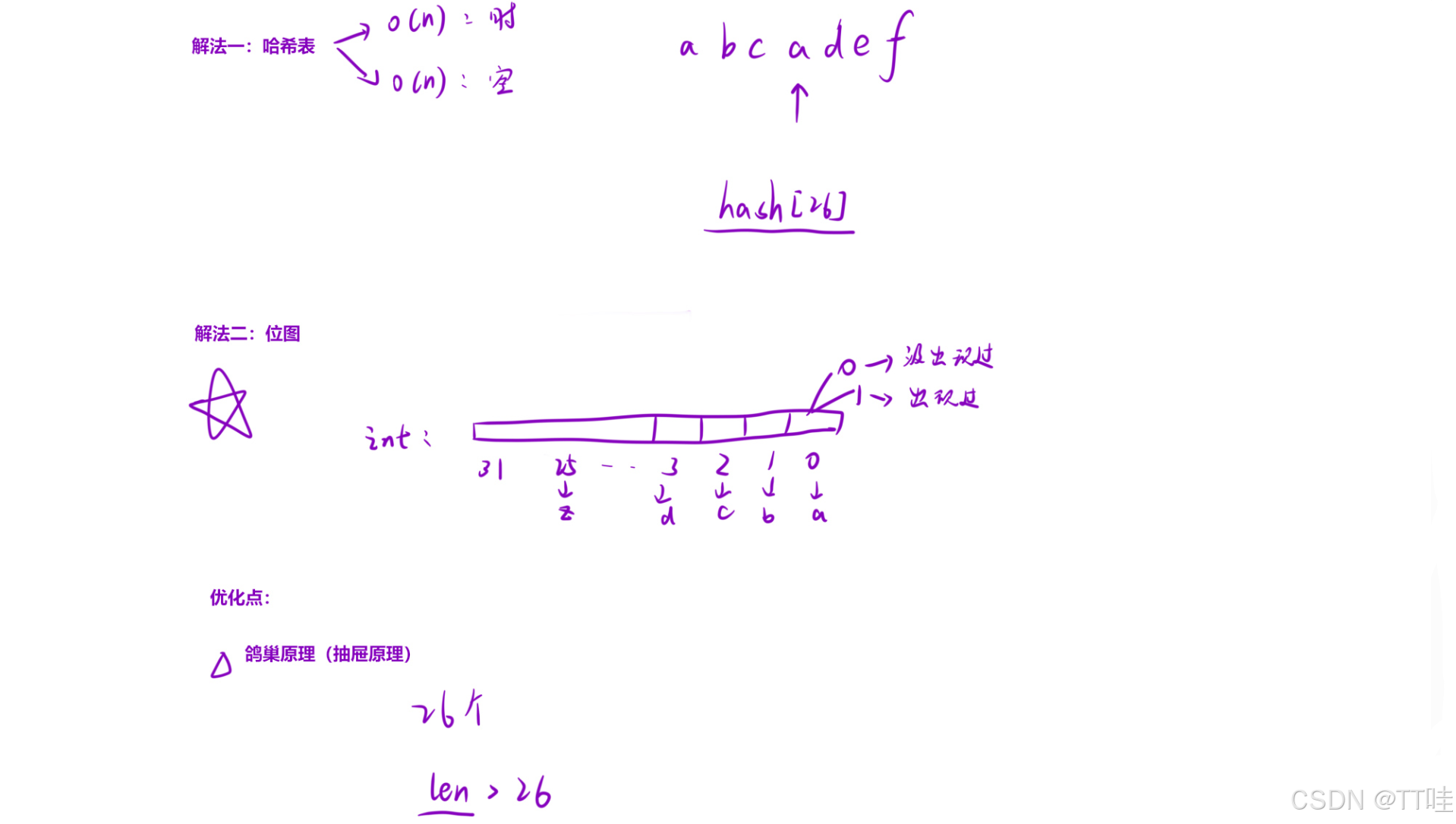
算法思路：
利⽤「位图」的思想，每⼀个「⽐特位」代表⼀个「字符」，⼀个 int 类型的变量的 32 位⾜够表⽰所有的⼩写字⺟。⽐特位⾥⾯如果是 0 ，表⽰这个字符没有出现过。⽐特位⾥⾯的值是 1 ，表⽰该字符出现过。
那么我们就可以⽤⼀个「整数」来充当「哈希表」。
C++ 算法代码：

class Solution{
public:bool isUnique(string astr){// 利⽤鸽巢原理来做的优化if(astr.size() > 26) return false; int bitMap = 0;for(auto ch : astr){int i = ch - 'a';// 先判断字符是否已经出现过if(((bitMap >> i) & 1) == 1) return false;// 把当前字符加⼊到位图中bitMap |= 1 << i;}return true;}
}

Java 算法代码：

class Solution {public boolean isUnique(String astr) {// 利⽤鸽巢原理来做优化if(astr.length() > 26) return false;int bitMap = 0;for(int i = 0; i < astr.length(); i++){int x = astr.charAt(i) - 'a';// 先判断字符是否在位图中if(((bitMap >> x) & 1) == 1) return false;// 把当前字符加⼊到位图中bitMap |= 1 << x;}return true;}
}

(注意运算符优先级)

2. 丢失的数字（easy）

题⽬链接：268. 丢失的数字
题⽬描述：

给定⼀个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。
⽰例 1：
输⼊：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没
有出现在 nums 中。
⽰例 2：
输⼊：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没
有出现在 nums 中。
⽰例 3：
输⼊：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没
有出现在 nums 中。
⽰例 4：
输⼊：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。
提⽰：
n == nums.length
1 <= n <= 10^4
0 <= nums[i] <= n
nums 中的所有数字都 独⼀⽆⼆
进阶：你能否实现线性时间复杂度、仅使⽤额外常数空间的算法解决此问题?

法1：哈希集合

使用哈希集合，可以将时间复杂度降低到 O(n)。

首先遍历数组 nums，将数组中的每个元素加入哈希集合，然后依次检查从 0 到 n 的每个整数是否在哈希集合中，不在哈希集合中的数字即为丢失的数字。由于哈希集合的每次添加元素和查找元素的时间复杂度都是 O(1)，因此总时间复杂度是 O(n)。

class Solution {public int missingNumber(int[] nums) {Set<Integer> set = new HashSet<Integer>();int n = nums.length;for (int i = 0; i < n; i++) {set.add(nums[i]);}int missing = -1;for (int i = 0; i <= n; i++) {if (!set.contains(i)) {missing = i;break;}}return missing;}
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组 nums 的长度。遍历数组 nums 将元素加入哈希集合的时间复杂度是 O(n)，遍历从 0 到 n 的每个整数并判断是否在哈希集合中的时间复杂度也是 O(n)。
空间复杂度：O(n)，其中 n 是数组 nums 的长度。哈希集合中需要存储 n 个整数。

法2（位运算）：

算法思路：
设数组的⼤⼩为 n ，那么缺失之前的数就是 [0, n] ，数组中是在 [0, n] 中缺失⼀个数形成的序列。
如果我们把数组中的所有数，以及 [0, n] 中的所有数全部「异或」在⼀起，那么根据「异或」运算的「消消乐」规律，最终的异或结果应该就是缺失的数~
C++ 算法代码：

class Solution
{
public:int missingNumber(vector<int>& nums) {int ret = 0;for(auto x : nums) ret ^= x;for(int i = 0; i <= nums.size(); i++) ret ^= i;return ret;}
}

Java 算法代码：

class Solution {public int missingNumber(int[] nums) {int ret = 0;for(int x : nums) ret ^= x;for(int i = 0; i <= nums.length; i++) ret ^= i;return ret;}
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要对 2n+1 个数字计算按位异或的结果。
空间复杂度：O(1)。

3.两整数之和（medium）

题⽬链接：371. 两整数之和
题⽬描述：

给你两个整数 a 和 b ，不使⽤ 运算符 + 和 - ，计算并返回两整数之和。
⽰例 1：
输⼊：a = 1, b = 2
输出：3
⽰例 2：
输⼊：a = 2, b = 3
输出：5
提⽰：
-1000 <= a, b <= 1000

解法（位运算）：

算法思路：
◦ 异或 ^ 运算本质是「⽆进位加法」；
◦ 按位与 & 操作能够得到「进位」；
◦ 然后⼀直循环进⾏，直到「进位」变成 0 为⽌
可以发现，对于整数 a 和 b：
在不考虑进位的情况下，其无进位加法结果为 a⊕b。
而所有需要进位的位为 a & b，进位后的进位结果为 (a & b) << 1。
于是，我们可以将整数 a 和 b 的和，拆分为 a 和 b 的无进位加法结果与进位结果的和。因为每一次拆分都可以让需要进位的最低位至少左移一位，又因为 a 和 b 可以取到负数，所以我们最多需要 log(max_int) 次拆分即可完成运算。
因为有符号整数用补码来表示，所以以上算法也可以推广到 0 和负数。
代码

class Solution {public int getSum(int a, int b) {while (b != 0) {int carry = (a & b) << 1;// 计算进位a = a ^ b;// 先算出⽆进位相加的结果b = carry;}return a;}
}

复杂度分析
时间复杂度：O(log(max_int))，其中我们将执行位运算视作原子操作。
空间复杂度：O(1)。

4.只出现⼀次的数字 II（medium）

题⽬链接：137. 只出现⼀次的数字 II
题⽬描述：

给你⼀个整数数组 nums ，除某个元素仅出现 ⼀次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了⼀次的元素。
你必须设计并实现线性时间复杂度的算法且不使⽤额外空间来解决此问题。
⽰例 1：
输⼊：nums = [2,2,3,2]
输出：3
⽰例 2：
输⼊：nums = [0,1,0,1,0,1,99]
输出：99
提⽰：
1 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
nums 中，除某个元素仅出现 ⼀次 外，其余每个元素都恰出现 三次

法1：哈希表

思路与算法
我们可以使用哈希映射统计数组中每个元素的出现次数。对于哈希映射中的每个键值对，键表示一个元素，值表示其出现的次数。
在统计完成后，我们遍历哈希映射即可找出只出现一次的元素。
代码

class Solution {public int singleNumber(int[] nums) {Map<Integer, Integer> freq = new HashMap<Integer, Integer>();for (int num : nums) {freq.put(num, freq.getOrDefault(num, 0) + 1);}int ans = 0;for (Map.Entry<Integer, Integer> entry : freq.entrySet()) {int num = entry.getKey(), occ = entry.getValue();if (occ == 1) {ans = num;break;}}return ans;}
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组的长度。
空间复杂度：O(n)。哈希映射中包含最多 ⌊n/3⌋+1 个元素，即需要的空间为 O(n)。

法2：⽐特位计数

算法思路：
设要找的数位 ret 。
由于整个数组中，需要找的元素只出现了「⼀次」，其余的数都出现的「三次」，因此我们可以根据所有数的「某⼀个⽐特位」的总和 %3 的结果，快速定位到 ret 的「⼀个⽐特位上」的值是0 还是 1 。
这样，我们通过 ret 的每⼀个⽐特位上的值，就可以将 ret 给还原出来。
C++ 算法代码：

class Solution
{
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < 32; i++) // 依次去修改 ret 中的每⼀位{int sum = 0;for(int x : nums) // 计算nums中所有的数的第 i 位的和if(((x >> i) & 1) == 1)sum++;sum %= 3;if(sum == 1) ret |= 1 << i;}return ret;}
}

Java 算法代码：

class Solution{public int singleNumber(int[] nums) {int ret = 0;for(int i = 0; i < 32; i++) { // 依次修改 ret 中的每⼀个⽐特位int sum = 0;for(int x : nums) // 统计 nums 中所有的数的第 i 位的和if(((x >> i) & 1) == 1)sum++;sum %= 3;if(sum == 1) ret |= 1 << i;}return ret;}
}

5.消失的两个数字（hard）

题⽬链接：⾯试题 17.19. 消失的两个数字
题⽬描述：

给定⼀个数组，包含从 1 到 N 所有的整数，但其中缺了两个数字。你能在 O(N) 时间内只⽤ O(1) 的
空间找到它们吗？
以任意顺序返回这两个数字均可。
⽰例 1:
输⼊: [1]
输出: [2,3]
⽰例 2:
输⼊: [2,3]
输出: [1,4]
提⽰：
nums.length <= 30000

解法（位运算）：

算法思路：
本题就是 268. 丢失的数字 + 260. 只出现⼀次的数字 III 组合起来的题。
先将数组中的数和 [1, n + 2] 区间内的所有数「异或」在⼀起，问题就变成了：有两个数出现了「⼀次」，其余所有的数出现了「两次」。进⽽变成了 260. 只出现⼀次的数字 III 这道题。

Java 算法代码：

class Solution{public int[] missingTwo(int[] nums) {// 1. 先把所有的数异或在⼀起int tmp = 0;for(int x : nums) tmp ^= x;for(int i = 1; i <= nums.length + 2; i++) tmp ^= i;// 2. 找出 a，b 两个数⽐特位不同的那⼀位int diff = 0;while(true){if(((tmp >> diff) & 1) == 1) break;else diff++;}// 3. 将所有的数按照 diff 位不同，分两类异或int[] ret = new int[2];for(int x : nums)if(((x >> diff) & 1) == 1) ret[1] ^= x;else ret[0] ^= x;for(int i = 1; i <= nums.length + 2; i++)if(((i >> diff) & 1) == 1) ret[1] ^= i;else ret[0] ^= i;return ret;}
}

求解方法是利用「异或」+「lowbit」。

由于我们明确了是在 [1,n+2] 中缺失了两个数，我们可以先通过异或 [1,n+2] 以及所有的 nums[i] 来得到缺失两个数值异或和 t。

我们知道异或结果二进制表示为 1 代表了两缺失值该位置数值不同（一个该位置 0，另一个该位置为 1），我们可以根据异或和 t 中任意一位为 1 的位置来将两个缺失值划分到两组中。

更加优雅的方式是使用 lowbit 操作：d = t & -t 可快速得到只保留 t 中最低位 1 的对应数值。

随后将 [1,n+2] 中满足 i & d != 0 的所有 i（含义为对应位置为 1 的数值）与 nums[i] 中满足 nums[i] & d != 0 的所有 nums[i]（含义为对应位置为 1 的数值） 进行异或，最终能够确定其中一个缺失值，再结合最开始的异或和 t 即可确定另外一个缺失值。

更简便代码

class Solution {public int[] missingTwo(int[] nums) {// 1. 先把所有的数异或在⼀起int n = nums.length + 2, cur = 0;for (int i = 1; i <= n; i++) cur ^= i;for (int x : nums) cur ^= x;// 2. 找出 a，b 两个数⽐特位不同的那⼀位int t = cur, d = cur & -cur;// 3. 将所有的数按照 diff 位不同，分两类异或cur = 0;for (int i = 1; i <= n; i++) {if ((d & i) != 0) cur ^= i;}for (int x : nums) {if ((d & x) != 0) cur ^= x;}return new int[]{cur, t ^ cur};}
}

时间复杂度：O(n)
空间复杂度：O(1)
注意：
是if ((d & i) != 0) cur ^= i;不是if (d & i != 0) cur ^= i;（必须加括号）