数据结构(C语言篇):(十六)插入排序
目录
前言
一、排序的概念以及运用
1.1 概念
1.2 运用
1.3 常见的排序算法
二、插入排序
2.1 直接插入排序
2.2 希尔排序
2.2.1 希尔排序特性总结
2.2.2 希尔排序的时间复杂度计算
总结
前言
插入排序作为一种经典的排序算法,以其简洁的实现和直观的逻辑在计算机科学教育中占据重要地位。它通过逐步构建有序序列,将未排序元素逐个插入到已排序部分的正确位置,体现了分治思想在算法设计中的基础应用。尽管其时间复杂度在平均和最坏情况下达到O(n²),但插入排序在小规模数据或近乎有序的数据集上表现优异,甚至优于某些高级排序算法。该算法不仅为理解更复杂的排序技术奠定基础,其原地排序特性(空间复杂度O(1))和稳定性也使其在实际场景中仍具实用价值。本文将系统解析插入排序的核心原理、实现细节及性能优化策略,帮助读者掌握这一基础算法的本质与变体应用。
一、排序的概念以及运用
1.1 概念
排序是将一组数据按照特定规则重新排列的过程,通常以升序或降序为基准。排序后的数据更易于检索、统计或分析,是计算机科学和数据处理中的基础操作。
1.2 运用
排序在我们的日常生活中有着很多运用,比如购物筛选排序和院校排名系统等。购物筛选排序是电商平台中帮助用户快速找到符合需求的商品功能,通常基于价格、销量、评价、上新时间等维度进行分类和优先级排列。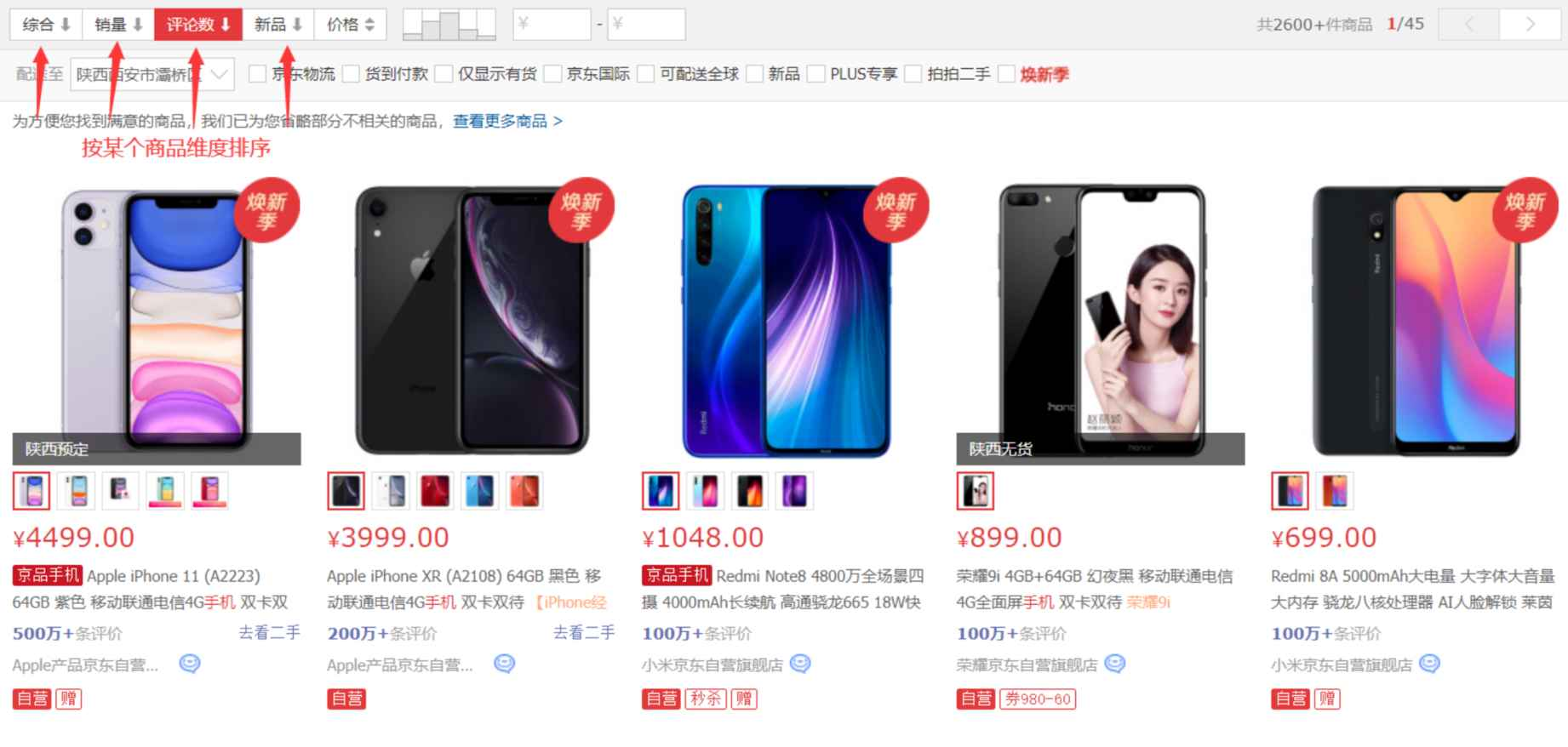
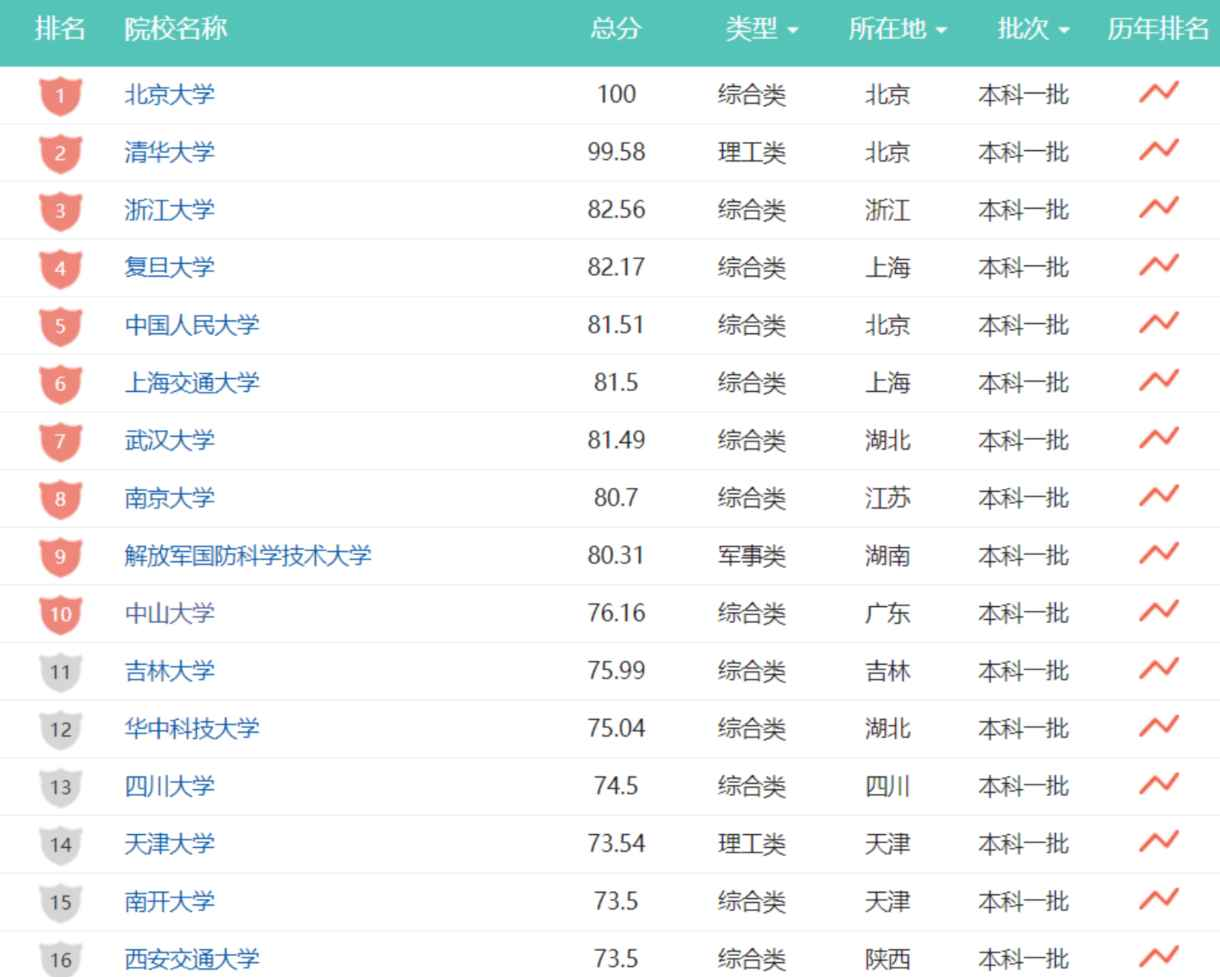
而院校排名通常则根据学术声誉调查、研究成果指标、师生比例、国际化程度、就业竞争力等因素综合对院校实力进行排序。
1.3 常见的排序算法
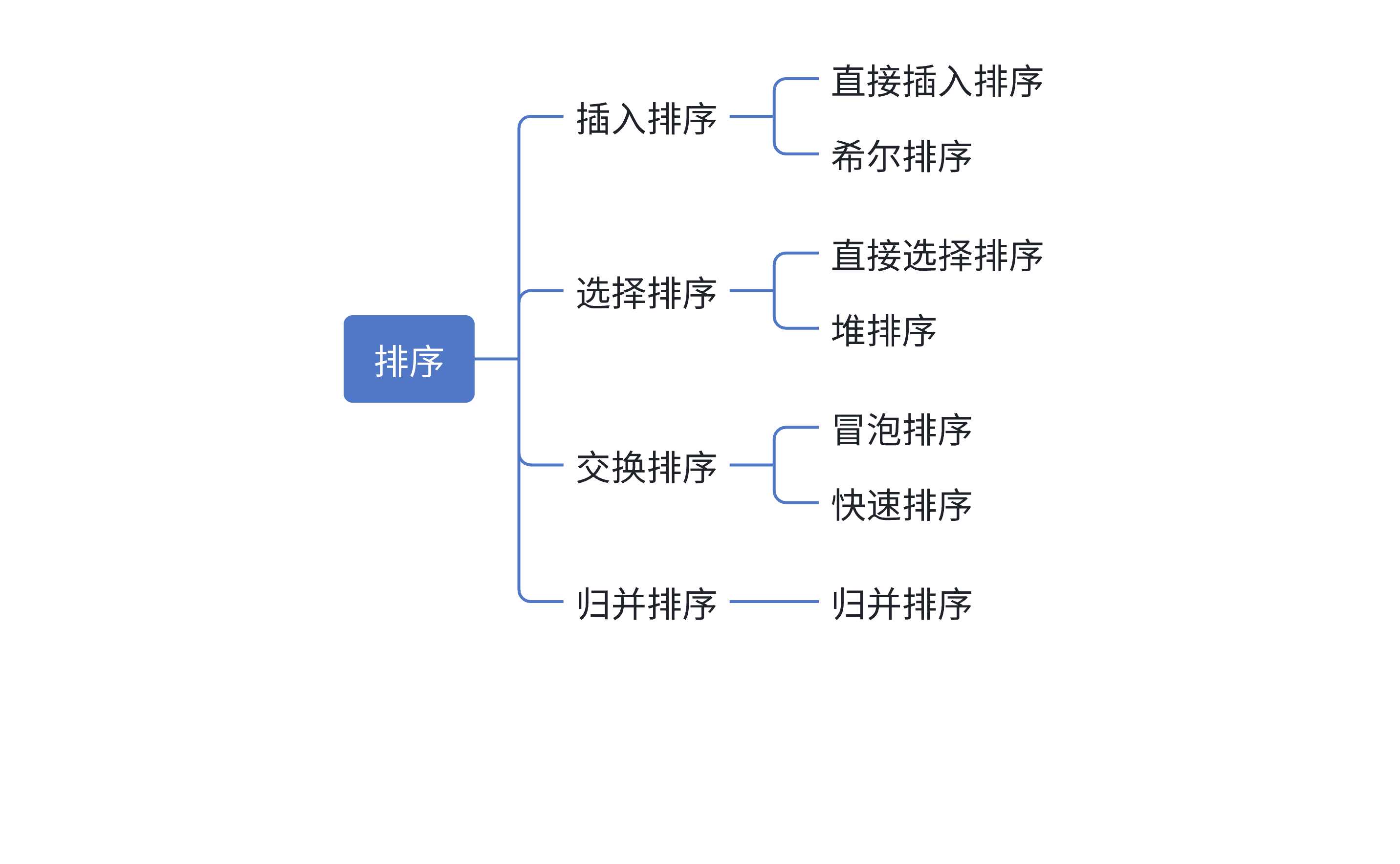
我们常见的排序算法有插入排序、选择排序、交换排序和归并排序等,如下所示:
二、插入排序
插入排序是一种简单直观的排序算法,适用于小规模数据或部分有序的数据集。其核心思想是通过构建有序序列,逐步将未排序的元素插入到已排序部分的正确位置。
实际上,在我们玩扑克牌时,就用到了插入排序的思想。

2.1 直接插入排序
直接插入排序的基本思想是将一个元素插入到已经排好序的部分数组中,从而逐步构建有序序列。
让我们来想象一下玩扑克牌时整理手牌的过程:我们会将每张新牌插入到已有序的手牌中的适当位置。而直接插入排序正是采用了这种思想:
- 从数组的第二个元素开始处理(默认第一个元素已构成有序序列);
- 对于每个待插入元素,与已排序部分的元素从后往前比较;
- 找到合适位置后插入该元素;
- 重复上述过程直到所有元素都被处理。
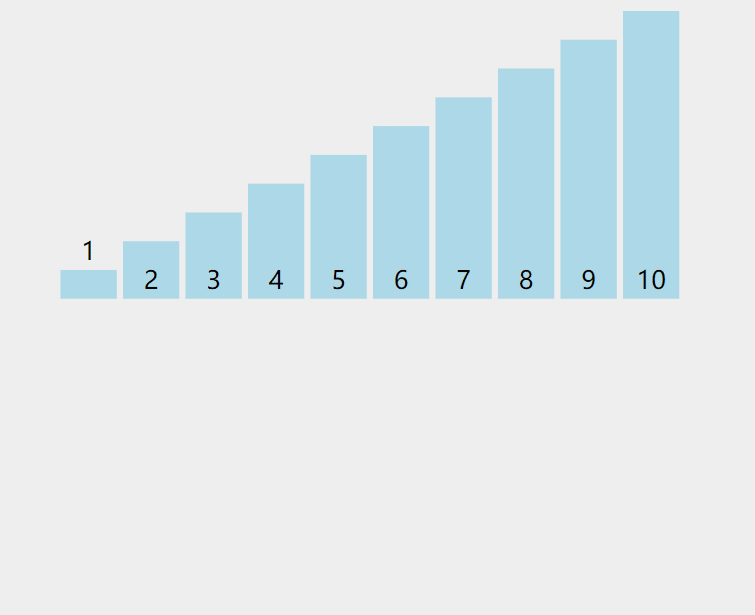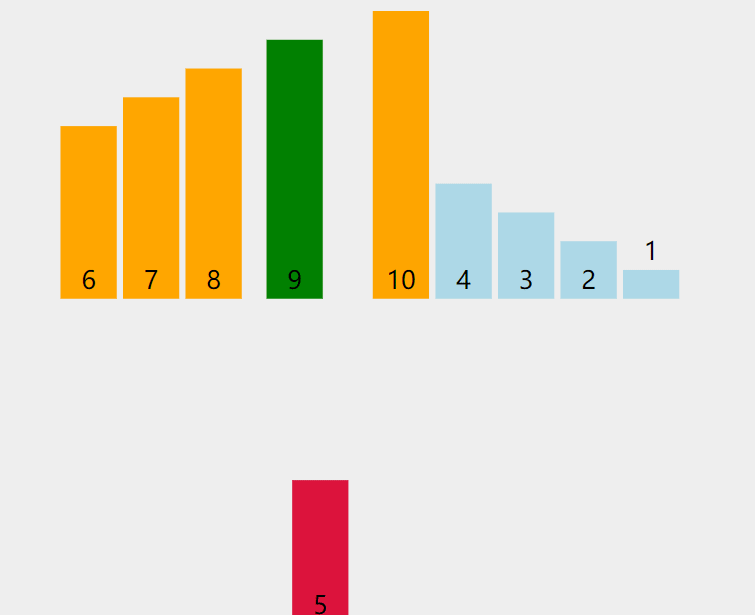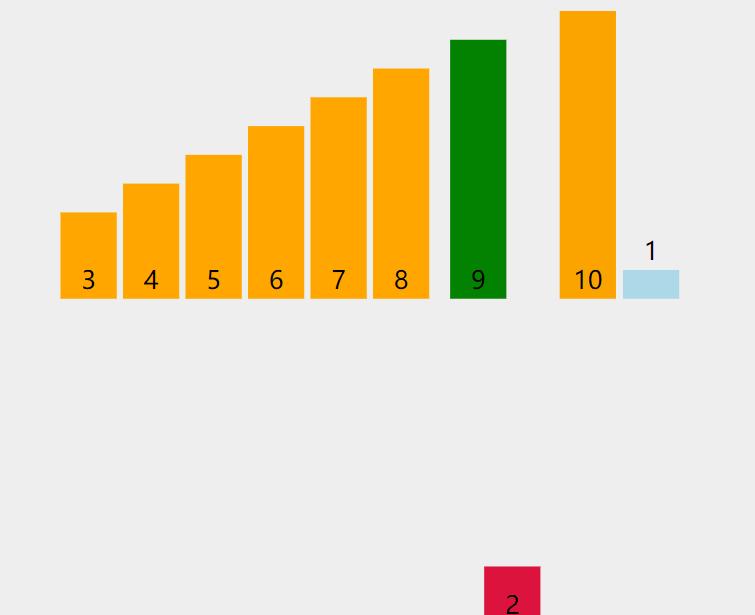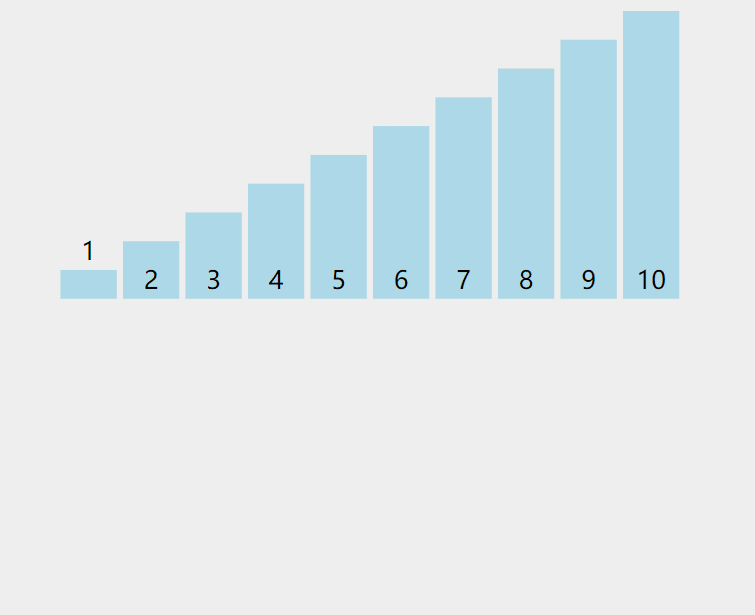
直接插入排序的核心逻辑如下:
- 外层循环:遍历所有待插入的元素(从第二个元素到最后一个);
- 内层循环:将当前元素与已排序部分比较,找到插入位置;
- 插入操作:将元素放入正确位置,同时移动其他元素为其腾出空间。
下面我们来看一下代码实现:
#include <stdio.h>// 直接插入排序函数
void insertionSort(int arr[], int n) {int i, key, j;// 外层循环:从第二个元素开始处理for (i = 1; i < n; i++) {key = arr[i]; // 保存当前待插入的元素j = i - 1; // 从已排序部分的最后一个元素开始比较// 内层循环:找到合适的插入位置// 将大于key的元素向后移动一位while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key; // 插入元素到正确位置}
}应用示例如下:
// 打印数组函数
void printArray(int arr[], int size) {int i;for (i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");
}// 主函数示例
int main() {int arr[] = {12, 11, 13, 5, 6};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前的数组: ");printArray(arr, n);insertionSort(arr, n);printf("排序后的数组: ");printArray(arr, n);return 0;
}输出结果为:
排序前的数组: 12 11 13 5 6
排序后的数组: 5 6 11 12 13 对于直接插入排序的时间复杂度,当数组有序时,时间复杂度情况最佳,只需要进行n-1次比较,此时时间复杂度为;当数组完全逆序的时候,时间复杂度最差,需要进行
次比较和移动,此时时间复杂度为
。
2.2 希尔排序
希尔排序法又叫做缩小增量法,其基本思想在于:先选定一个整数(通常是),把待排序文件所有记录分成各组,所有的距离相等的记录分在同一组内,并对每一组内的记录进行排序,然后
得到下一个整数,再将数组分成各组,进行插入排序。当
时,就相当于是直接插入排序。
希尔排序法是在直接插入排序算法的基础上进行改进而来的,综合来说它的效率是要高于直接插入排序算法的。
希尔排序的核心思想是分组插入排序:
- 选择一个增量序列(通常是 n/2, n/4, ..., 1);
- 对于每个增量,将数组按增量分成若干个子序列;
- 对每个子序列进行直接插入排序;
- 逐步减小增量,重复上述过程;
- 当增量为 1 时,整个数组被视为一个子序列,进行最后一次插入排序。
通过这种方式,元素可以一次性移动较远距离,而不是像普通插入排序那样只能一步一步移动,从而大大提高效率。
画图分析如下:
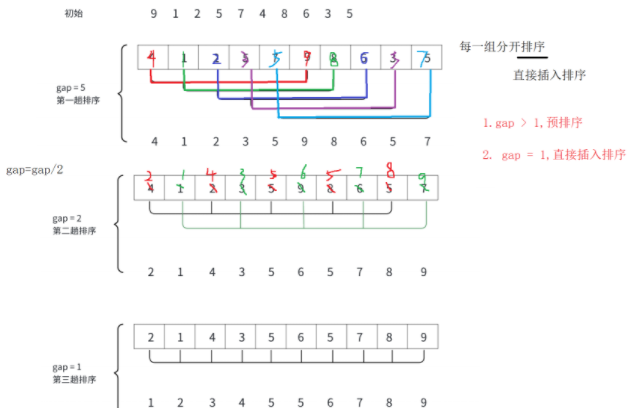
完整代码如下:
#include <stdio.h>// 希尔排序函数
void shellSort(int arr[], int n) {// 初始增量为数组长度的一半,逐渐减小增量for (int gap = n/2; gap > 0; gap /= 2) {// 对每个子序列进行插入排序for (int i = gap; i < n; i++) {int temp = arr[i]; // 保存当前待插入元素// 对子序列中的元素进行比较和移动int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp; // 插入元素到正确位置}}
}应用示例如下:
// 打印数组函数
void printArray(int arr[], int size) {int i;for (i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");
}// 主函数示例
int main() {int arr[] = {12, 34, 54, 2, 3};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前的数组: ");printArray(arr, n);shellSort(arr, n);printf("排序后的数组: ");printArray(arr, n);return 0;
}排序前的数组: 12 34 54 2 3
排序后的数组: 2 3 12 34 54 2.2.1 希尔排序特性总结
1. 希尔排序是对直接插入排序的优化。
2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近于有序了,这样就会很快。整体而言可以达到优化直接插入排序的效果。
2.2.2 希尔排序的时间复杂度计算
外层循环:
外层循环的时间复杂度可以直接给出为:或者
,即
。
内层循环: 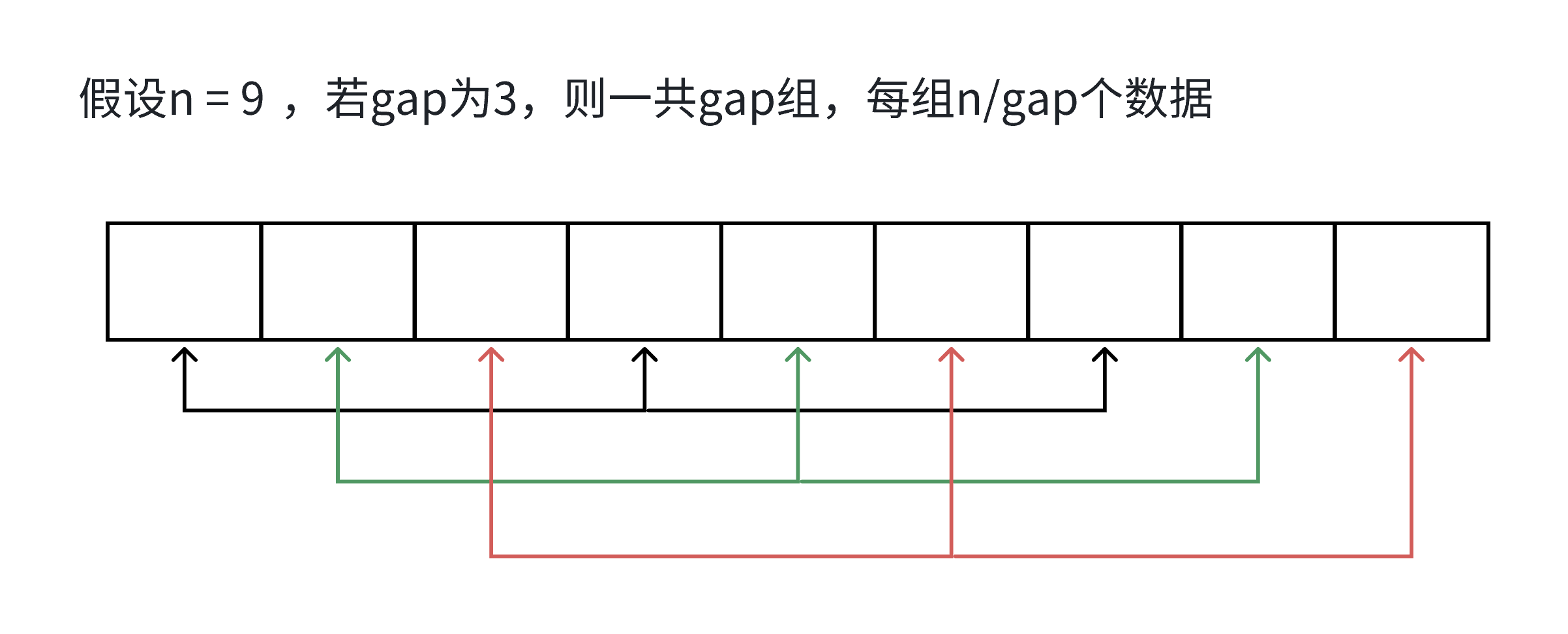
假设一共有n个数据,合计有gap组,则每组为n/gap个。在每组中,插入移动的次数最坏的情况下为,一共是gap组。因此:
总计最坏情况下移动总数为:
gap的取值有(以除3为例):n/3 n/9 n/27 ...... 2 1
- 当gap = n / 3时,移动总数为:
;
- 当gap = n / 9时,移动总数为:
;
- 最后一趟时,gap = 1,即直接插入排序,内层循环排序的消耗为n。
通过上面的分析,我们就可以画出下面这样的曲线图:
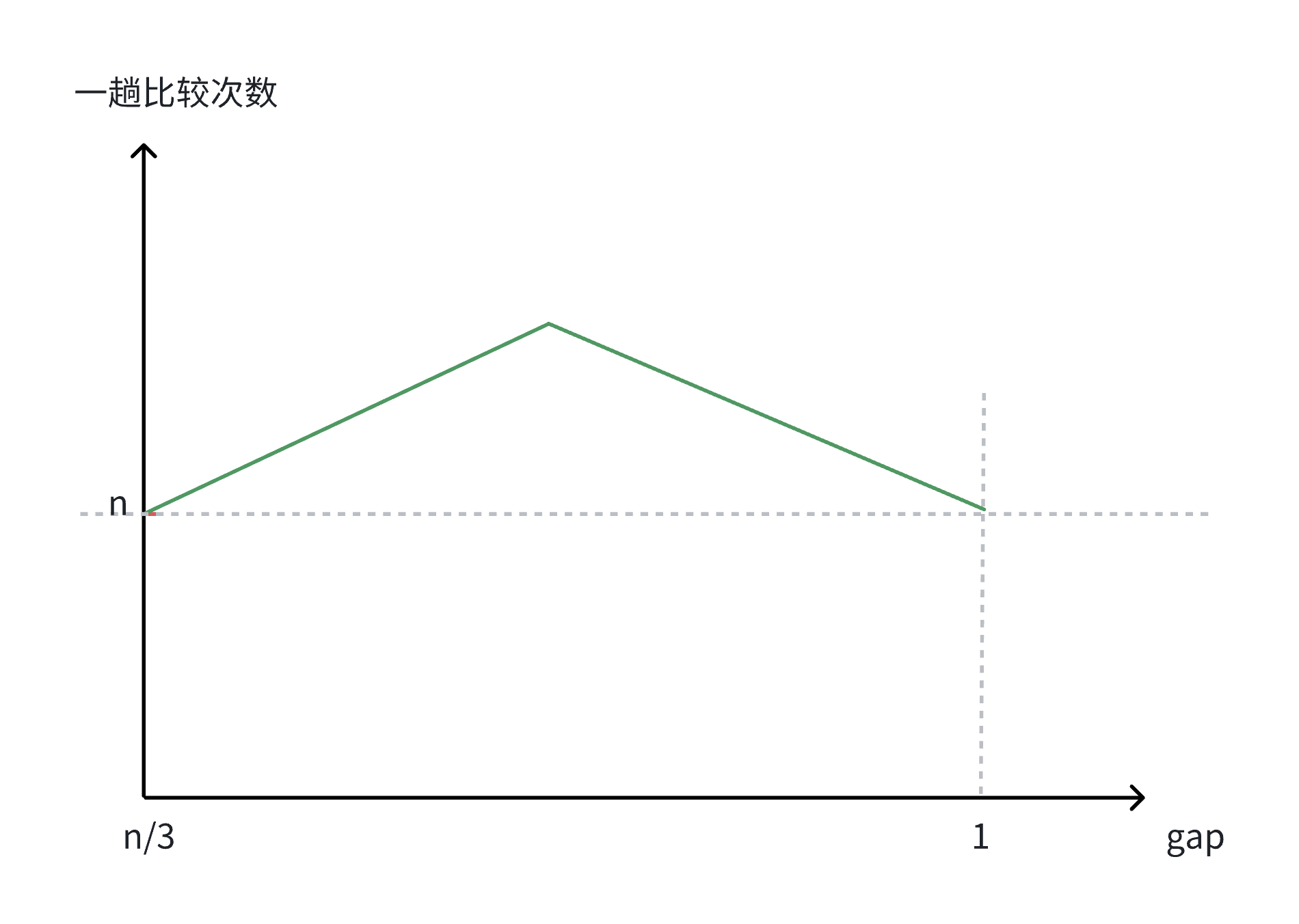
因此,希尔排序在最初和最后的排序的次数都为n,即前一阶段排序次数是逐渐上升的状态,当到达某一顶点的时候,排序次数逐渐下降至n,而该顶点的计算暂时无法给出具体的计算过程。
希尔排序的时间复杂度其实是很难计算的,因为gap的取值有很多,导致计算就变得很困难。因此很多书中给出的希尔排序的时间复杂度都是不太一样的。《数据结构(C语⾔版)》--- 严蔚敏书中给出的时间复杂度为:

总结
本期博客我为大家介绍了插入排序,并介绍了使用希尔排序优化直接插入排序的方法。下期博客我将继续为大家带来排序算法的相关内容,敬请期待!
