当前位置：首页 > news >正文

动态规划解决系列子序列问题

news 2025/9/17 8:07:19

最长递增子序列（LeetCode 300）

摆动序列（LeetCode 376）

最长递增子序列的个数（LeetCode 673）

最长数对链（LeetCode 646）

最长定差子序列（LeetCode 1218）

最长的斐波那契子序列的长度（LeetCode 873）

最长等差数列（LeetCode 1027）

等差数列划分 II - 子序列（LeetCode 446）

总结

在算法领域，子序列相关问题一直是热门且具有挑战性的部分。这类问题往往需要我们在不改变元素相对顺序的前提下，找出满足特定条件的子序列。动态规划作为一种强大的算法思想，非常适合解决这类具有最优子结构和重叠子问题的子序列问题。接下来，我们就来探讨几道经典的子序列问题，看看如何用动态规划来解决它们。

最长递增子序列（LeetCode 300）

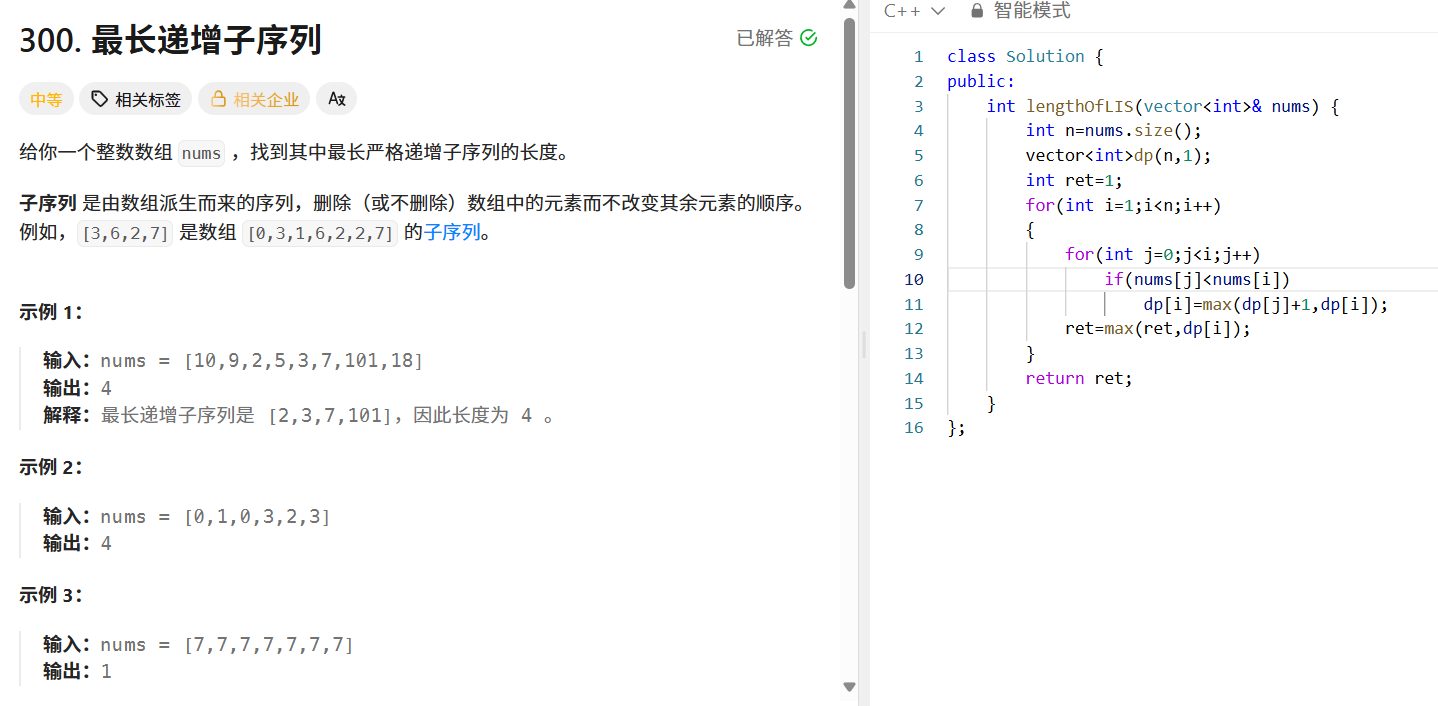
问题分析：给定一个整数数组，要找出其中最长严格递增子序列的长度。子序列是删除数组中部分元素（也可不删）后，剩余元素顺序不变的序列。

动态规划思路：

- 定义 dp[i]  表示以第 i  个元素结尾的最长严格递增子序列的长度。
- 初始时，每个元素自身就是一个长度为 1  的子序列，所以 dp  数组初始化为 1 。
- 对于每个元素 nums[i] ，遍历它之前的所有元素 nums[j] （ j < i ），如果 nums[j] < nums[i] ，说明 nums[i]  可以接在以 nums[j]  结尾的递增子序列后面，此时 dp[i] = max(dp[i[j dp[j] + 1) 。
- 同时维护一个变量 ret ，记录遍历过程中 dp  数组的最大值，即为最长递增子序列的长度。

代码：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = max(dp[i[j dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};

摆动序列（LeetCode 376）

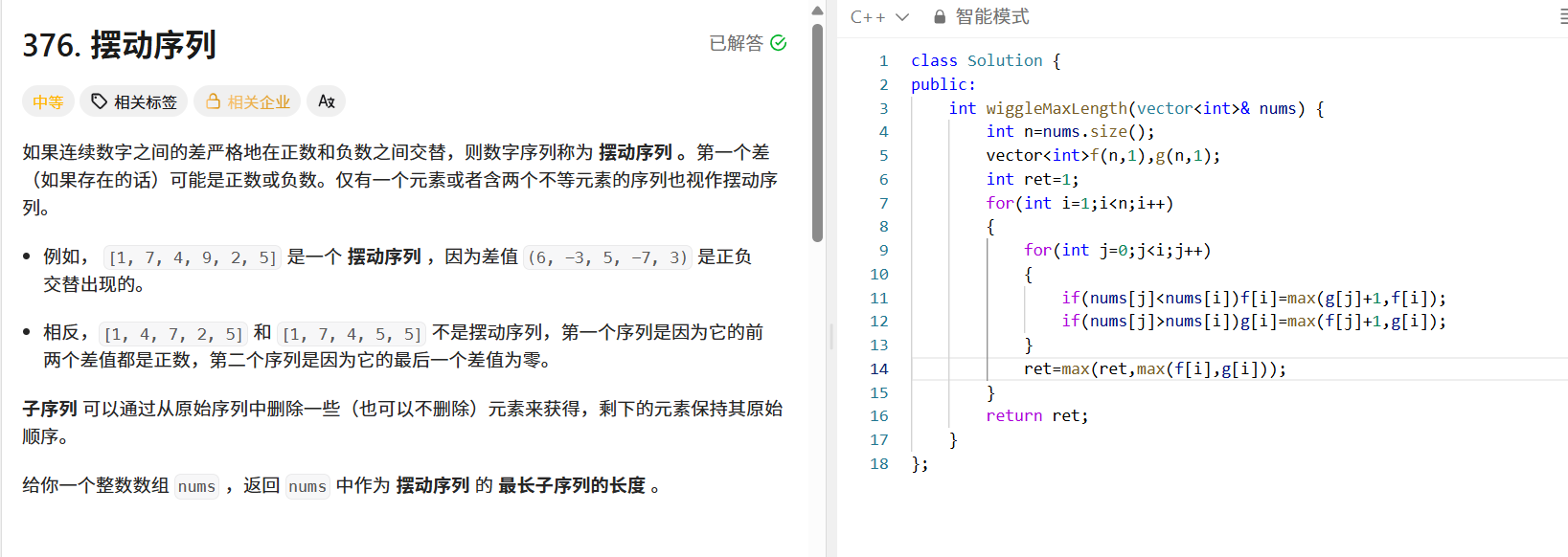
问题分析：如果连续数字之间的差严格在正数和负数之间交替，这样的数字序列就是摆动序列。需要找出最长摆动子序列的长度，子序列通过删除原始序列部分元素（也可不删）得到，剩余元素顺序不变。

动态规划思路：

- 定义 f[i]  表示以第 i  个元素结尾，且最后一个差为正数的最长摆动子序列长度； g[i]  表示以第 i  个元素结尾，且最后一个差为负数的最长摆动子序列长度。
- 初始时， f  和 g  数组都初始化为 1 ，因为单个元素自身就是长度为 1  的摆动序列（符合仅有一个元素的情况）。
- 遍历每个元素 nums[i] ，再遍历它之前的元素 nums[j] （ j < i ）：
- 如果 nums[j] < nums[i] ，说明可以形成最后一个差为正数的摆动序列，此时 f[i] = max(g[j] + 1, f[i]) 。
- 如果 nums[j] > nums[i] ，说明可以形成最后一个差为负数的摆动序列，此时 g[i] = max(f[j] + 1, g[i]) 。
- 维护变量 ret ，记录 f  和 g  数组中的最大值，即为最长摆动子序列的长度。

代码：

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {f[i] = max(g[j] + 1, f[i]);}if (nums[j] > nums[i]) {g[i] = max(f[j] + 1, g[i]);}}ret = max(ret, max(f[i[j g[i]));}return ret;}
};

最长递增子序列的个数（LeetCode 673）

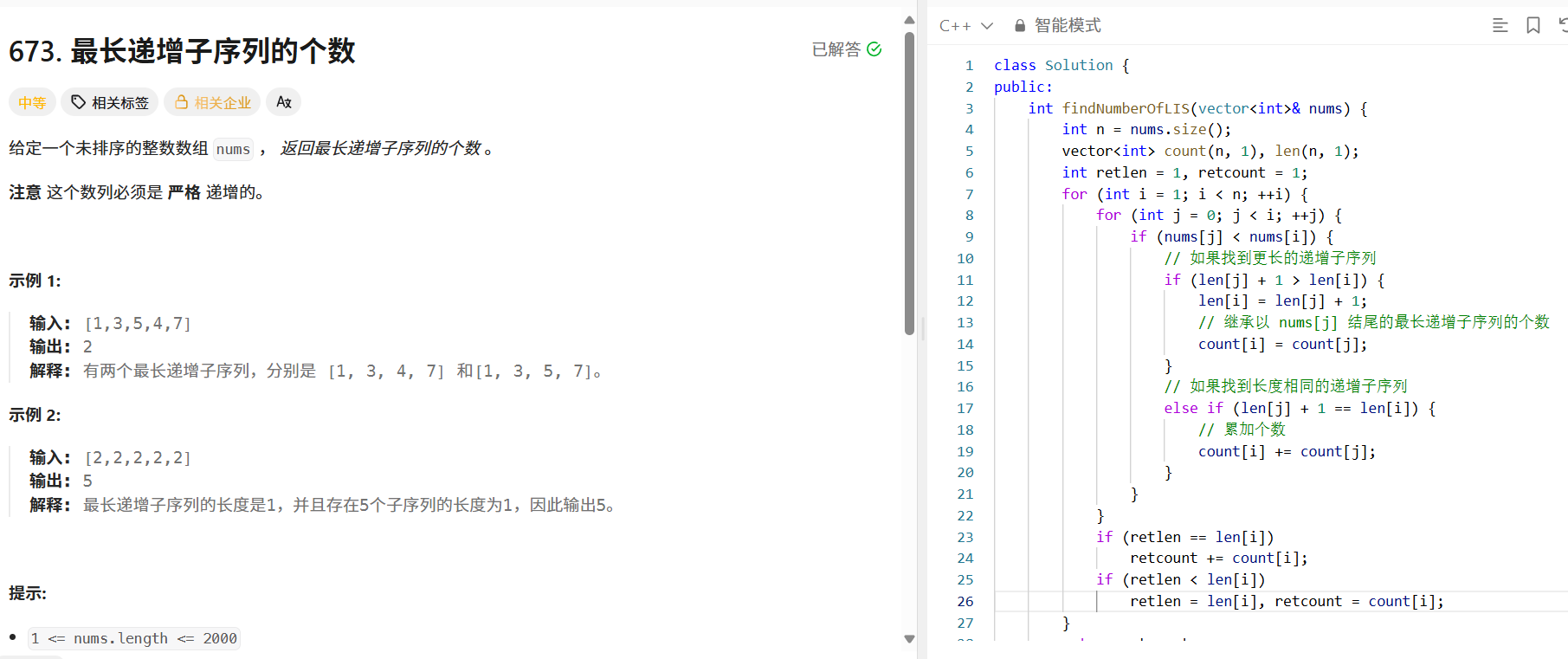
问题分析：给定未排序的整数数组，返回最长递增子序列的个数，要求子序列严格递增。

动态规划思路：

- 定义 len[i]  表示以第 i  个元素结尾的最长递增子序列的长度； count[i]  表示以第 i  个元素结尾的最长递增子序列的个数。
- 初始时， len  和 count  数组都初始化为 1 ，因为每个元素自身是长度为 1  的递增子序列，个数为 1 。
- 遍历每个元素 nums[i] ，再遍历它之前的元素 nums[j] （ j < i ）：
- 如果 nums[j] < nums[i] ：
- 若 len[j] + 1 > len[i] ，说明找到更长的递增子序列，此时 len[i] = len[j] + 1 ，并且 count[i] = count[j] （继承以 nums[j]  结尾的最长递增子序列的个数）。
- 若 len[j] + 1 == len[i] ，说明找到长度相同的递增子序列，此时 count[i] += count[j] （累加个数）。
- 遍历过程中，维护 retlen （最长递增子序列的长度）和 retcount （对应的个数）。若当前 len[i]  大于 retlen ，则更新 retlen  为 len[i] ， retcount  为 count[i] ；若 len[i] == retlen ，则 retcount += count[i] 。

代码：

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> count(n, 1), len(n, 1);int retlen = 1, retcount = 1;for (int i = 1; i < n; ++i) {for (int j = 0; j < i; ++j) {if (nums[j] < nums[i]) {if (len[j] + 1 > len[i]) {len[i] = len[j] + 1;count[i] = count[j];} else if (len[j] + 1 == len[i]) {count[i] += count[j];}}}if (retlen == len[i]) {retcount += count[i];}if (retlen < len[i]) {retlen = len[i];retcount = count[i];}}return retcount;}
};

最长数对链（LeetCode 646）

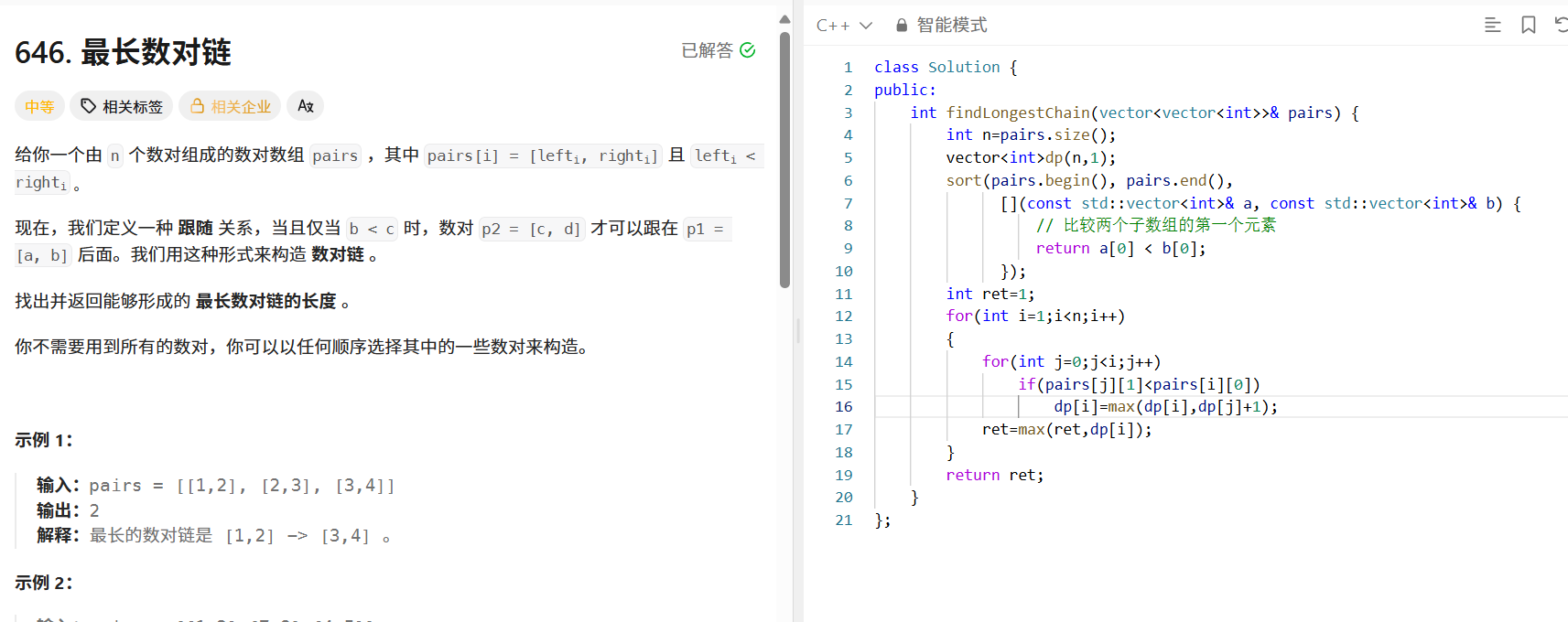
问题分析：给定数对数组，数对 [a,b]  满足 a < b ，定义数对 p2 = [c,d]  可跟在 p1 = [a,b]  后当且仅当 b < c ，要找出最长数对链的长度。

动态规划思路：

- 先对数对数组按照数对的第一个元素进行排序，这样方便后续判断数对之间的跟随关系。
- 定义 dp[i]  表示以第 i  个数对结尾的最长数对链的长度，初始化为 1 ，因为每个数对自身可作为长度为 1  的数对链。
- 遍历每个数对 pairs[i] ，再遍历它之前的数对 pairs[j] （ j < i ），如果 pairs[j][1] < pairs[i][0] ，说明 pairs[i]  可以跟在 pairs[j]  后面，此时 dp[i] = max(dp[i[j dp[j] + 1) 。
- 维护变量 ret ，记录 dp  数组中的最大值，即为最长数对链的长度。

代码：

class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {int n = pairs.size();vector<int> dp(n, 1);sort(pairs.begin(), pairs.end(), [](const vector<int>& a, const vector<int>& b) {return a[0] < b[0];});int ret = 1;for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (pairs[j][1] < pairs[i][0]) {dp[i] = max(dp[i[j dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};

最长定差子序列（LeetCode 1218）

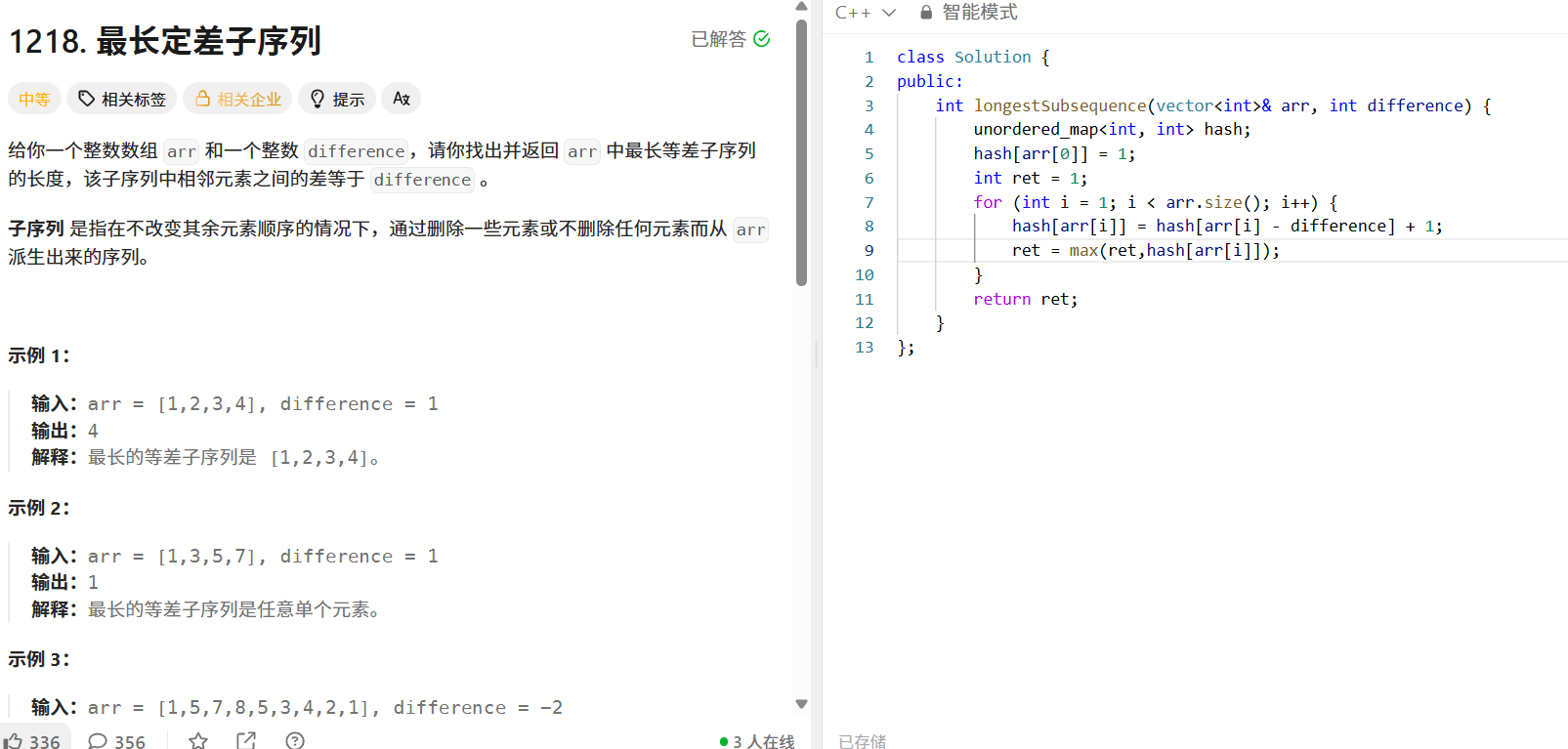
问题分析：给定整数数组和整数 difference ，找出最长等差子序列的长度，子序列中相邻元素差等于 difference 。

动态规划思路：

- 使用哈希表 hash  来记录每个数字对应的最长定差子序列长度。
- 初始时， hash[arr[0]] = 1 ，因为第一个元素自身是长度为 1  的子序列。
- 遍历数组从第二个元素开始，对于当前元素 arr[i] ，计算 arr[i] - difference ，如果该值在哈希表中存在，说明 arr[i]  可以接在以 arr[i] - difference  结尾的定差子序列后面，此时 hash[arr[i]] = hash[arr[i] - difference] + 1 ；否则， hash[arr[i]] = 1 （自身作为长度为 1  的子序列）。
- 维护变量 ret ，记录哈希表中的最大值，即为最长定差子序列的长度。

代码：

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;hash[arr[0]] = 1;int ret = 1;for (int i = 1; i < arr.size(); i++) {hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};

最长的斐波那契子序列的长度（LeetCode 873）

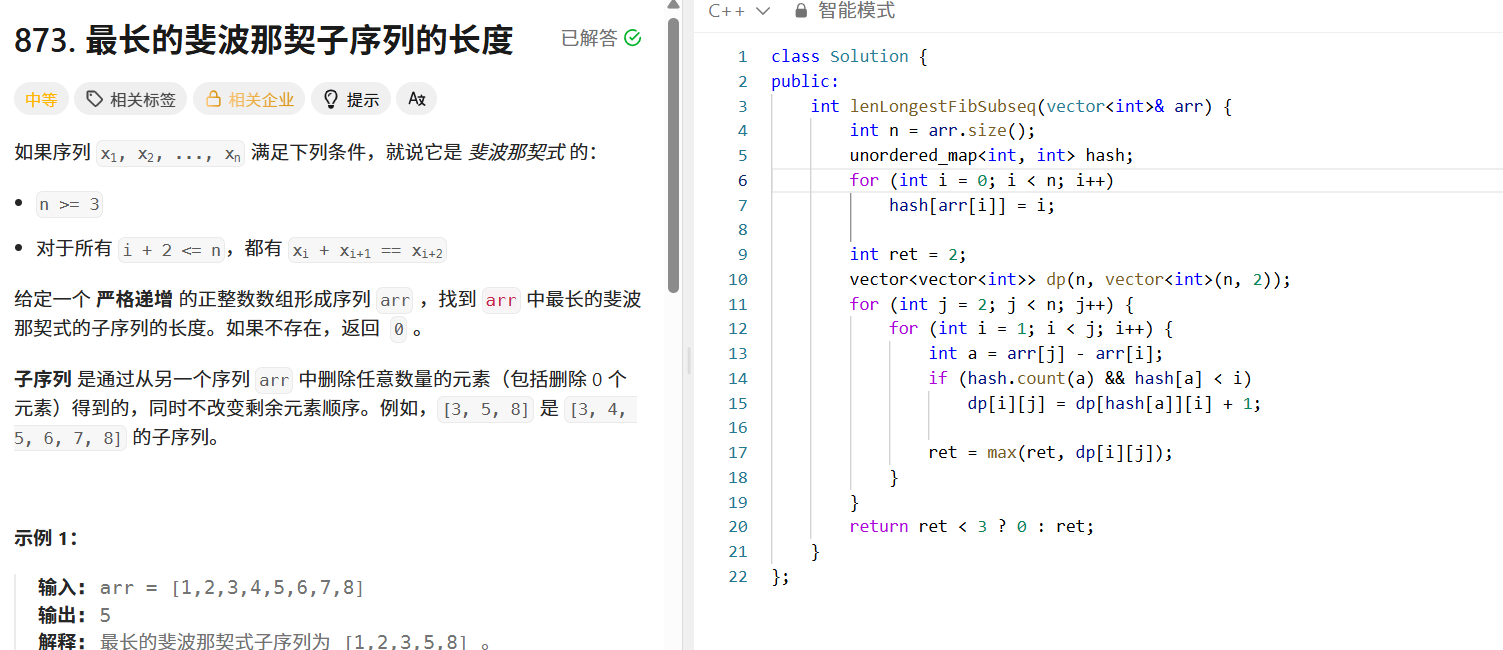
问题分析：斐波那契式序列满足 n >= 3  且对于所有 i + 2 <= n ，有 x_i + x_{i+1} = x_{i+2} 。给定严格递增的正整数数组，找出最长斐波那契式子序列的长度，不存在则返回 0 。

动态规划思路：

- 首先用哈希表 hash  记录每个数字在数组中的索引，方便快速查找。
- 定义二维数组 dp ，其中 dp[i][j]  表示以第 i  个和第 j  个元素结尾的斐波那契子序列的长度。初始时， dp  数组每个元素初始化为 2 ，因为两个元素自身还不能构成斐波那契序列（需要至少三个元素）。
- 遍历数组，对于每个 j （从 2  开始），再遍历每个 i （从 1  开始，且 i < j ），计算 a = arr[j] - arr[i] 。如果 a  在哈希表中且其索引小于 i ，说明存在 a  使得 a, arr[i], arr],]  构成斐波那契序列的前三个元素，此时 dp[i][j] = dp[hash[a]][i] + 1 。
- 维护变量 ret ，记录 dp  数组中的最大值。最后如果 ret < 3 ，说明不存在符合要求的斐波那契子序列，返回 0 ，否则返回 ret 。

代码：

class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();unordered_map<int, int> hash;for (int i = 0; i < n; i++) {hash[arr[i]] = i;}int ret = 2;vector<vector<int>> dp(n, vector<int>(n, 2));for (int j = 2; j < n; j++) {for (int i = 1; i < j; i++) {int a = arr[j] - arr[i];if (hash.count(a) && hash[a] < i) {dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}}return ret < 3 ? 0 : ret;}
};

最长等差数列（LeetCode 1027）

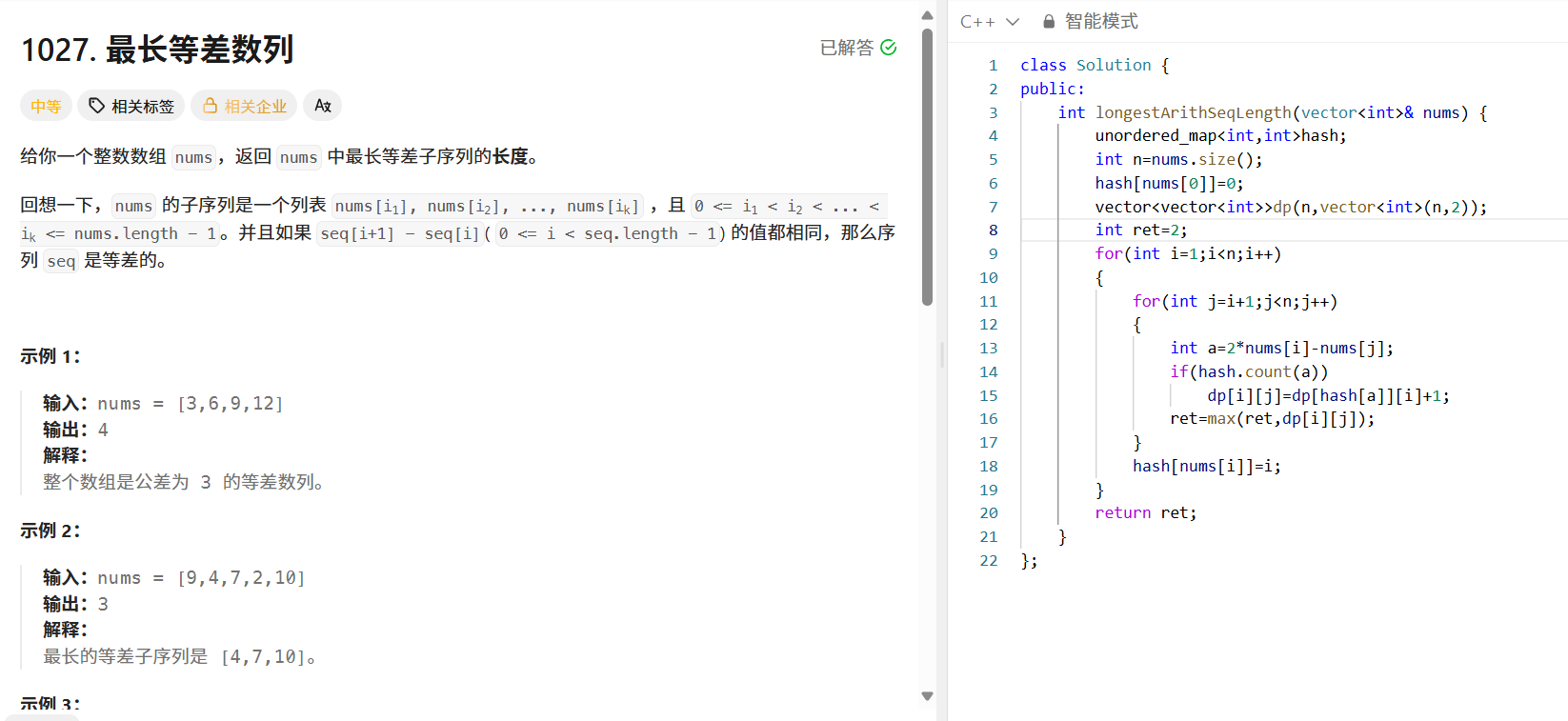
问题分析：返回数组中最长等差子序列的长度，等差子序列要求子序列中相邻元素差相同。

动态规划思路：

- 用哈希表 hash  记录每个数字在数组中的索引，方便查找。
- 定义二维数组 dp ，其中 dp[i][j]  表示以第 i  个和第 j  个元素结尾的等差子序列的长度。初始时， dp  数组每个元素初始化为 2 ，因为两个元素可作为长度为 2  的等差子序列（差为两数之差）。
- 遍历数组，对于每个 i （从 1  开始），再遍历每个 j （从 i+1  开始），计算 a = 2 * nums[i] - nums[j] 。如果 a  在哈希表中，说明存在 a  使得 a, nums[i[j nums[j]  构成等差序列的前三个元素，此时 dp[i][j] = dp[hash[a]][i] + 1 。
- 维护变量 ret ，记录 dp  数组中的最大值，即为最长等差子序列的长度。

代码：

class Solution {
public:int longestArithSeqLength(vector<int>& nums) {unordered_map<int, int> hash;int n = nums.size();hash[nums[0]] = 0;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int i = 1; i < n; i++) {for (int j = i + 1; j < n; j++) {int a = 2 * nums[i] - nums[j];if (hash.count(a)) {dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;}
};

等差数列划分 II - 子序列（LeetCode 446）

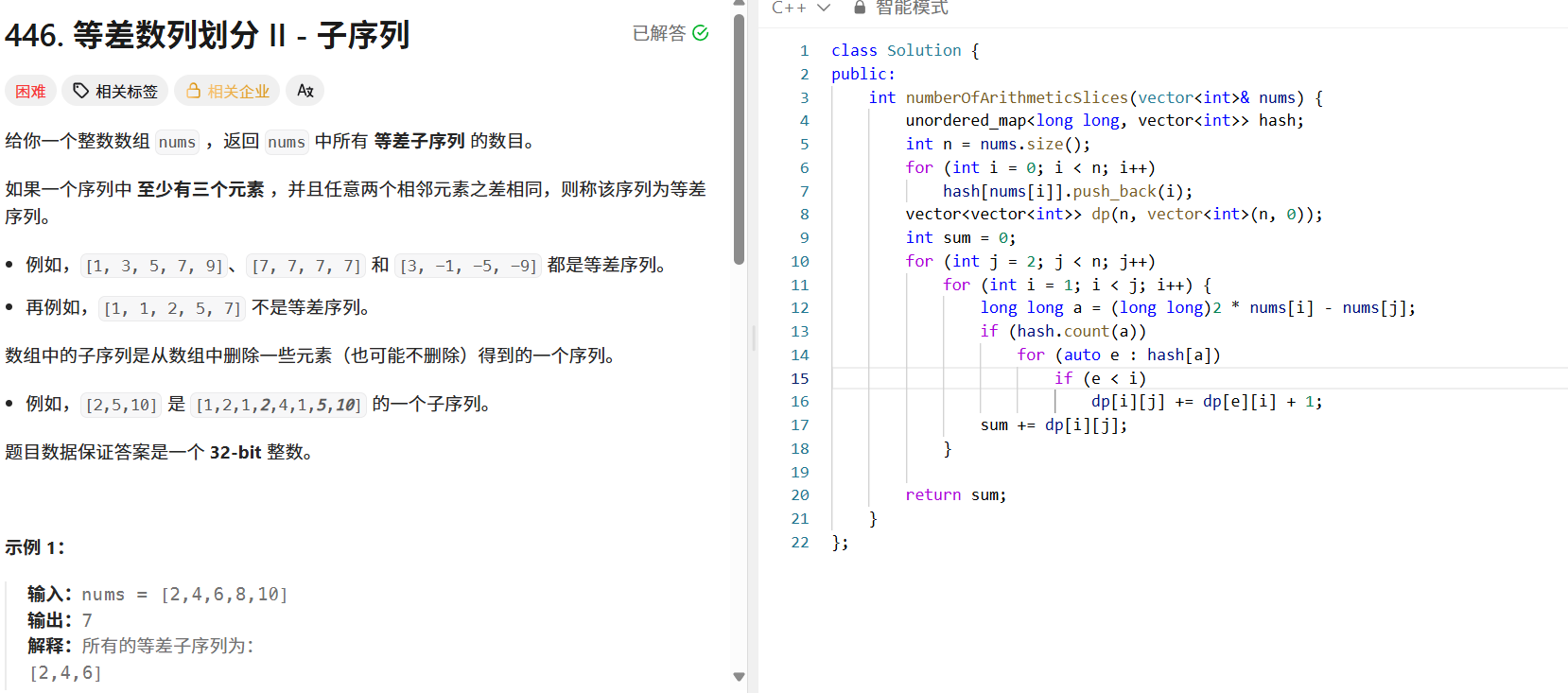
问题分析：返回数组中所有等差子序列的数目，等差子序列要求至少有三个元素且相邻元素差相同。

动态规划思路：

- 用哈希表 hash  记录每个数字对应的索引列表，方便查找相同数字的位置。
- 定义二维数组 dp ，其中 dp[i][j]  表示以第 i  个和第 j  个元素结尾的等差子序列的数目（长度至少为 3 ）。
- 遍历数组，对于每个 j （从 2  开始），再遍历每个 i （从 1  开始，且 i < j ），计算 a = (long long)2 * nums[i] - nums[j] 。如果 a  在哈希表中，遍历 a  对应的所有索引 e （且 e < i ），此时 dp[i][j] += dp[e][i] + 1 （ dp[e][i]  是之前以 e  和 i  结尾的等差子序列数目， +1  是因为 e, i, j  构成新的等差子序列）。
- 维护变量 sum ，累加所有 dp[i][j]  的值，即为所有等差子序列的数目。

代码：

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {unordered_map<long long, vector<int>> hash;int n = nums.size();for (int i = 0; i < n; i++) {hash[nums[i]].push_back(i);}vector<vector<int>> dp(n, vector<int>(n, 0));int sum = 0;for (int j = 2; j < n; j++) {for (int i = 1; i < j; i++) {long long a = (long long)2 * nums[i] - nums[j];if (hash.count(a)) {for (auto e : hash[a]) {if (e < i) {dp[i][j] += dp[e][i] + 1;}}}sum += dp[i][j];}}return sum;}
};