当前位置：首页 > news >正文

机器人导论第六章动力学（2）——拉格朗日动力学推导与详述

news 2025/9/17 7:58:45

在https://blog.csdn.net/2301_80226956/article/details/147035633?spm=1001.2014.3001.5502
这篇文章已经“抽象”地推导了如上方程，文中的形式是：

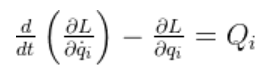
具体推导会涉及虚功原理，因此不严谨推导，上文仅供理解。

动力学的目的就是：

给定机器人的关节位置 q、速度 qd 和加速度 qdd，计算出为了产生这个运动状态，每个关节需要施加多大的驱动力矩 。

力域雅可比与动力学的混淆问题

一上来看到有人问——我们不是用力域雅可比解决了每个关节应该分配多大力矩的问题了吗？

这是我初学的时候也弄混的问题。

“力域雅可比”解决的是一个不同的问题，属于静力学或外力映射范畴，他的目的是将作用在机器人末端执行器上的外力/力矩映射到对应的关节空间力矩。

区别就是一个是给定运动状态，计算每个关节为了达到这个运动状态需要多大力；
另一个则是给定末端的力，计算这个力分配在各个关节上是多大。

前言

拉格朗日动力学方程和之前讲的牛顿-欧拉迭代法都是用于解决动力学问题的思路，但二者有本质区别，牛顿欧拉方程的观点是力平衡下的推导，而拉格朗日法则是基于最低能量原理的推导，具体来说，就是物体总是倾向走能量消耗最小的轨迹。

书上只给出了RP机构的推导，但实际应用上更多时候是串联的旋转关节机械臂，因此本文参考 UP：德狗追求独立的视频【机器人动力学拉格朗日法详细推导(二连杆机械臂)】 https://www.bilibili.com/video/BV1DP4y1o7Bu/?share_source=copy_web&vd_source=2c56c6a2645587b49d62e5b12b253dca

拉格朗日动力学方程的推导

对二连杆机械臂进行拉格朗日动力学分析，这种分析可以扩展到任意关节的串联机械臂。

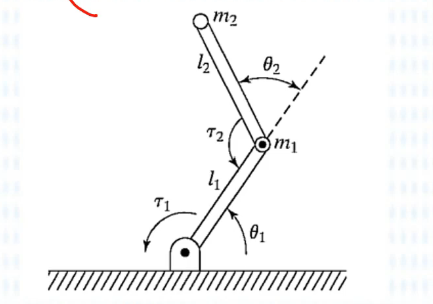
我们的核心就是计算右侧的τ，因此就必须计算左侧的各参数，分别是：
$k$ ——动能：由角动能和线动能组成
$u$ ——势能
$\Theta$ ——关节角度
$\tau$ ——各关节力矩

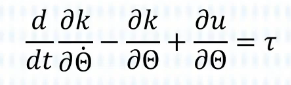
对于上面的二连杆机械臂，我们做出简化：
假设质量都集中在连杆末端，这样能大大简化关于角量的计算，因此此时惯量矩阵为0；

动能 k 计算

首先计算动能k1k2，其中第一项是线动能，第二项是角动能，而由于我们的简化，第二项置零。

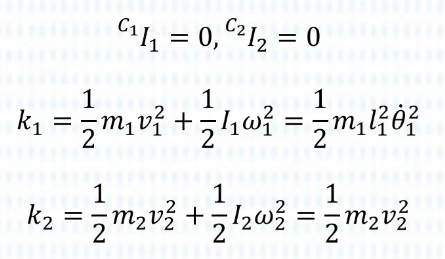
对于第一连杆， $v_1=\omega_1 \cdot r_1$ ，因此动能很容易得到：
$k_1 = \frac{1}{2} m_1 l_1^2 \dot{\theta}_1^2$

对于第二连杆，由于涉及速度牵连，如果多连杆，那么计算的复杂度一定很大，因此我们引入广义坐标和广义速度计算。

通过对广义坐标x2,y2求导就能得到第二连杆在xy方向的分速度，接着合成速度即可。

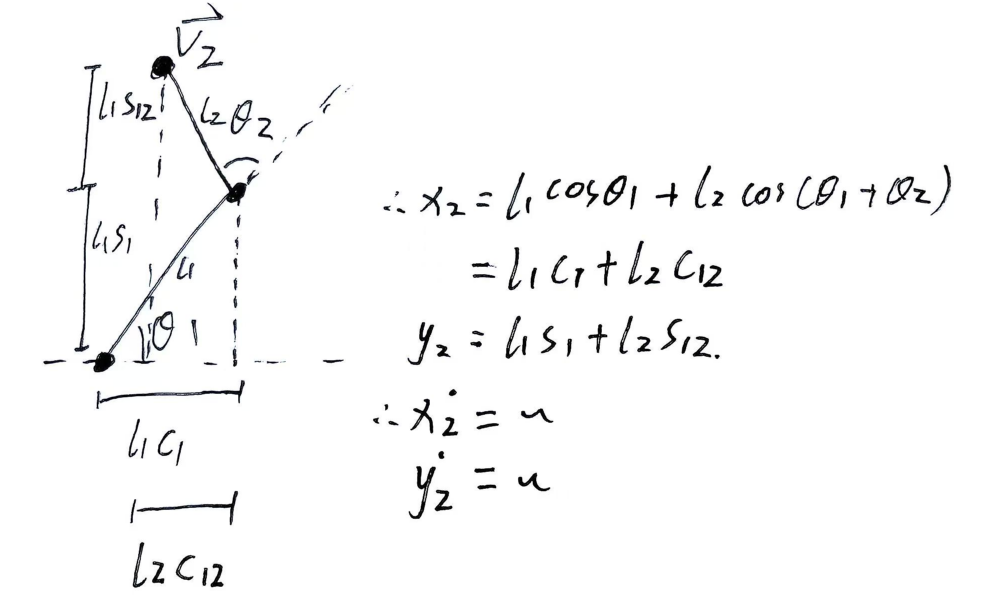
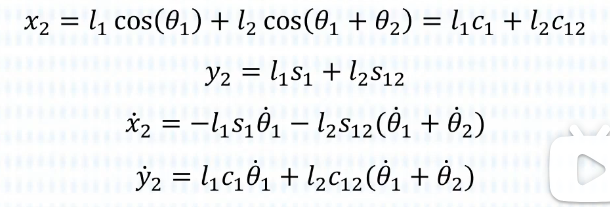
合成分速度：

$k_1 = \frac{1}{2} m_1 l_1^2 \dot{\theta}_1^2$

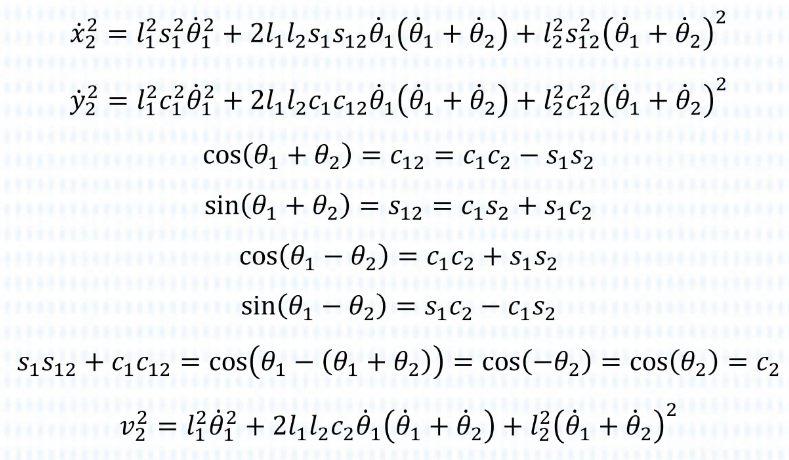
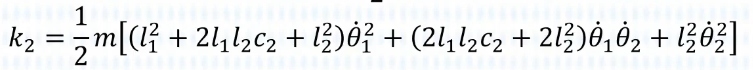
因此总动能：

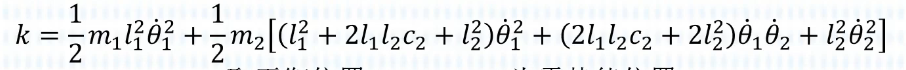
势能 u 计算

u=mgh，h用这种投影到y轴上即可。

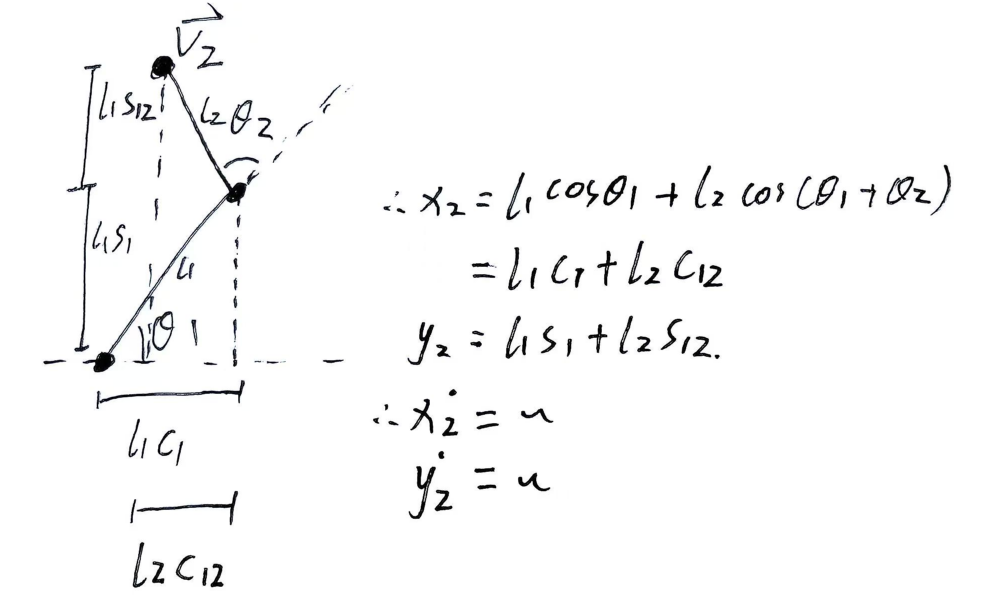
关节力矩 τ 计算

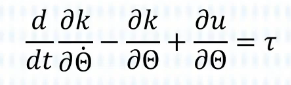
现在ku都算出来了，接下来就要完成整个左式的计算。

求导法则别忘咯：链式法则、嵌套函数的求导：外导乘内导、乘积求导法则：导原原导

首先计算 $\frac{\partial u}{\partial\Theta}$ ：

请注意，求导是“分别”对每个关节求导，因此每次都只需要求对 $\theta_i$ 的导数，一会列式子也是每个关节满足自身的方程。

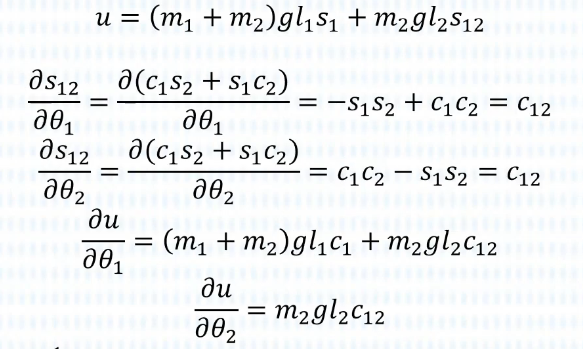
接着求 $\frac{\partial k}{\partial \Theta}$ ：

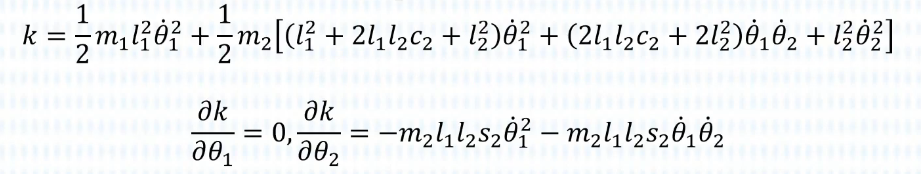
最后求 $\frac{d}{dt}\frac{\partial k}{\partial \Theta}$ ：

注意这里是对时间求导，不是对关节变量求导！

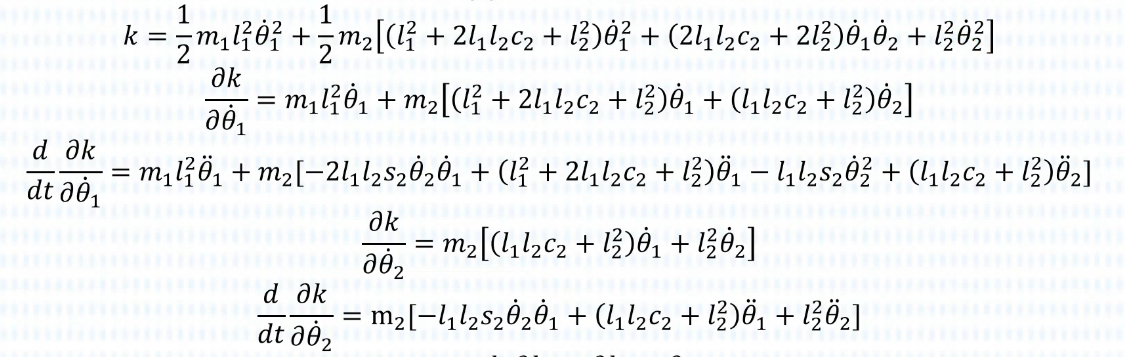
经过上面推导，我们能得到：

$\frac{\partial u}{\partial\theta_1}$ $\frac{\partial u}{\partial\theta_2}$
$\frac{\partial k}{\partial \theta_1}$ $\frac{\partial k}{\partial \theta_2}$
$\frac{d}{dt}\frac{\partial k}{\partial \theta_1}$ $\frac{d}{dt}\frac{\partial k}{\partial \theta_2}$

他们分别是：

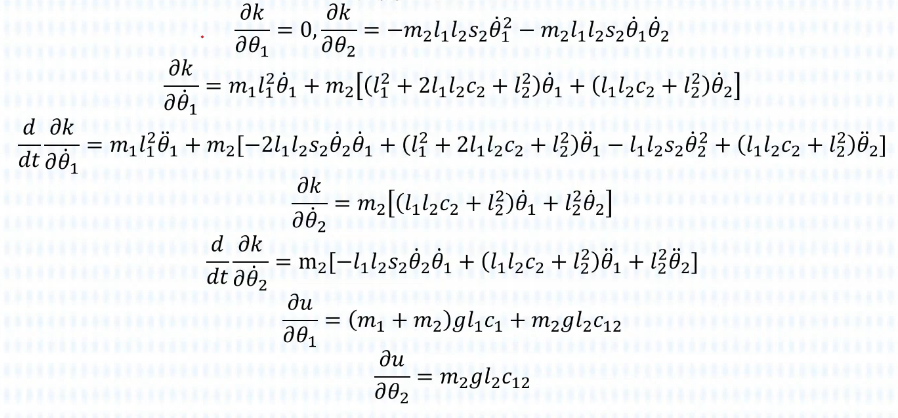
这样，我们就可以计算关节力矩τ了！
把上述六个变量带入：

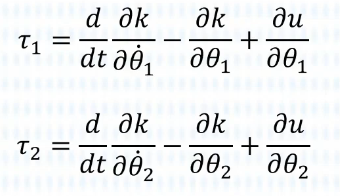
计算得到：

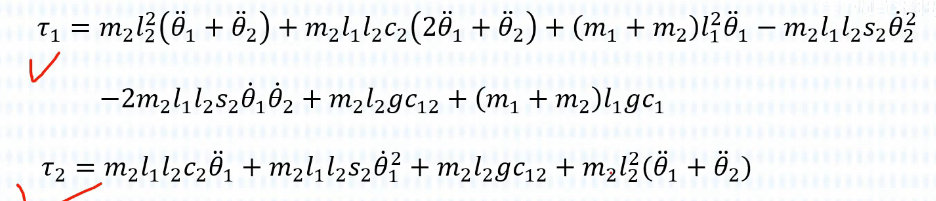
整理为状态空间方程

为什么

这个形式不美观，我们往往会整理为状态空间方程，即，可以通过对关节变量次数的不同，可以整理为 $M(\Theta)$ 质量矩阵， $V(\Theta, \dot \Theta)$ 离心力和哥氏力， $G(\Theta)$ 重力矢量。

这是因为：
关节力矩一受牛顿力学影响—— $F=M(\Theta)\ddot \Theta$ ，这部分反映了系统的惯性特性，他只与加速度有关，于是力矩τ的式子包含 $\ddot \Theta$ 的项就被整理进 $M(\Theta)$ 中了。

二受离心力和哥氏力影响—— $V(\Theta, \dot \Theta)$ ，离心力和哥氏力都是由于旋转运动产生的惯性力，它们与关节的位置 Θ 和速度 $\dot \Theta$ 有关，于是力矩τ的式子包含Θ、 $\dot \Theta$ 的项就被整理进 $V(\Theta, \dot \Theta)$ 中了。

三要抵消重力影响—— $G(\Theta)$ ，而重力只与势能有关，因此是关于关节变量的普通函数，于是力矩τ的式子仅包含Θ的项就被整理进 $G(\Theta)$ 中了。

哥氏力和离心力的作用

离心力：当一个物体绕着某个轴旋转时，会产生向外的力，这就是离心力。在机器人操作臂中，每个连杆的旋转都会产生离心力，这些力会对相邻的连杆和关节产生作用，从而影响关节力矩。
哥氏力：当一个物体在一个旋转参考系中进行直线运动时，会感受到一个与运动方向垂直的力，这就是哥氏力。在机器人操作臂中，如果一个关节在旋转的同时另一个关节也在运动，那么就会产生哥氏力，这种力同样会影响关节力矩。

由此，可以整理出最后的状态矩阵：

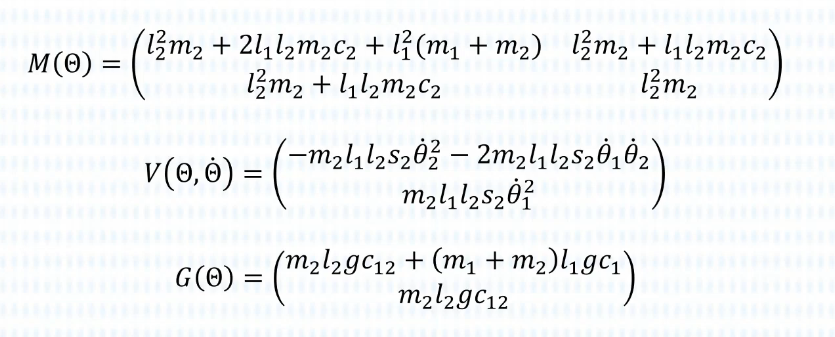
我们再回看状态空间方程：

$\tau = M(\Theta)\ddot{\Theta} + V(\Theta, \dot{\Theta}) + G(\Theta)$

显然，他们都是与关节变量、速度、加速度有关的，因此得到运动状态参数后就能写出上面这些矩阵，并构建方程，从而计算关节力矩了。

对于多连杆串联机械臂

同样的，对于多个连杆的串联机械臂，我们也可以通过获取运动状态参数，从而填充矩阵，计算得出各个关节所需要的力矩，从而驱动关节。

由此，我们就完成了动力学的任务：

给定机器人的关节位置 q、速度 qd 和加速度 qdd，计算出为了产生这个运动状态，每个关节需要施加多大的驱动力矩 。

写在后面

同时我们强调，在真正进行计算的时候用的还是牛顿-欧拉法，因为在复杂度上他有绝对的优势，但做分析的时候，拉格朗日法能提供另一个维度的考量。

为什么选择牛顿欧拉法？

时间复杂度最低——仅O(n)

相对而言，拉格朗日法接近O(n^3)

方法	原理	计算效率
牛顿-欧拉法	牛顿第二定律 + 欧拉方程	⭐⭐⭐⭐⭐ O(n)
拉格朗日法	能量法	⭐⭐ O(n³)
高斯法	最小约束原理	⭐⭐
凯恩法	广义达朗贝尔原理	⭐⭐⭐