[数据结构——Lesson13.冒泡与选择排序]
目录
前言
学习目标
1.冒泡排序
1.1算法思想
1.2算法步骤
循序渐进的双层循环
①首先我们从内层循环开始,将最大的一个数冒到最后
②说完内层循环,接下去来说说套在外层的循环
③冒泡排序优化
2选择排序
2.1算法思想
2.2算法步骤
2.3选择排序时间复杂度分析
结束语:
前言
在上节内容中我们学习了直接插入排序[数据结构——Lesson11排序的概念及直接插入排序]与希尔排序数据结构——lesson12.希尔排序,接下来我们将学习两种新的排序算法——冒泡与选择排序。
学习目标
- 冒泡排序
- 选择排序
1.冒泡排序
1.1算法思想
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行的,直到没有再需要交换的元素为止,这意味着数列已经排序完成。
这个算法的名字由来是因为越小(或越大)的元素会经由交换慢慢“浮”到数列的顶端(或底部)。
1.2算法步骤
1.比较相邻的元素。如果第一个比第二个大(或小,根据排序顺序要求),就交换它们两个。
2.对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数(或最小的数)。
3.针对所有的元素重复以上的步骤,除了已完成排序元素。
4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
注意:如果一轮之后,元素并没有发生任何交换,此时说明此时排序已经完成,那么我们可以提前结束循环。
我们来看个动图就能很直观的理解什么是冒泡排序:
循序渐进的双层循环
- 冒泡排序大家是很熟,但你是不是总有一个困惑,就是这个边界值老是处理不对,内层循环到底是从0开始还是1开始呢,到n - i结束还是n - i - 1结束呢?,这一小节,就带大家从零开始慢慢地实现冒泡排序,了解其循环的开始和终止条件
①首先我们从内层循环开始,将最大的一个数冒到最后
//先写一个单趟的内部排序
for (int j = 1; j < n; ++j)
{if (arr[j - 1] > arr[j]){swap(arr[j - 1], arr[j]);}
}
- 可以看到,这个内部的循环是从1开始到n - 1结束,也就是要比较n次,因此下面可以写成arr[j - 1] > arr[j],但如果你想从0开始也是可以的,那就要到n - 1结束,否则的话比较到最后数组就会越界了
- 若是前一个数比后一个数大,那么就交换它们的位置
②说完内层循环,接下去来说说套在外层的循环
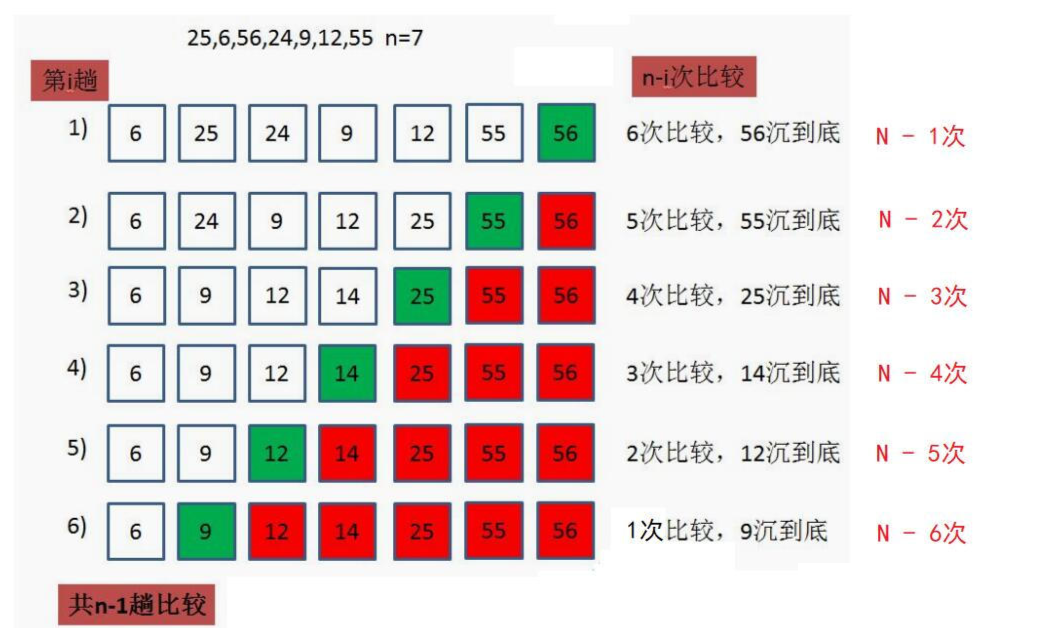
- 从图中可以看到,第一次比较,冒到最后一个位置是n次,而到倒数第二个位置是N- 1次,第二次是N - 2此,依次类推,排序就会进行n - i此的比较,于是我们就可以写出如下代码
for (int i = 0; i < n - 1; i++)
{//先写一个单趟的内部排序for (int j = 1; j < n - i; ++j){if (arr[j - 1] > arr[j]){swap(arr[j - 1], arr[j]);}}PrintArray(arr, n);
}
小结:
- 外层for循环控制的是循环的次数
- 内层for循环控制地是交换的次数
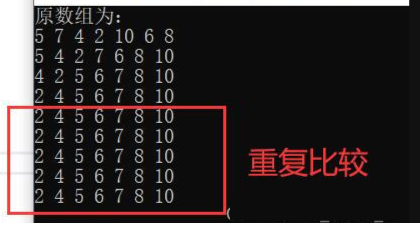
运行结果如下
③冒泡排序优化
了解了边界如何去计算,但是从上图我们可以看出,其实这个数字在进行了四次排序后就已经结束了,完成了升序排序,但是因为外部的循环还没有到末尾,因此还会进行一个继续的比较,我们来将其优化一下吧👈
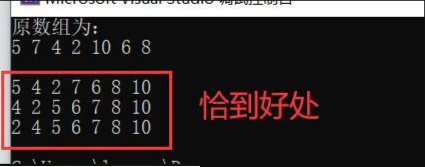
- 首先要定义一个exchanged变量,将其初始化为0,然后在内部循环里判断其是否发生了变化,若是,则将其值置为1,接着在内部循环结束后取判断,看内层循环是否发生了交换,若没有发生交换,则表示此时的数组已经是有序的了,则直接break跳出循环即可
代码
for (int i = 0; i < n - 1; i++)
{int exchanged = 0;//先写一个单趟的内部排序for (int j = 0; j < n - i - 1; ++j){if (arr[j] > arr[j + 1]){swap(arr[j], arr[j + 1]);exchanged = 1;}//PrintArray(arr, n);}/*优化,若是已经有序,则跳出循环*/if (!exchanged) break; PrintArray(arr, n);
}
运行结果
1.3复杂度分析
时间复杂度:最坏情况是数组完全逆序,此时每一轮都需要进行 n - 1 次比较,并且每一轮都会进行至少一次交换.因此,总的比较次数和交换次数都接近 n (n - 1) / 2,其中 n 是数组的长度。所以,最坏情况下的时间复杂度是 O(n ^ 2) 。
空间复杂度:由于没有开辟额外的空间大小,因此空间复杂度为O(1)
2选择排序
2.1算法思想
选择排序(Selection Sort)是一种简单直观的排序算法。通过不断选择剩余元素之中的最小(或最大)元素,然后与起始位置的元素交换(起始位置在每一次选择后都向后移动一位),直到整个序列排序完成。
2.2算法步骤
1.在未排序序列中找到最小(大)元素。遍历未排序的数组,找到最小(或最大)的元素。
2.存放到排序序列的起始位置。将找到的最小(或最大)元素与未排序序列的第一个元素交换位置(如果第一个元素就是最小(大)元素,则它自己和自己交换)。
3.从剩余未排序元素中继续寻找:在剩下的未排序元素中继续执行步骤1和步骤2,直到所有元素都被排序。时间复杂度为O(N2)
void SelectSort(int* arr, int len)
{for (int i = 0; i < len - 1; i++){// 假设当前位置i的元素是最小的,记录其索引为miniint mini = i;for (int j = i + 1; j < len; j++){// 如果发现更小的元素,则更新mini为当前更小元素的索引if (arr[j] < arr[mini]){mini = j;}}swap(&arr[mini], &arr[i]);}
}图示如下:
然后我们来讲一种略微高效一点的选择排序
优化:
- 其原理就是利用双指针,一个begin前指针,一个end后指针,记录下首尾两个位置
- 然后设置一个最小值,一个最大值,一开始最小值为begin,最大值为end,接着通过一个内层的for循环从begin到end去做一个遍历,若是找到比这个最小值还要小的,就更新最小值;若是找到比这个最大值还要大的,就更新最大值
很简单又直观,我们来看一下代码
注意:同时交换可能会改变原先最大或者最小元素的位置。因此我们需要进行判断。
(若是这个max最大值与begin重合了,那么此时在更新max只需要更新一下max值就可以了)
//交换两个数据
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void SelectSort(int* arr, int n)
{int begin = 0; // 未排序部分的起始索引int end = n - 1; // 未排序部分的结束索引while (begin < end){int maxi = begin;int mini = begin;// 遍历未排序部分,找到最小值和最大值for (int i = begin + 1; i <= end; i++){if (arr[i] < arr[mini]){mini = i; // 更新最小值的位置}if (arr[i] > arr[maxi]){maxi = i; // 更新最大值的位置}}// 将当前范围的最小值交换到未排序部分的开始位置Swap(&arr[begin], &arr[mini]);// 如果begin与maxi重合,则更新maxiif (maxi == begin){maxi = mini;}// 将当前范围的最大值交换到未排序部分的结束位置Swap(&arr[end], &arr[maxi]);// 缩小未排序部分的范围++begin;--end;}
}2.3选择排序时间复杂度分析
-
从上面这两种选择排序的方式来看,它们都属于O(N2),而且选择排序无论是在随机排序还是顺序排序下,其时间复杂度都是O(N2),所有说这种排序的效率并不是很高,反倒是我们昨天介绍的直接插入排序来得好,因为若数组是呈有序序列排列的,那直接插入排序的时间复杂度是可以达到O(N)的
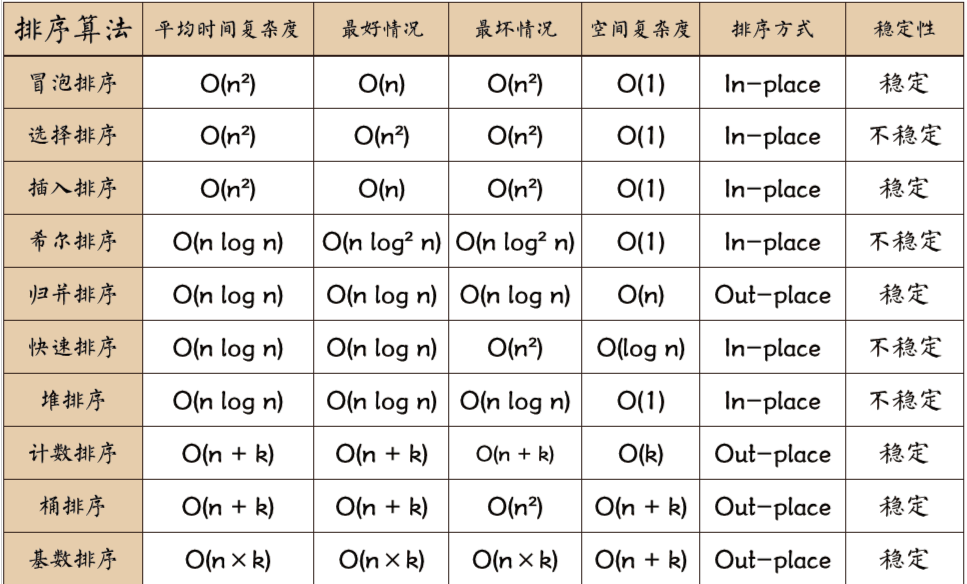
所以我们在选择排序算法的时候如果会使用其他的排序算法尽量就不要使用选择排序,看这张表就知道了。这里也只是给大家简单地介绍一下。
结束语:
本篇文章我们继续学习了两种排序算法——冒泡排序和选择排序。
感谢您的三连支持!!!

