数值计算2
接上节课——数值计算1-导论

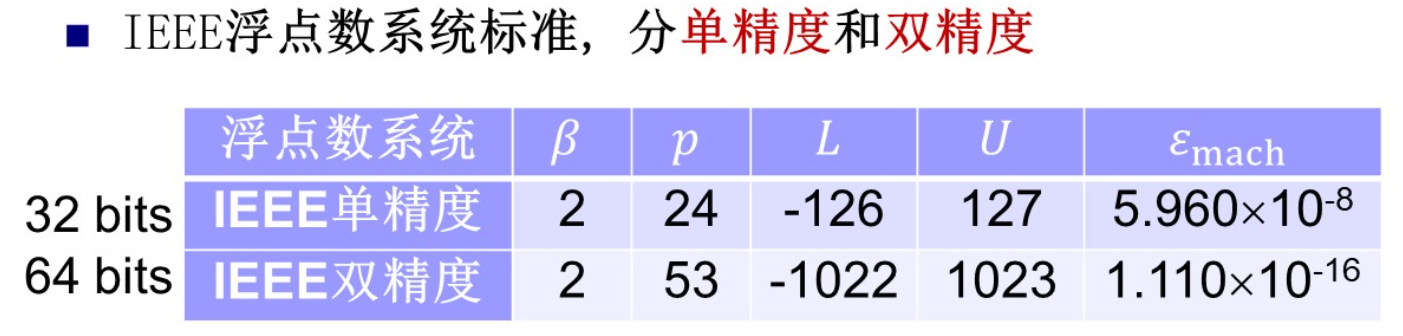
5.计算机浮点数系统
实数在计算机中的表示:2进制浮点数fl(x)
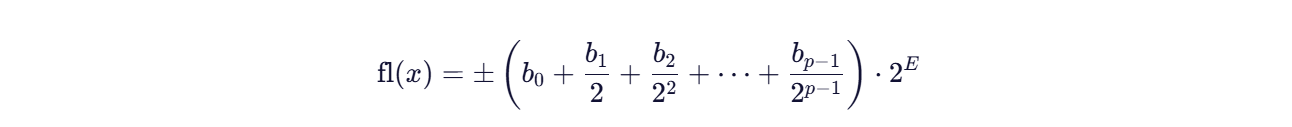

基数 β 在这里等于 2,表示这是一个二进制系统。这意味着所有的计算和表示都是基于 2 的幂次进行的。
指数 E:上限值 U,下限值 L
规范化(normalized):d0=1
规范化是指将浮点数表示成一种标准形式,使得尾数的第一个非零位总是 1。对于二进制浮点数,这意味着 d0=1。由于 d0 总是 1,因此在存储时可以省略它,从而节省空间。这种规范化的表示方式确保了数的表示唯一,并且所有尾数都是有效数字。
数的表示唯一、尾数都是有效数字、d0 不用存储(用该位表示 ± 的信息)
- 表示唯一:通过规范化,每个可表示的浮点数都有唯一的二进制表示。
- 有效数字:尾数中的每一位都代表了一个有效的数字,没有冗余。
- 省略 d0d0:由于 d0d0 总是 1,不需要存储它。通常,这个位置用来存储符号位,表示数的正负
浮点数有限个,非均匀的分布在数轴上
机器精度:对于一个具有 p 位尾数的二进制浮点数系统,机器精度 ε 可以定义为
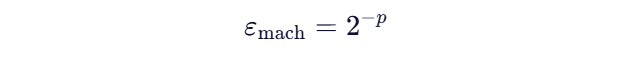

舍入
-
能在浮点数系统中准确表示的实数称为机器数。
-
如果实数 x 不是机器数,则在计算机中须用某个邻近的浮点数 fl(x) 近似它,近似的过程称为舍入
-
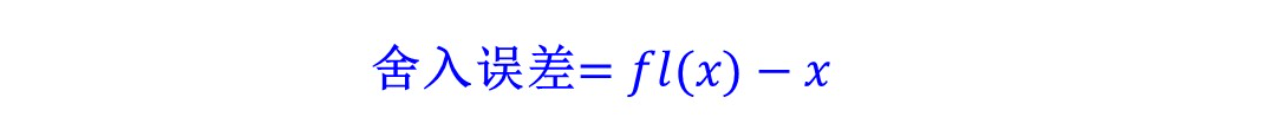
-
最近舍入:fl(x) 是与 x 最接近的浮点数,IEEE 默认。
如果 x 左、右两侧最近的浮点数与 x 的距离都相同,则一般取最后一位数字为偶数的那个。
例如,x=1.101 在 p=3 的二进制浮点数系统中,1.11 与 1.10 与 x 的距离相同,根据最近舍入规则,fl(x)=1.10
机器精度


6.数值计算中的规则
1.选用数值稳定性好的算法

2.避免大数吃小数


浮点加和浮点乘满足交换律,但不满足结合率
IEEE 754 标准明确规定:浮点加法和乘法必须满足交换律

3.避免抵消现象


4.调整计算顺序,避免中间计算结果出现上下溢出


5.简化计算步骤,减少运算次数


若初始数据误差较小,对于良态问题采用稳定算法,一定能得出比较准确的结果
判断
算法稳定,能保证在病态问题上得到好的近似值吗?
答:
算法稳定性(stability)并不自动意味着在病态问题上就能得到好的近似值。
病态问题的本质:病态(ill-conditioned)意味着:输入有极小的扰动,输出就会产生极大的变化。例如线性方程组 Ax=bAx = bAx=b,当 AAA 的条件数很大时,即使算法完全无误,数值解也会对 bbb 的微小噪声极度敏感。所以在病态问题上,不是“算法”先出错,而是问题本身不稳定。
算法稳定性的含义
-
稳定算法的直观意思是:它的计算误差不会额外放大,结果就像是在略微扰动了输入后得到的精确解。
-
换句话说,稳定算法保证误差主要来自问题本身,而不是算法的实现。
-
例如,解线性系统时,高斯消元的带主元选取版本是稳定的,而不选主元的可能是不稳定的。
稳定性与病态问题的关系
-
如果问题本身是良态的(well-conditioned),稳定算法能得到高精度解。
-
但如果问题本身是病态的,即使算法稳定,结果依然可能差,因为真实解本身对输入噪声非常敏感。
-
所以:稳定性 ≠ 精度保证;稳定性只是确保你不会因为数值方法“雪上加霜”
7.迭代算法的收敛速度

算法的收敛速度


p阶准确度

8.算法的计算性能

