当前位置：首页 > news >正文

LeetCode算法日记 - Day 41: 数据流的中位数、图像渲染

news 2025/9/15 8:35:41

1. 数据流的中位数

1.1 题目解析

1.2 解法

1.3 代码实现

2. 图像渲染

2.1 题目解析

2.2 解法

2.3 代码实现

1. 数据流的中位数

https://leetcode.cn/problems/find-median-from-data-stream/

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

实现 MedianFinder 类:

MedianFinder() 初始化 MedianFinder 对象。
void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

示例 1：

输入
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1);    // arr = [1]
medianFinder.addNum(2);    // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3);    // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0

提示:

-105 <= num <= 105
在调用 findMedian 之前，数据结构中至少有一个元素
最多 5 * 104 次调用 addNum 和 findMedian

1.1 题目解析

题目本质：
维护“一个不断增长的整数序列的中位数查询”。本质是“动态插入 + 快速取中位数”。

常规解法：

直接用数组/列表存数，每次 addNum 后排序，findMedian 取中间/中间两数的平均。

问题分析：

排序或插入保持有序都会导致高复杂度：
- 每次插入后排序：O(n log n)；
- 有序插入：O(n)；
- 共 5*10^4 次操作会超时。
我们需要把“中位数”的结构性利用起来。

思路转折：

中位数把序列劈成“两半”：左半 ≤ 右半。
维护两个堆：
- 左堆（最大堆）装较小的一半，堆顶x 是左半最大；
- 右堆（最小堆）装较大的一半，堆顶 y 是右半最小；
保持不变式：
- 尺寸：size(left) == size(right) 或 size(left) == size(right) + 1；
- 有序：max(left) ≤ min(right)。
这样：
- 奇数个：中位数是 left.peek()；
- 偶数个：中位数是 (left.peek() + right.peek()) / 2（注意小数与溢出）。

1.2 解法

算法思想：

新数先依据与 left.peek() 的比较决定归属：≤ 放左，否则放右。
插入后若尺寸失衡：
- 左比右多 2：把左堆堆顶挪到右堆；
- 右比左多 1：把右堆堆顶挪回左堆。
始终维持 max(left) ≤ min(right) 与尺寸不变式。

i）维护两个优先队列：left 为最大堆（较小一半），right 为最小堆（较大一半）。

ii）addNum(num)：

若 left 为空或 num ≤ left.peek()，放入 left，否则放入 right。
尺寸再平衡：
- 若 left.size() == right.size() + 2，right.offer(left.poll())；
- 若 right.size() == left.size() + 1，left.offer(right.poll())。

iii）findMedian()：

若总数为奇数，返回 left.peek()；
若为偶数，返回 ((long)left.peek() + (long)right.peek()) / 2.0（防止整除与溢出）。

易错点：

比较器溢出：b - a 可能溢出，建议用 Integer.compare(b, a)。
偶数取平均：必须用 / 2.0 做浮点除法，并在相加前转 long 以防溢出。
尺寸不变式：最终保证 left.size() == right.size() 或 left.size() == right.size() + 1。
有序不变式：插错堆或忘记再平衡会破坏 max(left) ≤ min(right)。

1.3 代码实现

import java.util.PriorityQueue;class MedianFinder {// left: 最大堆，装较小的一半；right: 最小堆，装较大的一半private PriorityQueue<Integer> left;private PriorityQueue<Integer> right;public MedianFinder() {left  = new PriorityQueue<>((a, b) -> Integer.compare(b, a)); // max-heapright = new PriorityQueue<>();                                 // min-heap}public void addNum(int num) {// 1) 先按与 left.peek() 的关系放入对应堆if (left.isEmpty() || num <= left.peek()) {left.offer(num);} else {right.offer(num);}// 2) 尺寸再平衡：left 只能比 right 多 1if (left.size() == right.size() + 2) {right.offer(left.poll());} else if (right.size() == left.size() + 1) {left.offer(right.poll());}}public double findMedian() {int total = left.size() + right.size();if ((total & 1) == 1) {           // 奇数：left 多一个return left.peek();} else {                          // 偶数：两堆顶求平均return ((long) left.peek() + (long) right.peek()) / 2.0;}}
}

复杂度分析：

时间：每次 addNum 为 O(log n)（堆操作），findMedian 为 O(1)。
空间：O(n)（存储所有元素于两堆）。

2. 图像渲染

https://leetcode.cn/problems/flood-fill/description/

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。你也被给予三个整数 sr , sc 和 color 。你应该从像素 image[sr][sc] 开始对图像进行上色填充。

为了完成 上色工作：

从初始像素开始，将其颜色改为 color。
对初始坐标的 上下左右四个方向上 相邻且与初始像素的原始颜色同色的像素点执行相同操作。
通过检查与初始像素的原始颜色相同的相邻像素并修改其颜色来继续重复此过程。
当没有其它原始颜色的相邻像素时停止操作。

最后返回经过上色渲染修改后的图像。

示例 1:

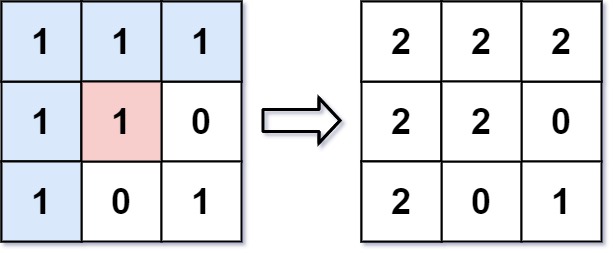
输入：image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, color = 2

输出：[[2,2,2],[2,2,0],[2,0,1]]

解释：在图像的正中间，坐标 (sr,sc)=(1,1) （即红色像素）,在路径上所有符合条件的像素点的颜色都被更改成相同的新颜色（即蓝色像素）。

注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。

示例 2:

输入：image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0

输出：[[0,0,0],[0,0,0]]

解释：初始像素已经用 0 着色，这与目标颜色相同。因此，不会对图像进行任何更改。

提示:

m == image.length
n == image[i].length
1 <= m, n <= 50
0 <= image[i][j], color < 216
0 <= sr < m
0 <= sc < n

2.1 题目解析

题目本质：
这是一个经典的「区域扩展」问题：从起点 (sr, sc) 出发，把所有与起点颜色相同且四向连通的像素染成新颜色。换句话说，就是在二维网格上做「连通块标记」。

常规解法：
最直观的办法是递归 DFS：从起点出发，遇到相同颜色就递归下去。直到走到边界或者颜色不同为止。

问题分析：

递归 DFS 在网格最大 50×50 时还可以用，但如果网格更大，就可能栈溢出。
我们要考虑更稳妥的解法：使用队列实现 BFS，避免深递归。
复杂度上：每个点最多访问一次，因此理论上是 O(m×n)，可以接受。

思路转折：
为了避免重复访问，需要有“访问过的标记”。在本题里，不需要额外 visited 数组，因为一旦我们把某点颜色改为 color，它就不会再等于原始颜色 tmp，自然不会重复入队。这是典型的「状态压缩」。

2.2 解法

算法思想：

用队列 BFS，从起点出发。
每次出队一个像素 (a,b)，染色为新颜色。
扫描它的四个邻居 (x,y)，若在边界内且颜色等于 tmp，则入队并等待染色。
直到队列为空，返回修改后的图像。

i）读取起点颜色 tmp，若 tmp == color，说明已经染色好，直接返回。

ii）初始化队列 q，起点 (sr, sc) 入队。

iii）循环直到队列为空：

取出队头 (a,b)，将 image[a][b] = color。
遍历四个方向：
- 新坐标 (x,y) = (a+dx[i], b+dy[i])
- 检查边界合法性 0<=x<m && 0<=y<n
- 检查颜色是否等于原色 image[x][y] == tmp
- 满足条件则入队。

iiii）返回最终图像。

易错点：

边界条件要检查 (x,y)，不是 (a,b)。
if (tmp == color) 必须提前返回，否则会死循环。
“访问标记”要靠染色本身，不能忘记更新 image[a][b]。

2.3 代码实现

class Solution {// 四个方向：右、左、下、上int[] dx = {0, 0, 1, -1};int[] dy = {1, -1, 0, 0};public int[][] floodFill(int[][] image, int sr, int sc, int color) {int tmp = image[sr][sc];if (tmp == color) return image; // 避免死循环int m = image.length, n = image[0].length;Queue<int[]> q = new LinkedList<>();q.offer(new int[]{sr, sc});while (!q.isEmpty()) {int[] num = q.poll();int a = num[0], b = num[1];image[a][b] = color; // 染色，相当于 visitedfor (int i = 0; i < 4; i++) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && image[x][y] == tmp) {q.offer(new int[]{x, y});}}}return image;}
}

复杂度分析：