算法——递推求解

1. 递推求解



• 问题描述：5人年龄问题中，第n个人比第n-1个人大2岁，已知第1个人10岁，求第5个人年龄
• 数学公式：f(n)=10+(n-1)*2（时间复杂度O(1)）
• 递推公式：
  • 边界条件：f(1)=10
  • 状态转移方程：f(n)=f(n-1)+2（时间复杂度O(1)）
• 教学目的：为动态规划做铺垫，理解状态转移方程的概念

2. 菲波那契数列的起源

• 历史背景：公元1225年意大利比萨数学竞赛题
• 兔子问题描述：
  • 1 月：有 1 对小兔；
  • 2 月：这对小兔长成 1 对大兔 ；
  • 3 月：这对大兔生下 1 对小兔，此时有 1 大兔 + 1 小兔 ；
  • 4 月：原来的大兔继续存活且又生下 1 对小兔，3 月出生的小兔长成大兔，此时有 2 大兔 + 1 小兔（共 3 对） ；
  • 5 月：4 月的 2 对大兔各生下 1 对小兔，4 月的 1 对小兔长成大兔 ，此时有 3 大兔 + 2 小兔（共 5 对） 。

3. 菲波那契数列的递推关系

• 递推关系：
  • 边界条件：f(1)=1,f(2)=1
  • 状态转移方程：f(n)=f(n-1)+f(n-2)（n>2）
• 生物学解释：
  • f(n-1)：上月存活的兔子总数
  • f(n-2)：上月可生育的大兔数量（即前月的总数）
• 数学特性：
  • 相邻项比值趋近黄金分割：
  • 前几项序列：1,1,2,3,5,8,13,21,34...
• 扩展思考：递推关系不仅限于前一项，可能与多项相关（如本例涉及前两项）

4、应用案例

1. 例题：直线分割平面

• 
• 问题描述：在一个平面上有一个圆和n条直线，这些直线中每一条在圆内同其他直线相交，假设没有3条直线相交于一点，求这些直线将圆分成多少区域。
• 小规模分析：
  • n=1：f(1)=2（一条直线将圆分成2部分）
  • n=2：f(2)=4（两条相交直线将圆分成4部分）
  • n=3：f(3)=7（三条两两相交直线将圆分成7部分）
• 递推公式：
  • 增量法：第n条直线与前面n−1条直线相交，产生n−1个交点，将第n条直线分成n段，每段增加一个区域。
  • 状态转移方程：f(n)=f(n−1)+n
• 方法总结：
  • 分析思路：从已知小规模问题出发，通过增量变化推导大规模问题解。
  • 关键点：新增直线与已有直线的交点数量决定了区域增量。

2. 例题：折线分割平面

• 问题描述：平面上有n条折线，这些折线最多能将平面分割成多少块？（这里的折现类似 “∠”，但两条边是无限延伸的射线）
• 与直线问题的区别：
  • 交点数量：两条折线最多有4个交点（vs 直线只有1个交点）
  • 增量计算：第n条折线与前n−1条折线最多产生4(n−1)个交点
• 递推公式：
  • 段数计算 ：4(n−1)个交点将第n条折线分成4(n−1)+1段
  • 状态转移方程：f(n)=f(n−1)+4(n−1)+1
• 方法验证：
  • n=1：f(1)=2
  • n=2：f(2)=7（与图示验证一致）
• 核心思想：虽然问题形式变化，但分析方法和直线分割问题本质相同。
• 图解：

3. 例题：骨牌铺方格

• 
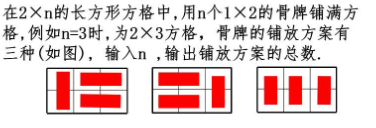
• 问题描述：在2×n的长方形方格中，用n个1×2的骨牌铺满方格，求铺放方案总数。
• 基本情况：
  • 当 n=1 时：方格是 2×1 的，骨牌只能竖放（因为骨牌是 1×2，竖放刚好占满 2×1），所以只有 1 种铺法，即 f(1)=1。
  • 当 n=2 时：方格是 2×2 的，有两种铺法：
    • 两个骨牌都竖放；
    • 两个骨牌都横放（上下各一个横放的骨牌，刚好占满 2×2）。
    • 所以 f(2)=2。
  • 当 n=3 时：方格是 2×3 的，有 3 种铺法（就像题干里的图那样），所以 f(3)=3。

现在思考：如果已经知道 n−1 和 n−2 时的铺法数，怎么求 n 时的铺法数？

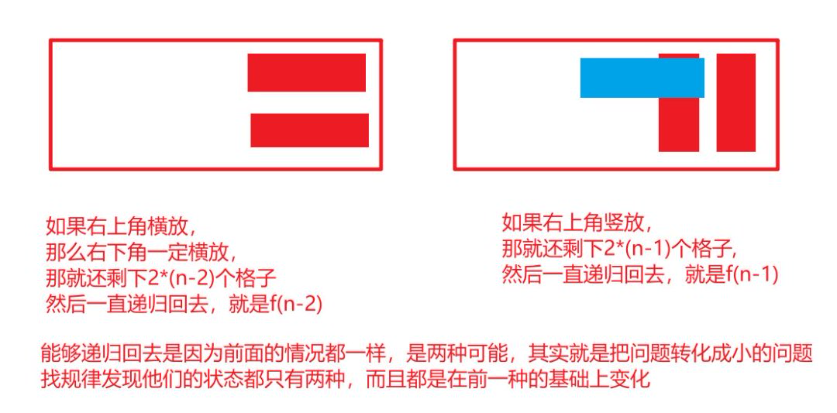
我们聚焦右上角的骨牌，它只有两种放法：

• 情况 1：右上角骨牌竖放

此时，右上角的竖放骨牌占了 2×1 的位置，剩下的区域是 2×(n−1) 的方格（因为总长度是 n，去掉竖放的 1 列，剩下 n−1 列）。

而铺 2×(n−1) 方格的方法数，就是 f(n−1)（因为问题结构和 “铺 2×n 方格” 是一样的，只是规模小了 1）。

• 情况 2：右上角骨牌横放

横放的话，右上角的骨牌占了 “上半部分的 1×2”，那为了铺满，它正下方的骨牌也必须横放（否则下方的 1×1 区域没法用 1×2 的骨牌铺满）。

这时候，这两个横放的骨牌一共占了 2×2 的位置，剩下的区域是 2×(n−2) 的方格（总长度 n，去掉横放的 2 列，剩下 n−2 列）。

铺 2×(n−2) 方格的方法数，就是 f(n−2)。

总铺法数：因为 “竖放” 和 “横放” 是两种互斥的情况（右上角骨牌要么竖放，要么横放，没有其他可能），所以总铺法数是这两种情况的和，即：f(n)=f(n−1)+f(n−2)

• 图解：

• 方法启示：
  • 问题分解：将大问题分解为结构相同的小问题
  • 边界条件：明确最小规模问题的解是递推基础
• 扩展思考：
  • 该递推关系与斐波那契数列相同
  • 体现了动态规划中"最优子结构"的思想：要解决 “铺 2×n 方格” 的问题，可以分解成 “铺 2×(n−1) 方格” 和 “铺 2×(n−2) 方格” 这两个更小的、结构相同的子问题。只要解决了子问题，就能通过组合子问题的解得到原问题的解。

4. 例题：多种骨牌铺方格

• 
• 问题描述：用1×1、1×2、1×3三种骨牌铺满1×n的长方形，求铺法总数f(n)。例如n=3时有四种铺法：
  • 三个1×1骨牌

  • 1×1+1×2骨牌（两种排列方式）

  • 一个1×3骨牌
• 递推公式推导：
  • 分类依据：以最后一个格子的覆盖方式为分类标准
  • 三类情况：

    • 1×1覆盖：前n−1格任意铺，共f(n−1)种

    • 1×2覆盖：最后两格被覆盖，前n−2格任意铺，共f(n−2)种

    • 1×3覆盖：最后三格被覆盖，前n−3格任意铺，共f(n−3)种

  • 状态转移方程：f(n)=f(n−1)+f(n−2)+f(n−3)
  • 图例：
  • 
• 实现建议：
  • 避免递归实现（时间复杂度指数级爆炸）
  • 推荐使用数组存储的递推方式（时间复杂度O(n)）

为什么这么说呢？我们来具体分析一下

以之前的骨牌铺放问题（递推式 f(n)=f(n−1)+f(n−2)+f(n−3)）为例，用递归计算 f(5) 时：

f(5) 依赖 f(4)、f(3)、f(2)；

f(4) 又依赖 f(3)、f(2)、f(1)；

f(3) 依赖 f(2)、f(1)、f(0)……

可以发现，很多子问题会被重复计算（比如 f(3) 会被 f(4) 和 f(5) 都调用一次，f(2) 会被更多次调用）。

这种 “重复计算” 会导致时间复杂度呈指数级增长（比如斐波那契数列的递归时间复杂度是 O(2n)，骨牌问题类似）。当 n 很大时（比如 n=50），递归会消耗极多时间，甚至 “卡死” 程序。

那为什么推荐使用数组存储的递推方式？

递推是 “自底向上” 的思路：先计算小的 n（如 f(0)、f(1)、f(2)），再逐步推导大的 n（如 f(3)、f(4)……f(n)）。

用数组存储递推的核心是：

定义一个数组 dp，其中 dp[i] 表示 “铺 1×i 长方形的方法数”。

先初始化基础情况：dp[0] = 1，dp[1] = 1，dp[2] = 2（对应骨牌问题的小例子）。

然后从 i=3 开始，根据递推式 dp[i] = dp[i-1] + dp[i-2] + dp[i-3] 计算每个 dp[i]。

这样做的好处是：

没有重复计算：每个 dp[i] 只计算一次，直接用前面已经算好的 dp[i-1]、dp[i-2]、dp[i-3]。

时间复杂度 O(n)：只需要遍历 1 到 n 一次，时间复杂度是线性的，即使 n 很大（比如 n=105），也能快速计算。

就是相当于，递归每次都要计算，但是数组可以把计算好的数据存储起来，下次就可以直接用，就不需要再次计算了

那是不是所有递归问题都可以用数组？

大部分有 “重叠子问题” 和 “最优子结构”的递归问题（比如动态规划类问题，像斐波那契数列、骨牌铺放、爬楼梯等），都可以用 “递推 + 数组存储” 来优化。但也有例外：

无重叠子问题的递归：比如 “二叉树的前序遍历”，每个子树的遍历是独立的，没有重复计算，可以直接用递归来访问根节点左节点，右节点，这时候递归和递推（手动模拟栈）的效率差异不大，甚至递归更简洁。

需要深度优先搜索的问题：比如 “迷宫寻路”，递归的深度优先搜索（DFS）思路更直接，若用递推模拟可能复杂且没必要（因为子问题不重叠）。

按照计算这么多，数组会不会太占内存？

通常不会，原因有两个：

• 空间复杂度可控：

以骨牌问题为例，数组的大小是 O(n)（n 是问题规模）。如果 n 是 “合理范围”（比如 n≤106），数组存储的空间是可接受的（一个长度为 106 的 int 数组，占约 4MB 内存，对现代计算机来说微不足道）。

• 可以优化空间（滚动数组）：

很多递推问题中，计算 f(n) 只依赖前几个状态（比如斐波那契数列 f(n) 只依赖 f(n−1)、f(n−2)）。这时候不需要存整个数组，只需存最近的几个状态，即 “滚动数组”。

比如斐波那契数列，用三个变量 a, b, c 分别存 f(n−2)、f(n−1)、f(n)，空间复杂度直接降到 O(1)。

可能会有个疑惑，为什么只会用到最近几个？用三个变量 a, b, c 分别存 f(n−2)、f(n−1)、f(n)，往前一个递归，不是需要用到前一个数据，再往前又要用到，那不是需要存储前面所有的结果吗？

斐波那契数列的递推式是 f(n)=f(n−1)+f(n−2)（n≥2，且 f(0)=0,f(1)=1）。

观察递推过程：

计算 f(2) 时，只需要 f(1) 和 f(0)；

计算 f(3) 时，只需要 f(2) 和 f(1)；

计算 f(4) 时，只需要 f(3) 和 f(2)；

……

计算 f(n) 时，只需要前两个状态 f(n−1) 和 f(n−2)，更早的状态（如 f(n−3)、f(0)）不再需要。

因此，不需要存储所有历史结果，只需保存 “最近的两个状态” 即可：

用变量 a 存 f(n−2)，b 存 f(n−1)；

计算 f(n)=a+b 后，更新 a = b，b = f(n)，为下一次计算做准备。

这样，空间复杂度从 O(n)（用数组存所有 f(0) 到 f(n)）优化到 O(1)（只存 3 个变量），且不影响结果的正确性

就相当于想要计算最后的结果，只需要递归得到结果存到数组里，然后下一个得到结果直接覆盖，最后一步的结果只需要最后覆盖得到的计算就好，不需要历史结果

但是这样每次都需要重复计算，不能复用，如果还要计算不同的，就又要重新递归存储覆盖，不是很不方便吗？

这个问题主要是要看场景

• 场景 1：只需要 “最终结果”

比如 “求 f(100)”，用滚动优化可以一次性从 f(0) 推到 f(100)，过程中覆盖存储，最终得到 f(100)。此时不需要 “复用中间结果”，滚动优化很高效。

• 场景 2：需要 “多个中间结果”

比如 “同时求 f(10)、f(20)、f(30)”：

如果用滚动优化 “一次性推到 f(30)”，那么 f(10)、f(20) 的中间结果会被覆盖，无法直接复用。

这种情况下，若需要多次查询不同 n 的结果，更适合用 “数组存储所有结果”（初始化时计算并保存 f(0) 到 f(30)，之后查询直接取数组元素）。

5. 递推求解基本方法

1）初始状态确认

• 核心原则：必须能直接求解初始小规模问题的解
• 确定方法：
  • 根据递推公式的"深度"确定需要多少初始值
  • 例如：f(n)=f(n−1)+f(n−2)+f(n−3)需要先求出f(1),f(2),f(3)
• 示例验证：

  • f(1)=1（仅1×1一种铺法）

  • f(2)=2（两个1×1或一个1×2）

  • f(3)=4（如题干所示四种情况）

2）问题分解假设

• 基本思想：假设所有规模小于N的子问题都已解决
• 数学表述：已知f(1),f(2),...,f(N−1)的值
• 应用要点：该假设是递推可行性的理论基础

3）状态转移分析

• 关键步骤：
  • 枚举规模为N时的所有可能情况
  • 将每种情况表示为已解决的子问题组合
  • 通过子问题解的组合得到当前问题的解
• 实现技巧：
  • 选择适当的分类标准（如例题中以"最后格子覆盖方式"分类）
  • 确保分类既不重复也不遗漏

4）实现方式对比

• 递归实现：
  • 缺点：存在大量重复计算，时间复杂度指数级增长
  • 改进：记忆化搜索（需额外存储空间）
• 递推实现：
  • 优势：自底向上计算，时间复杂度O(n)
  • 实现方式：使用数组顺序存储中间结果
• 选择建议：
  • 优先采用递推实现
  • 当问题结构复杂时考虑记忆化搜索

6. 例题：排队问题

1）问题描述

• 题目要求：校长希望所有学生排成一队，要求女生不能单独站立。即队列中可以没有女生，若有女生则其边上必须有其他女生。
• 示例说明：

  • n=1：只能是一个男生（M），共1种合法队列

  • n=2：两种合法队列（MM或FF），MF和FM不合法

  • n=3：四种合法队列（MMM、MFF、FFM、FFF）

  • n=4：通过枚举可得7种合法队列

2）递推分析

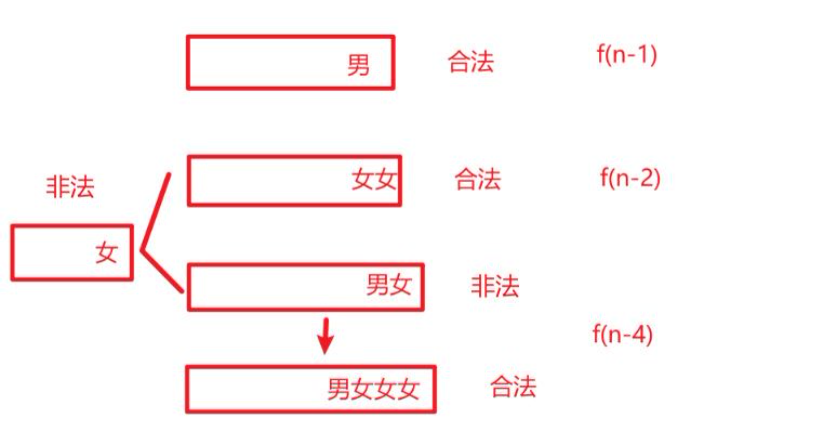
• 情况 1：最后一个人是男生（M）

因为男生没有 “不能单独站” 的限制，所以只要 “前 n−1 个人组成的队列合法”，再在最后加一个男生，整个队列依然合法。

因此，这种情况的数量为 f(n−1)。

• 情况 2：最后一个人是女生（F）

女生不能单独站，所以最后两个人必须都是女生（否则最后一个女生会 “单独”）。此时需要进一步细分 “前 n−2 个人组成的队列是否合法”：

• 子情况 2.1：前 n−2 个人组成的队列合法

此时，前 n−2 人合法，最后再加上 “FF”（两个女生），整个队列依然合法。

这种情况的数量为 f(n−2)。

• 子情况 2.2：前 n−2 个人组成的队列非法

前 n−2 人非法，但最后要凑出 “FF”，说明前 n−2 人的最后两位是 “MF”（这样加上 “FF” 后，整体最后两位是 “MF”→“FF”？不，更准确的逻辑是：前 n−2 人非法，但 “前 n−4 人合法”，且第 n−3、n−2 位是 “MF”，这样加上 “FF” 后，最后四位是 “MFFF”，能保证最后两位是 “FF”，且整体合法）。

简单来说：前 n−4 人合法，然后固定接 “MF”，最后再接 “FF”，这样总长度为 n，且最后两位是 “FF”。

这种情况的数量为 f(n−4)。

• 图解：

• 二维状态法
  • 状态定义：
    • f1(n)：以男生结尾的合法队列数
    • f2(n)：以女生结尾的合法队列数
  • 状态转移：
    • f1(n) = f1(n-1) + f2(n-1)（前n-1合法即可）
    • f2(n) = f2(n-1) + f1(n-2)（必须保证最后两个女生）
  • 总解：f(n) = f1(n) + f2(n)
  • 具体分析：

m(n)：长度为 n，最后一个是男生（M）的合法队列数；

f(n)：长度为 n，最后一个是女生（F）的合法队列数；

总合法数 total(n)=m(n)+f(n)

1. 推导 m(n)

最后一个是男生（M），因为男生无 “单独” 限制，所以前 n−1 个位置组成的队列只要合法，最后加一个男生就合法。

因此：m(n)=total(n−1)

2. 推导 f(n)

最后一个是女生（F），根据限制 “女生不能单独”，所以最后两个必须都是女生（否则最后一个女生会 “单独”）。此时需要保证 “前 n−2 个位置的队列合法，且最后两位是女生”。

进一步分析 “前 n−2 个位置的队列是否合法”：

若前 n−2 个位置合法：直接在后面加 “FF”，合法，数量为 total(n−2)。

若前 n−2 个位置非法：但要凑出 “最后两位是 FF”，需满足 “前 n−4 个位置合法，且第 n−3、n−2 位是 “MF”（这样加 “FF” 后，最后四位是 “MFFF”，合法）”，数量为 total(n−4)。

因此：

f(n)=total(n−2)+total(n−4)

3. 总递推式

总合法数 total(n)=m(n)+f(n)，代入 m(n) 和 f(n) 的表达式：

total(n)=total(n−1)+total(n−2)+total(n−4)

3）解题技巧

• 分类依据：优先选择直观的分类标准（如性别），再考虑合法性等抽象属性
• 边界处理：特别注意n≤4时的特殊情况需要单独处理
• 验证方法：通过小规模枚举（如n=1,2,3,4）验证递推公式的正确性
• 历史背景：该题目源自2005年浙大宁波理工学院的校赛题目，是经典的递推问题案例

7. 例题：字符串合法性判断

• 问题描述：长度为n的字符串由A/B/C组成，限制条件：
  • A不能接在B后面
  • B不能接在C后面
  • C不限制
• 具体分析：

我们定义 3 个状态（对应最后一个字符是 A/B/C）：

endA​(n)：长度为 n，最后一个字符是 A 的合法字符串数；

endB​(n)：长度为 n，最后一个字符是 B 的合法字符串数；

endC​(n)：长度为 n，最后一个字符是 C 的合法字符串数；

总合法数 f(n)=endA​(n)+endB​(n)+endC​(n)。

1. 推导 endA​(n)

最后一个字符是 A，根据限制 “A 不能接在 B 后面”→ 前一个字符不能是 B，可以是 A 或 C。

因此，前 n−1 个字符的最后一位是 A 或 C，所以：

endA​(n)=endA​(n−1)+endC​(n−1)

2. 推导 endB​(n)

最后一个字符是 B，根据限制 “B 不能接在 C 后面”→ 前一个字符不能是 C，可以是 A 或 B。

因此，前 n−1 个字符的最后一位是 A 或 B，所以：

endB​(n)=endA​(n−1)+endB​(n−1)

3. 推导 endC​(n)

最后一个字符是 C，无限制→ 前一个字符可以是 A、B 或 C。

因此，前 n−1 个字符的最后一位是 A、B 或 C，所以：

endC​(n)=endA​(n−1)+endB​(n−1)+endC​(n−1)

4. 总递推式

总合法数 f(n)=endA​(n)+endB​(n)+endC​(n)

• 方法优势：通过二维状态分解使问题简化，避免直接推导复杂公式

8. 例题：连线方案数



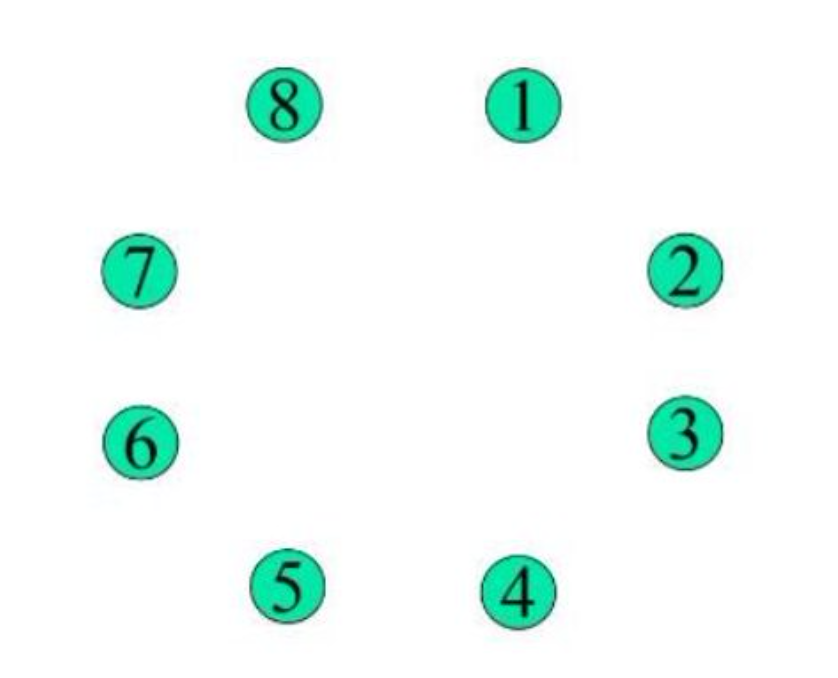
• 问题描述：2n个点围成圆圈，用n条不相交直线两两连接，求方案数
• 初始条件：

  • f(1)=1（2个点）

  • f(2)=2（4个点）

• 关键观察：
  • 连接限制：固定点1只能与偶数点连接（避免交叉）
  • 分类依据：根据点1的连接对象划分情况
• 具体分析：

设 f(n) 表示 “2n 个点围成圆，用 n 条不相交弦连接的方案数”。

分类讨论：固定一个点的连接对象

为了避免弦交叉，固定 “点 1” 的连接目标（所有点对称，选点 1 不影响结果）。

根据几何性质，点 1 只能连接偶数点（若连奇数点，必然与其他弦交叉）。假设点 1 连接 “点 2k”（k 从 1 到 n），此时圆被分成左右两个独立区域：

左侧区域：包含 2(k−1) 个点（点 2 到点 2k−1），需要用 k−1 条弦连接，方案数为 f(k−1)；

右侧区域：包含 2(n−k) 个点（点 2k+1 到点 2n），需要用 n−k 条弦连接，方案数为 f(n−k)。

递推关系：子问题的组合

对于每一个 “点 1 连点 2k” 的情况，总方案数是 “左侧方案数 × 右侧方案数”（因为左右区域独立，方案可自由组合）。

由于 k 可以取 1 到 n（对应点 1 连点 2,4,…,2n），所以总方案数 f(n) 是所有 k 对应的 “左右方案数乘积” 之和：

为了和常见形式统一，令 i=k−1（则 k=i+1），当 k 从 1 到 n 时，i 从 0 到 n−1，因此递推式可改写为：

9. 卡特兰数

（1） 递推公式（最常用形式）

卡特兰数的递推关系为：

初始条件：

这个递推式的含义是：第 n 个卡特兰数，等于所有 “前 i 个卡特兰数” 与 “后 n−1−i 个卡特兰数” 的乘积之和（和圆上点连接的递推式完全一致）。

（2）通项公式

卡特兰数的通项公式可以通过组合数推导得出：

        

其中是组合数，表示从 2n 个元素中选 n 个的组合数。

（3）案例

我们再来回顾一下刚刚那道题：圆上 2n 点连接问题

问题：2n 个点围成圆，用 n 条不相交的弦两两连接，求方案数。

分析过程：

分治逻辑：固定一个点（如点 1），它只能连偶数点（避免交叉）。假设点 1 连点 2k，则圆被分成左右两个独立区域，左侧有 2(k−1) 个点（方案数 Ck−1​），右侧有 2(n−k) 个点（方案数 Cn−k）。

递推关系：总方案数是所有 k 对应的 “左侧方案数 × 右侧方案数” 之和，即，与卡特兰数递推式一致。

初始条件：n=1 时（2 个点），方案数 C1​=1；n=2 时（4 个点），方案数 C2​=2，符合卡特兰数初始条件。

因此，该问题的解就是第 n 个卡特兰数。

（4）其他经典卡特兰数问题

1. 括号匹配问题

问题：有 n 对括号（( 和 )），求所有合法的括号排列数（如 n=2 时，合法排列为 (())、()()，共 2 种）。

分析：

选第一个左括号 (，它必须和某个右括号 ) 匹配。假设第 k 个位置是与之匹配的右括号，则左边有 k−1 对括号（方案数 Ck−1​），右边有 n−k 对括号（方案数 Cn−k​）。

递推关系：，与卡特兰数一致。

2. 出栈序列问题

问题：一个栈（先进后出），有 n 个元素依次入栈，求所有可能的出栈序列数（如 n=2 时，序列为 [1,2]、[2,1]，共 2 种）。

分析：

假设第一个出栈的元素是第 k 个入栈的元素，则它之前有 k−1 个元素已经出栈（方案数 Ck−1​），之后有 n−k 个元素出栈（方案数 Cn−k​）。

递推关系：，与卡特兰数一致。

3. 二叉树计数问题

问题：有 n 个节点，求能构成的不同形态的二叉树数目。

分析：

选一个节点作为根节点，左子树有 i 个节点（方案数 Ci​），右子树有 n−1−i 个节点（方案数 Cn−1−i​）。

递推关系：​，与卡特兰数一致。