机器学习-方差和偏差
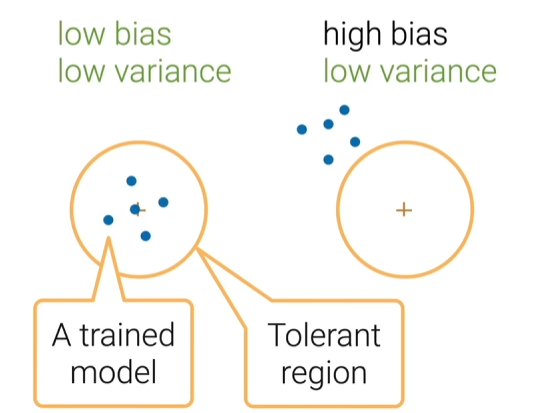
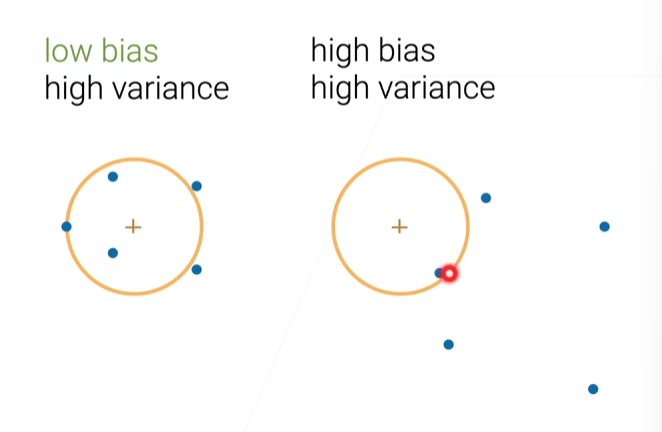
偏差-方法分解
- 从y=f(x)+εy=f(x)+\varepsilony=f(x)+ε中采样数据D={(x1,y1),...,(xn,yn)}D=\{(x_1,y_1),...,(x_n,y_n)\}D={(x1,y1),...,(xn,yn)}
- 通过从D中最小化MSE学习fˆ\^{f}fˆ,我们希望对于不同的D,生成的fˆ\^{f}fˆ都是好的
ED[(y−fˆ(x))2]=E[((f−E[fˆ])+ε−(fˆ−E[fˆ]))2]=(f−E[fˆ])2+E[ε2]+E[(fˆ−E[fˆ])2]=Bias[fˆ]2+Var[fˆ]+σ2\begin{equation} \begin{split} E_D[(y-\^{f}(x))^2]&=E[\left((f-E[\^{f}])+\varepsilon-(\^{f}-E[\^{f}])\right)^2]\\&=(f-E[\^{f}])^2+E[\varepsilon^2]+E[(\^{f}-E[\^{f}])^2]\\&=Bias[\^{f}]^2+Var[\^{f}]+\sigma^2 \end{split} \end{equation}ED[(y−fˆ(x))2]=E[((f−E[fˆ])+ε−(fˆ−E[fˆ]))2]=(f−E[fˆ])2+E[ε2]+E[(fˆ−E[fˆ])2]=Bias[fˆ]2+Var[fˆ]+σ2
其中E[f]=f,E[ε]=0,Var[ε]=σ2E[f]=f,E[\varepsilon]=0,Var[\varepsilon]=\sigma^2E[f]=f,E[ε]=0,Var[ε]=σ2,ε\varepsilonε独立于fˆ\^{f}fˆ
减少偏差和方差
减少偏差
- 用更复杂的模型(在神经网络中增加层和隐藏单元)
- Boosting
- Stacking
减少方差
- 用更简单的模型
- 正则化
- Bagging
- Stacking
降低σ2\sigma^2σ2
- 提升数据
集成学习
Boosting,Stacking,Bagging称为集成学习
即:通过多个模型提高预测性能
