当前位置：首页 > news >正文

【论文笔记】RadarOcc: Robust 3D Occupancy Prediction with 4D Imaging Radar

news 2025/9/13 5:59:41

原文链接：https://arxiv.org/abs/2405.14014

1. 任务定义

给定4D雷达张量（4DRT） $V∈RR×A×E×DV\in\mathbb R^{R\times A\times E\times D}$ ，目标是预测3D占用 $O={oi}i=1H×W×LO=\{o_i\}_{i=1}^{H\times W\times L}$ ，其中 $oi∈{c0,c1,⋯,cC}o_i\in\{c_0,c_1,\cdots,c_C\}$ 为空（ $c_0$ ）或某个类别 $c_i(i>0)$ 。4DRT的 $R, A, E, D$ 分别为距离、水平角、俯仰角和多普勒维度的区间数，且元素为测量的功率。

2. 概述

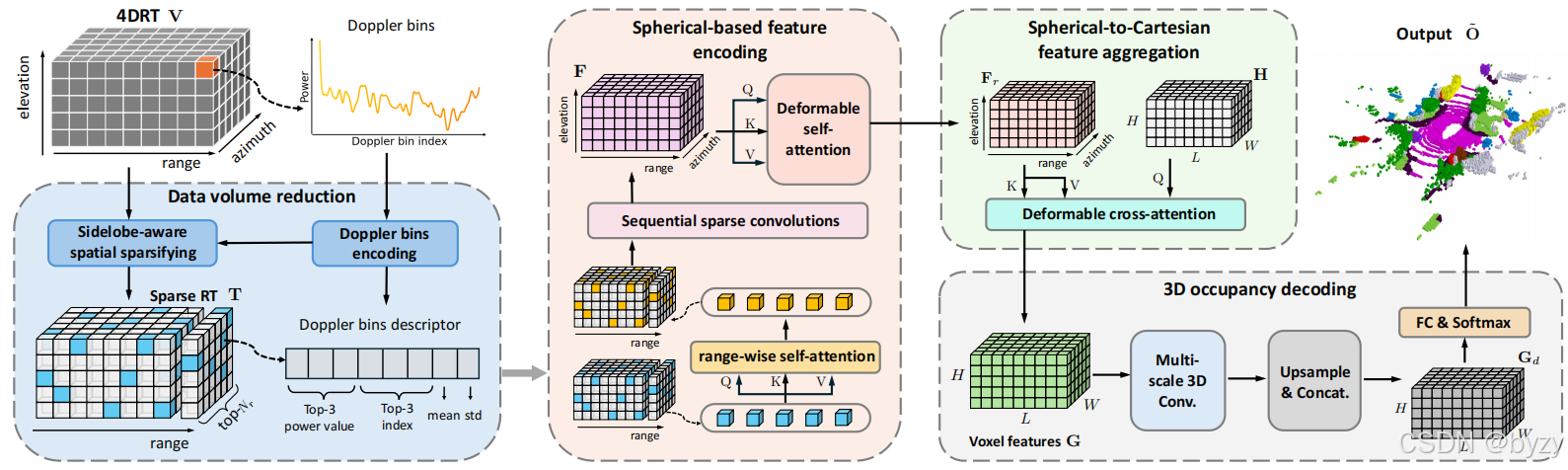
在这里插入图片描述
RadarOcc包含4个组件。在输入网络前，4DRT的体积会被压缩，以在不损失关键信息的条件下提高效率。为避免插值误差，本文直接在球坐标下编码空间特征，而不转化到笛卡尔坐标下；此后与笛卡尔坐标下定义的3D体查询交互。逐距离的自注意力用于减轻旁瓣，稀疏卷积和可变形注意力用于快速编码和聚合。

3. 数据体积压缩

原始的4DRT几乎不可能直接使用（平均每帧500MB）。本文通过多普勒频段描述符编码以及旁瓣感知的空间稀疏化操作来减少数据体积。

3.1 多普勒频段描述符

与之前的方法将多普勒维度进行池化操作不同，本文认为多普勒维度的峰值位置和功率分布分别反应了物体的速度和置信度。本文将多普勒区间编码为描述符，取前三峰值功率及其对应索引，再加上平均功率和标准差。这样，数据被压缩为原来的 $D /8$ ，同时保留了多普勒维度的关键信息。

3.2 旁瓣感知的空间稀疏化

过去的方法通过保留一定百分比的高功率元素来生成稀疏张量，进一步减小数据量。但如下右图所示，留下的大量元素均位于相同距离，表现为旁瓣的伪影。
在这里插入图片描述
本文选择每个距离下的前 $N_r$ 个元素（基于多普勒维度的平均功率），从而减轻旁瓣。稀疏张量表示为 $T={ti∈RNr×(8+2)}i=1RT=\{t_i\in\mathbb R^{N_r\times (8+2)}\}_{i=1}^{R}$ 。额外的两个维度存储水平角和俯仰角索引。

4. 基于球坐标的特征编码

过去的方法将稀疏张量由极坐标转化为笛卡尔坐标进行编码，但这样会引入插值误差并破坏其均匀密度分布。本文直接在距离-水平角-俯仰角维度进行3D稀疏卷积。

4.1 逐距离的自注意力

为进一步减轻旁瓣影响，本文使用逐距离的自注意力机制作为初始特征编码操作。对每个距离下的元素 $ti∈Tt_i\in T$ ，使用8维多普勒频段描述符作为特征，2维索引被用于位置编码。

4.2 序列稀疏卷积

使用一组3D稀疏卷积编码球坐标稀疏体素，最后转化为密集3D特征 $F∈RRS×AS×ES×CfF\in\mathbb R^{\frac RS\times\frac AS\times\frac ES\times C_f}$ 。

4.3 可变形自注意力

使用3D可变形注意力，通过空间交互进一步细化和增强特征 $F$ 。
$f_r^q=DeformAttn(f^q,p^q,F)$

其中 $f^q$ （ $F$ 的元素）为查询特征， $p^q$ 为其对应的参考点， $f_r^q$ 为更新后体素 $F_r$ 的元素。

5. 球坐标到笛卡尔坐标的特征聚合

首先建立基于网格的查询 $H={hq∈RCf}q=1H×W×LH=\{h^q\in\mathbb R^{C_f}\}_{q=1}^{H\times W\times L}$ （大小与占用网格相同，特征维度与 $F_r$ 相同），每个查询 $h^q$ 对应了笛卡尔坐标下的一个3D点 $p^q$ 。将 $p^q$ 转化到球坐标下，并映射为 $F_r$ 中的索引 $Φ(pq)\Phi(p^q)$ ，作为参考点。执行可变形交叉注意力，得到输出 $G={gq∈RCf}q=1H×W×LG=\{g^q\in\mathbb R^{C_f}\}_{q=1}^{H\times W\times L}$ ：
$gq=DeformAttn(hq,Φ(pq),Fr)g^q=DeformAttn(h^q,\Phi(p^q),F_r)$

6. 3D占用解码和监督

使用3D卷积逐步下采样 $G$ 得到 $N_s$ 个尺度的特征，并上采样到同一大小拼接，得到 $Gd∈RH×W×L×NsCfG_d\in\mathbb R^{H\times W\times L\times N_sC_f}$ 。最后，使用占用头得到占用概率 $O~∈[0,1]H×W×L×(C+1)\tilde O\in[0,1]^{H\times W\times L\times (C+1)}$ 。