连续hash函数
需求:需要一个既能保证数据映射到滑动窗口索引,又能维持顺序连续性的哈希函数。
如果直接哈希 (**value % windowSize**),则:
- 数据会跳跃式映射,导致 索引不连续(如 100、101 可能落入 5、8)。
- 顺序性被破坏,无法找到某个索引开始的连续已完成任务。
最终方案:单调映射函数
✅ 要求
- 映射结果单调递增(较大
value对应较大index)。 - 可支持整数或时间戳等有序数据。
- **索引范围固定在 **
**[0, windowSize - 1]**。
方案 1:线性缩放(Linear Scaling)
适用于数据范围固定,步长可以线性分割:
public int mapToIndexLinear(long value) {return (int) ((value - minValue) * (windowSize - 1) / (maxValue - minValue));
}
📌 适用场景:
- 时间戳(如
1700000000000L~1700001000000L) - 股票价格(如
10.0~100.0)
🔹 优点:顺序性 100% 保证,且索引连续。
🔹 缺点:适用于数据分布均匀的情况。
方案 2:对数缩放
适用于数据呈指数级增长(如时间戳、价格):
public int mapToIndexLog(long value) {double logMin = Math.log(minValue);double logMax = Math.log(maxValue);double logValue = Math.log(value);return (int) ((logValue - logMin) / (logMax - logMin) * (windowSize - 1));
}
📌 适用场景:
- 指数级增长的时间戳(如
UNIX时间戳从1,500,000,000到1,700,000,000) - 股票价格(如
0.1~10000.0,涨跌幅大)
🔹 优点:保证稀疏数据均匀分布,且顺序不变。
🔹 缺点:对于等间隔数据,映射不够均匀。
方案 3:自适应分段映射
适用于数据分布不均匀:
public int adaptiveMapToIndex(long value) {if (value < 1000) return (int) (value / 10); // 低值时更细粒度if (value < 10000) return 100 + (int) ((value - 1000) / 100);return 200 + (int) ((value - 10000) / 500);
}
📌 适用场景:
- 日志时间(短时间密集、长时间稀疏)
- 市场交易数据(某些价格段交易密集,某些价格段交易稀疏)
🔹 优点:高频值细粒度映射,低频值粗略映射。
🔹 缺点:需要手动调整区间规则。
综合选择
| 数据类型 | 适用方案 | 适用范围 |
|---|---|---|
| 时间戳 (均匀分布) | mapToIndexLinear(value) | 交易时间、日志时间 |
| 指数增长数值 | mapToIndexLog(value) | 股票价格、指数增长数据 |
| 不均匀数据 | adaptiveMapToIndex(value) | 交易密集区域、自适应数据 |
👉** 推荐**:
- 线性映射 (
mapToIndexLinear) 适用于大多数递增数据(如时间戳)。 - 对数映射 (
mapToIndexLog) 适用于指数增长数据。 - 自适应映射 (
adaptiveMapToIndex) 适用于分布不均匀的场景。
🚀 可以选择最适合业务数据特点的方式,保证索引顺序和连续性!
对数缩放 (Log Scaling)
对数缩放 (Log Scaling) 详解
1. 为什么使用对数缩放?
在某些应用场景下,数据的取值范围跨度非常大,例如:
- 时间戳(
1700000000000L~1700001000000L) - 股票价格(
0.1~10000.0) - 指数增长数据(访问量、收益率)
如果直接使用线性映射 (**mapToIndexLinear**),低值区域会被映射到很少的索引,而高值区域会占据大量索引,导致:
- 低值数据不够精细,丢失信息
- 高值数据过于密集,浪费索引
👉 解决方案:对数缩放 (Log Scaling)
通过对数函数 log(value) 进行变换,使得数据分布更加均匀。
2. 对数缩放公式
希望将 value ∈ [minValue, maxValue]单调映射 到窗口索引 [0, windowSize - 1],公式如下:

log(value):将value转换到对数坐标log(minValue), log(maxValue):对数区间- 归一化到
[0, windowSize - 1]
Java 实现
public int mapToIndexLog(long value) {double logMin = Math.log(minValue);double logMax = Math.log(maxValue);double logValue = Math.log(value);return (int) ((logValue - logMin) / (logMax - logMin) * (windowSize - 1));
}
3. 对数缩放示例
假设:
minValue = 1maxValue = 1000windowSize = 10
计算几个关键值的索引:
| 值 (value) | log(value) | 归一化后索引 |
|---|---|---|
| 1 | 0 | 0 |
| 10 | 1 | 3 |
| 100 | 2 | 6 |
| 1000 | 3 | 9 |
可以看到:
- 低值 (
1 ~ 10) 之间的索引变化小(分布更细) - 高值 (
100 ~ 1000) 之间的索引增长更快(防止稀疏)
4. 对数坐标图
画一个对数坐标图,横轴 value,纵轴 log(value)。
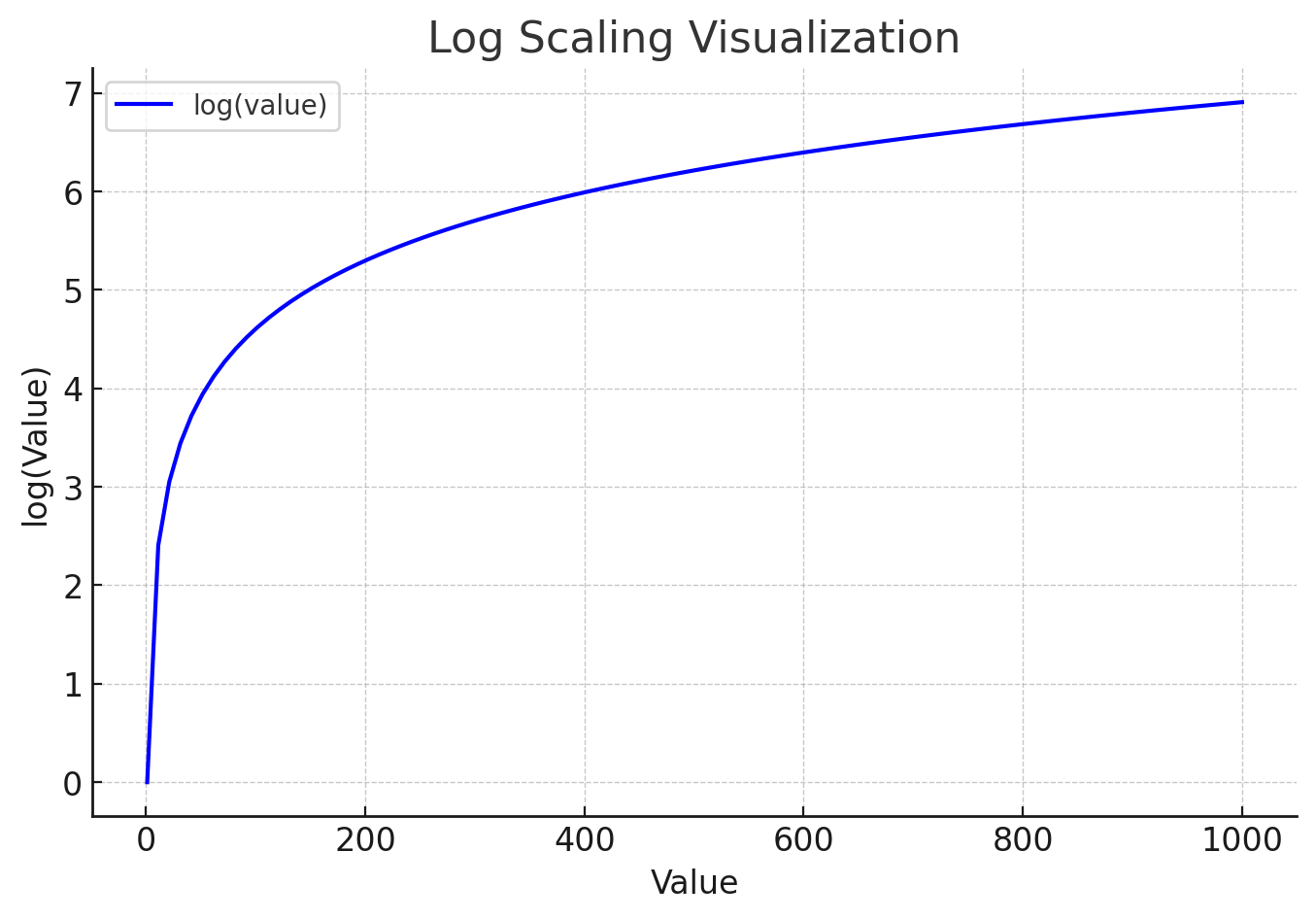
如图所示,对数函数 log(value)在小值区间增长快,在大值区间增长慢。这保证了:
- 低值部分索引变化较慢,映射更加精细。
- 高值部分索引变化快,避免占用太多索引。
如果数据跨度很大,对数缩放是一个非常合适的映射方式!
注

