当前位置：首页 > news >正文

对于单链表相关经典算法题：21. 合并两个有序链表及面试题 02.04. 分割链表的解析

news 2025/9/12 15:16:09

开篇介绍：

Hello 大家，在上一篇博客中，我们一同深入探讨了环形链表的约瑟夫问题，通过环形链表模拟与数学递推两种思路，拆解了 “环形计数淘汰” 的核心逻辑。无论是指针操作中对前驱节点的精准把控，还是递推公式里对问题规模的逐步缩减，相信都让大家对 “环形结构” 与 “逻辑转化” 有了更深刻的理解。而在今天的内容里，我们将把目光转向单链表的另外两个经典场景 ——有序链表的合并与链表的分割，聚焦于「21. 合并两个有序链表」和「面试题 02.04. 分割链表」这两道题目。

单链表作为数据结构中的 “基础建材”，其操作往往暗藏着对 “指针串联” 与 “逻辑重组” 的深层考验。合并两个有序链表，看似是简单的 “拼接”，实则需要在不破坏原有顺序的前提下，通过指针的灵活移动实现 “有序融合”；而分割链表则更像一场 “分类游戏”，需要按照特定规则（如数值大小）将链表拆分为两个部分，再重新串联成符合要求的新链表。这两道题虽场景不同，却有着共通的核心 ——如何通过指针的精准操控，实现链表节点的 “重新排列”。

为什么要深入研究这两类问题？因为它们背后藏着链表操作的底层逻辑：合并问题中 “比较 - 链接” 的循环，本质上是归并排序中 “合并阶段” 的简化版，掌握它能为后续复杂排序算法打下基础；而分割问题中 “双链表分别收集” 的思路，则与快速排序中的 “分区” 思想异曲同工，是理解 “按条件分类” 问题的关键。无论是实际开发中的数据整合需求，还是算法面试中的逻辑设计考验，这些基础操作都扮演着不可或缺的角色。

在接下来的内容里，我们将从题目分析入手，一步步拆解解题思路。

先附上这两道题的链接，我们依旧是老样子，大家在看解析之前自行练练手，帮助大家理解题目：

21. 合并两个有序链表 - 力扣（LeetCode）https://leetcode.cn/problems/merge-two-sorted-lists/description/面试题 02.04. 分割链表 - 力扣（LeetCode）https://leetcode.cn/problems/partition-list-lcci/solutions/1/mian-shi-ti-0204-fen-ge-lian-biao-shuang-46vz/

21. 合并两个有序链表

这道题本质上不难，我们先看题目：

题意分析：

要深度剖析 “合并两个有序链表” 这道题，我们从题目本质、边界场景、算法设计约束等维度逐一拆解，确保对题意的理解精准且全面：

一、题目本质：有序结构的 “融合”

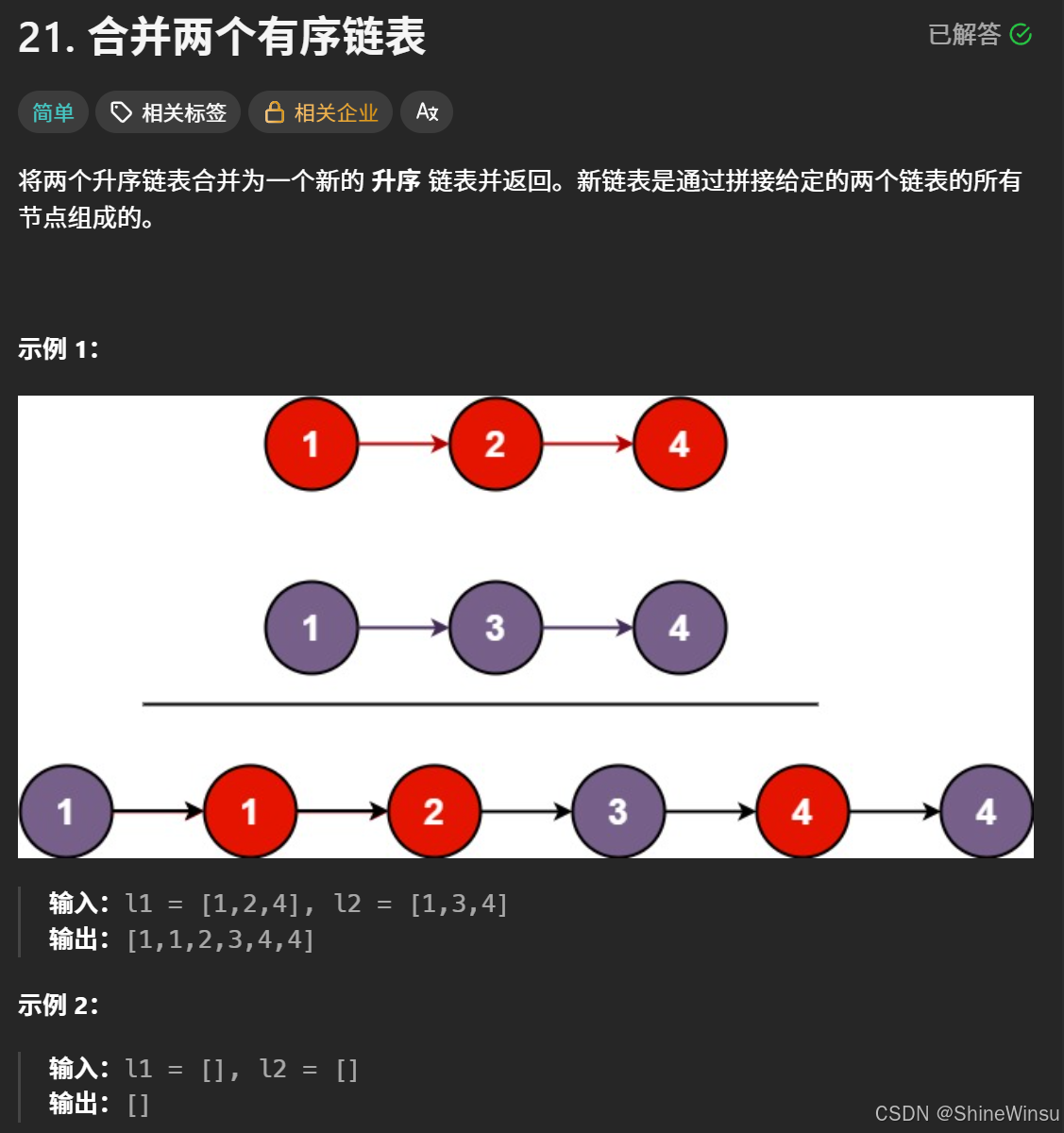
题目要求将两个非递减有序的链表（l1 和 l2），合并为一个非递减有序的新链表。这本质上是 **“有序序列的归并操作”**—— 利用两个输入链表已有的有序性，通过 “逐节点比较、按序拼接”，得到整体有序的结果。

类比生活场景：就像把两副已经按大小排好序的扑克牌，合并成一副更大的、仍按大小排序的牌堆，每次从两堆的 “顶部（当前节点）” 选较小的牌放入新堆。

二、输入输出的精准解读

1. 输入特性

链表结构：输入是两个单链表，每个节点包含 val（值）和 next（指向下一节点的指针）。
有序性约束：l1 和 l2 本身都是非递减的（即 “从小到大，允许相等”）。例如 l1 = [1,2,2,4]、l2 = [1,3,4] 是符合要求的输入。
节点数量范围：每个链表的节点数在 0 到 50 之间（包括空链表和最多 50 个节点的链表）。
节点值范围：节点的值是整数，且满足 -100 ≤ Node.val ≤ 100，这意味着值的大小跨度有限，无需考虑极端大数的特殊处理。

2. 输出要求

新链表的结构：新链表的节点由 l1 和 l2 的所有节点 “拼接” 而成（不能创建新节点，必须复用原有节点）。
有序性要求：新链表必须保持非递减顺序，即新链表中任意相邻节点 a、b，都满足 a.val ≤ b.val。

三、边界场景的全覆盖分析

题目通过 “示例 2” 和 “示例 3”，明确了需要处理的特殊输入场景，这些场景直接影响算法的鲁棒性：

1. 场景 1：两个链表均为空（示例 2）

输入：l1 = []，l2 = []
预期输出：[]
算法应对：需判断 “若两个链表都为空，直接返回空链表”。

2. 场景 2：其中一个链表为空（示例 3）

输入：l1 = []，l2 = [0]（或反之）
预期输出：[0]（直接返回非空的那个链表）
算法应对：需判断 “若 l1 为空，返回 l2；若 l2 为空，返回 l1”。

那么对于这道题，同样是有多种解法，不过在这里我只讲创建新链表的这一个做法，毕竟它并不复杂

进行解析：

对于本题，我们第一步肯定就是要先判断两个原链表是否为空，为空就直接返回NULL，这已经是基操了。

接着，我们便创建新链表newhead和newtail，这也是基本操作了。

然后，就到了本题的重头戏，首先，我们肯定要对两个原链表的数据一一进行比较，谁小，谁就进新链表中，然后进行插入的那一个链表进行节点后移，这边我们要格外注意，没有进行插入的（也就是在比较中较大的节点的那一个链表），它的节点是不能往后移的，要留在那里去和进行插入的那一个链表进行节点后移的节点再次比较大小。

那么，还有个问题，我们要怎么设置while循环的终止条件呢？其实也不难，首先我们知道，肯定是和那两个原链表有关的，只是具体是什么呢？经过上一段，我们已经知道了，还是需要两个原链表的不断移动的，所以，肯定是要两个链表的遍历不为空，但是，是设置哪一个呢？实际上，是两个都要不为空，因为我们还要预防空指针访问，比如说，有一个链表遍历完了，但是还有一个链表没有遍历完，那么这个时候还不退出while循环的话，很有可能进行空指针访问，因此，循环条件是while(l1!=NULL&&l2!=NULL)，至于大家可能会说，那么剩下的没有遍历完的那一个链表怎么办，那也简单，因为题目已经说了两个链表都是升序链表，而已经经过了循环，说明一个链表已经全部处理完了，也就是遍历完的那一个链表已经和为遍历完的那一个链表比较大小完了，所以当结束循环之后，我们直接把没有遍历完的那一个链表按照顺序全部尾插入新链表之中就行了

除此之外，希望大家不要忘记了当新链表为空时，我们要进行的操作，具体上面所述的具体代码如下：

typedef struct ListNode sl;struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{sl* l1=list1;sl* l2=list2;if(l1==NULL&&l2==NULL)//都为空链表{return NULL;}sl* newhead=NULL;sl* newtail=newhead;//创建新链表while(l1!=NULL&&l2!=NULL){if(newhead==NULL)//先对创建的新链表进行头插{if(l1->val>=l2->val){newhead=l2;newtail=newhead;l2=l2->next;//单独，防止出现相等的情况时，有一个被忽略到，当出现相等的情况是 }else if(l1->val<l2->val){newhead=l1;newtail=newhead;l1=l1->next;}}else{if(l1->val>=l2->val){newtail->next=l2;newtail=newtail->next;l2=l2->next;}else if(l1->val<l2->val){newtail->next=l1;newtail=newtail->next;l1=l1->next;}}}
}

再给上一版详细注释：

// 为链表节点结构体创建别名sl，简化后续代码书写
// 前提：struct ListNode的定义隐含包含两个成员：
//     - int val：存储节点的值
//     - struct ListNode* next：指向后续节点的指针
typedef struct ListNode sl;/*** 合并两个非递减有序链表为一个新的非递减有序链表* @param list1 第一个输入有序链表的头节点（可能为NULL）* @param list2 第二个输入有序链表的头节点（可能为NULL）* @return 合并后新链表的头节点（若两链表均为空则返回NULL）*/
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{// 1. 定义遍历指针，分别指向两个输入链表的当前待处理节点// l1：用于遍历list1，初始位置为list1的头节点sl* l1 = list1;// l2：用于遍历list2，初始位置为list2的头节点sl* l2 = list2;// 2. 处理边界情况：两个链表均为空时，直接返回NULL// 逻辑依据：没有任何节点可合并，结果必然为空if (l1 == NULL && l2 == NULL){return NULL;}// 3. 初始化新链表的控制指针// newhead：始终指向新链表的第一个节点（用于最终返回结果）// 初始为NULL表示新链表尚未创建任何节点sl* newhead = NULL;// newtail：始终指向新链表的最后一个节点（用于高效尾插操作）// 初始与newhead保持一致，确保链表为空时指针状态正确sl* newtail = newhead;// 4. 核心合并逻辑：同时遍历两个链表，按值大小顺序拼接节点// 循环条件：只有当两个链表都还有未处理的节点时才继续比较// 一旦其中一个链表遍历完毕（指针为NULL），则退出循环while (l1 != NULL && l2 != NULL){// 4.1 处理新链表的第一个节点（头节点创建）// 此时newhead为NULL，需要确定新链表的起点if (newhead == NULL){// 比较l1和l2当前节点的值，选择较小的节点作为头节点// 情况1：l1的值大于等于l2的值，选择l2节点作为头节点if (l1->val >= l2->val){newhead = l2;          // 新链表头指针指向l2当前节点newtail = newhead;     // 尾指针同步指向头节点（此时链表长度为1）l2 = l2->next;         // l2指针后移，指向原l2的下一个节点// 注意：此处包含l1->val == l2->val的情况，选择l2不影响有序性}// 情况2：l1的值小于l2的值，选择l1节点作为头节点else if (l1->val < l2->val){newhead = l1;          // 新链表头指针指向l1当前节点newtail = newhead;     // 尾指针同步指向头节点l1 = l1->next;         // l1指针后移，指向原l1的下一个节点}}// 4.2 新链表已有节点，进行常规尾插操作else{// 比较l1和l2当前节点的值，将较小的节点接入新链表尾部// 情况1：l1的值大于等于l2的值，接入l2当前节点if (l1->val >= l2->val){newtail->next = l2;    // 新链表尾部节点的next指向l2当前节点newtail = newtail->next; // 尾指针后移至新接入的节点（保持尾部特性）l2 = l2->next;         // l2指针后移，继续处理剩余节点}// 情况2：l1的值小于l2的值，接入l1当前节点else if (l1->val < l2->val){newtail->next = l1;    // 新链表尾部节点的next指向l1当前节点newtail = newtail->next; // 尾指针后移至新接入的节点l1 = l1->next;         // l1指针后移，继续处理剩余节点}}}// 5. 处理剩余节点：当其中一个链表已遍历完毕，将另一个链表的剩余部分接入新链表// 逻辑依据：输入链表本身是有序的，剩余节点无需比较可直接拼接

大家应该经过上述，便能初步理解了，下面我们再来解决一下对于未遍历完的链表对新链表的插入，其实不难，我们常规尾插就行了。

但是，还是有细节需要注意的，大家其实很可能只会这么写：

    //出来循环之后就代表有l1或者l2走到了末尾，也有可能是都走到了末尾//但是我们还是要进行判断，把未走到尽头的那一个链表的剩余的节点都加到新链表进去if(l1!=NULL){newtail->next=l1;newtail=newtail->next;l1=l1->next;}if(l2!=NULL){newtail->next=l2;newtail=newtail->next;l2=l2->next;//要记得移动节点哦}return newhead;
}

但是如果就这么提交了，就会报出空指针访问的错误，这是为什么呢？其实很简单，那就是我们忽略了两个链表中一个链表不为空链表，而另一个链表为空链表的问题，那么这个时候，是不会进入while(l1!=NULL&&l2!=NULL）循环的，而是会直接进入上述的代码，而在上述的代码中，我们又没有进行常规空链表判断，那么自然就会报错了，所以，真正的代码是这样：

// 处理l1链表剩余节点
if (l1 != NULL)
{// 若新链表为空（说明此前未处理任何节点）if (newhead == NULL){newhead = l1;       // 直接将l1作为新链表的头节点newtail = newhead;  // 尾节点同步指向头节点}else{newtail->next = l1; // 将l1剩余部分接入新链表尾部newtail = newtail->next; // 尾指针后移到新接入部分的末尾}l1 = l1->next; // l1指针后移，继续处理剩余节点（注：此处可省略，因剩余节点已整体接入）
}// 处理l2链表剩余节点
if (l2 != NULL)
{// 若新链表为空（应对示例3：一个链表为空，另一个非空的场景）if (newhead == NULL){newhead = l2;       // 直接将l2作为新链表的头节点newtail = newhead;  // 尾节点同步指向头节点}else{newtail->next = l2; // 将l2剩余部分接入新链表尾部newtail = newtail->next; // 尾指针后移到新接入部分的末尾}l2 = l2->next; // l2指针后移（注：同l1，此处可省略）
}

由此，本题结束，但是又没有完全结束，我们先看完整代码：

typedef struct ListNode sl;struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{sl* l1=list1;sl* l2=list2;if(l1==NULL&&l2==NULL)//都为空链表{return NULL;}sl* newhead=NULL;sl* newtail=newhead;//创建新链表while(l1!=NULL&&l2!=NULL){if(newhead==NULL)//先对创建的新链表进行头插{if(l1->val>=l2->val){newhead=l2;newtail=newhead;l2=l2->next;//单独，防止出现相等的情况时，有一个被忽略到，当出现相等的情况是 }else if(l1->val<l2->val){newhead=l1;newtail=newhead;l1=l1->next;}}else{if(l1->val>=l2->val){newtail->next=l2;newtail=newtail->next;l2=l2->next;}else if(l1->val<l2->val){newtail->next=l1;newtail=newtail->next;l1=l1->next;}}}//出来循环之后就代表有l1或者l2走到了末尾，也有可能是都走到了末尾//但是我们还是要进行判断，把未走到尽头的那一个链表的剩余的节点都加到新链表进去if(l1!=NULL){if(newhead==NULL){newhead=l1;newtail=newhead;}else{newtail->next=l1;newtail=newtail->next;}l1=l1->next;}if(l2!=NULL){if(newhead==NULL)//我们还要防止题目所给一个链表直接为空，另一个不为空的情况，如果为示例3，那么就会直接到这一步来，我们依然要使用头插新节点进新的空链表中去{newhead=l2;newtail=newhead;}else{newtail->next=l2;newtail=newtail->next;}l2=l2->next;//要记得移动节点哦}return newhead;
}

大家看着这么长一串代码，会不会有点无奈，太长了吧，而且我们还要不断的进行判断是否为空链表，好麻烦呀，每次都要重复。

诶，没事，针对这个情况，哨兵节点，它来了：

哨兵节点：

在链表操作中，哨兵节点（Sentinel Node） 是一个特殊的 “虚拟节点”，它不存储实际数据，仅用于简化链表的边界条件处理。它就像一个 “哨兵”，守卫在链表的头部（或尾部），让链表操作（如插入、删除、合并等）变得更统一、更简洁。

一、哨兵节点的核心作用

哨兵节点的设计初衷是消除 “空链表” 和 “非空链表” 的处理差异，避免在操作中频繁判断 “头节点是否为空”“指针是否越界” 等边界情况，从而简化代码逻辑。

举例：在合并两个有序链表时，如果没有哨兵节点，需要单独处理 “新链表第一个节点” 的创建（如判断newhead == NULL）；而有了哨兵节点，无论链表是否为空，都可以用统一的 “尾插” 逻辑处理所有节点。

二、哨兵节点的特点

不存储有效数据：哨兵节点的val值无实际意义（通常设为 0 或 - 1 等占位符）。

直接sl* smallhead=malloc(sizeof(sl));//哨兵节点就可以了，不用存储数据，它的next指针才是真正的新链表的头结点（有数据的第一个节点）

位置固定：通常位于链表的头部（称为 “头哨兵”），也可用于尾部（“尾哨兵”），但头哨兵更常用。
始终存在：无论链表是否为空，哨兵节点都存在，避免了 “链表为空时指针为 NULL” 的情况。

三、为什么需要哨兵节点？—— 解决边界痛点

没有哨兵节点时，链表操作往往需要处理大量边界条件，容易出错。例如：

向空链表插入第一个节点时，需要单独赋值给head；
从链表头部删除节点时，需要特殊处理head指针的更新；
合并两个链表时，需要判断新链表是否为空才能决定如何插入第一个节点。

而哨兵节点可以将这些 “特殊情况” 转化为 “普通情况”，让代码逻辑更统一。

四、实战对比：有无哨兵节点的代码差异

以 “合并两个有序链表” 为例，对比有无哨兵节点的实现：

1. 无哨兵节点（需处理边界条件）

struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {struct ListNode* newhead = NULL;struct ListNode* newtail = NULL;// 需单独处理第一个节点if (l1 != NULL && l2 != NULL) {if (l1->val <= l2->val) {newhead = l1;l1 = l1->next;} else {newhead = l2;l2 = l2->next;}newtail = newhead;} else if (l1 != NULL) {return l1; // 单独处理l2为空的情况} else {return l2; // 单独处理l1为空的情况}// 处理剩余节点while (l1 != NULL && l2 != NULL) {if (l1->val <= l2->val) {newtail->next = l1;l1 = l1->next;} else {newtail->next = l2;l2 = l2->next;}newtail = newtail->next;}// 需再次判断剩余链表if (l1 != NULL) newtail->next = l1;if (l2 != NULL) newtail->next = l2;return newhead;
}

2. 有哨兵节点（逻辑统一）

struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {// 创建哨兵节点（头哨兵）struct ListNode* sentinel = (struct ListNode*)malloc(sizeof(struct ListNode));sentinel->val = 0; // 无实际意义sentinel->next = NULL;// 尾指针指向哨兵节点，统一用尾插法处理所有节点struct ListNode* newtail = sentinel;// 无需单独处理第一个节点，直接循环比较while (l1 != NULL && l2 != NULL) {if (l1->val <= l2->val) {newtail->next = l1;l1 = l1->next;} else {newtail->next = l2;l2 = l2->next;}newtail = newtail->next;}// 剩余节点直接拼接，无需判断新链表是否为空newtail->next = (l1 != NULL) ? l1 : l2;// 哨兵节点的next即为新链表的头节点struct ListNode* result = sentinel->next;free(sentinel); // 释放哨兵节点（避免内存泄漏）return result;
}

五、哨兵节点的优势总结

简化代码逻辑：消除 “空链表” 与 “非空链表” 的处理差异，避免大量if-else判断。
减少边界错误：无需担心 “向空链表插入节点”“删除头节点” 等操作导致的指针异常。
统一操作流程：无论链表状态如何，都可以用相同的 “插入”“删除” 逻辑处理。

六、哨兵节点的适用场景

链表的合并（如mergeTwoLists）；
链表的插入 / 删除（尤其是头节点操作）；
链表的遍历与搜索（减少越界判断）；
复杂链表问题（如环形链表检测、相交链表查找等）。

七、注意事项

内存管理：哨兵节点是动态分配的，使用后需及时free，避免内存泄漏。
不滥用：简单链表操作（如单节点访问）无需哨兵节点，过度使用会增加内存开销。

通过哨兵节点，我们能将链表操作的复杂度从 “需要处理各种边界” 降低到 “统一逻辑流程”，这是数据结构中 “空间换简洁” 思想的典型应用。

所以，在知道了哨兵节点之后，本题的代码便能够大大减少了，而且不需要判断新链表是否为空了，完整代码如下：

//创建哨兵节点typedef struct ListNode sl;struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{sl* l1=list1;sl* l2=list2;if(l1==NULL&&l2==NULL)//都为空链表{return NULL;}sl* newhead=malloc(sizeof(sl));//创建了一个哨兵节点，这一个节点是没有存储数据的，但是它的next能够指向存有数据的头结点，有了这个之后，我们就可以避免要判断为空时进行头插sl* newtail=newhead;//创建新链表while(l1!=NULL&&l2!=NULL){if(l1->val>=l2->val){newtail->next=l2;newtail=newtail->next;l2=l2->next;}else if(l1->val<l2->val){newtail->next=l1;newtail=newtail->next;l1=l1->next;}}//出来循环之后就代表有l1或者l2走到了末尾，也有可能是都走到了末尾//但是我们还是要进行判断，把未走到尽头的那一个链表的剩余的节点都加到新链表进去if(l1!=NULL){newtail->next=l1;newtail=newtail->next;l1=l1->next;}if(l2!=NULL){newtail->next=l2;newtail=newtail->next;l2=l2->next;//要记得移动节点哦}return newhead->next;//返回哨兵节点的next指针，即新链表真正的头结点
}

到此，本题才算是大功告成，希望大家能够牢记哨兵节点这个知识点，它会在后面的双向链表中发挥大作用。

面试题 02.04. 分割链表

这道题的难度其实也就一般，关键在于我们思路的突破，我们先看题目：

题意分析：

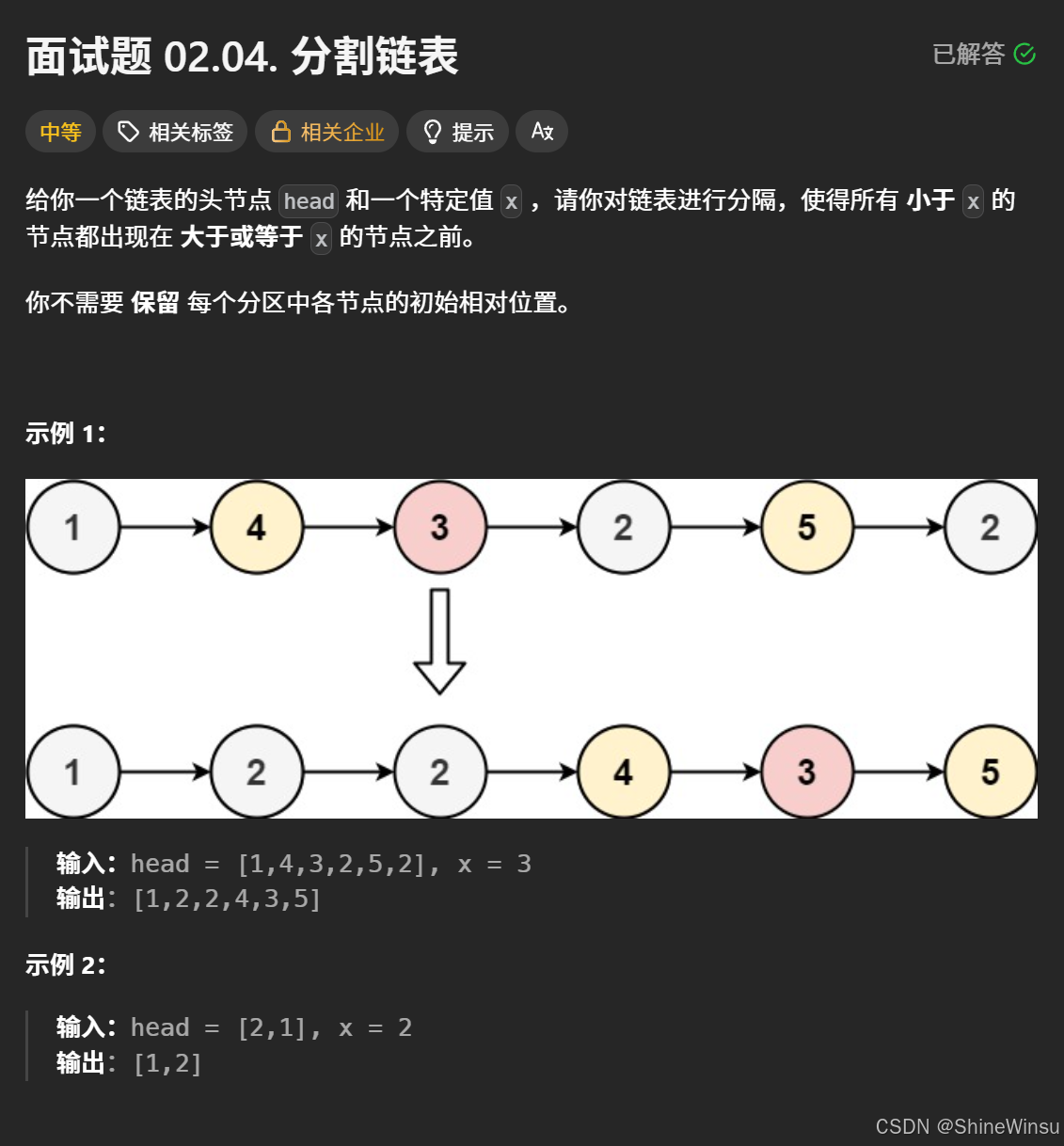
一、问题本质：按条件的 “链表分区”

题目要求将一个单链表分割为两部分：所有值小于 x 的节点在前，所有值大于或等于 x 的节点在后。这本质上是一种 “基于阈值的链表拆分与重组” 操作，核心是对节点进行 “分类归集”，不要求内部有序，但需严格保证前后分区的逻辑。

类比生活场景：就像将一堆数字卡片按 “小于 3” 和 “≥3” 分成两摞，再把第二摞接在第一摞后面，不关心每摞内部卡片的原始顺序。

二、输入输出的精准解读

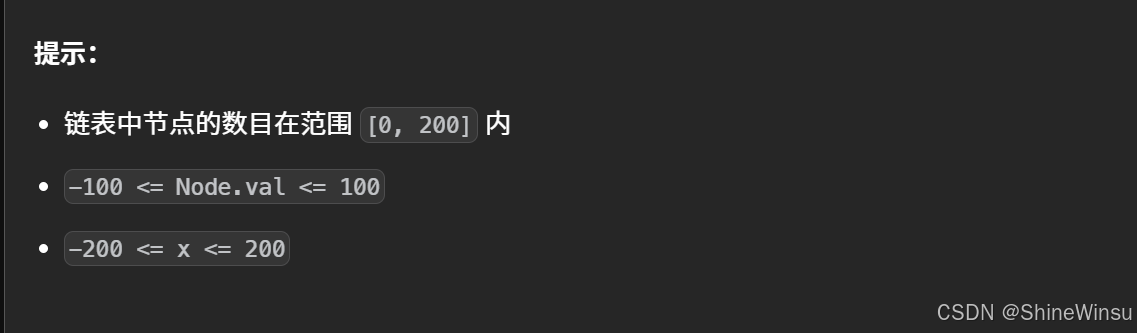
1. 输入特性

链表结构：输入是一个单链表（可能为空），每个节点包含 val（整数）和 next（指针）。
阈值 x：用于划分节点的临界值，类型为整数，范围 [-200, 200]。
节点范围：
- 节点数量：0 ≤ 节点数 ≤ 200（可能为空链表，或最多 200 个节点）。
- 节点值：-100 ≤ Node.val ≤ 100（值的跨度有限，无需特殊处理极值）。

2. 输出要求

分区逻辑：新链表必须满足 “前半部分所有节点值 < x，后半部分所有节点值 ≥ x”。
节点复用：必须使用原链表的节点（不能创建新节点），仅通过调整指针实现重组。
顺序无关性：无需保留每个分区内节点的原始相对顺序（这是与 “稳定排序” 的关键区别）。例如输入 [3,1,2] 且 x=3，输出 [1,2,3] 或 [2,1,3] 均正确。
无环约束：输出链表必须是合法单链表（尾节点 next 为 NULL，不能形成环）。

三、边界场景的全覆盖分析

题目隐藏了多种特殊情况，需在算法中妥善处理：

1. 场景 1：原链表为空

输入：head = NULL，x 任意。
预期输出：NULL（无节点可分割）。

剩下的大家可以自行思考一番为什么。

继续解析：

那么对于本题，依然是有很多种解法，不过在这里，我就只讲一种解法，那就是：双链表法。

因为根据我们对题目的分析，其实就是要把原链表中小于x的节点全部放在大于等于x的节点之前，那么我们的常规思路就是遍历法，但是很显然，有点麻烦了。

于是，我们的双链表法，也就应运而生了，同时，为了避免判断空链表的麻烦，我们这里依旧是使用哨兵节点进沙场秋点兵。

那么这个双链表是怎么个双链表法呢？其实也很好理解，那就是我们创建两个链表，一个是small链表，用来存储原链表中小于x的节点，另一个是big链表，用来存储原链表中大于x的节点。

实现如上步骤的代码，大家肯定是烂熟于心了，我们直接看代码：

//创建两个链表，一大一小typedef struct ListNode sl;struct ListNode* partition(struct ListNode* head, int x) 
{if(head==NULL){return NULL;}sl* bighead=malloc(sizeof(sl));//哨兵节点sl* bigtail=bighead;sl* smallhead=malloc(sizeof(sl));//哨兵节点sl* smalltail=smallhead;sl* temp=head;while(temp!=NULL){if(temp->val>=x){bigtail->next=temp;bigtail=bigtail->next;}else{smalltail->next=temp;smalltail=smalltail->next;}temp=temp->next;}

这个方法真正的难点在于循环后的代码，首先，为了实现题目要求，我们要把small链表的最后一个节点的next指针指向big链表的真正的头结点（也就是big链表的哨兵节点的下一个节点（bighead->next）），而且作为一个优秀程序员，我们要把我们所创建的哨兵节点释放掉，避免内存浪费，同时为了能顺利传回指针，我们还要设置变量去保存，然后再释放，具体如下：

smalltail->next=bighead->next;
sl* ret=smallhead->next;
free(smallhead);
free(bighead);
return ret;

但是如果我们就这么提交了，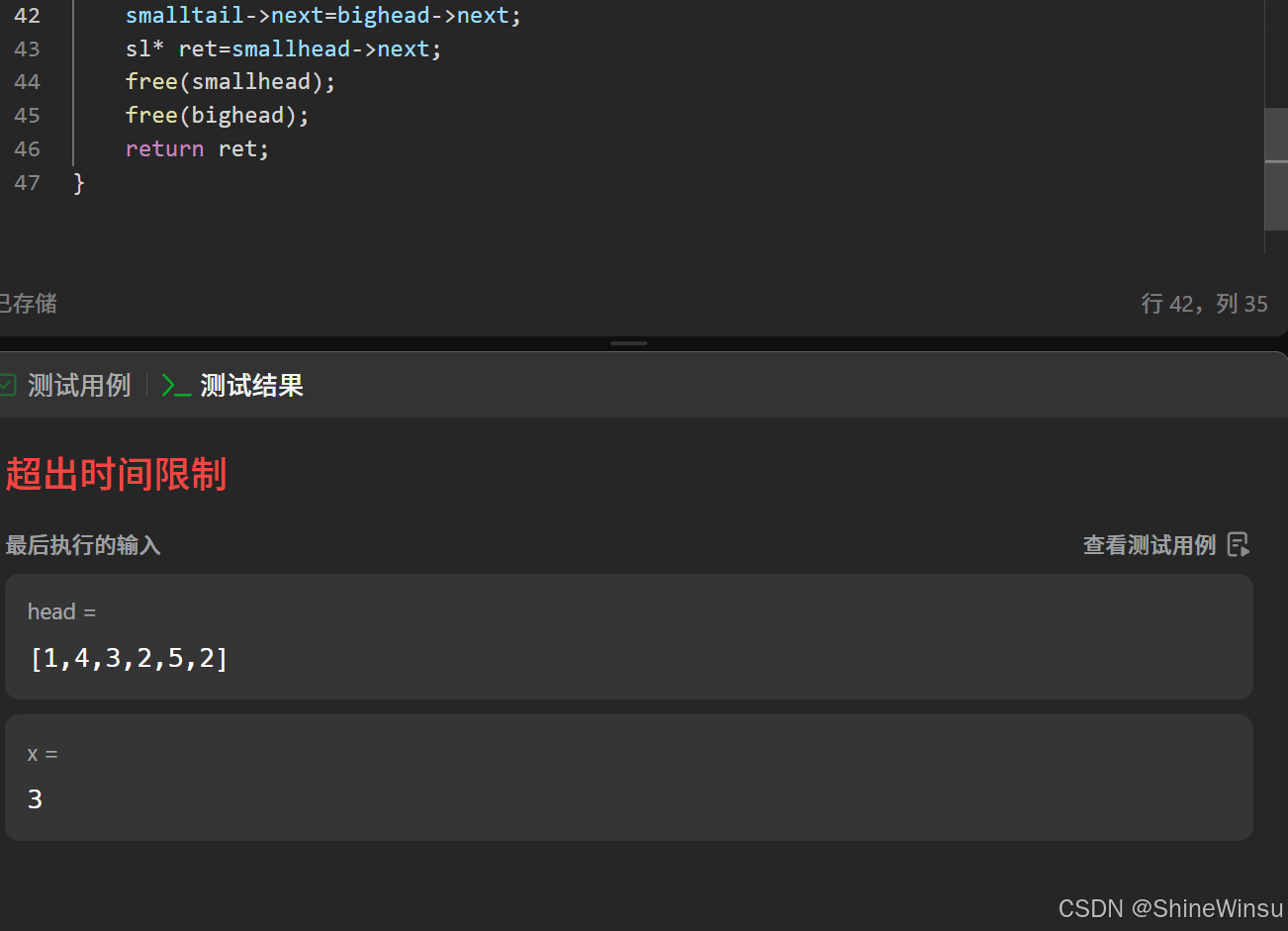

如图，就会如此报错，意思是代码运行陷入死循环了，那么这是为什么呢？其实问题就出现在bigtail身上，smalltail的next指针我们把它赋值为bighead->next,，但是我们可是没有对bigtail的next指针处理哦，大家可不要觉得它就是会为NULL，实则不然，就拿题目的示例来说，如果我们没有对bigtail的指针进行处理的话，由于我们是直接取用原链表的节点，所以此时bigtail的next指针还是指向原链表中节点5后面的节点2，这么一来，就会造成下图的情况：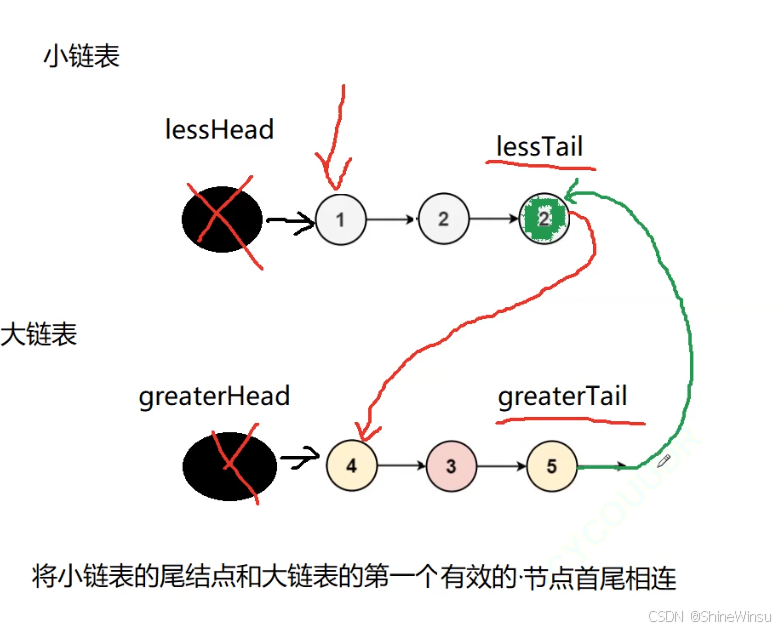

所以，我们要对bigtail->next赋值为NULL，这样子这个代码才算是完美无缺。下面就给出详细注释版本的完整代码：

// 为链表节点结构体创建别名sl，简化代码书写
// 结构体定义隐含为：
// struct ListNode {
//     int val;                // 节点存储的数值
//     struct ListNode* next;  // 指向后一个节点的指针
// };
typedef struct ListNode sl;/*** 分割链表核心函数* 功能：将所有值小于x的节点放在大于或等于x的节点之前* 参数：*   head - 原链表的头节点（可能为NULL，表示空链表）*   x    - 分割阈值，用于判断节点应该放在前半部分还是后半部分* 返回值：*   分割后新链表的头节点（若原链表为空则返回NULL）*/
struct ListNode* partition(struct ListNode* head, int x) 
{// 【边界处理1】如果原链表为空，直接返回NULL// 为什么要处理？因为空链表没有任何节点可分割，继续操作会导致无意义的指针访问if (head == NULL){return NULL;  // 空链表的分割结果还是空链表}// 【创建哨兵节点】使用两个哨兵节点分别管理两类节点// 哨兵节点作用：消除"空链表"和"非空链表"的处理差异，简化插入逻辑// 1. 创建用于存储"大于或等于x"节点的哨兵节点及尾指针sl* bighead = (sl*)malloc(sizeof(sl));  // 为大链表哨兵节点分配内存// 为什么用malloc？因为需要一个持久存在的虚拟节点，不能用栈上变量（函数结束会销毁）sl* bigtail = bighead;  // 大链表尾指针，初始指向哨兵节点（此时链表为空）bigtail->next = NULL;   // 哨兵节点的next初始化为NULL，确保链表终止符正确// 2. 创建用于存储"小于x"节点的哨兵节点及尾指针sl* smallhead = (sl*)malloc(sizeof(sl));  // 为小链表哨兵节点分配内存sl* smalltail = smallhead;  // 小链表尾指针，初始指向哨兵节点smalltail->next = NULL;     // 哨兵节点的next初始化为NULL// 【遍历原链表的指针】temp用于逐个访问原链表中的所有节点sl* temp = head;  // 从原链表的头节点开始遍历// 【核心循环：节点分类】遍历所有节点，按值分配到两个临时链表// 循环条件：temp != NULL → 当temp为NULL时，表示所有节点已处理完毕while (temp != NULL){// 情况1：当前节点的值大于或等于x → 放入大链表if (temp->val >= x){bigtail->next = temp;  // 将当前节点接入大链表的尾部// 为什么这样接入？尾指针的next指向新节点，实现"尾插"操作bigtail = bigtail->next;  // 尾指针后移到新接入的节点// 为什么移动？保证bigtail始终指向大链表的最后一个节点，便于下次尾插}// 情况2：当前节点的值小于x → 放入小链表else{smalltail->next = temp;  // 将当前节点接入小链表的尾部smalltail = smalltail->next;  // 小链表尾指针后移}// 移动遍历指针，处理下一个节点temp = temp->next;// 注意：这里无需修改原节点的next指针，因为后续会统一处理}// 【拼接两个链表】将大链表接在小链表的后面// smalltail是小链表的最后一个节点，其next应指向大链表的第一个有效节点// 为什么是bighead->next？因为bighead是哨兵节点，其next才是第一个有效节点smalltail->next = bighead->next;// 【关键操作：避免链表成环】// 大链表的最后一个节点（bigtail）的next必须手动设为NULL// 为什么？原链表中bigtail的next可能指向已被移到小链表的节点// 例如原链表：1→4→3（x=3），处理后bigtail指向4，原4的next是3（已移到小链表）// 若不设为NULL，新链表会出现4→3→...的环，导致遍历无法终止bigtail->next = NULL;// 【确定返回的头节点】新链表的头节点是小链表哨兵节点的next// 为什么？smallhead是哨兵节点，其next才是第一个有效节点（可能为NULL）sl* ret = smallhead->next;// 【释放哨兵节点内存】避免内存泄漏// 哨兵节点完成使命后必须释放，因为它们是用malloc分配的堆内存free(smallhead);free(bighead);// 【返回结果】返回分割后的新链表头节点return ret;
}

到此，本题大功告成。

结语：

到这里，关于「合并两个有序链表」和「分割链表」的解析就告一段落了。回顾这两道题，它们看似是单链表操作的基础练习，却藏着数据结构中最核心的思维方式 ——用指针串联逻辑，用抽象简化复杂。

合并链表时，我们从笨拙地处理空链表边界，到借助哨兵节点实现 “一键统一”，体会到了 “空间换简洁” 的智慧；分割链表时，通过双链表分类收集的思路，将 “按条件重组” 的难题拆解为 “遍历 - 归类 - 拼接” 的清晰步骤，更明白了 “分而治之” 的算法思想如何落地。这些看似细微的指针操作，实则是在训练我们对 “逻辑连贯性” 的把控 —— 每一次next指针的调整，都需要考虑前后节点的关联，稍有疏忽就可能导致链表断裂或成环。

其实，数据结构的魅力正在于此：它不像数学公式那样抽象，也不像业务逻辑那样繁琐，而是通过一个个具体的节点和指针，让我们直观地感受 “如何用代码构建秩序”。无论是合并时的 “有序融合”，还是分割时的 “分类重组”，本质上都是在训练我们 “拆解问题、设计流程、处理边界” 的能力 —— 而这些能力，恰恰是解决更复杂算法问题的基石。

或许你现在会觉得，反复琢磨这些基础题有些 “小题大做”。但请相信，当未来面对更复杂的链表问题（如 K 个一组翻转、环形链表 II），或是更抽象的数据结构（如树、图）时，今天在指针操作中培养的 “逻辑严谨性” 和 “抽象思维”，会成为你最有力的武器。

最后，希望你能带着这份对细节的执着和对逻辑的敏感，继续在算法的世界里探索。每一道题都是一次成长的契机，每一次调试都是与 bug 的正面交锋，而每一次 AC（Accepted）的背后，都是对 “如何让代码更优雅” 的深刻理解。

愿你在数据结构的海洋里，既能脚踏实地打磨基础，也能仰望星空探索未知。我们下一道题再见！