磁共振成像原理(理论)6:自由感应衰减 (Free Induction Decays)
回顾信号的产生和探测
复盘一下之前的内容,下面的总结如果看的不甚明白,建议再回顾之前的内容再往下看。
物体在外部磁场 B⃗0\vec B_{0}B0 处于热平衡态时,在空间位置 r\boldsymbol{r}r 的横向宏观磁化矢量的强度 ∣Mxy(r,0−)∣|M_{xy}(\mathbf{r},0-)|∣Mxy(r,0−)∣ 为0,仅剩 zzz 方向的纵向宏观磁化矢量的强度 ∣Mz(r,0−)∣|M_{z}(\mathbf{r},0-)|∣Mz(r,0−)∣ 。
一个 α\alphaα 脉冲激发后的t=0+t=0+t=0+ 时刻,在空间位置 r\boldsymbol{r}r 的 xyxyxy方向的横向分量∣Mxy(r,0+)∣|M_{xy}(\mathbf{r},0+)|∣Mxy(r,0+)∣为
∣Mxy(r,0+)∣=sinα⋅∣Mz(r,0−)∣=sinα⋅Mz0|M_{xy}(\mathbf{r},0+)| =sin \alpha \cdot |M_{z}(\mathbf{r},0-)| = sin \alpha \cdot M_z^0 ∣Mxy(r,0+)∣=sinα⋅∣Mz(r,0−)∣=sinα⋅Mz0
而后的任意 t(t>0)t\space(t>0)t (t>0) 时刻,在空间位置 r\boldsymbol{r}r 的xyxyxy方向的横向分量 Mxy(r,t)M_{xy}(\mathbf{r},t)Mxy(r,t) 为(实验室坐标系下的复数形式):
Mxy(r,t)=∣Mxy(r,0+)∣e−t/T2(r)e−i[ω(r)t+ϕe(r)]M_{xy}(\mathbf{r},t) = |M_{xy}(\mathbf{r},0+)|e^{-t/T_{2}(\mathbf{r})}e^{-i[\omega(\mathbf{r}) t+\phi_{e}(\mathbf{r})]} Mxy(r,t)=∣Mxy(r,0+)∣e−t/T2(r)e−i[ω(r)t+ϕe(r)]
其中e−t/T2(r)e^{-t/T_{2}(\mathbf{r})}e−t/T2(r)是空间位置 r\boldsymbol{r}r 的横向弛豫衰减;e−iω(r)t+ϕe(r)e^{-i\omega(\mathbf{r}) t+\phi_{e}(\mathbf{r})}e−iω(r)t+ϕe(r) 是自由进动,其进动频率 ω(r)\omega(\mathbf{r})ω(r) 也和位置有关,特别需要关注的是 ϕe(r)\phi_{e}(\mathbf{r})ϕe(r) ,它表示射频激发过程中带来的相位移动,这会在相位编码的时候再次介绍。这里仅需记住,射频激发会有额外相移即可。
将∣Mxy(r,0+)∣eiϕe(r)=Mxy(r,0+)|M_{xy}(\mathbf{r},0+)|e^{i\phi_{e}(\mathbf{r})}=M_{xy}(\mathbf{r},0+)∣Mxy(r,0+)∣eiϕe(r)=Mxy(r,0+)代入可进一步简化为
Mxy(r,t)=Mxy(r,0+)e−t/T2(r)e−iω(r)tM_{xy}(\mathbf{r},t) = M_{xy}(\mathbf{r},0+)e^{-t/T_{2}(\mathbf{r})}e^{-i\omega(\mathbf{r}) t} Mxy(r,t)=Mxy(r,0+)e−t/T2(r)e−iω(r)t
然后利用接收线圈(将变化的横向宏观磁化强度转化为感生电压)+相敏检测技术(利用解调技术将感应电压中的有效信号从频率ω(r)\omega(\mathbf{r})ω(r)搬移到基带频率Δω(r)\Delta\omega(\mathbf{r})Δω(r): ω(r)→demoduled−ω0Δω(r)\omega(\mathbf{r})\xrightarrow{demoduled-\omega_{0}}\Delta\omega(\mathbf{r})ω(r)demoduled−ω0Δω(r),)+正交检测(I,QI,QI,Q 双路同时检测确定旋转方向),最后对空间的任意 r\mathbf{r}r 进行积分,我们得到了式:
S(t)=ω0∫object∣Br,xy(r)∣∣Mxy(r,0+)∣e−t/T2(r)e−i[Δω(r)t−ϕe(r)+ϕr(r)−π/2]dr\begin{align*} S(t)=\omega_{0}\int_{\text{object}}|B_{r,xy}(\mathbf{r})||M_{xy}(\mathbf{r},0+)|e^{-t/T_{2}(\mathbf{r})} \\ e^{-i[\Delta\omega(\mathbf{r})t-\phi_{e}(\mathbf{r})+\phi_{r}(\mathbf{r})-\pi/2]}d\mathbf{r} \end{align*} S(t)=ω0∫object∣Br,xy(r)∣∣Mxy(r,0+)∣e−t/T2(r)e−i[Δω(r)t−ϕe(r)+ϕr(r)−π/2]dr
上式中,ω(r)=ω0+Δω(r)\omega(\mathbf{r})=\omega_0+\Delta\omega(\mathbf{r})ω(r)=ω0+Δω(r),ω0\omega_0ω0 是PSD的解调信号的频率,ω(r)\omega(\mathbf{r})ω(r) 是空间位置 r\boldsymbol{r}r处的横向宏观磁化自由进动频率。**上述相敏检测对感生电压的处理,在数学上就是从实验室系观察转换到了旋转坐标系下去观察,解调信号的角频率,正是旋转坐标系相对实验室坐标系的转换。
如果是在旋转坐标系下(角速度为ω0\omega_{0}ω0)去观测该空间位置 r\mathbf{r}r 处的x′y′x'y'x′y′方向的横向分量 Mx′y′(r,t)M_{x'y'}(\mathbf{r},t)Mx′y′(r,t)(旋转坐标系下的复数形式),它们之间的转化如下:
Mx′y′(r,t)=e−iω0tMxy(r,t)=Mxy(r,0+)e−t/T2(r)e−iΔω(r)tM_{x'y'}(\mathbf{r},t) =e^{-i\omega_0t}M_{xy}(\mathbf{r},t)= M_{xy}(\mathbf{r},0+)e^{-t/T_{2}(\mathbf{r})}e^{-i\Delta \omega(\mathbf{r}) t} Mx′y′(r,t)=e−iω0tMxy(r,t)=Mxy(r,0+)e−t/T2(r)e−iΔω(r)t
将∣Br,xy(r)∣e−iϕr(r)=Br,xy∗(r),Mx′y′(r,t)|B_{r,xy}(\mathbf{r})|e^{-i\phi_{r}(\mathbf{r})}=B_{r,xy}^{*}(\mathbf{r}),M_{x'y'}(\mathbf{r},t)∣Br,xy(r)∣e−iϕr(r)=Br,xy∗(r),Mx′y′(r,t) 代入上式S(t)S(t)S(t),可进一步化简为
S(t)=ω0eiπ/2∫objectBr,xy∗(r)Mx′y′(r,t)dr\begin{align*} S(t)=\omega_{0}e^{i\pi/2}\int_{\text{object}}B_{r,xy}^{*}(\mathbf{r})M_{x'y'}(\mathbf{r},t)d\mathbf{r} \end{align*} S(t)=ω0eiπ/2∫objectBr,xy∗(r)Mx′y′(r,t)dr
这里面包含了:
- ω0\omega_{0}ω0:它既是相敏检测用于解调的参考信号的频率,同时也是实验室坐标系和旋转坐标系之间的转动角速度。
- ∣Br,xy(r)∣e−iϕr(r)=Br,xy∗(r)|B_{r,xy}(\mathbf{r})|e^{-i\phi_{r}(\mathbf{r})}=B_{r,xy}^{*}(\mathbf{r})∣Br,xy(r)∣e−iϕr(r)=Br,xy∗(r):线圈在空间位置 r\boldsymbol{r}r 处的灵敏度
- Mx′y′(r,t)M_{x'y'}(\mathbf{r},t)Mx′y′(r,t):旋转坐标系下 x′y′x'y'x′y′ 平面的横向宏观磁化矢量的时空演化
如果我们进一步假设线圈在整个空间的灵敏度是均匀的,那么上式还可以进一步简化,同时忽略缩放项ω0eiπ/2\omega_{0}e^{i\pi/2}ω0eiπ/2
S(t)=∫objectMx′y′(r,t)dr\begin{align*} S(t)=\int_{\text{object}}M_{x'y'}(\mathbf{r},t)d\mathbf{r} \end{align*} S(t)=∫objectMx′y′(r,t)dr
可以看到,最终的探测信号就是:
旋转坐标系下观测到的横向宏观磁化强度的时空演变的累积
下面举个例子
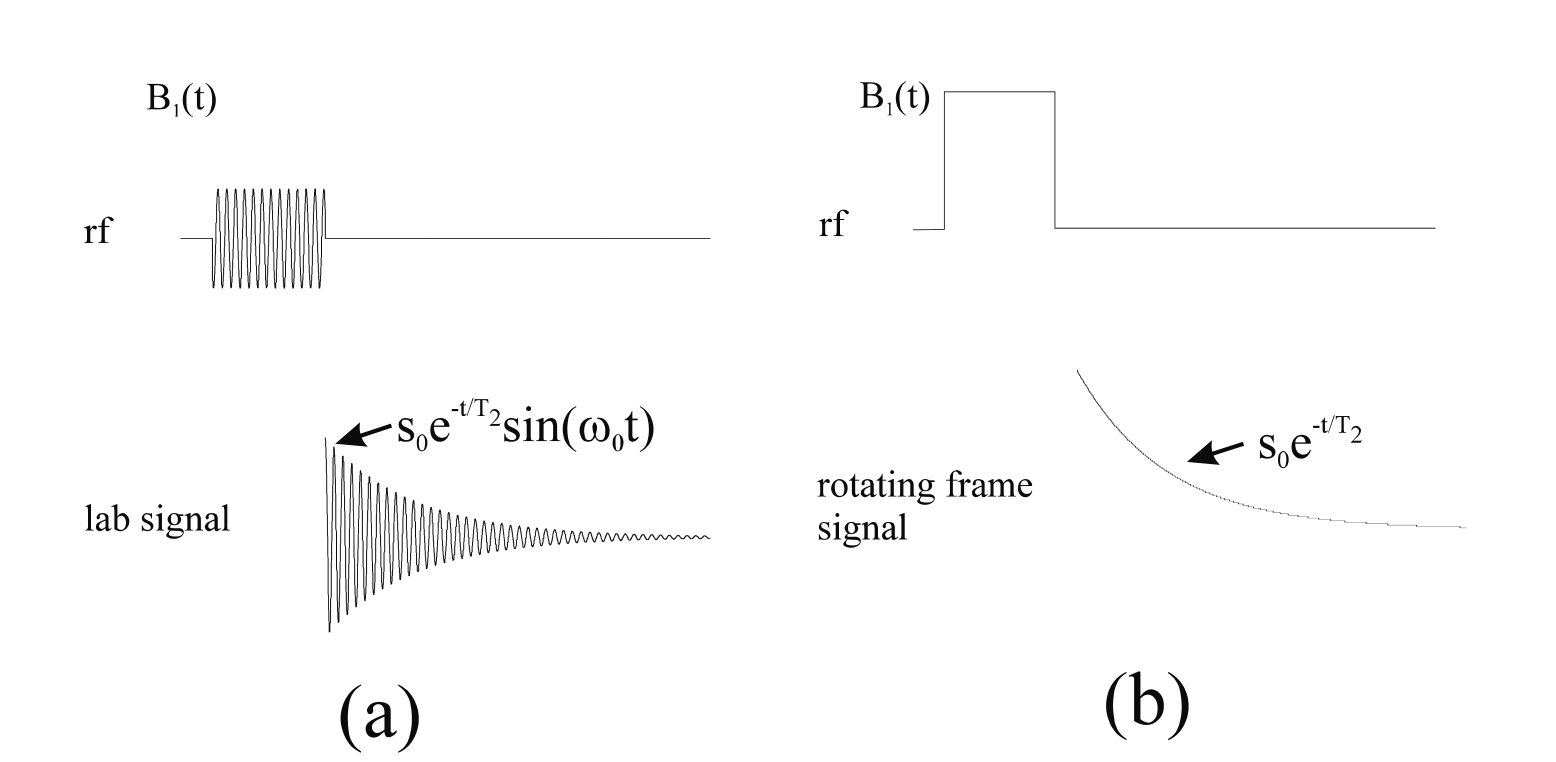
在上图中展示了在实验室坐标系和旋转坐标系下去观测射频信号和探测信号的不同之处:
(a) 在实验室坐标下:射频发射场(图中的rf)以频率 ω\omegaω 振荡,所有自旋以相同拉莫尔频率 ω\omegaω 进动时,在实验室坐标系中观察线圈上感生电压信号(图中震荡衰减信号);
(b) 同一实验,但在拉莫尔旋转坐标系下观察:旋转坐标系中的射频场(图中的rf)处于“静止”状态,旋转坐标系下观察线圈上感生电压信号(图中指数衰减信号,高频的震荡被解调抵消),就等价于对线圈上的感生电压进行PSD解调,这里就是为了说明:解调后信号相当于从实验室坐标系转换到旋转坐标系下去观测。
基本假设
在继续推导FID之前,先提出以下三个基本假设:
-
瞬时射频脉冲:假设射频(RF)脉冲是瞬间施加的,因此脉冲间隔被视为零。除非需要精确的信号发生时间,否则在实践中通常不考虑有限的脉冲间隔。
-
理想激励与接收:忽略激励和接收过程中的任何不完善之处。因此,省略了由于失谐效应和非均匀 B1B_1B1 加权所引起的相移,同时接收线圈的灵敏度 Br,xy∗(r)B_{r,xy}^{*}(\mathbf{r})Br,xy∗(r) 在空间中是均匀的。在此假设下,可以使用简化后的信号表达式(3.150)
S(t)=∫objectMxy(r,0)e−t/T2(r)e−iΔω(r)tdr(3.150)S(t)=\int_{\text{object}}M_{xy}(\mathbf{r},0)\textcolor{red}{e^{-t/T_{2}(\mathbf{r})}}e^{-i\Delta\omega(\mathbf{r})t}d\mathbf{r}\tag {3.150} S(t)=∫objectMxy(r,0)e−t/T2(r)e−iΔω(r)tdr(3.150) -
符号简化:为了符号上的便利,将 Eq. (3.150) 中的频率偏移量 Δω\Delta\omegaΔω 替换为 ω\omegaω。现在,ω\omegaω 代表旋转坐标系中的进动频率。但是这一步符号简化,给后面的分析带来了很多误导,我们需要回忆起一个关键的信息,那就是线圈解调后的探测信号S(t)S(t)S(t)是不含高频的射频频率的。
基于这些假设,探测信号表达式转化为:
S(t)=∫objectMxy(r,0+)e−t/T2(r)e−iω(r)tdr(4.1)S(t) = \int_{\text{object}} M_{xy}(\mathbf{r}, 0+) \, e^{-t/T_2(\mathbf{r})} e^{-i\omega(\mathbf{r})t} \, d\mathbf{r} \tag {4.1} S(t)=∫objectMxy(r,0+)e−t/T2(r)e−iω(r)tdr(4.1)
- S(t)S(t)S(t) 是接收到的时域信号,即自由感应衰减(FID)信号。
- Mxy(r,0+)M_{xy}(\mathbf{r}, 0+)Mxy(r,0+) :在空间点 r\mathbf{r}r 处的自旋团,在射频脉冲结束后瞬间 (t=0+t=0+t=0+) 的横向磁化强度,已经包含了射频相移项 eiϕe(r)e^{i\phi_{e}(\mathbf{r})}eiϕe(r)
- e−t/T2(r)e^{-t/T_2(\mathbf{r})}e−t/T2(r) :在空间点 r\mathbf{r}r 处的自旋团根据横向弛豫时间 T2(r)T_2(\mathbf{r})T2(r) 而导致的信号指数衰减。
- e−iω(r)te^{-i\omega(\mathbf{r})t}e−iω(r)t :在空间点 r\mathbf{r}r 处的自旋团在旋转坐标系中的进动频率(基带频率)
- ∫objectdr\int_{\text{object}} d\mathbf{r}∫objectdr 表示信号是物体内所有空间点贡献的总和。
对于一个非均匀的自旋系统,我们引入一个自旋频谱密度函数 ρ(ω)\rho(\omega)ρ(ω) 来表征其频率分布,注意这里的 ω\omegaω 实际上是频率偏移量 Δω\Delta\omegaΔω ,它表示在拉莫尔旋转坐标系下观察到进动频率,也就是与拉莫尔进动频率的偏移量。这里的 ω=0\omega = 0ω=0 其实代表着在实验室坐标系下的 ω0\omega_0ω0。后面遇到模棱两可的地方,还会再进一步明确。
dM(ω)=ρ(ω)dω(4.2)dM(\omega) = \rho(\omega) \, d\omega \tag {4.2} dM(ω)=ρ(ω)dω(4.2)
M=∫−∞∞ρ(ω)dω(4.3)M = \int_{-\infty}^{\infty} \rho(\omega) \, d\omega \tag {4.3} M=∫−∞∞ρ(ω)dω(4.3)
其中:
- dM(ω)dM(\omega)dM(ω) 代表频率在 [ω,ω+dω][\omega, \omega+d\omega][ω,ω+dω] 区间内的所有“等色散体”的净磁化强度。"等色散体"是指所有具有相同共振频率的自旋集合,注意这里的 ω\omegaω 不是原子核的共振频率,而是在拉莫尔旋转坐标系下观测到的“剩余”进动频率。
- 公式 (4.2) :频谱密度函数 ρ(ω)\rho(\omega)ρ(ω) 描述了净磁化强度在频率 ω\omegaω 处的分布密度
- 公式 (4.3) :对所有频率的 ρ(ω)\rho(\omega)ρ(ω) 进行积分,即可得到整个样品的总磁化强度 MMM。
将 ρ(ω)\rho(\omega)ρ(ω) 代入公式 (4.1),可以将其从空间积分转换为频率积分。
S(t)=∫−∞∞ρ(ω)e−t/T2(ω)e−iωtdω(4.4)S(t) = \int_{-\infty}^{\infty} \rho(\omega) \, e^{-t/T_2(\omega)} e^{-i\omega t} \, d\omega \tag {4.4} S(t)=∫−∞∞ρ(ω)e−t/T2(ω)e−iωtdω(4.4)
在公式 (4.1) 中,信号是空间位置 r\mathbf{r}r 的函数,每个位置对应一个频率 ω(r)\omega(\mathbf{r})ω(r) 和一个弛豫时间 T2(r)T_2(\mathbf{r})T2(r)。通过引入 ρ(ω)\rho(\omega)ρ(ω),我们将视角从“空间”转换到了“频率”。现在,我们不再关心磁化强度在空间中的哪个位置,只关心它处于哪个频率。 因此,积分变量从空间元 drd\mathbf{r}dr 变为频率元 dωd\omegadω。被积函数变为:在频率 ω\omegaω 附近的磁化强度频谱密度函数 ρ(ω)\rho(\omega)ρ(ω),乘以该频率分量对应的弛豫项 e−t/T2(ω)e^{-t/T_2(\omega)}e−t/T2(ω) 和进动项 e−iωte^{-i\omega t}e−iωt
需要特别注意,ρ(ω)\rho(\omega)ρ(ω) 并非时域信号 S(t)S(t)S(t) 的傅里叶频谱。
S(t)=12π∫−∞∞ρ^(ω)e−iωtdω(4.5)S(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \hat{\rho}(\omega) e^{-i\omega t} \, d\omega \tag {4.5} S(t)=2π1∫−∞∞ρ^(ω)e−iωtdω(4.5)
其中:
- 我们使用 ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 来表示时域信号 S(t)S(t)S(t) 的傅里叶频谱。
- 根据傅里叶分析的标准定义,时域信号 S(t)S(t)S(t) 和其频谱 ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 通过傅里叶变换对相关联。式 (4.5) 是逆傅里叶变换的形式,将频谱 ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 转换回时域信号 S(t)S(t)S(t)。
- ρ(ω)\rho(\omega)ρ(ω) 和 ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 的关系:只有当 T2T_2T2 弛豫可以忽略不计时(即 T2→∞T_2 \to \inftyT2→∞),比较式 (4.4) 和式 (4.5) 会发现 ρ(ω)=2πρ^(ω)\rho(\omega) = 2\pi \hat{\rho}(\omega)ρ(ω)=2πρ^(ω)。
- 在存在 T2T_2T2 弛豫的一般情况下,ρ(ω)\rho(\omega)ρ(ω) 是描述样品本身固有属性的物理频谱分布(拉莫尔旋转坐标系下的频率),而 ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 是实际测得的 FID 信号 S(t)S(t)S(t) 经过傅里叶变换后得到的测量频谱。弛豫过程会加宽测量频谱 ρ^(ω)\hat{\rho}(\omega)ρ^(ω)。
对于由 NNN 个共振频率分别为 ωn\omega_nωn 的等色散体组成的自旋系统,其频谱密度函数由 NNN 个位于 ωn\omega_nωn 的狄拉克 δ\deltaδ 函数之和构成。
ρ(ω)=∑n=1NMz,n0δ(ω−(ωn−ω0))(4.6)\rho(\omega) = \sum_{n=1}^{N} M_{z,n}^{0} \, \delta(\omega - (\omega_n\textcolor{red}{-\omega_0})) \tag {4.6} ρ(ω)=n=1∑NMz,n0δ(ω−(ωn−ω0))(4.6)
其中:
- Mz,n0M_{z,n}^{0}Mz,n0 是共振频率为 ωn\omega_nωn 的第 nnn 个等色散体的热平衡磁化强度。
- 狄拉克函数 δ(ω−(ωn−ω0))\delta(\omega - (\omega_n\textcolor{red}{-\omega_0}))δ(ω−(ωn−ω0)) 表示所有磁化强度都精确地集中在频率 (ωn−ω0)(\omega_n\textcolor{red}{-\omega_0})(ωn−ω0) 处。
- 这是一种理想化的模型,例如,可以用于表示一种化学样品中不同化学环境的原子核
当样品被置于一种特殊的、具有洛伦兹型分布(又叫柯西-洛伦兹分布,请参考柯西分布-数学百科)局域场不均匀性的磁场中时,产生的频谱密度函数具有以下形式:
ρ(ω)=Mz0(γΔB0)2(γΔB0)2+(ω−(ω0−ω0))2(4.7)\rho(\omega) = M_{z}^{0} \, \frac{(\gamma \Delta B_0)^2}{(\gamma \Delta B_0)^2 + (\omega - (\omega_0\textcolor{red}{-\omega_0}))^2} \tag {4.7} ρ(ω)=Mz0(γΔB0)2+(ω−(ω0−ω0))2(γΔB0)2(4.7)
其中:
- Mz0M_z^0Mz0 是样品的总热平衡磁化强度。
- ω0\omega_0ω0 是中心的共振频率,也是拉莫尔旋转参考系的角速度。
- γΔB0\gamma \Delta B_0γΔB0 与磁场不均匀性导致的半高宽。
- 这个函数是洛伦兹函数的形式。它描述了当局域场的变化遵循某种统计分布时,自旋频率会分散在一个中心频率 (ω0−ω0)(\omega_0\textcolor{red}{-\omega_0})(ω0−ω0) 附近,形成一个钟形的连续分布。这是一种非常常见的模型,用于描述均匀展宽机制主导下的 NMR 谱线形状。
自由感应衰减 (Free Induction Decays)
自由感应衰减 (FID) 信号产生于单个射频脉冲对核自旋系统的作用。
- “自由” 指的是该信号由宏观磁化矢量 M⃗\vec MM 绕主磁场 B→0\overrightarrow{B}_{0}B0 自由进动 而产生;
- “感应” 表明该信号是基于 法拉第电磁感应定律 产生的;
- “衰减” 则反映了信号幅度随时间 特征性地减弱。
FID 信号是脉冲激发后自旋系统产生的最基础的瞬态信号形式。后续要介绍"射频回波,梯度回波"等其他类型磁共振 (MR) 信号的都是基于此信号的衍生。
让我们回顾一下之前的内容:
物体在外部磁场 B⃗0\vec B_{0}B0 处于热平衡态时,其宏观磁化矢量在xyxyxy方向的横向分量为0,仅剩 zzz 方向的纵向分量为 Mz0M_z^0Mz0 ,它也可以表示成频谱密度对频率的积分:
Mz0=∫−∞∞ρ(ω)dωM_z^0 = \int_{-\infty}^{\infty} \rho(\omega) \, d\omega Mz0=∫−∞∞ρ(ω)dω
一个 α\alphaα 脉冲激发后,t=0+t=0+t=0+ 时刻的 xyxyxy方向的横向分量Mxy(0+)M_{xy}(0+)Mxy(0+)为
Mxy(0+)=sinα⋅Mz0=sinα∫−∞∞ρ(ω)dωM_{xy}(0+) = sin \alpha \cdot M_z^0 = sin \alpha \int_{-\infty}^{\infty} \rho(\omega) \, d\omega Mxy(0+)=sinα⋅Mz0=sinα∫−∞∞ρ(ω)dω
将其代入带式(4.4),可得 α\alphaα 脉冲激发后的FID信号表达式:
S(t)=sinα∫−∞∞ρ(ω)e−t/T2(ω)e−iωtdωt≥0(4.12)S(t) = \sin\alpha \int_{-\infty}^{\infty} \rho(\omega) e^{-t/T_{2}(\omega)} e^{-i\omega t} \, d\omega \qquad t \geq 0 \tag {4.12} S(t)=sinα∫−∞∞ρ(ω)e−t/T2(ω)e−iωtdωt≥0(4.12)
其中:
- e−iωte^{-i\omega t}e−iωt 代表在宏观磁化分量在旋转坐标系下的进动,注意之前将Δω\Delta\omegaΔω 换成了ω\omegaω
磁场均匀分布下的“单色散”物质的FID
若自旋系统仅有一个频谱成分,我们称其为“单色散”物质,水在MRI中只有一个尖锐的共振峰,是典型的“单色散”物质。参考(4.6) 将其转化为“单色散”(仅有一个共振频率: ω0\omega_0ω0)的形式
ρ(ω)=Mz0δ(ω−(ω0−ω0))\rho(\omega) = M_{z}^{0} \, \delta(\omega - (\omega_0\textcolor{red}{-\omega_0})) ρ(ω)=Mz0δ(ω−(ω0−ω0))
将 ρ(ω)\rho(\omega)ρ(ω) 代入到 (4.12),得到FID 信号的表达式为:
S(t)=Mz0sinαe−t/T2e−i(ω0−ω0)tt≥0(4.13)S(t) = M_{z}^{0} \sin\alpha \, e^{-t/T_{2}} e^{-i(\omega_0\textcolor{red}{-\omega_0})t} \qquad t \geq 0 \tag {4.13} S(t)=Mz0sinαe−t/T2e−i(ω0−ω0)tt≥0(4.13)
解释:
- Mz0M_z^0Mz0 是热平衡状态下的宏观磁化强度。
- 此时 ρ(ω)\rho(\omega)ρ(ω) 是狄拉克函数 δ(ω−ω0)\delta(\omega - \omega_0)δ(ω−ω0),积分后得到单一频率项。
- 衰减项 e−t/T2e^{-t/T_2}e−t/T2 是纯指数形式(假设 T2T_2T2 为常数)。
- e−i(ω0−ω0)te^{-i(\omega_0\textcolor{red}{-\omega_0})t}e−i(ω0−ω0)t 中,前者ω0\omega_{0}ω0是共振频率,后者 ω0\textcolor{red}{\omega_0}ω0 是用于对线圈的感应电压进行PSD的解调所用的参考信号的频率。这里假设它和共振频率一致(实际上很难完全一致)。原书中并没有上述红色字体,这与实际并不相符:FID信号中并不存在高频信号,因为PSD已经将信号从高频“搬移”到基带。如果一致的话,该项简化为1.
下面用MATLAB脚本,来分析一下,当PSD解调和共振频率存在频率差时的FID图像
clear;
clc;
delta_w = [1e3,100,0];
T2 = 30e-3;
t = 0:1e-6:5*T2;
FID1 = exp(-1*t/T2).*cos(delta_w(1)*t);
FID2 = exp(-1*t/T2).*cos(delta_w(2)*t);
FID3 = exp(-1*t/T2).*cos(delta_w(3)*t);figure;
plott(1) = plot(t,FID1,'displayname',['FID', '\Delta\omega =',num2str(delta_w(1))]);
hold
plott(2) = plot(t,FID2,'displayname',['FID', '\Delta\omega =',num2str(delta_w(2))]);
plott(3) = plot(t,FID3,'displayname',['FID', '\Delta\omega =',num2str(delta_w(3))]);
legend(plott);
grid on;
xlabel('Time: s')
ylabel('FID Strength')
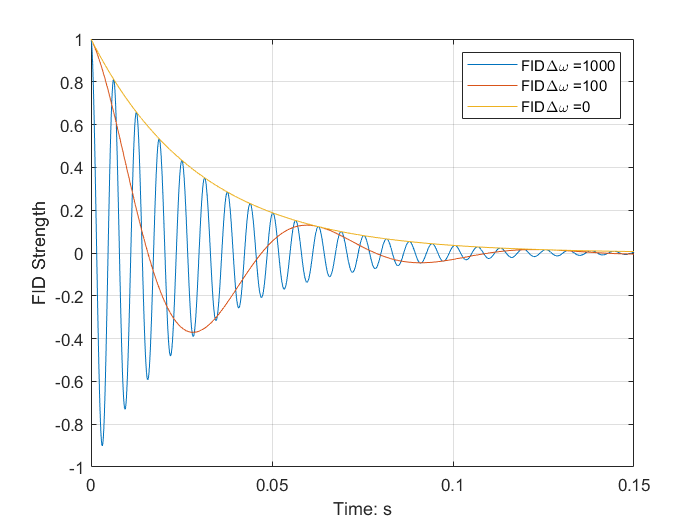
FID 信号在 t=0t=0t=0 时达到最大振幅,FID的最大值同时取决于翻转角以及热平衡态下的宏观磁化强度:
Af=sinα∫−∞∞ρ(ω)dω=Mz0sinα(4.14)A_f = \sin\alpha \int_{-\infty}^{\infty} \rho(\omega) \, d\omega = M_z^0 \sin\alpha \tag {4.14} Af=sinα∫−∞∞ρ(ω)dω=Mz0sinα(4.14)
如果对式(4.13)的FID信号进行频谱分析
ρ^(ω)=F{S(t)}=∫0∞Afe−t/T2e−i[ω0−ω0]te−iωtdt=AfT21+T22(ω+ω0−ω0)2−iAfT22(ω+ω0−ω0)1+T22(ω+ω0−ω0)2\begin{aligned} \hat{\rho}(\omega) & = \mathcal{F}\{S(t)\} = \int_{0}^{\infty} A_f e^{-t / T_{2}} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t} e^{-i \omega t} \, dt \\ & = \frac{A_f T_{2}}{1 + T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} - i \frac{A_f T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})}{1 + T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} \end{aligned} ρ^(ω)=F{S(t)}=∫0∞Afe−t/T2e−i[ω0−ω0]te−iωtdt=1+T22(ω+ω0−ω0)2AfT2−i1+T22(ω+ω0−ω0)2AfT22(ω+ω0−ω0)
注意:ρ^(ω)≠ρ(ω)\hat{\rho}(\omega) \neq \rho(\omega)ρ^(ω)=ρ(ω),前者是S(t)S(t)S(t)信号的频谱分布,在本例中它具备洛伦兹分布,其半高宽为1T2\frac{1}{T_2}T21,后者是宏观磁化强度的频谱密度函数,在本例中是一个单一点频谱(半高宽为0,单一频率)。
因此横向弛豫项e−t/T2e^{-t / T_{2}}e−t/T2的存在,就会让频谱分布ρ^(ω)\hat{\rho}(\omega)ρ^(ω)在宏观磁化强度的频谱密度函数ρ(ω)\rho(\omega)ρ(ω)的基础上加宽了半高宽为1T2\frac{1}{T_2}T21,T2T_2T2越小,半高宽越宽;只有当 T2T_2T2 无穷大时,两者才是等价的。
磁场不均匀分布下的“单色散”物质的FID
FID信号的衰减速率与其内在的频谱分布密切相关。对于单色散物质,FID信号呈现出特征性的T2T_2T2衰减,如公式(4.13)所示。这种现象发生在样品及其所处磁场均达到完美均匀的理想条件下。当磁场存在不均匀性时,FID信号的衰减速率会显著加快。
为说明这一现象,假设存在两组质子团(1H^1H1H),分别处于1 T 和1.01 T的磁场中。它们的进动频率分别为42 MHz和42.42 MHz。在1微秒的时间内,第一组质子团完成了42次旋转,而第二组质子团完成了42.42次旋转。在此短暂时间范围内,第一组较第二组滞后近半圈(0.42圈),即两者相位差接近180°。当我们考察大量的质子时,此过程将建立随机相位关系。其结果是各组磁矩相互抵消,导致横向宏观磁化强度的弛豫加快。此时的衰减时间常数为 ,它与T2T_2T2是不同的:
- T2T_2T2 是因为自旋-晶格、自旋-自旋相互作用引入的,是随机的,不可恢复的。
- T2∗T_2^*T2∗ 是因为主磁场B0B_0B0 不均匀导致的,它是可恢复的,在射频回波中重点再介绍一下。
若磁场不均匀性呈现频谱呈洛伦兹分布(参考式 4.7),此时的频谱密度函数ρ(ω)\rho(\omega)ρ(ω)也是呈洛伦兹线性,其半高宽是γΔB0\gamma \Delta B_0γΔB0,中心频率是ω0\omega_0ω0,如下:
ρ(ω)=Mz0(γΔB0)2(γΔB0)2+(ω−(ω0−ω0))2(4.7)\rho(\omega) = M_{z}^{0} \, \frac{(\gamma \Delta B_0)^2}{(\gamma \Delta B_0)^2 + (\omega - (\omega_0\textcolor{red}{-\omega_0}))^2} \tag {4.7} ρ(ω)=Mz0(γΔB0)2+(ω−(ω0−ω0))2(γΔB0)2(4.7)
将 ρ(ω)\rho(\omega)ρ(ω) 代入到 (4.12),得到FID 信号的表达式为:
S(t)=sinα∫−∞∞Mz0(γΔB0)2(γΔB0)2+(ω−(ω0−ω0))2e−t/T2e−iωtdω=sinα∫−∞∞[Mz0(γΔB0)2(γΔB0)2+ω2e−iωtdω]e−t/T2e−i[ω0−ω0]t=πMz0γΔB0sinαe−γΔB0te−t/T2e−i[ω0−ω0]t=πMz0γΔB0sinαe−t/T2∗e−i[ω0−ω0]tt≥0\begin{align*} S(t) &= \sin\alpha \int_{-\infty}^{\infty} M_z^0 \frac{(\gamma \Delta B_0)^2}{(\gamma \Delta B_0)^2 + (\omega - (\omega_0\textcolor{red}{-\omega_0}))^2} e^{-t/T_2} e^{-i\omega t} \, d\omega \\ &= \sin\alpha \int_{-\infty}^{\infty} \left[ M_z^0 \frac{(\gamma \Delta B_0)^2}{(\gamma \Delta B_0)^2 + \omega^2} e^{-i\omega t} \, d\omega \right] e^{-t/T_2} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t} \\ &= \pi M_z^0 \gamma \Delta B_0 \sin\alpha \, e^{-\gamma \Delta B_0 t} e^{-t/T_2} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t} \\ &= \pi M_z^0 \gamma \Delta B_0 \sin\alpha \, e^{-t/T_2^*} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t} \qquad t \geq 0 \tag {4.15} \end{align*} S(t)=sinα∫−∞∞Mz0(γΔB0)2+(ω−(ω0−ω0))2(γΔB0)2e−t/T2e−iωtdω=sinα∫−∞∞[Mz0(γΔB0)2+ω2(γΔB0)2e−iωtdω]e−t/T2e−i[ω0−ω0]t=πMz0γΔB0sinαe−γΔB0te−t/T2e−i[ω0−ω0]t=πMz0γΔB0sinαe−t/T2∗e−i[ω0−ω0]tt≥0(4.15)
推导说明:
-
第三行:利用洛伦兹函数的傅里叶变换性质 ∫−∞∞a2a2+ω2e−iωtdω=πae−a∣t∣\int_{-\infty}^{\infty} \frac{a^2}{a^2 + \omega^2} e^{-i\omega t} \, d\omega = \pi a e^{-a|t|}∫−∞∞a2+ω2a2e−iωtdω=πae−a∣t∣(其中 a=γΔB0a = \gamma \Delta B_0a=γΔB0)。
-
第四行:定义有效衰减时间常数 T2∗T_2^*T2∗,它和T2T_2T2的关系如下:
1T2∗=1T2+γΔB0(4.16)\frac{1}{T_2^*} = \frac{1}{T_2} + \gamma \Delta B_0 \tag {4.16} T2∗1=T21+γΔB0(4.16) -
γΔB0\gamma \Delta B_0γΔB0 是磁场不均匀性导致的额外衰减速率(γ\gammaγ 为旋磁比,ΔB0\Delta B_0ΔB0 为磁场不均匀度)。
-
T2∗T_2^*T2∗ 是实际观测到的信号衰减时间常数,满足 T2∗≤T2T_2^* \leq T_2T2∗≤T2。
FID 信号在 t=0t=0t=0 时达到最大振幅,FID的最大值同时取决于翻转角以及热平衡态下的宏观磁化强度:
Af=πMz0γΔB0sinαA_f = \pi M_z^0 \gamma \Delta B_0 \sin\alpha Af=πMz0γΔB0sinα
如果对式(4.15)的FID信号进行频谱分析
ρ^(ω)=F{S(t)}=∫0∞Afe−t/T2∗e−i[ω0−ω0]te−iωtdt=AfT2∗1+T2∗2(ω+ω0−ω0)2−iAfT2∗2(ω+ω0−ω0)1+T2∗2(ω+ω0−ω0)2\begin{aligned} \hat{\rho}(\omega) & = \mathcal{F}\{S(t)\} = \int_{0}^{\infty} A_f e^{-t / T_{2}^*} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t} e^{-i \omega t} \, dt \\ & = \frac{A_f T_{2}^*}{1 + {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} - i \frac{A_f {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})}{1 + {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} \end{aligned} ρ^(ω)=F{S(t)}=∫0∞Afe−t/T2∗e−i[ω0−ω0]te−iωtdt=1+T2∗2(ω+ω0−ω0)2AfT2∗−i1+T2∗2(ω+ω0−ω0)2AfT2∗2(ω+ω0−ω0)
可以看到ρ^(ω)\hat{\rho}(\omega)ρ^(ω) 的中心频率也在ω0−ω0\omega_0\textcolor{red}{-\omega_{0}}ω0−ω0,其半高宽是1T2∗\frac{1}{T_2^*}T2∗1。相比ρ(ω)\rho(\omega)ρ(ω) 半高宽是γΔB0\gamma \Delta B_0γΔB0,它也增大了1T2\frac{1}{T_2}T21。
对比总结:
| 均匀磁场 1H^1H1H | 非均匀洛伦在磁场 1H^1H1H | |
|---|---|---|
| ρ(ω)\rho(\omega)ρ(ω) | ρ(ω)=Mz0δ(ω−(ω0−ω0))\rho(\omega) = M_{z}^{0} \, \delta(\omega - (\omega_0\textcolor{red}{-\omega_0}))ρ(ω)=Mz0δ(ω−(ω0−ω0)) | ρ(ω)=Mz0(γΔB0)2(γΔB0)2+(ω−(ω0−ω0))2\rho(\omega) = M_{z}^{0} \, \frac{(\gamma \Delta B_0)^2}{(\gamma \Delta B_0)^2 + (\omega - (\omega_0\textcolor{red}{-\omega_0}))^2}ρ(ω)=Mz0(γΔB0)2+(ω−(ω0−ω0))2(γΔB0)2 |
| ρ(ω)\rho(\omega)ρ(ω)半高宽 | 0 | γΔB0\gamma \Delta B_0γΔB0 |
| S(t)S(t)S(t) | Mz0sinαe−t/T2e−i[ω0−ω0]tM_{z}^{0} \sin\alpha \, e^{-t/T_{2}} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t}Mz0sinαe−t/T2e−i[ω0−ω0]t | πMz0γΔB0sinαe−t/T2∗e−i[ω0−ω0]t\pi M_z^0 \gamma \Delta B_0 \sin\alpha \, e^{-t/T_2^*} e^{-i[\omega_{0}\textcolor{red}{-\omega_{0}}]t}πMz0γΔB0sinαe−t/T2∗e−i[ω0−ω0]t |
| ρ^(ω)\hat{\rho}(\omega)ρ^(ω) | AfT21+T22(ω+ω0−ω0)2−iAfT22(ω+ω0−ω0)1+T22(ω+ω0−ω0)2\frac{A_f T_{2}}{1 + T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} - i \frac{A_f T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})}{1 + T_{2}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}}1+T22(ω+ω0−ω0)2AfT2−i1+T22(ω+ω0−ω0)2AfT22(ω+ω0−ω0) | AfT2∗1+T2∗2(ω+ω0−ω0)2−iAfT2∗2(ω+ω0−ω0)1+T2∗2(ω+ω0−ω0)2\frac{A_f T_{2}^*}{1 + {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}} - i \frac{A_f {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})}{1 + {T_{2}^*}^{2} (\omega + \omega_{0}\textcolor{red}{-\omega_{0}})^{2}}1+T2∗2(ω+ω0−ω0)2AfT2∗−i1+T2∗2(ω+ω0−ω0)2AfT2∗2(ω+ω0−ω0) |
| ρ^(ω)\hat{\rho}(\omega)ρ^(ω)半高宽 | 1T2\frac{1}{T_2}T21 | 1T2+γΔB0\frac{1}{T_2} + \gamma \Delta B_0T21+γΔB0 |
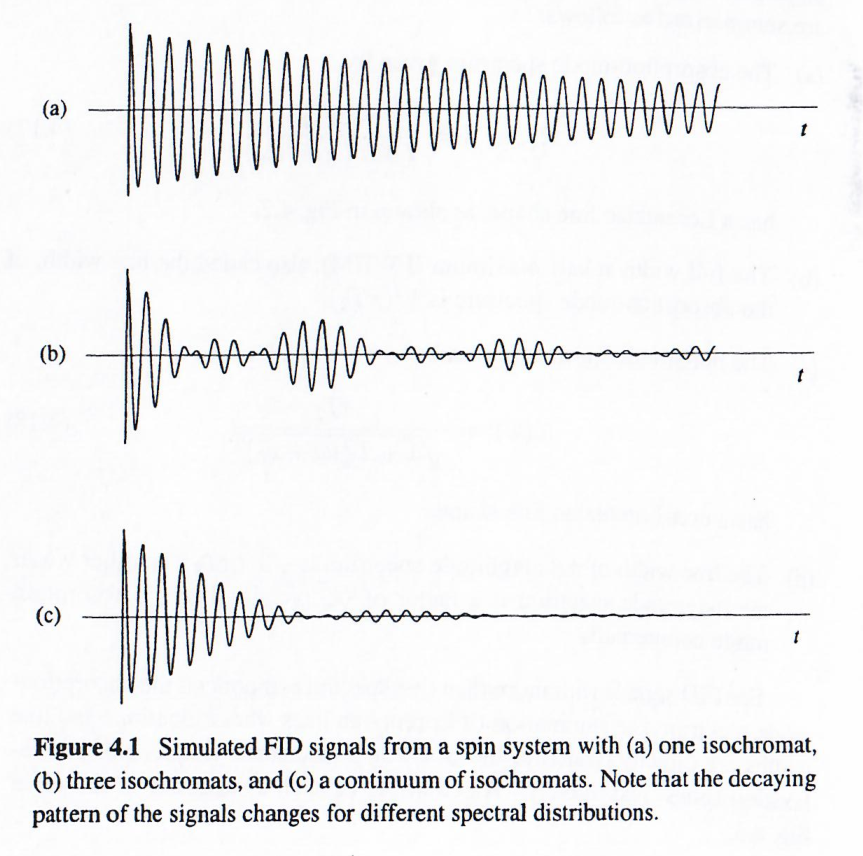
尽管式(4.16)在磁共振文献中被广泛使用,但其仅严格适用于洛伦兹型谱密度函数。对于其他类型的谱密度函数,自由感应衰减(FID)信号的包络函数并非指数函数,此时应将 T2∗T_2^*T2∗ 解释为近似指数函数的有效时间常数。为说明不同谱分布对FID信号特性的影响,下图展示了若干示例。