Counting Towers (动态规划)

题目：

思路：

化繁为简

注意到其实任意情况我们都能分成 2*n + m 的格子形式，所以考虑拆解

我们定义 f[i][1/2] 为第 i 层是放了两个单个还是放了一个整个，那么分析两种情况

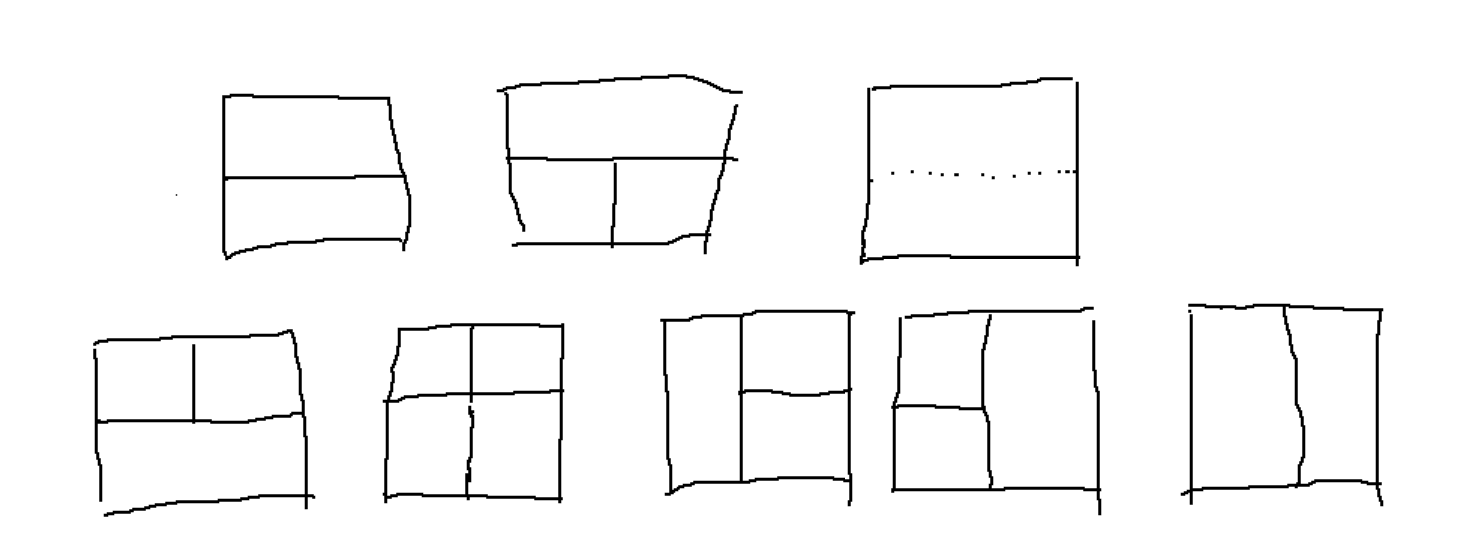
①. f[i][1]

此时上面放了一个 1*2 ，那么就是有上面的三种情况，可以发现，其可以表示为

f[i][1] = f[i-1][1] * 2 + f[i-1][2]

②. f[i][2]

同理可以看到有以下五种情况，直接转移就有

f[i][2] = f[i-1][2]*4 + f[i-1][1]

其余情况都可以用以上组合排列组合得到，同理其余情况也是如上转移

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
const int MOD = 1e9 + 7;
int f[1000006][2]; // 建造到了第 i 层，且这一层放了一块还是两块void add(int &a, int b)
{a = (a + b) % MOD;
}void init()
{f[1][1] = 1;f[1][2] = 1;for (int i = 2; i <= 1000000; i++){add(f[i][1], f[i - 1][1] * 2);add(f[i][1], f[i - 1][2]);add(f[i][2], f[i - 1][1]);add(f[i][2], f[i - 1][2] * 4);}
}void solve()
{int n;cin >> n;cout << (f[n][1] + f[n][2]) % MOD << endl;
}signed main()
{init();ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}