水题记录1.8

luogu14011 [POCamp 2023] 珿求 / bootfall

link

题目：

考虑使用 DP。

记 $f[i]$ 表示防守为 $i$ 的情况下进攻的最大值。

然后就是喜闻乐见的分讨。

考虑防守为 $x$，对面队伍进攻为 $A$，防守为 $D$。

考虑 $x\ge A$，说明对面无法进球，此时若存在 $j>x,f[j]>D$，说明可以赢。这个可以用后缀 $\max$ 维护。

考虑 $x\le A$，此时对面进了 $A-x$ 个球，积分为 $\max (f[x]-D,0)-A+x$，积分的正负决定我们的输赢。

但是你可以发现，对于 $f[x]\le D$，积分仍未负，$\max$ 没影响，若 $f[x]>D$，取 $\max$ 仍然没有影响，所以可以直接去掉。

那么就是找最大的 $x+f[x]$，并和 $A+D$ 比大小即可。

接下来是平局，要么存在 $x\ge A,f[x]$ 合法，要么存在 $x\le A,x+f[x]=A+D$，否则就输了。

那么这题就做完了：

赛时没想那么多，直接滚动数组，所以 $f$ 是两维的。

#include<bits/stdc++.h>
using namespace std;
const int N=4e2+1,M=1.6e5;
int f[2][M],n,a[N],d[M],f1[M],f2[M];
signed main(){cin>>n;memset(f,-0x3f3f3f3f,sizeof f);f[0][0]=0;for(int i=1;i<=n;i++){cin>>a[i]>>d[i];int np=i&1,pp=np^1;for(int j=0;j<M;j++)f[np][j]=-0x3f3f3f3f;for(int j=0;j<M;j++){f[np][j]=max(f[np][j],f[pp][j]+a[i]);int k=min(M-1,j+d[i]);f[np][k]=max(f[np][k],f[pp][j]);}}int id=n&1;f1[M-1]=f[id][M-1];for(int i=M-2;i>=0;i--){f1[i]=max(f1[i+1],f[id][i]);}f2[0]=f[id][0];for(int i=1;i<M;i++)f2[i]=max(f2[i-1],f[id][i]+i);int q;cin>>q;int c1=0,c2=0,c3=0;while(q--){int A,D;cin>>A>>D;if(f1[A]>D){c1++;continue;}if(f2[A]-A-D>0){c1++;continue;}if(f1[A]>=0||f2[A]-A-D==0)c2++;elsec3++;}cout<<c1<<" "<<c2<<" "<<c3<<"\n";return 0;
}

luogu14013 [POCamp 2023] 送钱 / The Generous Traveler

link

题目：

先说一个结论，对于一个 $v$，每一次取模使它的值改变，则使它值改变的次数为 $\log v$ 级别的。

证明考虑分类模数与 $\frac{v}{2}$ 的大小。

那么可以暴力查找最近的小于等于当前值的值，暴力取模。

可以想到树链剖分，剖分成 $\log n$ 条重链，将询问拆成 $\log n$ 个区间并逐一使用线段树上二分查询，并更改值。

复杂度为 $O(n\log n\log V)$，可以过。

但是你会发现遍历的顺序是重要的，不能交换。

考虑将路径拆成 $x⟶lca,lca⟶y$ 两条路径。

如图：

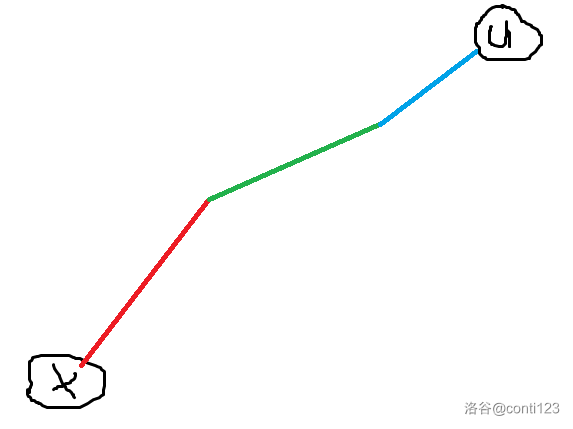
$x$ 经过三条重链到达了 $lca$ $u$，那么这三条链的实际遍历顺序为红，绿，蓝，实际存储顺序也为红，绿，蓝。

但是，我们存储的区间是链顶到链底，和实际顺序相反。

所以你算的时候每个区间从右往左。

同理，如果是 $u$ 到 $y$，你的区间遍历是正的，但是存储是反的，改一下即可。

#define ls x<<1
#define rs x<<1|1
#define mid (l+r>>1)
struct Tr_{vector<int>E[N];int fa[N],dfn[N],d[N],top[N],sz[N],son[N];int idx=0;int a[N],b[N],mi[N<<2];void addE(int x,int y){E[x].push_back(y),E[y].push_back(x);}void dfs(int u,int pa){fa[u]=pa,sz[u]=1,d[u]=d[pa]+1;int o=0;for(int i=0;i<E[u].size();i++){int v=E[u][i];if(v==pa)continue;dfs(v,u);sz[u]+=sz[v];if(sz[v]>o)o=sz[v],son[u]=v;}}void dfs_(int u,int Top){top[u]=Top;dfn[u]=++idx;b[idx]=a[u];if(!son[u])return ;dfs_(son[u],Top);for(int i=0;i<E[u].size();i++){int v=E[u][i];if(v==fa[u]||v==son[u])continue;dfs_(v,v);}}void pushup(int x){mi[x]=min(mi[ls],mi[rs]);}void build(int x,int l,int r){if(l==r){mi[x]=b[l];return ;}build(ls,l,mid);build(rs,mid+1,r);pushup(x);}int ask(int x,int l,int r,int ql,int qr,int k){if(mi[x]>k||ql>qr||qr<l||ql>r)return 1e9;if(l==r)return l;int res=ask(ls,l,mid,ql,qr,k);if(res!=1e9)return res;res=ask(rs,mid+1,r,ql,qr,k);return res;}int ask1(int x,int l,int r,int ql,int qr,int k){if(mi[x]>k||ql>qr||qr<l||ql>r)return 1e9;if(l==r)return l;int res=ask1(rs,mid+1,r,ql,qr,k);if(res!=1e9)return res;res=ask1(ls,l,mid,ql,qr,k);return res;}void calc(int &res,int x,int y){for(int i=x;;){int rrr=ask(1,1,n,i,y,res);if(rrr==1e9)break;res%=b[rrr];i=rrr+1;}}void calc1(int &res,int x,int y){for(int i=y;;){int rrr=ask1(1,1,n,x,i,res);if(rrr==1e9)break;res%=b[rrr];i=rrr-1;}}int LCA(int x,int y){while(top[x]!=top[y]){if(d[top[x]]<d[top[y]]) swap(x,y);x=fa[top[x]];}return d[x]<d[y]?x:y;}int askxy(int x,int y,int k){int lca=LCA(x,y);int res=k;vector<pair<int,int>>l,r;int u=x;while(top[u]!=top[lca]){l.push_back({dfn[top[u]],dfn[u]});u=fa[top[u]];}l.push_back({dfn[lca],dfn[u]});int v=y;while(top[v]!=top[lca]){r.push_back({dfn[top[v]],dfn[v]});v=fa[top[v]];}if(v!=lca)r.push_back({dfn[lca]+1,dfn[v]});reverse(r.begin(),r.end());for(auto [L,R]:l)calc1(res,L,R);for(auto [L,R]:r)calc(res,L,R);return res;}
}A;

luogu11340 [COI 2019] TENIS

link

题目：

考虑可能获胜的，一定是一段区间 $[1,c]$，即所有能获胜的人他的所有排名在这个区间内。

证明考虑若存在一个人能获胜，且他某个某个场地排名 $k>c$，则若某个不能获胜的选手在这个场地排名 $k^{\prime }<k$，那么让这个获胜的人（以及他能打败的人）打完其他对手，这个本来不获胜的人获胜了。

所以可以用 $[l,r)$ 区间刻画一个人的最高排名和最低排名，那么 $c$ 就是最小的，满足所有区间都与 $c$ 不交的值。

这一点可以用线段树区间加减维护（注意右端点）。

那么这题就做完了。

struct fy{int a,b,c;int l(){return min(a,min(b,c));}int r(){return max(a,max(b,c));}
}a[N];
struct Tr_{int mi[N<<2],add[N<<2];void pushup(int x){mi[x]=min(mi[ls],mi[rs]);}void pushdown(int x){if(add[x]!=0){int &Ad=add[x];mi[ls]+=Ad,mi[rs]+=Ad;add[ls]+=Ad,add[rs]+=Ad;Ad=0;}}void upd(int x,int l,int r,int ql,int qr,int k){if(ql>qr)return ;if(ql<=l&&r<=qr){mi[x]+=k,add[x]+=k;return ;}pushdown(x);if(ql<=mid)upd(ls,l,mid,ql,qr,k);if(qr>mid)upd(rs,mid+1,r,ql,qr,k);pushup(x);}int ask(int x,int l,int r){if(l==r)return l;pushdown(x);if(mi[ls]==0)return ask(ls,l,mid);return ask(rs,mid+1,r);}
}A;
signed main(){ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL);cin>>n>>m;for(int i=1;i<=n;i++){int x;cin>>x;a[x].a=i;}for(int i=1;i<=n;i++){int x;cin>>x;a[x].b=i;}for(int i=1;i<=n;i++){int x;cin>>x;a[x].c=i;}for(int i=1;i<=n;i++)A.upd(1,1,n,a[i].l(),a[i].r()-1,1);while(m--){int op,op1,x,y;cin>>op;if(op==1){cin>>x;int res=A.ask(1,1,n);if(a[x].r()<=res)cout<<"DA\n";elsecout<<"NE\n";}else{cin>>op1>>x>>y;A.upd(1,1,n,a[x].l(),a[x].r()-1,-1);A.upd(1,1,n,a[y].l(),a[y].r()-1,-1);if(op1==1)swap(a[x].a,a[y].a);if(op1==2)swap(a[x].b,a[y].b);if(op1==3)swap(a[x].c,a[y].c);A.upd(1,1,n,a[x].l(),a[x].r()-1,1);A.upd(1,1,n,a[y].l(),a[y].r()-1,1);			}}return 0;
}

CF1554E You

link

冷知识：$\gcd (0,k)=k$。

题目等价于，边 $(u,v)$ 可以选 $u,v$ 中一个贡献 $1$。

观察，发现以下性质：

$k$ 一定 $n-1$ 的因数。因为 $k|a_i$，所以 $k|\sum a_i=n-1$

总方案数是 $2^{n-1}$，证明考虑按照从叶子节点往里删的形式，每一条边选择贡献给叶子或父亲都本质不同。

发现 $k=1$ 不好考虑。

于是先做 $k>1$：

可得，叶子节点连的边一定贡献给父亲，否则叶子节点的 $a$ 为 $1$，则 $\gcd$ 肯定也为 $1$。

那么可以得到一种构造方案——从叶子往中间删边，对于一条边 $(u,v)$ 和叶子 $u$，考虑此时 $a_u$，若不是 $k$ 的倍数，将这条边贡献给 $a_u$，否则贡献给 $a_v$。

这样子最终若是合法，那么就合法。若不合法，你调整也没有用。

且由于删法固定，这样子方案数要么为 $1$，要么为 $0$。

于是我们可以写出代码：

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+1,mod=998244353;
vector<int>E[N];
int n,deg[N],a[N],pw2[N],ans[N],deg1[N];
bool check(int k){queue<int>Q;for(int i=1;i<=n;i++)deg1[i]=deg[i],a[i]=0;for(int i=1;i<=n;i++){if(deg[i]==1)Q.push(i);}while(!Q.empty()){int u=Q.front();Q.pop();for(int v:E[u]){if(!deg1[v])continue;if(a[u]%k!=0)a[u]++;elsea[v]++;deg1[v]--,deg1[u]--;if(deg1[v]==1)Q.push(v);}}for(int i=2;i<=n;i++)a[1]=__gcd(a[1],a[i]);if(a[1]==k)return 1;return 0;
}
void solve(){cin>>n;for(int i=1;i<n;i++){int x,y;cin>>x>>y;E[x].push_back(y),E[y].push_back(x);deg[x]++,deg[y]++;}int o=n-1;for(int i=1;i*i<=o;i++){if(o%i==0)fill(a,a+n+1,0),ans[i]=check(i),ans[o/i]=check(o/i);}ans[1]=pw2[n-1];for(int i=2;i<=n;i++){ans[1]-=ans[i];}ans[1]%=mod,ans[1]+=mod,ans[1]%=mod;for(int i=1;i<=n;i++)cout<<ans[i]<<" ";cout<<"\n";for(int i=1;i<=n;i++)E[i].clear(),deg[i]=0,ans[i]=0,a[i]=0,deg1[i]=0;
}