当前位置：首页 > news >正文

LeetCode 面试经典 150 题：多数元素（摩尔投票法详解 + 多解法对比）

news 2025/9/10 6:20:37

在数组类算法题中，“多数元素” 是一道考察 “高效统计” 思路的经典题目。所谓 “多数元素”，是指在数组中出现次数大于 ⌊n/2⌋（n 为数组长度）的元素，且题目明确说明 “存在唯一的多数元素”。这道题的最优解 ——摩尔投票法，能以 O (n) 时间复杂度和 O (1) 空间复杂度解决问题，是面试中高频考察的 “最优解思路”。本文将从题目解读、摩尔投票法原理、步骤演示，到代码实现，再到其他解法对比，帮你彻底掌握这道题的核心逻辑。

一、题目链接与题干解读

首先，你可以通过以下链接直接访问题目，先自行思考解题方向：

LeetCode 题目链接：169.多数元素

题干核心信息

题目要求如下：

给定一个大小为 n 的数组 nums，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊n/2⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例理解

通过两个典型示例，能更直观理解 “多数元素” 的定义：

示例 1：输入 nums = [3,2,3]，n=3，⌊3/2⌋=1，“3” 出现 2 次（大于 1），因此输出 3；

示例 2：输入 nums = [2,2,1,1,1,2,2]，n=7，⌊7/2⌋=3，“2” 出现 4 次（大于 3），因此输出 2。

二、核心解法：摩尔投票法（Boyer-Moore Voting Algorithm）

摩尔投票法的核心思想是 “多数元素的票数终将盖过其他所有元素的票数之和”。由于多数元素出现次数大于 ⌊n/2⌋，即使其他所有元素联合起来 “对抗” 多数元素，多数元素的 “票数” 也会剩余。这种思路无需统计每个元素的出现次数，仅通过一次遍历即可确定候选多数元素，空间复杂度极低。

1. 摩尔投票法的基本原理

我们可以把整个过程想象成一场 “投票选举”：

每个元素相当于一张 “选票”，投票给对应的 “候选人”（即元素本身）；

我们维护一个 “当前候选人”m和 “当前得票数”cnt：

- 当得票数cnt=0时，说明之前的投票已 “抵消完毕”，需要重新选择新的候选人（即当前遍历到的元素）；

- 当遇到与当前候选人m相同的元素时，得票数cnt加 1（支持当前候选人）；

- 当遇到与当前候选人m不同的元素时，得票数cnt减 1（反对当前候选人，票数抵消）；

由于多数元素的出现次数超过数组长度的一半，最终剩余的 “候选人” 必然是多数元素（题目已保证存在多数元素，无需二次验证）。

2. 核心步骤拆解

摩尔投票法仅需一次遍历，具体步骤如下：

初始化变量：设置 “当前候选人”m（初始值可随意，后续会更新），“当前得票数”cnt = 0；

遍历数组：对于数组中的每个元素x，执行以下判断：

- 若cnt == 0：说明之前的票数已抵消，将当前元素x设为新候选人（m = x），并将得票数初始化为 1（cnt = 1）；

- 若cnt != 0：

- - 若x == m：当前元素支持候选人，得票数加 1（cnt += 1）；

- - 若x != m：当前元素反对候选人，得票数减 1（cnt -= 1）；

返回结果：遍历结束后，m即为多数元素。

3. 示例演示（以示例 2：nums = [2,2,1,1,1,2,2]为例）

我们一步步跟踪m和cnt的变化，直观感受投票过程：

遍历顺序	当前元素x	cnt初始值	判断逻辑	m更新后	cnt更新后	备注
1	2	0	cnt=0 → 设 m=2，cnt=1	2	1	首次选候选人 2
2	2	1	x==m → cnt+1	2	2	支持候选人 2，票数增加
3	1	2	x!=m → cnt-1	2	1	反对候选人 2，票数减少
4	1	1	x!=m → cnt-1	2	0	反对候选人 2，票数抵消为 0
5	1	0	cnt=0 → 设 m=1，cnt=1	1	1	重新选候选人 1
6	2	1	x!=m → cnt-1	1	0	反对候选人 1，票数抵消为 0
7	2	0	cnt=0 → 设 m=2，cnt=1	2	1	重新选候选人 2

遍历结束后，m=2，与示例 2 的正确答案一致。从过程可见，即使中间出现其他候选人（如 1），但由于多数元素 2 的出现次数更多，最终仍会成为剩余的候选人。

三、其他常见解法（对比参考）

除了摩尔投票法，“多数元素” 还有其他解法，虽然复杂度不如摩尔投票法最优，但能帮助我们从不同角度理解问题，以下简要介绍两种：

1. 哈希表统计法（空间复杂度 O (n)）

思路

用哈希表（如 Python 中的字典，Java中的hashMap）记录每个元素的出现次数，遍历数组时更新次数，最后遍历哈希表，返回出现次数大于⌊n/2⌋的元素。

优缺点

优点：逻辑简单直观，易于实现；

缺点：需要额外开辟哈希表空间，空间复杂度为 O (n)，不如摩尔投票法高效。

2. 排序法（时间复杂度 O (n log n)）

思路

由于多数元素出现次数大于⌊n/2⌋，对数组排序后，数组的 “中间位置”（索引为 n//2）的元素必然是多数元素（例如：n=7 时，索引 3；n=3 时，索引 1，均为多数元素）。

优缺点

优点：代码极简，依赖排序 API 即可实现；

缺点：排序的时间复杂度为 O (n log n)，不如摩尔投票法的 O (n) 高效。

代码片段（Python）

class Solution:def majorityElement(self, nums: List[int]) -> int:nums.sort()return nums[len(nums) // 2]

四、复杂度分析（摩尔投票法）

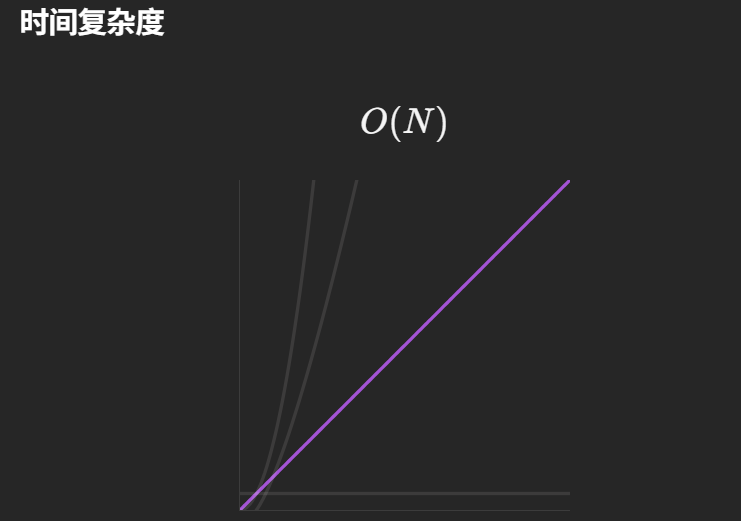
1. 时间复杂度：O (n)

摩尔投票法仅对数组进行一次遍历，每个元素只参与一次 “判断 - 更新” 操作，无嵌套循环；

遍历次数与数组长度 n 成正比，因此时间复杂度为线性的 O (n)。

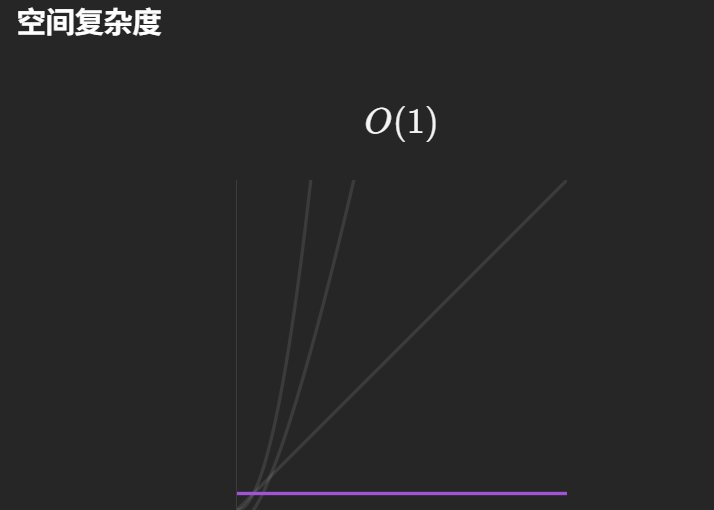
2. 空间复杂度：O (1)

整个过程只用到了两个额外变量（m和cnt），没有开辟新的数组、哈希表或其他数据结构；

额外空间的使用与数组长度 n 无关，因此空间复杂度为常数级的 O (1)。

五、摩尔投票法代码实现

以下以 Python ，Java为例，实现摩尔投票法：

1，Python

class Solution:def majorityElement(self, nums: List[int]) -> int:cnt = 0m = 0for x in nums:if cnt == 0:m = xcnt = 1else:cnt += 1 if m == x else -1return m

2，Java

class Solution {public int majorityElement(int[] nums) {int cnt = 0, m = 0;for (int x : nums) {if (cnt == 0) {m = x;cnt = 1;} else {cnt += m == x ? 1 : -1;}}return m;}
}

你可以将上述代码复制到 LeetCode 编辑器中测试，完全符合题目要求。