机器学习回顾(二)——KNN算法

什么是KNN算法？

全称是k-nearest neighbors，通过寻找k个距离最近的数据，来确定当前数据值的大小或类别。是机器学习中最为简单和经典的一个算法。

假设你有一个数据集，其中每个数据点都有若干个特征，并且已知它的类别（如果是分类问题）或者数值（如果是回归问题）。

当来了一个​​新的未知样本​​，KNN算法会这样做：

1. ​​计算新样本与数据集中所有样本的距离​​（比如欧几里得距离）；
2. 选出距离最近的 K 个样本​​（K 是你自己设定的一个正整数，比如 K=3、K=5）；
3. 根据这 K 个邻居的信息进行预测​​：
   • ​​如果是分类问题​​：采用​​投票制​​，哪个类别的邻居最多，新样本就属于哪个类别；
   • 如果是回归问题​​：采用​​平均值​​，取这 K 个邻居输出值的平均作为预测值。

假设我们有以下二维平面上的几个点（2个类别：红色○ 和 蓝色×）：

红色○：(1, 2), (2, 3), (3, 1) 蓝色×：(6, 5), (7, 7), (8, 6) 现在有一个新点：(5, 4)，我们想知道它属于红色还是蓝色。

如果我们设定 ​​K=3​​，那么：

1. 计算 (5,4) 与所有点的距离；
2. 找出距离最近的 3 个点；
3. 看这 3 个点中哪种颜色（类别）多，新点就归为哪一类。

 这就是KNN的直观思想：​​近朱者赤，近墨者黑​​。

---

KNN算法关键点解析

1. ​​距离度量（Distance Metric）​​

KNN需要计算样本之间的距离，常见的距离公式有：

• 欧几里得距离（Euclidean Distance）​​：最常用

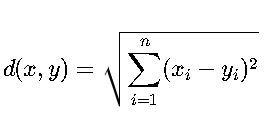
即两点在各维度上的差值平方和再开根号。

• ​​曼哈顿距离（Manhattan Distance）​​

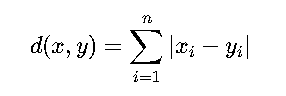
• 余弦相似度（Cosine Similarity）​​：适用于文本等方向性数据

你可以根据问题选择不同的距离计算方式。

---

2. ​​K值的选择（最重要的超参数）​​

• ​​K 值太小（如 K=1）​​：模型对噪声敏感，容易过拟合（受到个别异常点影响大）；
• ​​K 值太大​​：模型过于平滑，可能把不同类别的点也考虑进来，导致欠拟合；
• ​​通常通过交叉验证来选择最优的 K 值​​，常见尝试范围是 3、5、7、9 等​​奇数​​（避免平票）。

---

3. ​​分类 or 回归？​​

• ​​分类任务​​：K个邻居里哪个类别最多，新样本就属于该类（多数表决）；
• 回归任务​​：K个邻居的输出值的平均值，作为预测值。

---

KNN算法的优点与缺点

优点：

• ​​思想简单，易于理解与实现​​
• 无需训练过程（惰性学习 Lazy Learning）​​：模型只是保存数据，预测时才进行计算
• 对数据分布没有假设​​，适用于多种类型的数据
• 对于小规模数据表现良好

缺点：

• 计算量大（预测时需要计算与所有样本的距离）​​，不适合大数据集
• ​​对高维数据效果变差（维度灾难）​​
• 对异常值敏感​​
• 需要合理选择 K 值和距离度量方式​​

---

KNN算法的应用场景

• ​​手写数字识别​​（如MNIST数据集分类）
• ​​推荐系统​​（找相似用户/物品）
• 图像识别​​（简单场景）
• 异常检测​​
• 医疗诊断​​（根据病人特征匹配相似病例）

示例

from matplotlib import pyplot as plt
import numpy as np
'''KNN（K-Nearest Neighbors）算法是一种简单而有效的监督学习方法，主要用于分类和回归任务。
它的核心思想是：相似的数据点在特征空间中通常属于同一类别或具有相似的值。'''
'''寻找k个距离最近的数据，k根据项目的数据量决定'''
'''欧式距离，点到点的距离'''
'''曼哈顿距离'''
'''sklearn.neighbors.KNeighborsClassifier(
n_neighbors=5,k值
weights='distance',
algorithm='auto',
leaf_size=30,
metric='minkowski',
metric_params=None,
n_jobs=1,
p=2)'''# data = np.loadtxt('datingTestSet2.txt', delimiter='\t')#numpy读取文件
# study1 = data[data[:,-1] == 1]#分类，提取。
# study2 = data[data[:,-1] == 2]
# study3 = data[data[:,-1] == 3]
#
#
# #可视化
# fig = plt.figure()   #创建图像
# ax = plt.axes(projection='3d') #建立三维图像
# ax.scatter(study1[:,0], study1[:,1], study1[:,2], c='#FF0000',marker='X') #导入数据
# ax.scatter(study2[:,0], study2[:,1], study2[:,2], c='#0000FF',marker='^')
# ax.scatter(study3[:,0], study3[:,1], study3[:,2], c='#008000',marker='D')
# ax.set(xlabel='x', ylabel='y', zlabel='z')#设置x,y,z轴名称
# plt.title('散点图')
# plt.legend(['study1', 'study2', 'study3'])#添加图例
# plt.show()#knn算法预测
from sklearn.neighbors import KNeighborsClassifier
data = np.loadtxt('datingTestSet2.txt', delimiter='\t')
neigh = KNeighborsClassifier(n_neighbors=5)
x=data[:800,:-1]
y=data[:800,-1]
neigh.fit(x,y)
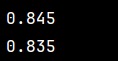
print(neigh.score(x,y))#准确率,自测
c1=data[800:,:-1]
c2=data[800:,-1]
right=neigh.score(c1,c2)
print(right)
# print(neigh.predict([[44440,4,0.9]]))#预测数据，接受二维数据# predict_data = np.loadtxt('predict_data.txt', delimiter='\t')
# print(neigh.predict(predict_data))
'''
TP:真正例
TN:真反例
FP:假正例
FN:假反例
准确率（Accuracy） =(TP + TN)/
(TP+TN+FP+FN)
正确预测的比例，适用于类别平衡数据
精确率（Precision）=TP/
(TP+FP)
预测为正的样本中实际为正的比例
召回率（Recall）= TP/
(TP+FN)
实际为正的样本中被正确预测的比例
F1分数（F1-Score） =
2×Precision×Recall/
(Precision+Recall)
精确率和召回率的调和平均，适用于不平衡数据
'''