SciPy科学计算与应用：SciPy入门与应用-科学计算与NumPy协同实践

SciPy实践：从基础到应用

学习目标

通过本课程的学习，学员将掌握SciPy库的基本使用方法，了解其在科学计算中的应用，以及如何与NumPy库协同工作，解决实际问题。

相关知识点

SciPy实践

学习内容

1 SciPy实践

1.1 SciPy库概述

SciPy是一个基于Python的开源软件，用于科学和工程计算。它建立在NumPy之上，提供了大量的数学算法和方便的数据处理功能。SciPy库的设计目的是为了提供一个高效、易于使用的工具集，用于解决科学、工程和数学问题。它包含了用于优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理等领域的子模块。

SciPy的历史可以追溯到2001年，由Travis Oliphant等人开发。随着时间的发展，SciPy已经成为Python科学计算生态系统中的核心组件之一。它不仅在学术界广泛使用，也被工业界所接受，成为数据科学家、工程师和研究人员的首选工具之一。

1.2 SciPy与NumPy的关系

NumPy和SciPy是Python科学计算中两个非常重要的库，它们之间有着密切的关系。NumPy主要提供了一个强大的N维数组对象，以及用于处理这些数组的工具，如数学函数、线性代数操作、傅里叶变换等。而SciPy则是在NumPy的基础上，提供了更多的科学计算功能，如优化、统计、信号处理等。

NumPy可以看作是SciPy的基础，SciPy中的许多功能都依赖于NumPy的数组对象。例如，当学员使用SciPy进行线性代数计算时，实际上是在使用NumPy提供的数组来存储数据。因此，学习SciPy之前，了解NumPy的基本操作是非常有帮助的。

1.3 SciPy在科学计算中的应用实例

为了更好地理解SciPy在实际中的应用，我们将通过几个具体的例子来展示如何使用SciPy解决科学计算问题。

1.3.1 积分计算

积分是数学中的一个基本概念，广泛应用于物理、工程等领域。SciPy提供了scipy.integrate模块，用于数值积分。下面是一个使用SciPy计算定积分的例子：

from scipy.integrate import quad
import numpy as np# 定义被积函数
def integrand(x):return np.exp(-x**2)# 计算定积分
result, error = quad(integrand, 0, np.inf)
print(f"积分结果: {result}, 估计误差: {error}")

积分结果: 0.8862269254527579, 估计误差: 7.101318529726462e-09

在这个例子中，我们定义了一个被积函数integrand，然后使用quad函数计算了从0到正无穷的定积分。quad函数返回两个值：积分结果和估计误差。

1.3.2 优化问题

优化是科学计算中的另一个重要领域，SciPy提供了scipy.optimize模块，用于解决各种优化问题。下面是一个使用SciPy进行最小化优化的例子：

from scipy.optimize import minimize
import numpy as np# 定义目标函数
def objective(x):return x[0]**2 + x[1]**2# 初始猜测值
x0 = [1, 1]# 进行最小化优化
result = minimize(objective, x0, method='BFGS')
print(f"最小值: {result.fun}, 最优解: {result.x}")

最小值: 2.311471135620994e-16, 最优解: [-1.07505143e-08 -1.07505143e-08]

在这个例子中，我们定义了一个目标函数objective，然后使用minimize函数进行最小化优化。minimize函数返回一个结果对象，其中包含了最小值和最优解。

1.3.3 信号处理
信号处理是另一个重要的应用领域，SciPy提供了scipy.signal模块，用于处理各种信号。下面是一个使用SciPy进行信号滤波的例子：

from scipy.signal import butter, lfilter
import numpy as np
import matplotlib.pyplot as plt# 定义巴特沃斯滤波器
def butter_lowpass(cutoff, fs, order=5):nyq = 0.5 * fsnormal_cutoff = cutoff / nyqb, a = butter(order, normal_cutoff, btype='low', analog=False)return b, adef butter_lowpass_filter(data, cutoff, fs, order=5):b, a = butter_lowpass(cutoff, fs, order=order)y = lfilter(b, a, data)return y# 生成测试信号
fs = 500.0  # 采样频率
T = 5.0     # 信号持续时间
n = int(T * fs)  # 总采样点数
t = np.linspace(0, T, n, endpoint=False)
data = np.sin(1.2 * 2 * np.pi * t) + 1.5 * np.cos(9 * 2 * np.pi * t) + 0.5 * np.sin(12.0 * 2 * np.pi * t)# 应用低通滤波器
cutoff = 3.667  # 截止频率
y = butter_lowpass_filter(data, cutoff, fs, order=6)# 绘制结果
plt.figure()
plt.plot(t, data, label='raw signal')
plt.plot(t, y, label='filtered signal')
plt.legend()
plt.show()

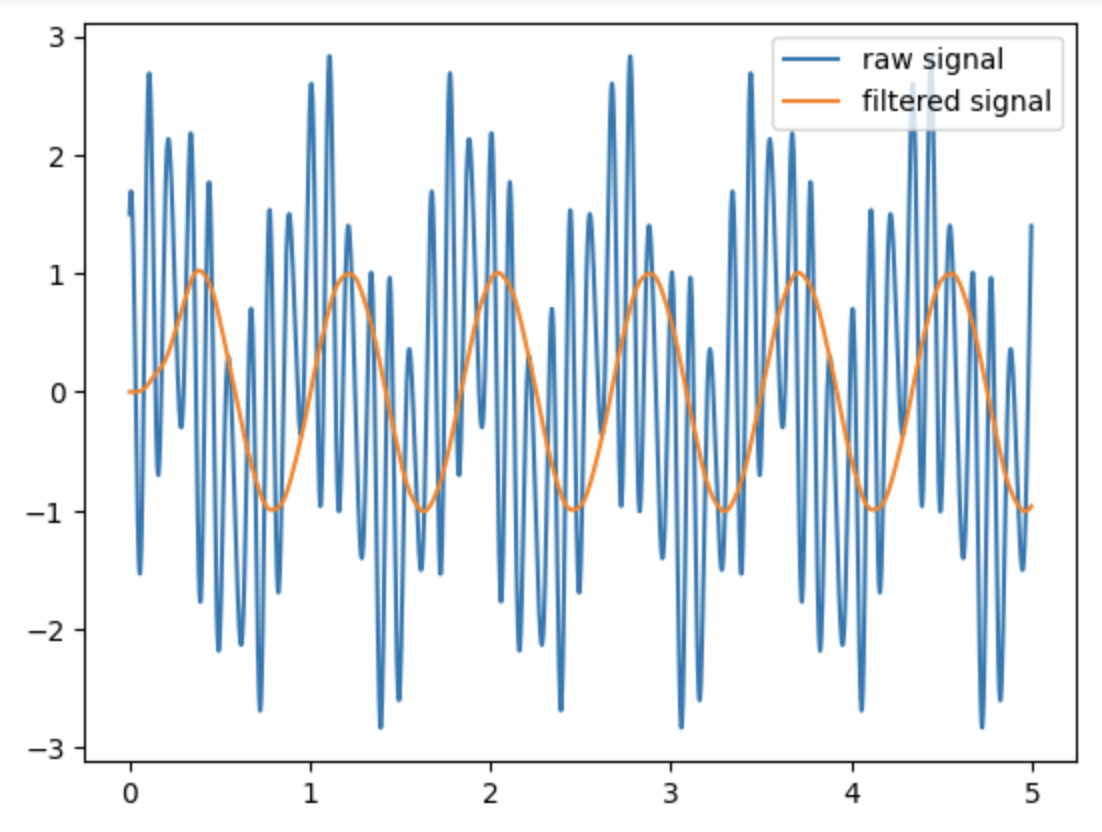
在这个例子中，我们定义了一个巴特沃斯低通滤波器，并使用lfilter函数对信号进行滤波。最后，我们使用Matplotlib绘制了原始信号和滤波后的信号，以便直观地观察滤波效果。