【机器学习基础】朴素贝叶斯算法详解：从原理到实战

一、贝叶斯方法简介

贝叶斯方法源于18世纪英国数学家托马斯·贝叶斯（Thomas Bayes）提出的“逆概率”问题。其核心思想是通过观测数据来更新对某个假设的信念。

正向概率 vs 逆向概率：

正向概率：已知模型参数，求观测数据的概率。

逆向概率：已知观测数据，推断模型参数或隐藏状态。

贝叶斯公式：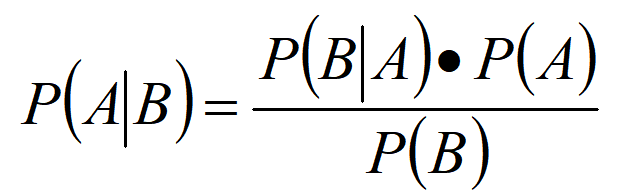

其中：

P(A|B) 是后验概率，P(A)是先验概率，P(B|A)是似然概率，P(B)是证据因子。

二、朴素贝叶斯算法

朴素贝叶斯是一种基于贝叶斯定理的分类算法，其“朴素”在于假设所有特征之间相互独立。

1. 拼写纠正：

用户输入一个词 D，我们想找出最可能的正确词 h：

𝑃(ℎ∣𝐷)∝𝑃(ℎ)⋅𝑃(𝐷∣ℎ)P(h∣D)∝P(h)⋅P(D∣h)

P(h)：词 h 出现的先验概率（如语料库中的频率）

P(D|h)：正确词为 h时输入为 $D$ 的概率（如编辑距离）

2. 垃圾邮件分类：

将邮件 D分为垃圾邮件（h+）或正常邮件（h-）：

𝑃(ℎ+∣𝐷)=𝑃(ℎ+)⋅𝑃(𝐷∣ℎ+)𝑃(𝐷)P(h+∣D)=P(D)P(h+)⋅P(D∣h+)​

在朴素假设下：

𝑃(𝐷∣ℎ+)=𝑃(𝑑1∣ℎ+)⋅𝑃(𝑑2∣ℎ+)⋅…⋅𝑃(𝑑𝑛∣ℎ+)P(D∣h+)=P(d1​∣h+)⋅P(d2​∣h+)⋅…⋅P(dn​∣h+)

三、三种常见的朴素贝叶斯变体

1. 多项式朴素贝叶斯（MultinomialNB）：

适用场景：离散特征，如文本分类（词频统计）

实现方式：from sklearn.naive_bayes import MultinomialNB

2. 高斯朴素贝叶斯（GaussianNB）：

适用场景：连续特征，符合正态分布

实现方式：from sklearn.naive_bayes import GaussianNB

3. 伯努利朴素贝叶斯（BernoulliNB）：

适用场景：二值离散特征（0/1，出现/未出现）

实现方式：from sklearn.naive_bayes import BernoulliNB

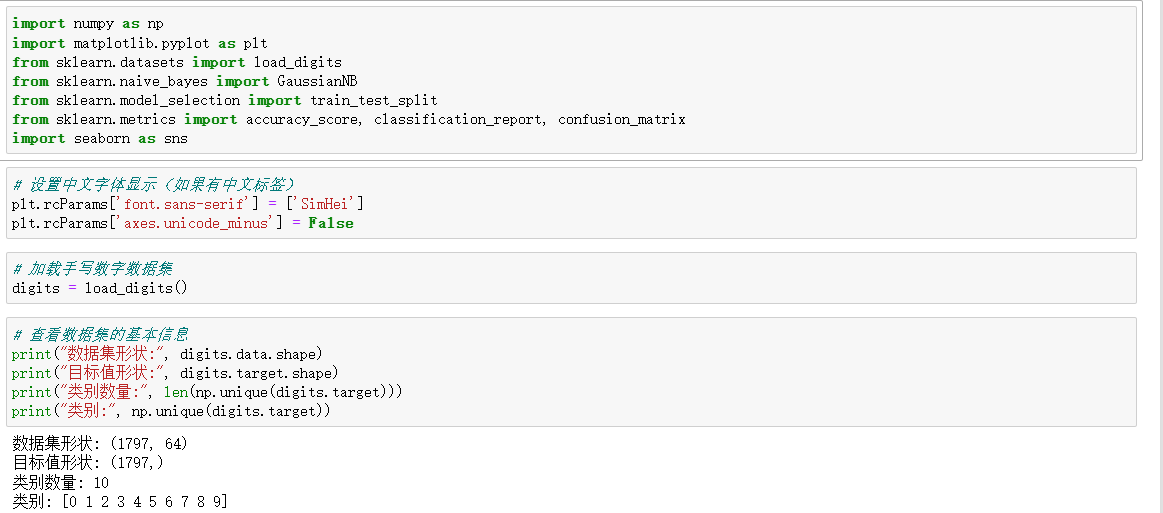
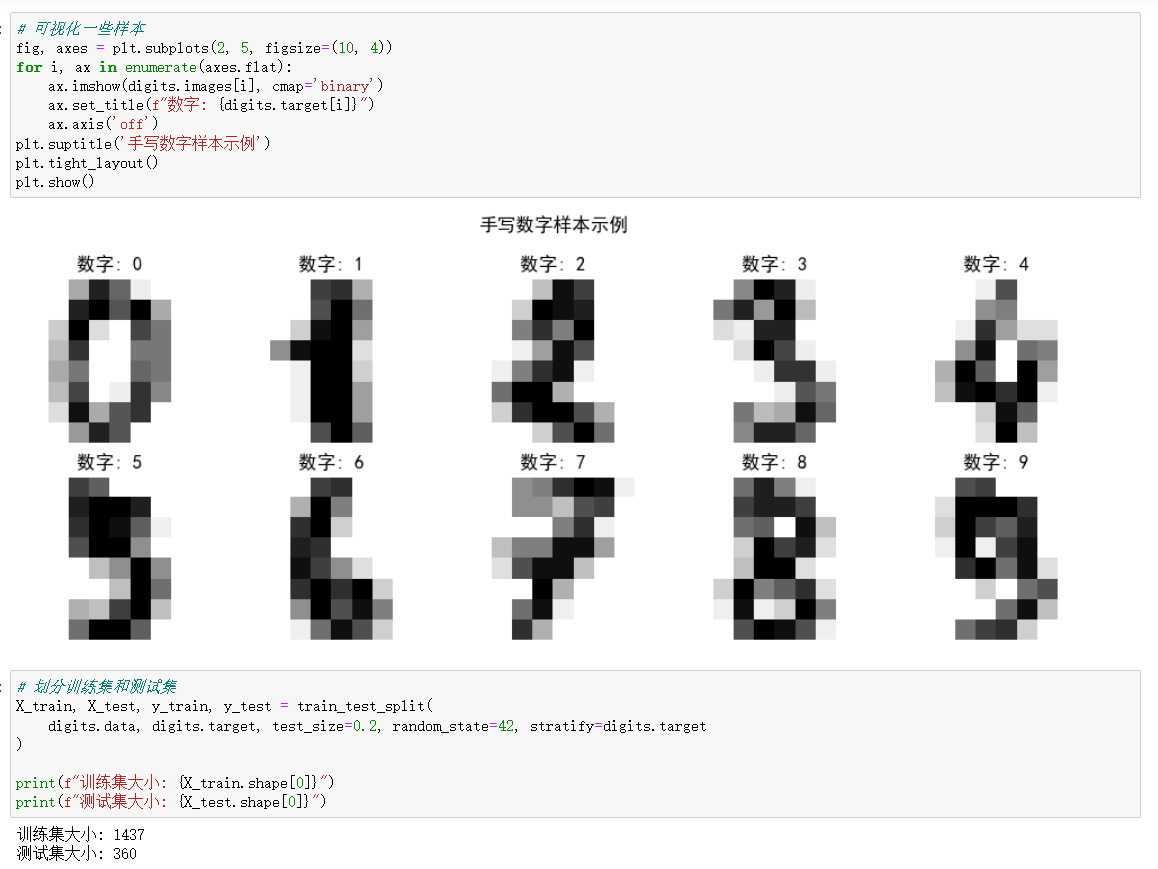
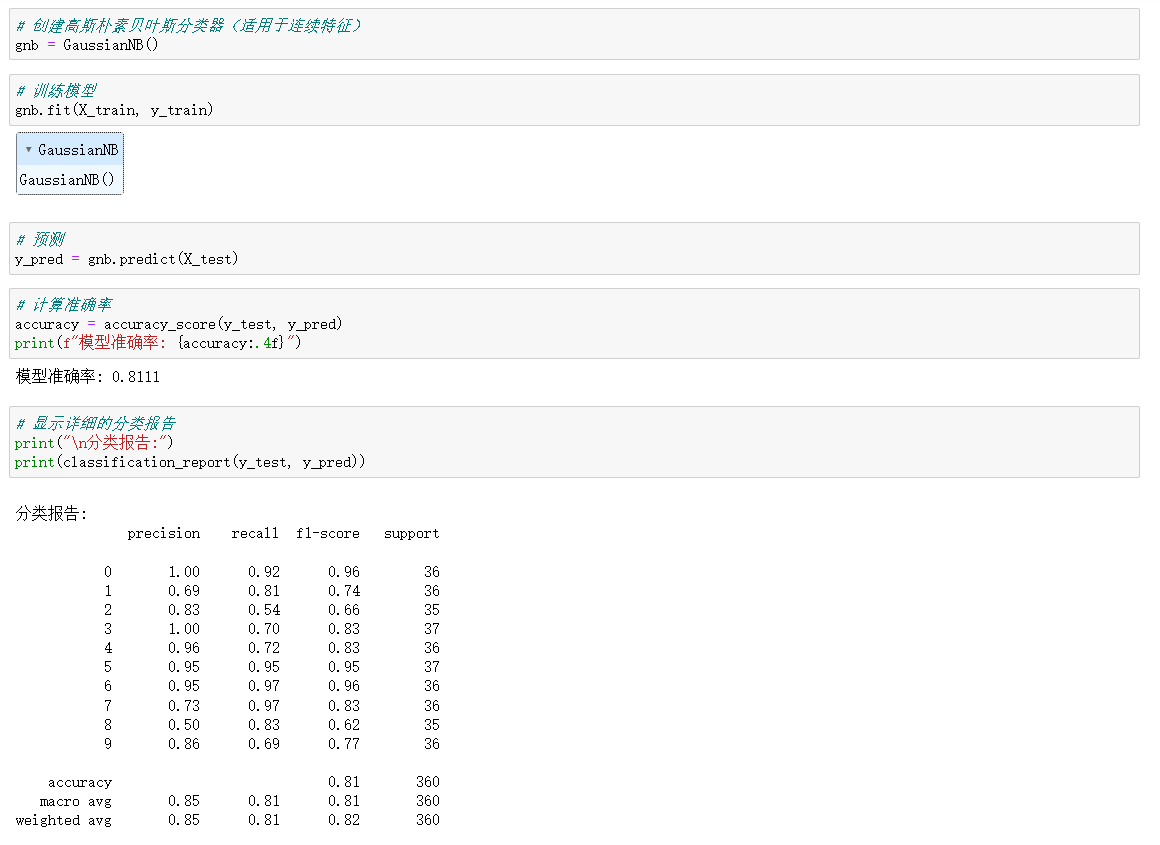
四、实战示例：手写数字识别

使用 sklearn 中的手写数字数据集进行朴素贝叶斯分类：

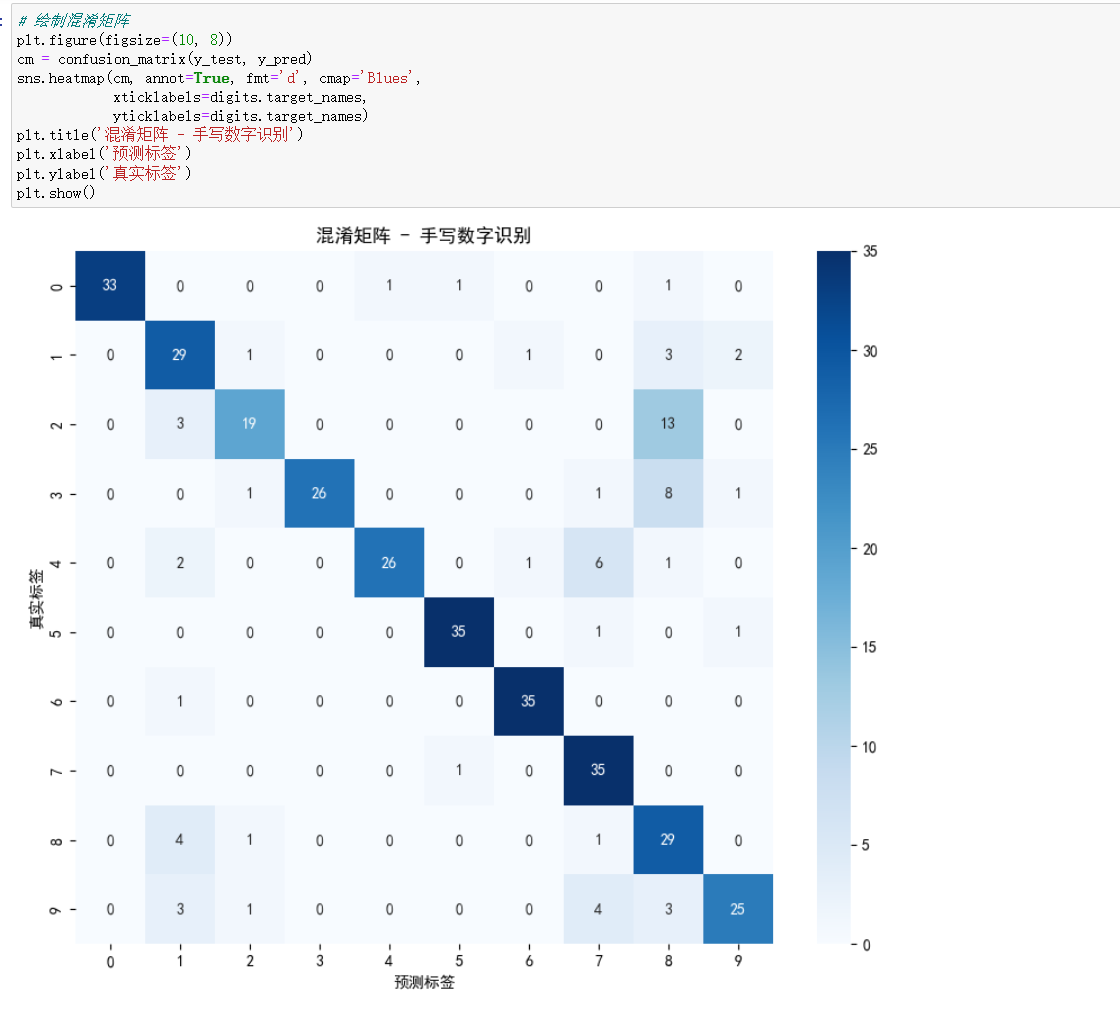
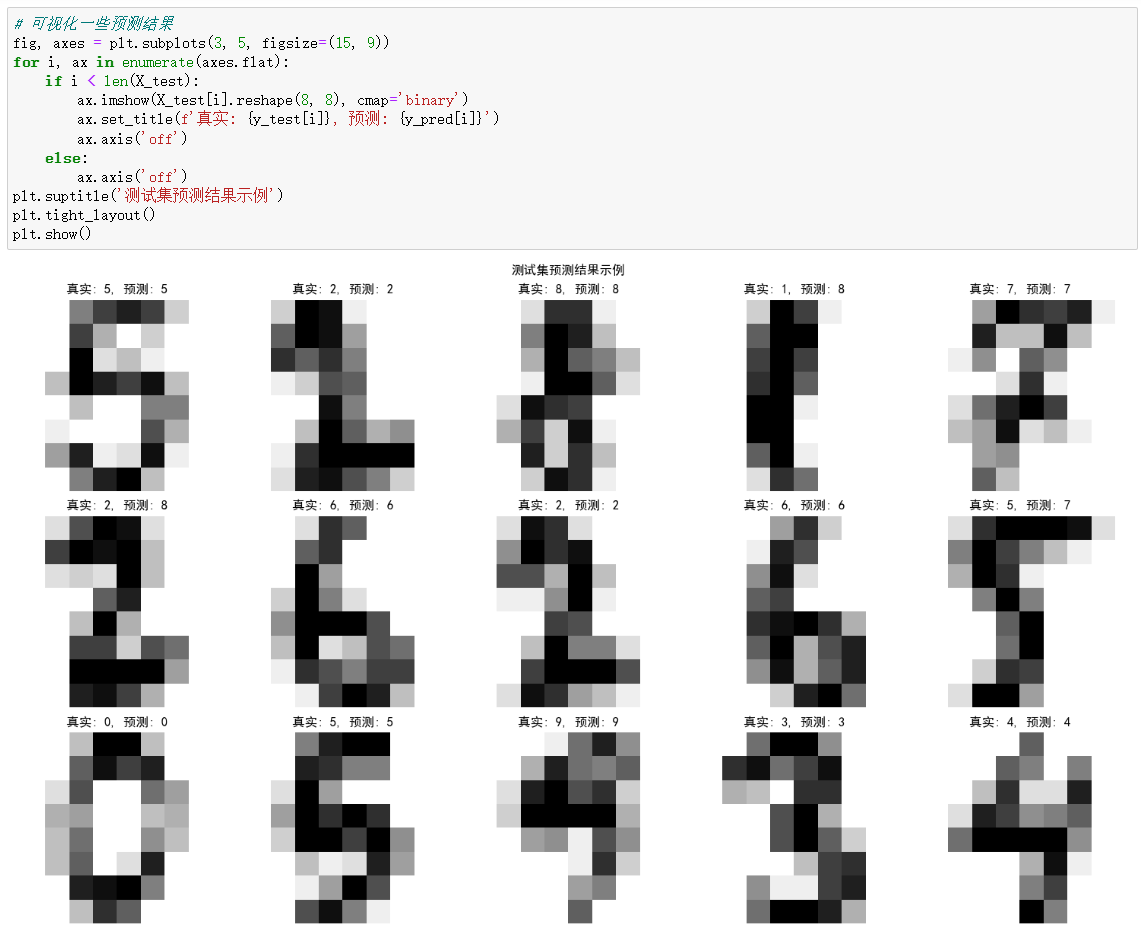
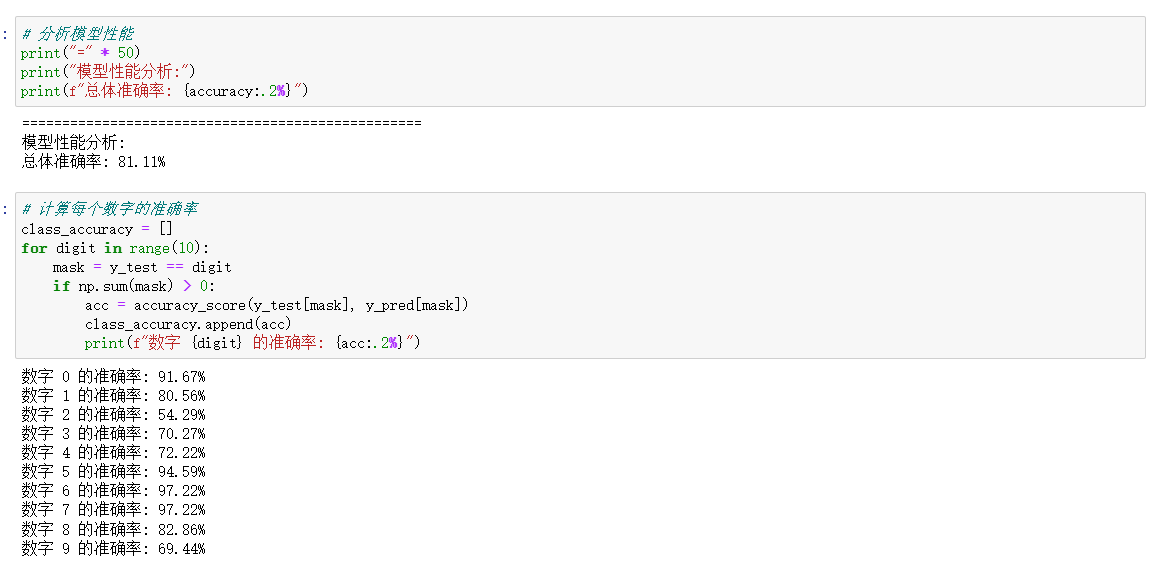
五、总结

朴素贝叶斯是一种简单高效、适合高维数据的分类算法。

其“条件独立”假设在现实中往往不成立，但在文本分类等领域表现优异。

根据特征类型选择不同的贝叶斯变体（多项式、高斯、伯努利）是关键。