文献阅读笔记：KalmanNet-融合神经网络和卡尔曼滤波的部分已知动力学状态估计

摘要

实时估计动态系统的隐藏状态是信号处理、控制和导航等领域的核心任务。卡尔曼滤波（KF）及其非线性变体（如扩展卡尔曼滤波EKF、无迹卡尔曼滤波UKF）在处理线性高斯状态空间（SS）模型时具有理论最优性和计算高效性。然而，实际系统往往具有非线性动态特性，且模型参数（尤其是噪声统计特性）难以精确获知，导致基于模型（MB）的滤波方法性能显著下降。另一方面，纯粹数据驱动（DD）的深度神经网络（DNN），特别是循环神经网络（RNN），虽能学习复杂动态，但通常需要大量数据和参数，缺乏可解释性，且难以融入已知的领域知识。

本文精读的论文《KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics》提出了一种名为KalmanNet的混合MB/DD实时状态估计器，旨在解决部分已知非线性动态系统的状态估计问题。KalmanNet的核心思想是保留经典卡尔曼滤波（特别是EKF）的递归结构和已知的SS模型部分（状态转移函数$f(\cdot )$和观测函数$h(\cdot )$），同时利用一个紧凑的RNN模块来学习并替代传统卡尔曼滤波中依赖于噪声统计模型的关键计算环节——卡尔曼增益（KG）。这种方法结合了MB方法的可解释性、数据效率和DD方法处理模型失配与非线性的能力。

论文详细阐述了KalmanNet的高层架构、输入特征设计、两种具体的RNN实现架构（隐式联合跟踪和显式分离跟踪二阶统计矩）以及高效的监督训练方案（包括通过时间反向传播BPTT的变体）。通过大量的数值实验，论文在多种场景下验证了KalmanNet的有效性：

1. 线性SS模型中，KalmanNet在完全信息下达到与MBKF相同的最小均方误差（MMSE），在模型失配情况下显著优于MBKF；
2. 合成非线性模型（正弦和多项式）中，KalmanNet克服了EKF、UKF和粒子滤波（PF）在处理严重非线性和模型失配时的性能下降；
3. 混沌Lorenz吸引子模型中，KalmanNet在处理状态转移近似误差、观测旋转失配和连续-离散采样失配时展现出强大的鲁棒性；
4. 基于真实世界密歇根NCLT数据集的定位任务中，KalmanNet显著优于基于线性运动模型的MBKF和纯DD的RNN估计器，有效克服了里程计漂移问题。

实验结果表明，KalmanNet在保持接近传统MB滤波计算复杂度的同时，能够有效处理非线性和模型不确定性，性能优于现有主流MB和DD方法，且学习结果具有良好的可迁移性（训练短轨迹应用于长轨迹）。KalmanNet为在硬件资源受限设备（如无人机、车辆系统）上实现高性能实时状态估计提供了新思路，并具有良好的可扩展性。

一、研究背景

在阅读论文《KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics》之后，在了解了研究的背景的同时，我也发现其结构非常符合信号处理领域的论文写作框架，这对我今后的论文写作具有重要意义。例如，该论文的引言部分可划分为如下四个部分，主要包括问题研究意义的介绍、传统方法的局限性、问题解决思路、创新性及论文结构，下面逐一进行介绍。

1.1 状态估计问题的重要性

实时估计动态系统的隐藏状态是信号处理、自动控制、导航、跟踪、机器人学等领域的基石任务。无论是跟踪飞行器轨迹、估计车辆位置速度、预测金融市场变化，还是从生物信号中提取特征，其核心问题都是如何从带有噪声的观测序列中，在线地、递归地推断出无法直接测量的系统内部状态。卡尔曼滤波（Kalman Filter，KF）自20世纪60年代被提出以来，因其在线性高斯状态空间（State Space，SS）模型下具有最小均方误差的最优性以及计算高效的递归结构，已成为解决此类问题的标杆算法，并在阿波罗计划等重大工程中得到成功应用。

1.2 传统方法的局限：非线性与模型不确定性

然而，现实世界中的动态系统往往表现出非线性行为，且精确的SS模型参数（特别是过程噪声协方差矩阵$Q$和观测噪声协方差矩阵$R$）通常难以完全获知或精确建模。这给传统KF及其扩展带来了严峻挑战：

非线性问题

经典KF仅适用于线性系统。针对非线性系统，研究者提出了扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）、容积卡尔曼滤波（CKF）以及基于序贯蒙特卡洛（MC）采样的粒子滤波（PF）。EKF通过对非线性函数进行一阶泰勒展开（雅可比矩阵）实现局部线性化，UKF/CKF则采用确定性采样点逼近状态分布。PF通过一组带有权重的粒子来近似状态的后验概率密度函数（PDF），理论上能处理任意非线性和非高斯噪声，但计算复杂度高。这些方法的共同点是：

• 模型依赖性强：性能严重依赖于对非线性函数（状态转移）和（观测）以及噪声统计特性的精确已知。
• 模型失配敏感：当使用的模型参数与真实系统存在偏差（模型失配）时，性能会显著下降。EKF的线性近似在强非线性或模型不准时容易发散或精度降低；UKF/CKF对模型参数同样敏感；PF虽对非线性鲁棒，但对模型参数失配和粒子退化问题敏感。
• 鲁棒方法代价高：鲁棒KF变体或鲁棒PF通过优化最坏情况性能来处理模型不确定性，但这通常以牺牲在精确模型下的最优性能为代价。

噪声统计未知问题

即使系统是线性的，若噪声协方差未知，传统KF也无法直接应用。参数估计方法（如期望最大化算法）或在线调参存在计算复杂、依赖参数化模型假设（如高斯噪声）等限制。

1.3 数据驱动方法的兴起与局限

近年来，深度神经网络（DNN），特别是循环神经网络（RNN）如LSTM、GRU，在处理序列数据（如时间序列预测、语音识别）方面展现出强大的能力。这为状态估计提供了一条替代路径：直接从数据中学习状态估计的映射关系，无需显式指定SS模型。纯粹DD方法的主要优势在于其模型无关性，能够隐式捕捉复杂和非线性的动态关系。然而，它们也存在明显缺点：

• 数据饥渴：通常需要大量的标记数据和众多的可训练参数，即使对于相对简单的动态序列。
• 缺乏可解释性：作为“黑盒”模型，其内部决策过程和估计结果的可信度难以解释，在安全关键应用中受限。
• 难以融入领域知识：没有系统性的方法将已知的物理模型或结构化知识有效地整合到网络中。
• 计算开销：大型RNN的推理复杂度可能较高，在嵌入式或实时性要求高的场景（如无人机、车载系统）部署困难。

1.4 KalmanNet：混合方法的创新

基于上述MB和DD方法的局限性，一个自然的思路是寻求两者的结合，取长补短。本报告精读的论文《KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics》正是这一方向的代表性工作。论文的核心贡献在于提出了KalmanNet——一种新颖的、可解释的、数据高效的混合MB/DD实时状态估计器。

KalmanNet的核心创新点在于：

1. 保留MB骨架：它继承了经典卡尔曼滤波（特别是EKF）的递归计算流程（预测-更新）和理论框架，并充分利用了部分已知的领域知识（即状态转移函数和观测函数，即使它们可能是近似或不精确的）。
2. DD学习关键环节：它识别出传统KF/EKF中最依赖于精确噪声统计模型的计算环节——卡尔曼增益（Kalman Gain，KG）的计算（涉及矩阵求逆和二阶矩传播）。
3. RNN替代KG计算：它用一个专门设计的、复杂度可控的循环神经网络（RNN）模块替代了传统的、基于模型公式的KG计算。该RNN接收一组精心设计的输入特征（包含观测和状态估计的差异信息），输出当前时刻的KG矩阵。
4. 监督学习与高效训练：KalmanNet利用带标签的数据集（观测序列和对应真实状态序列）以监督学习的方式端到端进行训练，损失函数直接作用于状态估计误差。论文提出了有效的训练策略（包括截断BPTT）使其能够处理任意长轨迹，而仅需使用短轨迹进行训练。

这种混合架构旨在同时获得：

• MB方法的优势：数据效率高、可解释性强（保持了KF的流程和中间变量的物理意义）、计算复杂度相对较低（避免了纯DD大网络）。
• DD方法的优势：能够从数据中学习如何处理模型失配和非线性，无需精确的噪声统计模型，绕过数值不稳定的矩阵求逆。

1.5 本文精读内容与结构

本读书报告旨在对KalmanNet这篇论文进行深入精读和分析，报告将围绕论文的核心内容展开：

• 第2部分：梳理相关的工作，包括状态空间模型、卡尔曼滤波（EKF）原理，并对比与KalmanNet相关的其他融合深度学习和状态空间模型的工作。
• 第3部分：KalmanNet技术路线解析是本报告的核心，将详细阐述KalmanNet的架构设计理念、输入特征选择、两种具体的RNN实现方案以及训练算法细节，并进行深入的讨论分析其优势与设计考量。
• 第4部分：实验与结果分析将系统梳理论文中进行的广泛数值实验（线性模型、合成非线性模型、Lorenz吸引子、NCLT真实数据集），分析KalmanNet在各种场景（完全信息、部分信息/模型失配、非线性、真实数据）下的性能表现，并与多种基线方法（KF,EKF,UKF,PF,纯RNN）进行对比。
• 第5部分：总结与思考将总结KalmanNet的主要贡献、优势和适用场景，讨论其局限性，并展望未来可能的扩展方向。同时结合自身理解，探讨该工作对现代信号处理中状态估计研究的启示和实际应用潜力。

通过这份精读报告，我们将深入理解KalmanNet的工作原理、技术细节、性能优势及其在现代信号处理，特别是在非线性滤波和模型不确定性问题处理中的重要价值。

二、相关工作及问题描述

为了深入理解KalmanNet的创新点和贡献，本节将系统回顾状态空间模型、经典卡尔曼滤波（特别是扩展卡尔曼滤波EKF）的原理，并分析与KalmanNet相关的其他融合深度学习和状态空间模型的研究工作，明确KalmanNet在相关研究领域中的定位和独特之处。

2.1 状态空间模型(State Space Model)

动态系统通常使用离散时间状态空间模型来描述：
$$x_k=f(x_{k-1},w_{k-1}),y_k=h(x_k,v_k)\text{\hspace{1em}(1)}$$
其中，

• $x_k$：$k$时刻系统的$m$维隐藏状态向量（如位置、速度、温度等），
• $f(\cdot )$：（可能非线性的）状态转移函数，描述状态如何从$k-1$时刻演化到$k$时刻，
• $w_{k-1}$：过程噪声（通常假设为加性高斯白噪声，AWGN），协方差矩阵为$Q$，
• $y_k$：$k$时刻的$n$维观测向量，
• $h(\cdot )$：（可能非线性的）观测函数，描述状态如何映射到观测，
• $v_k$：观测噪声（通常假设为加性高斯白噪声，AWGN），协方差矩阵为$R$。

当$f(x_{k-1},w_{k-1})=F{x}_{k-1}+w_{k-1}$和$h(x_k,v_k)=H{x}_k+v_k$时，模型退化为线性高斯状态空间模型。

状态空间模型支持多种任务：

• 滤波(Filtering)：本论文核心任务。在线地估计当前时刻$k$的状态$x_k$，仅基于当前和过去的所有观测$y_{1:k}$。输出是${\hat{x}}_{k|k}$。
• 平滑(Smoothing)：离线地估计过去某个时刻$k$的状态$x_k$，基于整个观测序列$y_{1:T}$（$k<T$）。输出是${\hat{x}}_{k|T}$。
• 预测(Prediction)：预测未来时刻$k>t$的状态$x_k$或观测$y_k$，基于当前和过去的观测$y_{1:t}$。
• 观测近似：如插值（Imputation）、去噪（Denoising）。

2.2 卡尔曼滤波(KF)与扩展卡尔曼滤波(EKF)

2.2.1 线性卡尔曼滤波(KF)

对于线性高斯SS模型($f=Fx+w,h=Hx+v$)，卡尔曼滤波提供了一种递归的、最优的（MMSE）状态估计方法。其核心是预测-更新两步骤：

1. 预测(Prediction)：
   $${\hat{x}}_{k|k-1}=F{\hat{x}}_{k-1|k-1},P_{k|k-1}=F{P}_{k-1|k-1}{F}^T+Q,{\hat{y}}_{k|k-1}=H{\hat{x}}_{k|k-1},S_k=H{P}_{k|k-1}{H}^T+R\text{\hspace{1em}(2)}$$
   利用状态转移矩阵$F$预测当前状态的先验估计${\hat{x}}_{k|k-1}$和先验误差协方差$P_{k|k-1}$；预测当前观测${\hat{y}}_{k|k-1}$及其协方差$S_k$。

2. 更新(Update)：
   $${\tilde{y}}_k=y_k-{\hat{y}}_{k|k-1},K_k=P_{k|k-1}{H}^T{S}_k^{-1},{\hat{x}}_{k|k}={\hat{x}}_{k|k-1}+K_k{\tilde{y}}_k,P_{k|k}=P_{k|k-1}-K_k{S}_k{K}_k^T\text{\hspace{1em}(3)}$$
   计算新息（Innovation）${\tilde{y}}_k$，即观测预测值与实际观测值的差；计算卡尔曼增益$K_k$。它权衡了预测的不确定性（先验协方差$P_{k|k-1}$）和观测的不确定性（观测噪声协方差$R$，通过$S_k$体现）。$K_k$依赖于$Q$和$R$（通过$P_{k|k-1}$和$S_k$），并涉及矩阵求逆($S_k^{-1}$)。接着，利用卡尔曼增益和新息更新状态的后验估计${\hat{x}}_{k|k}$和后验误差协方差$P_{k|k}$。

KF是递归的，计算复杂度不随时间增长，且在线性高斯假设下是MMSE最优的。但其性能极度依赖于线性模型($F,H$)和噪声统计($Q,R$)的精确已知。

2.2.2 扩展卡尔曼滤波(EKF)

当状态转移$f(\cdot )$或观测函数$h(\cdot )$为非线性时，EKF是最常用的扩展方法。EKF的核心思想是在当前估计点附近对非线性函数进行一阶泰勒展开（局部线性化）：

1. 预测：
   $${\hat{x}}_{k|k-1}=f({\hat{x}}_{k-1|k-1},0),{\hat{y}}_{k|k-1}=h({\hat{x}}_{k|k-1},0)\text{\hspace{1em}(4)}$$
   状态和观测的预测值直接通过非线性函数计算。

2. 线性化：计算非线性函数在当前估计点(${\hat{x}}_{k-1|k-1}$和${\hat{x}}_{k|k-1}$)的雅可比矩阵（Jacobian）：
   $$F_{k-1}=\frac{\partial f}{\partial x}{|}_{{\hat{x}}_{k-1|k-1}},H_k=\frac{\partial h}{\partial x}{|}_{{\hat{x}}_{k|k-1}}\text{\hspace{1em}(5)}$$

3. 协方差预测与更新：使用线性化后的雅可比矩阵$F_{k-1}$和$H_k$替代KF中的$F$和$H$，计算先验协方差$P_{k|k-1}$、观测预测协方差$S_k$、卡尔曼增益$K_k$、后验协方差$P_{k|k}$。状态更新公式保持不变。
   $$P_{k|k-1}=F_{k-1}{P}_{k-1|k-1}{F}_{k-1}^T+Q,S_k=H_k{P}_{k|k-1}{H}_k^T+R,K_k=P_{k|k-1}{H}_k^T{S}_k^{-1},P_{k|k}=P_{k|k-1}-K_k{S}_k{K}_k^T\text{\hspace{1em}(6)}$$

总的来说，EKF具有如下局限性：

1. 线性近似误差：一阶泰勒展开仅在估计点附近小范围内有效。对于强非线性系统或估计误差较大时，线性近似失效，导致性能下降甚至发散。
2. 模型依赖性强：性能严重依赖于精确已知的非线性函数$f,h$（用于计算预测值和雅可比矩阵）以及噪声协方差$Q,R$（用于协方差传播和KG计算）。任何模型失配都会直接影响雅可比矩阵和协方差的计算，进而导致KG不准确，最终降低估计精度。
3. 雅可比矩阵计算：需要推导和计算非线性函数的导数，对于复杂函数可能繁琐且易错。
4. 数值稳定性：协方差矩阵需要保持正定，在迭代过程中可能因数值误差或强非线性而失去正定性。

2.3 相关工作：深度学习与状态空间模型的融合

将深度学习（特别是DNN）与状态空间模型结合是一个活跃的研究领域。KalmanNet提出之前和同期，已有多种尝试，主要思路可归纳如下：

1. 学习SS模型参数

• 传统方法：使用数据通过期望最大化（EM）、贝叶斯方法或直接优化来估计SS模型的未知参数（如$F,H,Q,R$）。这些方法通常假设参数化模型形式（如线性、高斯），限制了其处理复杂非线性和非高斯的能力。
• DNN方法：使用DNN（如RNN）从数据中学习状态转移函数$f$或观测函数$h$的参数，或者学习整个SS模型。例如，DeepAR等深度状态空间模型。这些方法侧重于模型学习本身，其滤波/平滑性能依赖于学习到的模型的质量。

2. 学习潜在空间中的SS模型

使用编码器DNN将高维/复杂观测（如图像）映射到一个低维潜在空间，并假设该潜在空间服从一个简单的（通常是线性高斯）SS模型。在潜在空间中使用KF/EKF进行状态跟踪，再通过解码器DNN将估计的状态映射回观测空间。整个系统可以端到端训练。这类方法（如KFNet）主要解决观测模型$h$复杂/难以解析表达的问题（如视觉观测），但假设状态转移$f$在潜在空间中是简单的线性模型。KalmanNet则侧重于状态空间本身动态($f$)的非线性和不确定性，并利用部分已知的$f$和$h$。

3. 变分推断与序列蒙特卡洛

利用变分自编码器（VAE）框架，将状态估计视为变分推断问题，通过优化参数化后验来近似真实后验分布。或者将PF与DNN结合，例如使用DNN学习建议分布（Proposal Distribution）或替换PF中的组件。这类方法（如Deep Kalman Filters，VRNN）功能强大，但通常计算复杂，难以满足严格的实时在线滤波要求，且可解释性相对较低。KalmanNet保持了KF的递归流程，推理速度快。

4. 端到端学习状态估计映射

最直接的方法是用一个RNN（如LSTM、GRU）直接将观测序列$y_{1:k}$映射到当前状态估计${\hat{x}}_{k|k}$。或者，结合一些MB元素，例如先用已知的$f$计算先验估计${\hat{x}}_{k|k-1}$，再用RNN学习从先验到后验的增量$\Delta x_k={\hat{x}}_{k|k}-{\hat{x}}_{k|k-1}$（论文中称为MBRNN）。这些纯粹或准DD方法缺乏KalmanNet中KF结构带来的归纳偏置（inductive bias）和可解释性，通常需要更多数据，且在模型部分已知时难以充分利用领域知识。

5. 神经增强传统算法

与KalmanNet最接近的思路是（Combining generative and discriminative models for hybrid inference），其将图神经网络（GNN）与已知精确SS模型的卡尔曼平滑器并行运行，通过神经模块增强平滑结果。但它是为离线平滑设计的，计算量大（涉及整个时间窗上的迭代消息传递），不适合在线滤波。KalmanNet则是将RNN深度集成到在线EKF的递归流程中，直接替代关键计算模块（KG），结构更紧耦合，专为实时滤波优化。

与上述方法相比，KalmanNet具有鲜明的特色：

• 聚焦在线滤波，专为实时状态估计设计；
• 明确假设状态转移$f$和观测$h$是部分已知的（即使近似），并将其作为已知结构融入算法骨架，不试图学习整个模型，也不将状态映射到另一个潜在空间；
• 学习关键环节（KG）：创新性地识别并替换EKF流程中最依赖噪声统计和易受模型失配影响的环节——卡尔曼增益的计算；
• 保持KF流程与可解释性：整体架构清晰遵循预测-更新流程，中间变量（先验/后验估计、新息）具有明确的物理意义；
• 高效与轻量：设计的RNN模块相对紧凑，旨在保持与EKF相当甚至更低的计算复杂度，适合嵌入式部署。

2.4 问题定义：部分已知动态下的滤波

KalmanNet针对的核心问题是：在满足以下条件的动态系统中，进行实时的、在线的状态估计（滤波）：

1. 部分已知SS模型：状态转移函数$f$和观测函数$h$是已知的（或可以获得其物理近似模型）。这些函数可能是非线性的。
2. 未知噪声统计：过程噪声协方差$Q$和观测噪声协方差$R$未知。
3. 可能存在模型失配：已知/使用的$f$和$h$可能与真实动态存在偏差（例如，物理模型的简化、离散化误差、传感器标定误差）。
4. 有标签数据可用：在算法设计（训练）阶段，可以获得包含观测序列$y_{1:T}$和对应真实状态序列$x_{1:T}$（ground truth）的数据集。这些真值可以通过额外传感器、离线高精度算法或其他手段获得。
5. 计算效率要求：推理（估计）过程的计算复杂度应与MB滤波方法（如EKF）相当，以适应实时性要求和硬件受限设备（如移动机器人、无人机）。

KalmanNet的目标效果是：在仅部分已知模型且存在噪声和失配的情况下，通过学习，实现接近或达到拥有完全精确模型和噪声信息的MBKF/EKF的性能（MMSE），同时超越存在模型失配的MB方法以及纯粹DD的RNN方法，并保持计算高效性和一定程度的可解释性。

三、KalmanNet技术路线解析

本节将深入解析KalmanNet的核心技术路线，包括其高层架构设计理念、关键输入特征的选择、两种具体的RNN实现方案以及训练算法细节，并讨论其优势、设计考量和与相关方法的区别。

3.1 高层架构设计

KalmanNet的设计哲学是保留已知，学习未知。它基于一个关键的观察：在扩展卡尔曼滤波（EKF）的流程中，虽然状态转移$f$和观测$h$（即使是非线性的）是部分已知并可以直接使用的，但卡尔曼增益（KG）$K_k$的计算高度依赖于精确的噪声协方差$Q,R$以及通过雅可比矩阵$F_{k-1},H_k$传播的二阶统计矩（$P_{k|k-1},S_k$）。恰恰是这个环节对模型失配（$f,h$不精确导致$F,H$不准）和噪声统计未知最为敏感，并且涉及数值上不稳定的矩阵求逆操作。

因此，KalmanNet的核心创新在于：保留EKF的整体递归流程和已知的非线性函数$f,h$，但用一个专门设计的、轻量级的循环神经网络（RNN）模块完全替代传统的、基于解析公式的卡尔曼增益计算器。图2展示了KalmanNet的顶层框图，与图1的标准EKF框图形成对比。

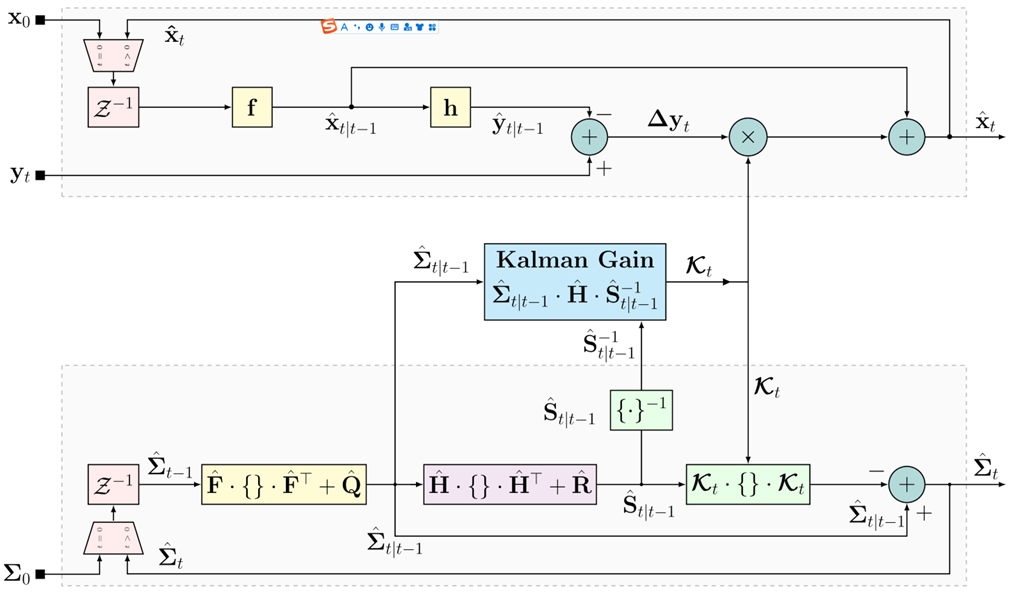
图1：标准EKF框图

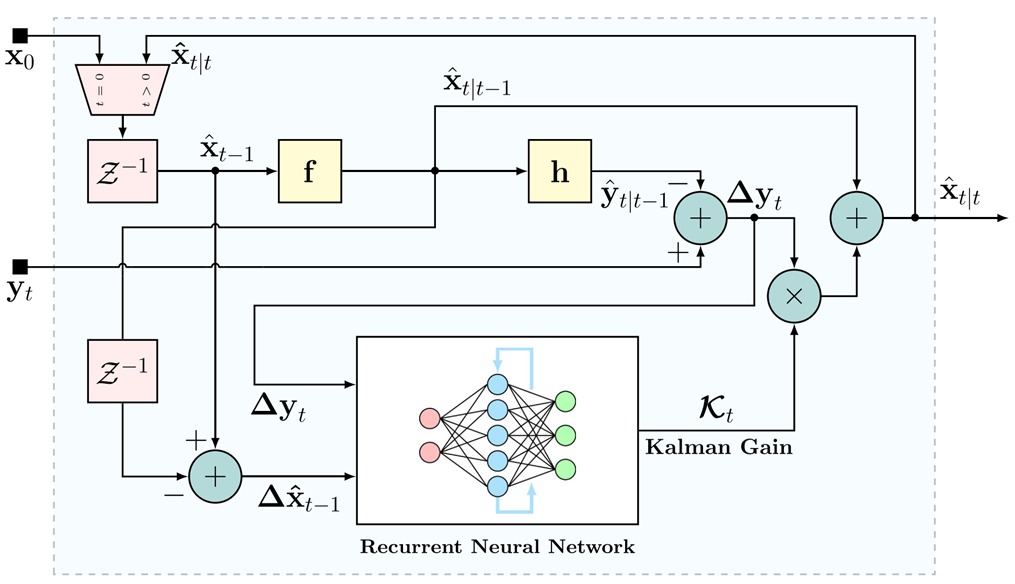
图2：KalmanNet框图。用循环神经网络（RNN）模块取代扩展卡尔曼滤波器（EKF）中基于模型的卡尔曼增益（KG）计算模块（图1）。循环神经网络（RNN）学习从观测值和状态估计得出的输入特征中计算卡尔曼增益。

KalmanNet工作流程如下所示：

1. 预测(Prediction-MB)：与EKF的预测步骤完全一致，使用已知的（可能是近似的）$f$和$h$：
   $${\hat{x}}_{k|k-1}=f({\hat{x}}_{k-1|k-1},0),{\hat{y}}_{k|k-1}=h({\hat{x}}_{k|k-1},0)\text{\hspace{1em}(7)}$$
   这一步是纯MB的，不涉及学习。

2. 新息计算(Innovation-MB)：计算观测新息，与EKF一致：
   $${\tilde{y}}_k=y_k-{\hat{y}}_{k|k-1}\text{\hspace{1em}(8)}$$

3. 特征提取：为了给RNN提供信息以学习KG，需要构造一组输入特征。这些特征旨在捕捉与未知噪声统计和模型不确定性相关的信息。论文提出了四个候选特征（F1-F4），实际应用中根据问题选择子集：

   • F1：观测差值$\Delta y_k=y_k-y_{k-1}$。反映观测信号本身的短期变化。
   • F2：新息差值${\tilde{y}}_k=y_k-{\hat{y}}_{k|k-1}$。即标准新息，反映观测预测的误差（这是最直接相关的特征）。
   • F3：前向状态演化差值$\Delta {\hat{x}}_{k|k}={\hat{x}}_{k|k}-{\hat{x}}_{k-1|k-1}$。反映连续两个后验状态估计之间的变化（在时间$k$，实际可用的是$\Delta {\hat{x}}_{k-1|k-1}$），表征状态演化的动态。
   • F4：前向更新差值$\Delta {\hat{x}}_{k|k|k-1}={\hat{x}}_{k|k}-{\hat{x}}_{k|k-1}$。反映后验状态估计相对于先验状态估计的更新量（在时间$k$，实际可用的是$\Delta {\hat{x}}_{k-1|k-1|k-2}$），表征基于新观测对先验估计的修正幅度。

   特征设计的意义：论文中指出，差值运算（F1,F3,F4）可以去除可预测的趋势成分，留下的时间序列主要受我们期望学习的噪声统计影响。F1和F3封装了状态演化过程的信息，F2和F4封装了状态估计不确定性的信息。经验表明，有效的特征组合包括{F2,F4}\{F2,F4\}{F2,F4}和{F1,F3,F4}\{F1,F3,F4\}{F1,F3,F4}，输入到RNN的特征向量通常是这些选择特征的拼接。

4. RNN计算卡尔曼增益：这是KalmanNet的DD学习核心。RNN模块接收当前时刻提取的特征向量${\varphi }_k$以及其自身的上一个隐藏状态$h_{k-1}$，输出当前时刻的卡尔曼增益矩阵$K_k$：
   $$K_k=\text{RNN}({\varphi }_k,h_{k-1})\text{\hspace{1em}(9)}$$
   RNN的作用是隐式地学习并跟踪计算最优KG所需的、与噪声统计和模型不确定性相关的隐含信息（替代了EKF中显式计算二阶矩和矩阵求逆的过程）。

5. 状态更新(State Update-MB)：使用RNN输出的$K_k$和步骤2计算的新息${\tilde{y}}_k$，按照标准KF/EKF的公式计算后验状态估计：
   $${\hat{x}}_{k|k}={\hat{x}}_{k|k-1}+K_k{\tilde{y}}_k\text{\hspace{1em}(10)}$$
   这一步在形式上是MB的，但其关键参数$K_k$是DD学习得到的。

6. 协方差更新：值得注意的是，在KalmanNet的标准流程中，没有显式地计算或更新后验误差协方差$P_{k|k}$(公式5b)。这是因为主要目标是状态估计${\hat{x}}_{k|k}$；$P_{k|k}$的计算传统上依赖于模型($F,H$或其近似)和KG，而在KalmanNet中KG是学习的，模型可能失配。如果需要状态估计的不确定性度量，可能需要额外的方法，或者利用学习到的KG本身隐含的信息，该论文的主要焦点是状态估计精度（MSE）。

总的来说，KalmanNet的关键优势包括以下几个方面：

• 绕过噪声模型和矩阵求逆：RNN直接学习输出KG，无需知道$Q,R$，也避免了$S_k^{-1}$的数值不稳定计算。
• 处理非线性和失配：RNN能够学习复杂的、非线性的映射关系，从而补偿$f,h$的近似误差以及模型失配的影响，即使在不进行局部线性化（无雅可比计算）的情况下。
• 保持效率：RNN模块设计为紧凑型，整体计算复杂度保持与EKF相当（线性于状态和观测维度），适合实时应用。
• 可解释性：保留了KF/EKF的预测-更新流程框架，输入特征和中间变量（新息、先验/后验估计）具有清晰的物理意义，RNN专注于学习KG这一特定功能。

3.2 RNN架构设计

RNN模块的核心任务是：利用历史信息和当前输入特征${\varphi }_k$，学习产生当前时刻最优（或次优）的卡尔曼增益$K_k$。论文提出了两种不同的RNN架构设计，权衡了灵活性、参数效率和与KF原理的贴合度。

3.2.1 架构1：隐式联合跟踪

设计理念：利用RNN（特别是GRU）固有的内部状态($h_k$)来隐式地、联合地跟踪计算KG所需的所有隐含信息（可以理解为替代了传统KF中需要跟踪的多个二阶统计矩$Q,P_{k|k-1},S_k$以及潜在的$R$等）。不强制要求RNN状态与特定统计矩一一对应。

结构如下：

1. 输入层(Input Layer)：一个全连接层（FC），接收输入特征向量${\varphi }_k$（例如{F2,F4}\{F2,F4\}{F2,F4}），并将其映射到更高维或更适合RNN处理的空间。输出记为${\varphi }_k^{\text{fc}}$。
2. RNN层(RNN Layer)：使用门控循环单元（GRU）。GRU通过更新门（Update Gate）和重置门（Reset Gate）机制，能有效地捕捉时间依赖关系并缓解标准RNN的梯度消失问题。GRU的隐藏状态$h_k$是其记忆核心。$h_k$的维度通常设置为远大于实际需要跟踪的统计矩维度（例如$d_h=256$），以提供足够的容量和冗余来学习复杂的动态关系。可以堆叠多层GRU以增加模型能力。
3. 输出层(Output Layer)：一个全连接层，接收GRU的隐藏状态$h_k$，并将其映射到卡尔曼增益$K_k$的向量化形式$\text{vec}(K_k)$。输出层通常包含$m\times n$个神经元（$m$为状态维度，$n$为观测维度）。

优点：结构简单通用，灵活性高，能够学习复杂的、可能不严格遵循KF矩传播规则的依赖关系。
缺点：参数较多（GRU参数随$d_h$平方增长），存在过参数化（Over-parameterization）风险，可解释性相对较弱。$d_h$需要根据问题经验设定。

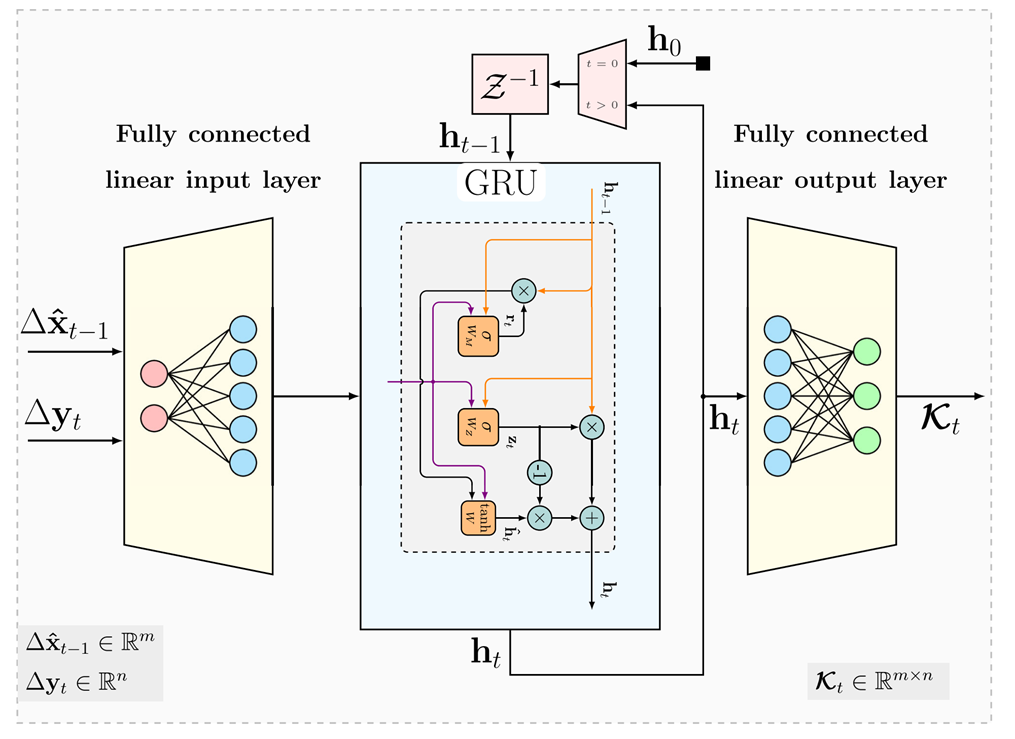
图3：卡尔曼网络循环神经网络（RNN）框图（架构1）。由一个全连接输入层组成，随后是一个门控循环单元（GRU）层（展示了内部门：重置门、更新门、候选激活）以及一个输出全连接层。所示的输入特征为F2和F4。

3.2.2 架构2：显式分离跟踪

设计理念：更紧密地遵循传统KF中KG的计算流程（$K_k=P_{k|k-1}{H}^T{S}_k^{-1},S_k=H{P}_{k|k-1}{H}^T+R,P_{k|k-1}=F{P}_{k-1|k-1}{F}^T+Q$），将计算分解为几个步骤，并为KF中涉及的关键未知二阶统计矩（$Q,P_{k|k-1},S_k$）设计独立的、专用的RNN模块进行显式跟踪和学习。目标是更直接地融入KF的结构化知识。

结构：该架构包含三个主要的GRU模块，通过全连接层连接，并按KF的计算流组织：

1. GRU_Q(跟踪过程噪声协方差)：第一个GRU模块负责学习/跟踪过程噪声协方差$Q$（或其相关信息）。它接收输入特征${\varphi }_k$（通常是所有F1-F4）和一个FC输入层。其隐藏状态$h_{Q,k}$旨在表示$Q$（或其向量化形式$\text{vec}(Q)$的时变或状态依赖特性）。输出一个FC层产生${\hat{Q}}_k$的估计（向量化）。
2. GRU_Σ(跟踪先验误差协方差)：第二个GRU模块负责学习/跟踪先验误差协方差$P_{k|k-1}$。它的输入不仅包括原始特征${\varphi }_k$（通过另一个FC层），更重要的是，它接收来自${\hat{Q}}_k$的信息（通过一个FC层）以及上一个时刻的后验协方差估计${\hat{P}}_{k-1|k-1}$。其隐藏状态$h_{\Sigma ,k}$旨在表示$P_{k|k-1}$。输出一个FC层产生${\hat{P}}_{k|k-1}$的估计。
3. GRU_S(跟踪观测预测协方差)：第三个GRU模块负责学习/跟踪观测预测协方差$S_k$（或其相关信息）。它的输入包括特征${\varphi }_k$（通过FC层）、来自${\hat{P}}_{k|k-1}$的信息（通过FC层）以及潜在的$R$信息（因为$S_k$隐含依赖$R$）。其隐藏状态$h_{S,k}$旨在表示$S_k$。输出一个FC层产生${\hat{S}}_k$的估计（向量化）。
4. 计算卡尔曼增益(Computing KG)：最后，按照KF公式（但不一定严格求逆），利用${\hat{P}}_{k|k-1}$、已知的（或近似的）观测矩阵$H$（或其线性化$H_k$）、以及${\hat{S}}_k$来计算近似的卡尔曼增益。论文中未明确说明具体计算方式，但可以理解为通过一个（或多个）FC层学习以下映射：
   $$K_k=\text{FC}({\hat{P}}_{k|k-1},H,{\hat{S}}_k)\text{\hspace{1em}(11)}$$
   这个FC层隐式地学习了“除以${\hat{S}}_k$”的操作（求逆的替代）。

优点：参数效率高（显式分解，维度由$m,n$决定，远小于架构1的$d_h$），更直接地结合了KF的结构化知识，可解释性相对更强（每个GRU对应一个KF中的关键统计量）。
缺点：结构更复杂，模块间的连接需要精心设计（非标准），灵活性可能较低（假设KG计算严格遵循KF流程的分解步骤，可能限制了其学习更复杂补偿机制的能力）。

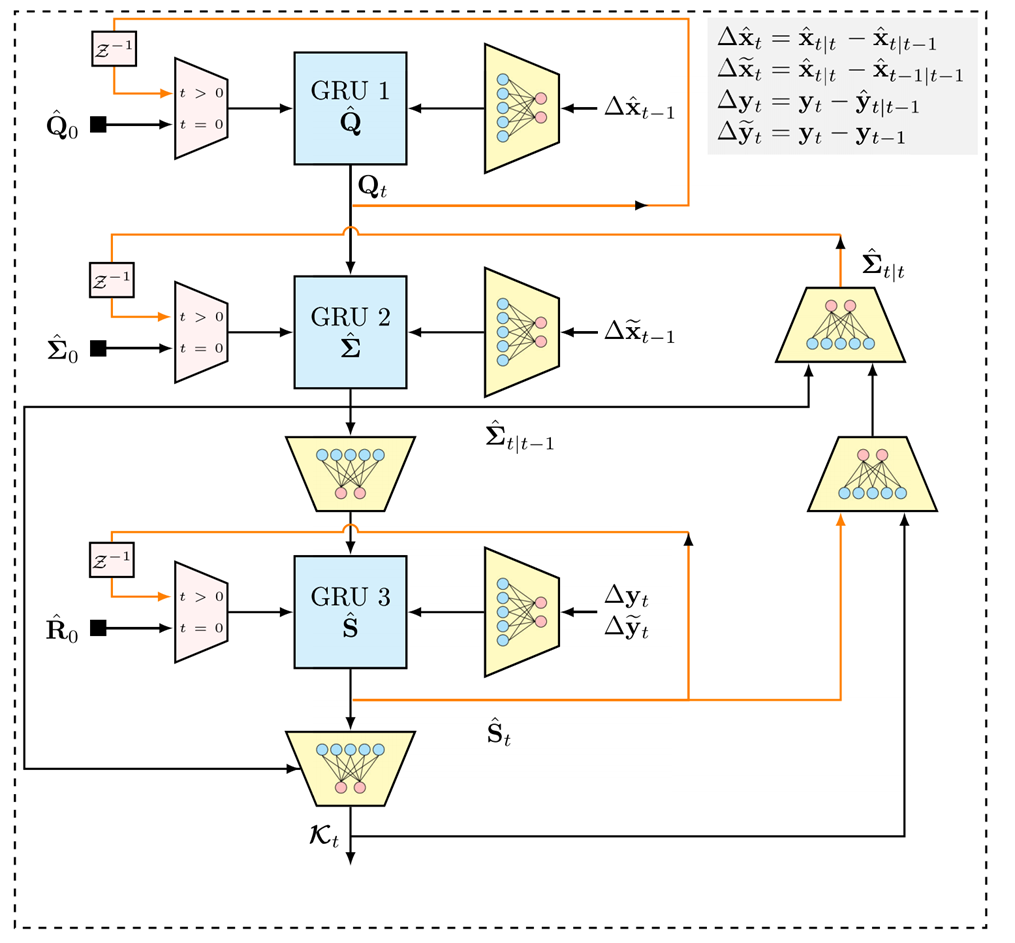
图4：卡尔曼网络循环神经网络模块框图（架构2）。输入特征用于通过专用的全连接层更新三个门控循环单元（GRU）：GRU_Q、GRU_Σ、GRU_S。输出通过全连接层进行组合，以计算学习到的卡尔曼增益。

架构选择：论文在实验中使用了两种架构。架构1（C1,C2,C3配置）更常用，尤其在输入特征组合探索和长序列实验中。架构2（C4配置）在特定实验（如合成非线性模型）中展现出良好的参数效率（例如，参数量从_500k降至25k）。选择哪种架构取决于具体问题的复杂度、对可解释性的要求以及对参数量的限制。

3.3 训练算法

KalmanNet使用带标签的数据集以监督学习的方式进行端到端（End-to-End）训练。

数据集

包含$N$条轨迹的数据集D={T1,T2,...,TN}\mathcal{D}=\{\mathcal{T}_{1},\mathcal{T}_{2},...,\mathcal{T}_{N}\}D={T1​,T2​,...,TN​}。每条轨迹Ti={y1:Ti(i),x1:Ti(i)}\mathcal{T}_{i}=\{y_{1:T_{i}}^{(i)},x_{1:T_{i}}^{(i)}\}Ti​={y1:Ti​(i)​,x1:Ti​(i)​}包含观测序列$y_{1:T_i}^{(i)}$和对应的真实状态序列$x_{1:T_i}^{(i)}$。轨迹长度$T_i$可以不同。

损失函数(Loss Function)

目标是最小化状态估计的误差。由于状态$x_k$是连续值向量，采用均方误差（MSE）作为损失函数。对于单条轨迹${\mathcal{T}}_i$，损失定义为：
$$\mathcal{L}(\theta ;{\mathcal{T}}_i)=\frac{1}{T_i}\sum _{k=1}^{T_i}\Vert {\hat{x}}_{k|k}(\theta ;{\mathcal{T}}_i)-x_k^{(i)}{\Vert }_2^2+\lambda \Vert \theta {\Vert }_2^2\text{\hspace{1em}(12)}$$
其中，

• ${\hat{x}}_{k|k}(\theta ;{\mathcal{T}}_i)$是KalmanNet在参数$\theta$下对轨迹${\mathcal{T}}_i$在时刻$k$的后验状态估计。
• $x_k^{(i)}$是时刻$k$的真实状态。
• $\lambda$是$L_2$正则化系数，用于防止过拟合。
• $\Vert \cdot {\Vert }_2$表示$L_2$范数。

整个训练集的损失通过小批量随机梯度下降（Mini-batch SGD）或其变体（如Adam）来最小化。批量损失为：
$${\mathcal{L}}_{\text{batch}}(\theta )=\frac{1}{B}\sum _{i\in \text{batch}}\mathcal{L}(\theta ;{\mathcal{T}}_i)\text{\hspace{1em}(13)}$$
其中，$B$是批量大小，$i$是当前批量中轨迹的索引。

端到端训练的关键

虽然RNN直接输出的是KG($K_k$)，但损失函数是作用在最终的状态估计${\hat{x}}_{k|k}$上。${\hat{x}}_{k|k}$是通过MB公式${\hat{x}}_{k|k}={\hat{x}}_{k|k-1}+K_k{\tilde{y}}_k$计算得到的。因此，需要通过这个MB公式将$\mathcal{L}$对$K_k$的梯度${\nabla }_{K_k}\mathcal{L}$反向传播到RNN模块。论文给出了这个梯度的显式形式：
$${\nabla }_{K_k}\mathcal{L}=\frac{2}{T_i}({\hat{x}}_{k|k}-x_k^{(i)}){\tilde{y}}_k^T\text{\hspace{1em}(14)}$$
其中，${\hat{x}}_{k|k}-x_k^{(i)}$（这是真实状态与先验估计的差，在训练时真实状态$x_k^{(i)}$已知）。这表明，即使没有外部提供的KG真值作为监督信号，通过最小化状态估计误差，也能有效地学习到KG的计算。

训练策略

BPTT

KalmanNet是一个具有双重递归的系统：(1)外部递归：KF的预测-更新流程。(2)内部递归：RNN自身的状态传递。训练这种递归网络的标准方法是通过BPTT（Backpropagation Through Time）。BPTT将网络在时间上展开，形成一个深度计算图，然后进行前向传播计算损失，再进行反向传播计算梯度。

处理长序列：BPTT变体

直接在整个长轨迹上应用BPTT（V1）可能计算昂贵且梯度不稳定（梯度爆炸/消失）。论文探讨了三种BPTT变体策略：

• V1(Full BPTT)：对整个轨迹进行完整的BPTT。计算开销最大，可能不稳定。
• V2(Truncated BPTT with Shuffling)：将长轨迹（如T=3000）分割成多个重叠或不重叠的短片段（如T=100）。在训练时，随机打乱这些片段，并对每个短片段独立应用BPTT（只在该片段内反向传播）。这大大降低了计算负担和内存需求。
• V3(Truncated BPTT with Fixed Length)：直接使用固定长度的短轨迹（如T=20）进行训练和BPTT。这适用于动态快速趋于稳态的系统（如线性系统）。

策略选择：论文建议的策略是先使用V2进行“热身”训练以稳定学习过程，然后再用V1进行微调。V3适用于特定场景。在实验中，不同的KalmanNet配置使用了不同的策略（C1:V3,C2:V1,C3:V2,C4:V1）。

优化器

使用Adam优化器进行参数更新。

训练优势

KalmanNet的训练相对高效。它只需要状态估计的真值，不需要提供KG的真值（这在实际中无法获得）。通过利用KF结构，它比纯端到端的RNN状态估计器收敛更快，所需数据更少。学习到的KG计算展现出良好的可迁移性：在短轨迹上训练的网络，可以很好地应用于显著长于训练长度的轨迹和不同的初始条件。

3.4 讨论与分析

KalmanNet作为创新的混合MB/DD滤波框架，在非线性动态系统状态估计中展现出多方面的显著优势。

克服传统模型基（MB）方法局限

其核心突破在于对非线性特性的处理能力与模型依赖性的弱化。相较于扩展卡尔曼滤波（EKF）依赖局部线性化近似的固有缺陷，KalmanNet通过递归神经网络（RNN）构建全局非线性补偿机制，能够更精准地处理强非线性系统动态，避免了线性化引入的局部近似误差。该框架无需显式噪声模型的设计，直接通过数据学习卡尔曼增益（KG），绕过了对过程噪声和观测噪声协方差矩阵的精确先验知识依赖，从根本上解决了传统方法中噪声统计特性估计的难题。即使存在模型失配（即系统矩阵和观测矩阵与真实系统存在近似误差）时，RNN仍能通过自适应学习调整卡尔曼增益，有效补偿模型不匹配带来的性能下降，而EKF等纯MB滤波器在此类场景下性能会显著退化。此外，RNN计算卡尔曼增益的机制替代了传统公式中的矩阵求逆操作，尤其在高维状态空间中大幅提升了数值稳定性，避免了因矩阵奇异性导致的计算风险。

与纯粹数据驱动（DD）方法对比优势

KalmanNet的优势体现在数据效率、可解释性、性能及计算复杂度的平衡上。该框架充分利用已知的系统动态和观测模型作为强归纳偏置，相较于直接学习状态映射的纯RNN模型，显著降低了对训练数据量的需求，收敛速度更快，更适合实际应用中数据有限的场景。在保持卡尔曼滤波（KF）经典的“预测-更新”流程基础上，其输入特征（如新息、状态差值）和输出（卡尔曼增益）均具有明确的物理意义，网络仅专注于学习卡尔曼增益计算这一特定功能模块，而非整个黑盒映射，从而兼具数据驱动的灵活性与模型驱动的可解释性。从性能表现来看，在线性高斯完全信息场景下，KalmanNet能严格达到最优KF的最小均方误差（MMSE）；而在非线性系统或模型失配条件下，其估计精度显著优于纯DD的RNN模型。在计算效率方面，精心设计的RNN模块结构紧凑，整体推理复杂度与EKF相当，呈线性于状态/观测维度和RNN规模，适用于嵌入式实时系统，避免了大型神经网络带来的高推理开销问题。

与相关混合方法的独特性

KalmanNet的独特性体现在其对原始状态空间的直接操作与功能模块的聚焦设计。不同于部分混合方法通过学习低维潜在空间及其简单状态空间（SS）模型来处理高维观测（如图像）的目标，KalmanNet直接在实际应用的原始状态空间中运行，充分利用部分已知的系统动态和观测模型结构。该框架并不试图学习系统矩阵和观测矩阵本身，而是在认可其近似有效性的基础上，专注于学习补偿其不足及未知噪声的卡尔曼增益计算模块，这种设计策略既保留了模型驱动方法的先验知识优势，又通过数据驱动弥补了模型不精确性。相较于结合深度神经网络（DNN）的变分推断或粒子滤波（PF）方法，KalmanNet保持了KF高效的递归框架，专为在线滤波设计，计算开销远低于基于采样的PF或需要迭代推断的变分方法，结构更简洁直观。与针对离线平滑任务的神经增强方法相比，KalmanNet深度集成于在线滤波流程，通过替换卡尔曼增益计算模块实现实时估计，避免了离线方法的高计算成本。

潜在优势与应用场景

KalmanNet的实时性设计使其成为无人机、自动驾驶车辆、机器人等移动设备状态估计的理想选择，论文中真实赛车实验验证了其在硬件资源受限环境下的高效性。尽管当前框架未显式计算后验协方差，但学习到的卡尔曼增益与传统KF中的后验协方差存在内在关联，其大小和方向隐式反映了估计不确定性，为未来结合不确定性量化提供了探索空间。该框架还具有良好的扩展性，可通过端到端训练学习未知的系统动态或观测模型，利用预测观测进行无监督/自监督学习（尤其适用于时变模型参数场景），并可扩展至平滑（如Rauch-Tung-Striebel平滑器）和预测任务，展现出强大的应用潜力。

局限性

然而，KalmanNet也存在一定局限性：

1. 其性能依赖于部分已知的系统动态和观测模型近似，若这些先验信息完全未知或严重不准确，尽管仍优于纯MB方法，但可能不及某些依赖大量数据训练的纯DD方法，论文提出通过数据预估计或学习这些函数作为未来改进方向。
2. 作为监督学习方法，其训练需要带状态真值的标注数据，这在某些实际场景（如复杂物理系统）中获取成本较高。
3. RNN架构的选择（如不同类型的递归单元）及特征工程（输入特征F1-F4的设计）需要结合具体问题调优，存在一定经验依赖性。
4. 从理论层面看，作为混合方法，其收敛性、稳定性等理论分析较经典KF更为复杂，当前研究主要基于实证结果，尚未形成完整的理论体系。

KalmanNet通过模型驱动与数据驱动的深度融合，为部分已知非线性动态系统的实时状态估计提供了创新解决方案。其在强非线性处理、模型失配鲁棒性、计算效率及可解释性方面的优势，使其特别适用于存在模型不确定性和噪声统计未知的挑战性环境。尽管存在对先验模型的依赖性和理论分析的不足，但该框架通过平衡先验知识与数据学习，开辟了实时状态估计领域的新路径，展现出从理论研究到工程应用的广阔前景。

四、实验与结果分析

本节将系统梳理论文中对KalmanNet进行的广泛而深入的数值实验。实验设计覆盖了多种场景：从基础的线性模型到复杂的非线性混沌系统，再到真实世界的传感器数据集；从完全信息（模型精确已知）到各种形式的模型失配（部分信息）。KalmanNet的性能将与多种基线方法进行严格对比，包括基于模型（MB）的经典滤波器（KF,EKF,UKF,PF）和纯粹数据驱动（DD）的方法（如Vanilla RNN）。评估的核心指标是状态估计的均方误差（MSE），部分实验还报告了运行时间。实验结果充分验证了KalmanNet在克服非线性和模型失配、实现高效准确状态估计方面的显著优势。

4.1 实验设置

评估指标

主要评估指标是状态估计的均方误差（MSE），单位为分贝（dB）：$\text{MSE(dB)}=10{\log }_{10}\left(\frac{1}{T}{\sum }_{k=1}^T\Vert {\hat{x}}_{k|k}-x_k{\Vert }_2^2\right)$。数值越低表示估计越准确。部分实验报告了MSE的均值和标准差（$\mu \pm \sigma$）。

噪声设置

在合成数据实验中，过程噪声和观测噪声通常假设为对角协方差矩阵：
$$Q=q^2\cdot I_m,R=r^2\cdot I_n\text{\hspace{1em}(15)}$$
实验常通过改变$q^2$（固定$r^2$）或改变$1/r^2\text{(dB)}$来模拟不同的观测噪声水平。

信息等级

• 完全信息(Full Information)：KalmanNet使用的$f,h$与生成数据的真实模型完全一致。其MB对比算法（KF/EKF/UKF）使用精确的$Q,R$。
• 部分信息(Partial Information)/模型失配(Model Mismatch)：KalmanNet和MB对比算法使用的$f,h$与真实模型存在偏差（例如，旋转矩阵、泰勒展开阶数不足、离散化近似误差）。MB算法可能使用真实或设计错误的$Q,R$（论文中通常会优化MB算法的参数以展现其最好性能）。

KalmanNet配置

论文使用了四种配置进行实验：

• C1: 架构1(隐式)，输入特征{F2,F4}，训练算法V3(短轨迹BPTT)。
• C2: 架构1(隐式)，输入特征{F2,F4}，训练算法V1(全BPTT)。
• C3: 架构1(隐式)，输入特征{F1,F3,F4}，训练算法V2(截断BPTT+打乱)。
• C4: 架构2(显式)，输入特征{F1,F2,F3,F4}，训练算法V1(全BPTT)。

基线方法(Baselines)

• MB：KF(线性), EKF, UKF, PF(100粒子)。
• DD：Vanilla RNN(端到端状态估计), MBRNN(用$f$计算先验，RNN学习后验增量)。
• Oracle/理想情况：使用真实模型和真实噪声统计的MB滤波器（如KF或EKF），代表该场景下可达到的理论最优或接近最优性能（MMSE基准）。

优化

对于MB方法，在模型失配情况下，通常使用网格搜索（Grid Search）在可用数据上调优其噪声协方差参数（$Q,R$或其缩放因子），以展现其在该失配模型下可能的最佳性能。PF参数（如粒子数、建议分布）也经过调整。KalmanNet使用Adam优化器训练。

4.2 线性状态空间模型

4.2.1 实验1：完全信息-达到MMSE

实验参数设置：线性高斯SS模型($f=Fx+w,h=Hx+v$)。$F$采用可控标准型（Controllable Canonical Form），$H$为其逆标准型。$1/r^2=30\text{dB}$，KalmanNet使用配置C1。
测试参数设置：变量测试不同系统维度($m=2,4,8,16$)和不同轨迹长度($T_{\text{train}}=20,T_{\text{test}}=20,200,2000$)。

实验结果：如图5所示，KalmanNet的MSE曲线与MBKF的曲线几乎完全重合。在所有测试的维度($m=2,4,8,16$)和轨迹长度下，KalmanNet都达到了与MBKF相同的MSE性能。在$T_{\text{train}}=20$的短轨迹上训练的KalmanNet，在$T_{\text{test}}=2000$的长轨迹和不同初始条件下测试，其MSE仍然等于MBKF的MMSE。

结论：该实验有力证明了KalmanNet在理想（线性高斯、完全信息）场景下的正确性和最优性。KalmanNet成功地从数据中学习到了如何执行最优卡尔曼滤波，其性能不依赖于训练轨迹的长度或初始条件，只依赖于SS模型本身。这表明RNN学习到的KG计算机制在本质上是正确的。

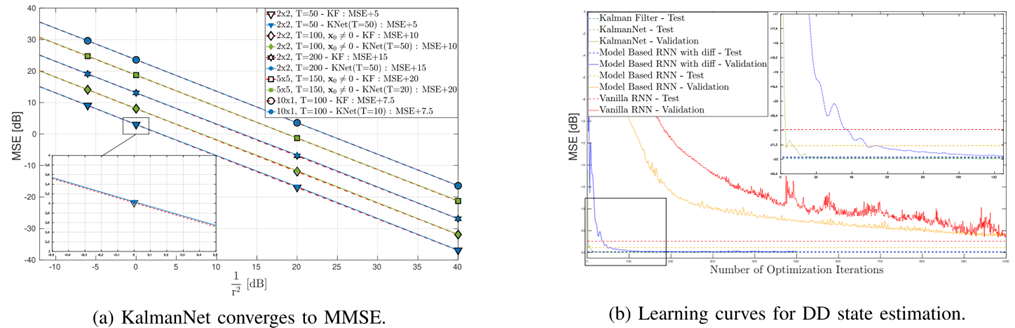
图 5：具有完整信息的线性SS模型

4.2.2 实验2：架构与特征有效性验证

实验参数设置：$m=2$线性系统，完全信息。比较KalmanNet(C1)与两种基于RNN的端到端状态估计器：

• Vanilla RNN: 直接映射$y_{1:k}$到${\hat{x}}_{k|k}$；
• MBRNN: 先用$f$（即$F$）计算先验估计${\hat{x}}_{k|k-1}$，然后使用一个与KalmanNet内部RNN相同架构的RNN来估计从先验到后验的增量$\Delta x_k={\hat{x}}_{k|k}-{\hat{x}}_{k|k-1}$，最终${\hat{x}}_{k|k}={\hat{x}}_{k|k-1}+\Delta x_k$。

训练：所有RNN使用单层GRU，相同超参数，在$T_{\text{train}}=20$的短轨迹上训练。在相同长度($T_{\text{test}}=20$)的测试轨迹上绘制学习曲线。另外，在$T_{\text{test}}=2000$的长轨迹上测试预训练好的模型（训练长度为$T_{\text{train}}=20$）。

实验结果：

• Vanilla RNN收敛慢且MSE高（远高于MMSE）。
• MBRNN利用了$f$知识，性能优于Vanilla RNN，但仍收敛较慢且未能达到MMSE。
• 将MBRNN的输入改为特征{F2，F4}（即KalmanNet的输入）后，其收敛速度显著加快（图中“MBRNN w/F2,F4”），表明这些特征包含了对状态估计至关重要的信息。
• KalmanNet(学习KG)的收敛速度最快，且最终达到了MMSE（与KF重合）。
• 在$T_{\text{test}}=2000$的长轨迹上，KalmanNet(C1)依然保持达到MMSE；Vanilla RNN和MBRNN的MSE比MMSE差>50dB，性能崩溃；MBRNN w/F2，F4性能大幅改善，MSE接近KalmanNet/KF（差距很小）。

结论：该实验验证了KalmanNet设计的关键要素：

1. 融入已知模型($f$)能提升DD方法的性能（MBRNN>Vanilla RNN）。
2. 精心设计的输入特征（F2,F4）能显著加速学习并提升性能（MBRNN w/F2,F4>>MBRNN）。
3. 学习KG（而非直接学习状态增量）是KalmanNet能达到最优性能（MMSE）且具备强泛化能力（训练短轨迹泛化到长轨迹）的关键原因。学习KG似乎让网络更聚焦于学习噪声统计和不确定性权重，而非整个状态动态。

4.2.3 实验3：部分信息-模型失配

实验设置：$m=2$线性系统，同时引入了模型失配：

1. 状态转移失配：数据由旋转后的状态矩阵$F_{\text{rot}}=RF$生成（$R$为旋转矩阵，旋转角$\theta =10^{\circ }$）。滤波器使用未旋转的$F$（可控标准型），$Q=0.1I_2,R=I_2$，$1/r^2=30\text{dB}$，KalmanNet使用C2。
2. 观测失配：数据由旋转$H_{\text{rot}}=RH$的观测矩阵生成。滤波器使用$H=I_2$（单位阵，代表传感器未对准约5.5%），$Q=0.1I_2,R=I_2$，$1/r^2=30\text{dB}$，KalmanNet使用C2。额外实验：先用数据估计观测矩阵$\hat{H}$，再用$\hat{H}$运行KalmanNet。

实验结果：

• 状态转移失配：使用错误模型$F$的MBKF性能显著下降（MSE比使用真实$F_{\text{rot}}$的Oracle KF差约3-6dB）；KalmanNet(使用$F$)显著优于使用$F$的MBKF，性能提升约3dB，其MSE非常接近Oracle KF(使用真实$F_{\text{rot}}$)的MMSE。
• 观测失配：使用错误模型$H=I_2$的MBKF性能很差；KalmanNet(使用$H=I_2$)的性能明显优于错误的MBKF，并且其MSE曲线逐渐收敛到接近Oracle KF(使用真实$H_{\text{rot}}$)的MMSE；当KalmanNet使用估计出的$\hat{H}$（代替$H=I_2$)时，其MSE达到了Oracle KF的MMSE。

结论：该实验充分展示了KalmanNet对模型失配的鲁棒性。即使在使用的$F$或$H$存在误差的情况下，KalmanNet通过学习KG，能够自适应地调整其更新行为，部分或完全补偿了模型误差带来的影响，其性能显著优于使用相同错误模型的传统MB滤波器。如果能够从数据中估计出部分模型参数（如$H$），KalmanNet可以进一步利用这些信息达到最优性能。这体现了其灵活性和兼容性。

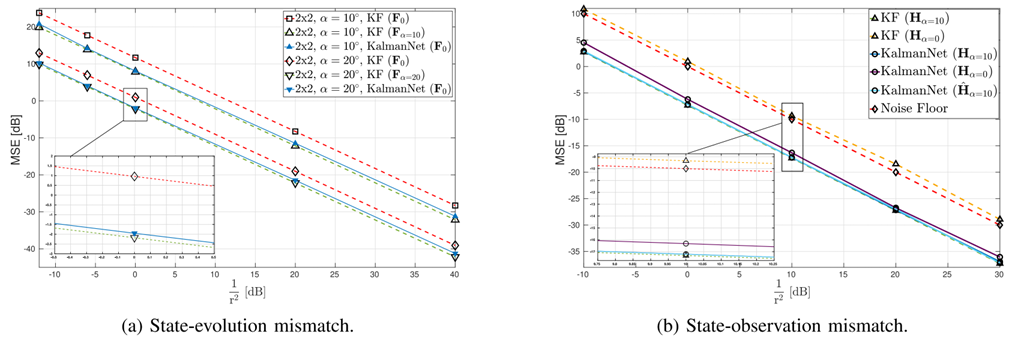
图 6：线性SS模型，部分信息

4.3 合成非线性模型

4.3.1 实验4：正弦-多项式模型

非线性模型定义为：
$$x_k=\sin (x_{k-1})+w_{k-1},y_k=x_k^2+v_k\text{\hspace{1em}(16)}$$
状态转移$f(x)=\sin (x)$是正弦函数（强非线性），观测$h(x)=x^2$是二次多项式（非线性）。具体参数见表II。$m=1,n=1$，$1/r^2=30\text{dB}$。KalmanNet使用架构2的配置C4。

实验结果：

• 完全信息场景：在低噪声区域($1/r^2$高)，EKF性能最好（接近该场景下能达到的MMSE），KalmanNet与之相当；在高噪声区域($1/r^2<20\text{dB}$)，EKF性能显著下降（由于非线性效应导致线性化失效），UKF和PF性能也较差，KalmanNet在高噪声下保持高性能，MSE显著低于所有MB方法（EKF，UKF，PF）。
• 模型失配场景：模型失配导致所有MB滤波器（EKF，UKF，PF）的性能严重下降；KalmanNet成功克服了模型失配，其MSE远优于所有MB方法（差距可达~10dB），且性能与完全信息下KalmanNet自身相比，仅有小幅下降。

结论：该实验证明了KalmanNet在强非线性和模型失配双重挑战下的强大优势。在低噪声完全信息下，KalmanNet能与经过良好调优的EKF竞争；在高噪声下，KalmanNet显著优于MB方法，表明其学习的KG能更好地处理非线性引起的非高斯不确定性；对模型失配具有极强的鲁棒性，性能损失远小于MB方法，RNN成功学习到了补偿模型误差的机制。

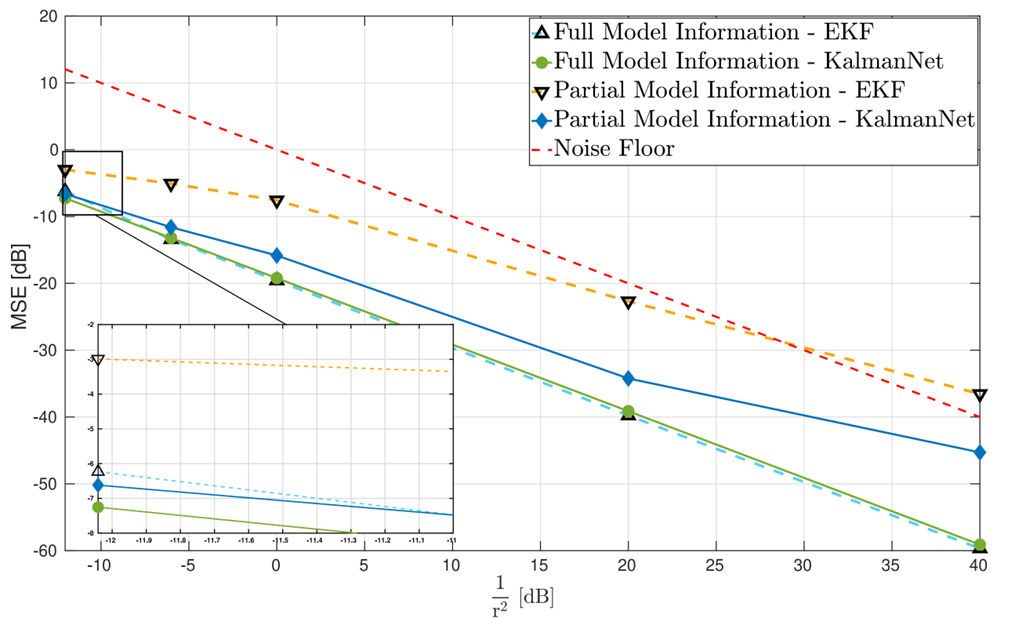
图 7：合成非线性状态空间模型（正弦状态演化和二次观测）。在完全信息下，卡尔曼网络（C4）在低噪声时与扩展卡尔曼滤波器（EKF）相当，在高噪声（分贝）时优于所有基于模型的滤波器（EKF、无迹卡尔曼滤波器（UKF）、粒子滤波器（PF））。在部分信息下，卡尔曼网络显著优于受模型不匹配影响的基于模型的滤波器。

4.4 Lorenz吸引子(混沌系统)

Lorenz吸引子是描述大气对流的经典三阶混沌系统，具有高度非线性、对初始条件敏感（蝴蝶效应）的特性。论文用它来模拟强非线性和连续时间系统离散化带来的挑战。

连续时间模型

$${\dot{x}}_1=\sigma (x_2-x_1),{\dot{x}}_2=x_1(\rho -x_3)-x_2,{\dot{x}}_3=x_1{x}_2-\beta x_3\text{\hspace{1em}(17)}$$
其中，$\sigma =10,\rho =28,\beta =8/3$（经典混沌参数）。

离散化

采用采样间隔$T_s=0.01$，并在$x_{k-1}$附近假设$\dot{x}$在短时间$T_s$内恒定。离散状态转移通过矩阵指数及其泰勒近似实现：
$$x_k=\exp (F_{k-1}{T}_s)x_{k-1}+w_{k-1},F_{k-1}=\frac{\partial \dot{x}}{\partial x}{|}_{x_{k-1}}\text{\hspace{1em}(18)}$$
其中，$p$是泰勒展开阶数。真实数据用$p=5$生成，$Q=0.1I_3$。

4.4.1 实验5：完全信息

实验设置：

• 场景1：观测模型$h(x)=x$（线性观测，$H=I_3$），$R=I_3$，$1/r^2=30\text{dB}$，KalmanNet使用C3。
• 场景2：观测模型$h(x)=[\sqrt{x_1^2+x_2^2+x_3^2},\arctan 2(x_2,x_1),\arctan 2(x_3,\sqrt{x_1^2+x_2^2}){]}^T$（球坐标非线性观测），$R=0.1I_3$，$1/r^2=10\text{dB}$，KalmanNet使用C4。

实验结果：

• 场景1（线性观测）：使用精确$F(p=5)$模型的EKF在调优$Q$后能达到较好性能（与Oracle接近）；UKF和PF性能较差；KalmanNet(C3,训练于$T_{\text{train}}=200$)的性能与调优后的EKF相当，并且优于UKF和PF。
• 场景2（非线性观测）：所有MB方法（EKF，UKF，PF）的性能都相对较差；KalmanNet(C4)显著优于所有MB方法(EKF，UKF，PF)。

结论：在完全信息下，KalmanNet在强非线性混沌系统上表现优异。对于相对简单的观测($h=I_3$)，能达到与精心调优的EKF相当的水平；对于复杂的非线性观测($h=$球坐标变换)，其性能明显优于所有MB基准，展示了其在处理复杂观测非线性方面的优势。

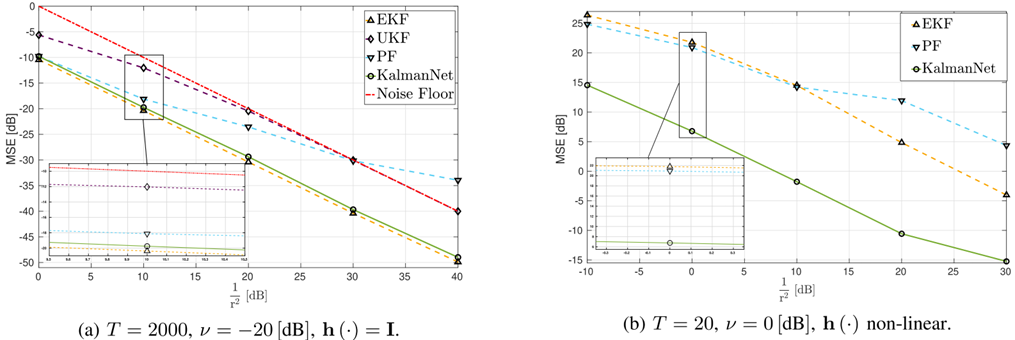
图 8: 具有完整信息的洛伦兹吸引子。(a) 含噪状态观测。卡尔曼网络（C3）实现了与调优后的扩展卡尔曼滤波器（EKF）相当的性能，并且优于无迹卡尔曼滤波器（UKF）/粒子滤波器（PF）。(b) 含噪非线性观测（球坐标）。卡尔曼网络（C4）显著优于所有模型基滤波器（EKF、UKF、PF）。

4.4.2 实验6：部分信息-多种失配

设计三种典型的模型失配场景，验证KalmanNet的鲁棒性：

场景1：状态转移失配

滤波器使用低阶泰勒近似($p=2$)的$F$，而数据由$p=5$生成。$Q=0.1I_3$，$R=I_3$，$1/r^2=30\text{dB}$，KalmanNet用C4。

结果：使用精确$F(p=5)$模型的EKF性能最好（基准）；使用错误$F(p=2)$模型的EKF、UKF、PF性能显著下降；KalmanNet(使用$F(p=2)$模型)部分克服了失配，其性能优于所有使用$F(p=2)$模型的MB方法(EKF，UKF，PF)，并且MSE介于使用$F(p=5)$的EKF和使用$F(p=2)$的EKF之间。

场景2：观测旋转失配

观测模型使用单位阵$H=I_3$，而数据由旋转$H_{\text{rot}}=RH$（$R$为随机旋转矩阵，失准角$\approx 5^{\circ }$）生成。$F$精确($p=5$)。$Q=0.1I_3,R=I_3$，$1/r^2=30\text{dB}$，KalmanNet用C3(在$T_{\text{train}}=200$训练)。

结果：微小的$H$观测旋转导致所有MB滤波器(EKF，UKF，PF)的性能严重劣化（MSE比无失配情况差很多）；KalmanNet(C3，训练于$T_{\text{train}}=200$)成功学习补偿了该失配，其MSE显著优于所有MB方法(差距可达数dB)。

场景3：采样失配

数据由高采样率($T_{s,\text{true}}=0.01$)的（近似）连续时间Lorenz系统生成，然后降采样($T_{s,\text{filter}}=0.1$)得到离散序列($k=1,2,...$)。滤波器使用基于$T_{s,\text{filter}}=0.1$设计的离散模型($F_{\text{approx}},Q_{\text{approx}}$)。这模拟了连续系统离散化引入的固有模型误差，无过程噪声，$R=0.1I_3$，$1/r^2=10\text{dB}$，KalmanNet用C4，对比MB-RNN(用$F_{\text{approx}}$计算先验，RNN学习后验增量)。

结果：所有MB滤波器(EKF，UKF，PF)和MB-RNN的性能都较差（MSE~-5.3-6.4dB）；KalmanNet(C4)显著优于所有对比方法，MSE达到约-11.3dB，取得了约5-6dB的处理增益；KalmanNet的估计轨迹明显更贴近真实状态，而EKF的轨迹发散严重。

结论：Lorenz吸引子的多种失配实验表明，无论是状态转移近似误差、观测旋转失准，还是连续-离散采样不匹配，都会导致传统MB方法性能显著下降甚至发散。而KalmanNet通过学习，能够有效补偿这些失配，性能显著优于传统MB方法以及简单的MB+RNN混合方法(MB-RNN)，同时保持了可满足实时需求的推理速度。

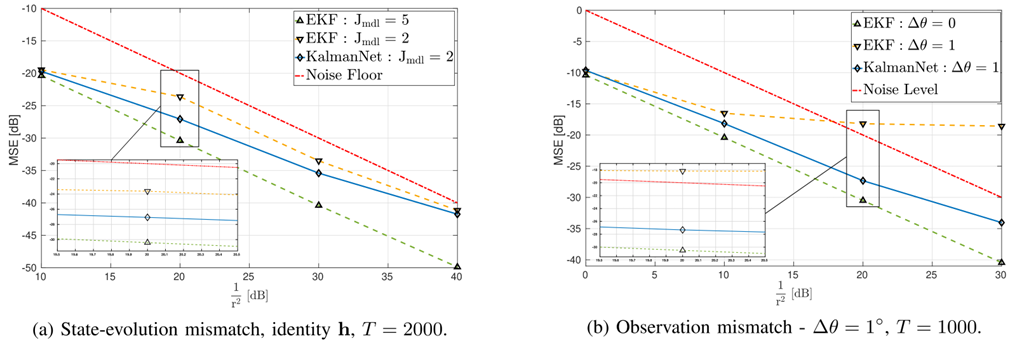
图 9：含部分信息的洛伦兹吸引子。(a) 状态演化失配（低阶泰勒展开与真实值对比）。卡尔曼网络（C4）部分克服了失配问题，表现优于基于模型的滤波器（扩展卡尔曼滤波器、无迹卡尔曼滤波器、粒子滤波器）。(b) 观测旋转失配。卡尔曼网络（C3）学会了补偿，显著优于对微小不对准敏感的基于模型的滤波器。（根据论文描述重现）。

图 10：具有采样失配的洛伦兹吸引子上跟踪性能的可视化（单轨迹）。卡尔曼网络（C4）紧密跟踪真实状态，而扩展卡尔曼滤波器（EKF）则显著发散。（根据论文描述重现）。

4.5 真实世界应用：密歇根NCLT数据集定位

任务背景

任务为使用密歇根大学NCLT数据集进行车辆定位。数据集包含Segway机器人搭载的多传感器（GPS、里程计等）数据和地面真值（激光SLAM生成的位置）。需要解决的问题为仅使用带噪声的里程计（速度）读数($y_k$）来估计车辆的2D位置($x_1,x_2$)和速度($x_3,x_4$)。这是一个极具挑战性的任务，因为里程计存在漂移，且没有直接的绝对位置测量（如GPS失效的室内环境）。

模型定义

模型采用线性Wiener速度模型（每个坐标轴独立）：
$$\left[\begin{array}{c}{x}_1(k)\\ x_3(k)\end{array}\right]=\left[\begin{array}{cc}1& T_s\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1(k-1)\\ x_3(k-1)\end{array}\right]+\left[\begin{array}{c}{T}_s^2/2\\ T_s\end{array}\right]w_1(k-1)$$
$$\left[\begin{array}{c}{x}_2(k)\\ x_4(k)\end{array}\right]=\left[\begin{array}{cc}1& T_s\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_2(k-1)\\ x_4(k-1)\end{array}\right]+\left[\begin{array}{c}{T}_s^2/2\\ T_s\end{array}\right]w_2(k-1)\text{\hspace{1em}(19)}$$
离散化($T_s=1\text{s}$采样间隔)后，合并为4维状态模型：
$$x_k=F{x}_{k-1}+w_{k-1},F=\left[\begin{array}{cc}{I}_2& T_s{I}_2\\ 0& I_2\end{array}\right],Q=q^2\left[\begin{array}{cc}{T}_s^4/4I_2& T_s^3/2I_2\\ T_s^3/2I_2& T_s^2{I}_2\end{array}\right]\text{\hspace{1em}(20)}$$
观测模型可表示为$y_k=H{x}_k+v_k$（带噪声的速度读数），即$H=[0I_2]$（针对单个坐标轴，组合后为4维状态2维观测)。由于观测只提供速度，位置估计会随时间累积漂移。

实验设置

• 数据来源：使用数据集中的一条轨迹(2012-01-22)，采样率1Hz，有效长度5556步。
• 数据分割：85%训练(23条$T=200$序列)，10%验证(2条$T=200$)，5%测试(1条$T=278$)。
• KalmanNet配置：使用C1。
• 对比方法：MBKF(需优化$q^2,r^2$)和Vanilla RNN。

实验结果

• 基线方法（速度积分）：单纯对速度积分（相当于假设速度读数完美且无噪声）的位置估计(${\hat{x}}_1,{\hat{x}}_2$)由于里程计漂移，轨迹严重偏离真值(MSE=25.47dB)。
• MBKF：即使调优了$q^2,r^2$，KF的位置估计仍然紧密跟随积分速度的轨迹，无法有效校正漂移，性能与基线相当甚至略差。
• Vanilla RNN：完全失效，无法产生有意义的位置估计(MSE=40.21dB)。
• KalmanNet：显著优于所有对比方法，MSE达到22.2dB，比MBKF和基线改善了约3.2dB；其估计轨迹明显更接近地面真值。

结论

这个真实世界的定位实验是KalmanNet价值的有力证明。它成功应用于真实传感器数据，这些数据并非由预设的SS模型精确生成。在仅依赖噪声大、易漂移的里程计这一挑战性条件下，KalmanNet通过学习，能够有效抑制漂移误差，获得比基于物理运动模型(Wiener)的MBKF更准确的位置估计，且显著优于纯DD方法(Vanilla RNN)。这体现了KalmanNet融合物理模型($f$-运动学)与数据驱动学习(补偿噪声模型不准和里程计缺陷)的混合策略在实际应用中的巨大优势。

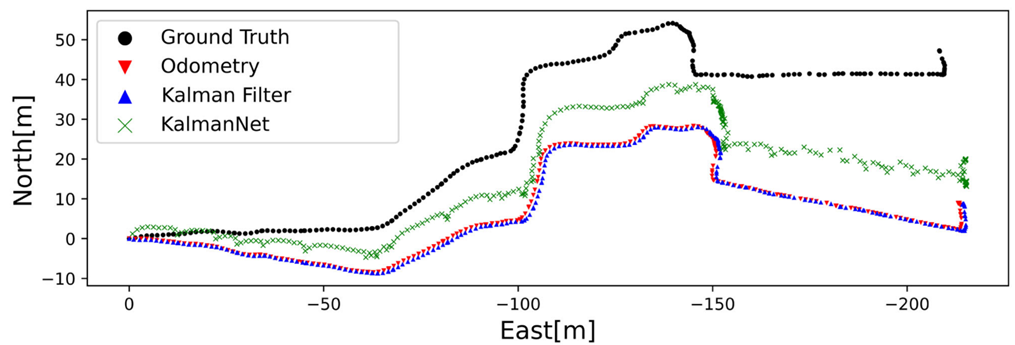
图 11：NCLT数据集定位结果（测试轨迹）。真实值与积分速度（基线）、MBKF和卡尔曼网络（C1）估计值的对比。卡尔曼网络显著减少了漂移，并提供了最准确的位置估计。（根据论文描述重现）

4.6 实验总结

通过涵盖线性/非线性、合成/真实、完全信息/部分信息（多种失配）的广泛实验，论文令人信服地证明了KalmanNet的有效性和优势：

1. 最优性：在线性高斯完全信息下，达到与最优KF相同的MMSE。
2. 鲁棒性：对状态转移模型失配($F$旋转、$p=2$ vs $p=5$)、观测模型失配($H$旋转$H_{\text{rot}}$、球坐标非线性)、连续-离散采样失配等，展现出强大的鲁棒性，性能显著优于存在相同失配的MB方法(EKF，UKF，PF)。
3. 非线性处理能力：在强非线性系统（正弦演化、Lorenz混沌）和复杂观测非线性（球坐标）下，性能优于或等于MB方法，尤其在模型失配或高噪声区域优势更明显。
4. 数据效率与泛化：相比纯DD方法(Vanilla RNN)，收敛更快，所需数据更少；在短轨迹上训练的网络能很好地泛化到长轨迹。
5. 计算效率：推理速度与EKF相当，远快于PF，适合实时应用（在自动驾驶赛车实验中得到验证）。
6. 实际应用价值：在真实世界里程计定位任务中，显著优于基于物理模型的MBKF和纯DD方法，有效抑制了传感器漂移。

KalmanNet成功地将模型驱动方法的可解释性、数据效率与数据驱动方法处理模型失配、非线性的能力相结合，为复杂动态系统的实时状态估计提供了一种高性能、高鲁棒性的解决方案。

五、总结与思考

5.1 论文主要贡献总结

本文精读的论文《KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics》针对动态系统状态估计中普遍存在的非线性和模型不确定性挑战，提出了一种创新的混合模型驱动（MB）/数据驱动（DD）解决方案——KalmanNet。其核心贡献可总结如下：

1. 新颖的混合架构：KalmanNet创造性地将经典卡尔曼滤波（特别是EKF）的递归结构与深度学习（紧凑型RNN）相结合。它保留并充分利用了部分已知的领域知识（状态转移函数$f$和观测函数$h$，即使近似），同时利用RNN学习并替代了传统滤波流程中最依赖精确噪声统计和易受模型失配影响的环节——卡尔曼增益（KG）的计算。

2. 关键设计要素：

   • 输入特征工程：提出并验证了基于观测和状态估计差值（F1-F4）的特征作为RNN输入，有效捕捉噪声统计和不确定性的关键信息。
   • 两种RNN架构：设计了隐式联合跟踪（架构1，灵活通用）和显式分离跟踪（架构2，参数高效、贴合KF原理）两种RNN实现方案，适应不同需求。
   • 高效的监督训练：采用基于状态估计MSE损失的端到端训练，利用BPTT及其变体（V1-V3）有效处理长时依赖，并证明学习结果具有良好的可迁移性（短训长用）。

3. 显著的性能优势：通过系统性的实验验证，KalmanNet在多种场景下展现出卓越性能：

   • 在线性模型完全信息下达到最优KF的MMSE。
   • 在非线性模型（合成、混沌）和模型失配（参数偏差、传感器失准、连续-离散近似）情况下，性能显著优于主流MB方法（EKF,UKF,PF）和纯粹DD方法（Vanilla RNN）。
   • 在真实世界应用（NCLT里程计定位）中有效抑制传感器漂移，精度远超MBKF。
   • 保持与EKF相当的计算效率，适合嵌入式实时系统。

4. 核心优势融合：KalmanNet成功融合了MB方法的优势（数据效率高、可解释性强、计算高效）和DD方法的优势（处理模型失配、规避噪声建模、克服非线性），为部分已知动态系统的实时状态估计提供了强大且实用的工具。

5.2 技术路线意义与启示

KalmanNet的技术路线对现代信号处理，特别是状态估计领域，具有重要的启示意义：

1. “保留已知，学习未知”的范式：它展示了一种强大的混合系统设计范式——最大程度地保留和利用已有的物理模型/结构化知识作为算法骨架，仅对模型中不确定性强、难以建模或计算的关键环节进行数据驱动的学习替代。这种范式既避免了纯MB方法对模型完备性的苛刻要求，又克服了纯DD方法的数据饥渴、黑盒性和难以利用先验知识的缺点，为处理复杂系统的不确定性问题提供了新思路。

2. 可解释性DD：通过将DNN（RNN）深度集成到一个具有明确物理意义的MB框架（KF流程）中，并让其承担一个特定功能（KG计算），KalmanNet显著提升了DD组件的可解释性。输入特征（新息、状态更新差）、输出（KG）和整个流程都易于理解。这种“白盒化”或“灰盒化”的DD融合策略对于在安全关键领域（如自动驾驶、航空）推广应用至关重要。

3. 聚焦计算瓶颈：识别出KG计算（涉及矩阵求逆和二阶矩传播）是传统KF/EKF中对噪声敏感、易受失配影响、且计算可能不稳定的关键环节，并用学习模块替代，是KalmanNet高效且有效的重要原因。这启示我们在改进传统算法时，应精准定位其性能瓶颈和脆弱点进行智能化增强。

4. 轻量化与实时性：KalmanNet的设计始终考虑计算效率，其紧凑的RNN模块和保留的递归结构确保了其在资源受限设备上的部署可行性（论文在赛车控制单元上的应用即是例证）。这为将AI赋能的高性能算法落地到边缘计算和实时系统提供了范例。

5.3 应用前景与未来方向

应用前景

KalmanNet为解决实际工程中的状态估计难题提供了有力工具，具有广阔的应用前景：

1. 自动驾驶与机器人导航：定位（GPS/INS/里程计融合）、姿态估计、目标跟踪。其对传感器失配和运动模型不确定性的鲁棒性尤其有价值。
2. 工业监测与故障诊断：旋转机械振动状态跟踪、过程工业参数估计。可处理设备退化导致的模型渐变和非线性。
3. 生物医学信号处理：脑电/心电/神经信号中的隐藏状态或特征提取。适应生物系统的个体差异和非线性。
4. 通信与雷达系统：信道估计、目标跟踪、信号滤波。在复杂时变环境中提供鲁棒估计。
5. 金融与经济预测：隐含状态变量（如市场情绪、潜在风险）估计。

未来研究方向

基于KalmanNet的框架，未来研究可以从多个方向深入和扩展：

1. 学习未知模型部分：扩展KalmanNet，使其能够同时利用数据学习部分未知的$f$或$h$（例如用DNN表示），并进行端到端训练，以处理完全或大部分未知解析模型的系统。
2. 不确定性量化：探索如何基于学习到的KG或其他网络输出，提供状态估计的不确定性度量（如置信区间、协方差估计），这对于风险敏感的决策至关重要。
3. 无监督/自监督学习：利用KalmanNet内部产生的预测观测${\hat{y}}_{k|k-1}$进行无监督学习（例如基于预测误差），或者实现在线自适应以跟踪系统动态的缓慢变化。
4. 扩展到其他任务：将KalmanNet的核心思想（混合架构+学习关键环节）扩展到平滑、预测、参数估计等其他状态空间相关的任务。
5. 理论分析：深入研究KalmanNet的收敛性、稳定性、泛化误差界等理论性质，为其可靠性提供更坚实的数学基础。
6. 架构与训练优化：探索更高效的RNN架构（如Transformer元素）、更鲁棒的训练策略、自动化特征选择或架构搜索。
7. 多模态/异构传感器融合：扩展框架以更有效地融合来自不同类型、不同频率、不同可靠性的多源传感器信息。

5.4 个人思考与体会

精读KalmanNet这篇论文，给我带来了深刻的启发和思考：

1. 融合是大势所趋：KalmanNet是模型驱动与数据驱动融合（Model-Based Deep Learning）的典范之作。它清晰地表明，在解决复杂现实世界问题时，纯粹依赖物理模型或纯粹依赖数据都非最优解。未来信号处理算法的突破点，很可能在于如何更智能、更紧耦合地融合这两大范式，做到“知其然（数据），亦知其所以然（模型）”。这种融合不是简单的拼接，而是需要深入理解问题本质，识别各自的优势边界和瓶颈，进行精巧的设计。

2. 可解释性的价值：KalmanNet对可解释性的重视令人印象深刻。在AI日益普及的今天，很多高性能DNN模型因其“黑盒”特性而难以获得信任，特别是在安全攸关领域。KalmanNet通过将其DD组件（RNN）嵌入到具有清晰物理意义的MB框架中，并赋予其明确的功能定位（学习KG），大大提升了系统的透明度和可信度。这提醒我们，在设计智能信号处理系统时，不能只追求性能指标，还需考虑其可解释性和可验证性。

3. 问题驱动的创新：KalmanNet的诞生源于对传统卡尔曼滤波在实际应用（非线性、模型失配）中痛点的深刻洞察。它不是为用AI而用AI，而是针对具体问题（KG计算对噪声和失配敏感）提出的精准解决方案。这体现了以问题为导向、以需求为牵引的科研方法论的重要性。最优秀的创新往往源于对实际挑战的深刻理解和精准把握。

4. 工程落地的考量：论文不仅在理论上创新，还非常注重工程实用性（计算效率、实时性、在嵌入式平台部署）。KalmanNet的轻量化设计和效率保障是其能应用于真实场景（如自动驾驶赛车）的关键。这启示我们，信号处理算法的研究，尤其是结合AI的，必须将落地应用的需求（实时性、资源消耗）贯穿始终。

5. 对自身研究的启示：作为一名现代信号处理的学习者和研究者，KalmanNet为我提供了宝贵的范例。它激励我在未来的研究中：

   • 更加关注实际问题和现有方法的局限性。
   • 积极探索模型与数据融合的创新路径，思考如何在具体任务中识别“已知”与“未知”，设计有针对性的混合架构。
   • 重视算法的可解释性和可部署性。
   • 注重严谨的实验验证，覆盖多种场景（仿真、真实数据）和对比基线。

特别是在研究中需要注意的两个方面：

• 一是研究要找到真问题，这篇论文针对的是卡尔曼滤波状态更新环节中噪声方差模型未知的实际应用限制，核心是如何增强卡尔曼滤波技术的可用性；
• 二是要着眼所研究问题中信息的蕴含方式与技术工具的内在契合性，这篇论文针对状态更新模型未知的困难，利用了深度学习模型在构建映射关系方面的优势，采用模型驱动方式设计整体的处理流程，把神经网络融入其中、化为己用，对问题的理解在整个过程中始终占据主导，而不是被技术工具支配。

该论文所反映的课题研究中需要注意的最关键的两个方面，是我将来研究工作中需要学习借鉴的。

总之，KalmanNet不仅是一项杰出的技术贡献，更是一个展示如何将经典信号处理智慧与现代人工智能技术有效结合的成功案例，为现代信号处理在智能化时代的发展指明了有价值的探索方向。

参考文献

[1] G. Revach, N. Shlezinger, X. Ni, A. López Escoriza, R. J. G. van Sloun, and Y. C. Eldar, “KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics,” IEEE Trans. Signal Process., vol. 70, pp. 1522-1547, 2022. doi: 10.1109/TSP.2022.3158588.
[2] J. Durbin and S. J. Koopman, Time Series Analysis by State Space Methods. Oxford Univ. Press, 2012.
[3] R. E. Kalman, “A new approach to linear filtering and prediction problems,” J. Basic Eng., vol. 82, no. 1, pp. 35–45, 1960.
[4] R. E. Kalman and R. S. Bucy, “New results in linear filtering and prediction theory,” J. Basic Eng., vol. 83, no. 1, pp. 95–108, Mar. 1961.
[5] R. E. Kalman, “New methods in Wiener filtering theory,” in Proc. First Symp. Eng. Appl. Rand. Funct. Theory Prob., Wiley, 1963.
[6] N. Wiener, Extrapolation, Interpolation, and Smoothing of Stationary Time Series: With Engineering Applications, MIT Press, 1949 (vol. 8 of the series).
[7] M. Gruber, “An approach to target tracking,” MIT Lincoln Lab, Tech. Rep. AD0654272, Feb. 1967.
[8] R. E. Larson, R. M. Dressler, and R. S. Ratner, “Application of the extended Kalman filter to ballistic trajectory estimation,” Stanford Res. Inst., Tech. Rep. AD0815377, Jan. 1967.
[9] J. D. McLean, S. F. Schmidt, and L. A. McGee, Optimal Filtering and Linear Prediction Applied to a Midcourse Navigation System for the Circumlunar Mission, NASA Tech. Rep. AD0273085, Mar. 1962.
[10] S. J. Julier and J. K. Uhlmann, “New extension of the Kalman filter to nonlinear systems,” in Proc. SPIE, vol. 3068, 1997, pp. 182–193.
[11] N. J. Gordon, D. J. Salmond, and A. P. Smith, “Novel approach to nonlinear/non-Gaussian Bayesian state estimation,” IEE Proc. F (Radar Signal Process.), vol. 140, no. 2, pp. 107–113, 1993.
[12] P. Del Moral, “Nonlinear filtering: Interacting particle resolution,” C. R. Acad. Sci. Paris Sér. I Math., vol. 325, no. 6, pp. 653–658, 1997.
[13] J. S. Liu and R. Chen, “Sequential Monte Carlo methods for dynamic systems,” J. Amer. Stat. Assoc., vol. 93, no. 443, pp. 1032–1044, 1998.
[14] F. Auger et al., “Industrial applications of the Kalman filter: A review,” IEEE Trans. Ind. Electron., vol. 60, no. 12, pp. 5458–5471, Dec. 2013.
[15] M. Zorzi, “Robust Kalman filtering under model perturbations,” IEEE Trans. Autom. Control, vol. 62, no. 6, pp. 2902–2907, Jun. 2017.
[16] M. Zorzi, “On the robustness of the Bayes and Wiener estimators under model uncertainty,” Automatica, vol. 83, pp. 133–140, 2017.
[17] A. Longhini et al., “Learning the tuned liquid damper dynamics by means of a robust EKF,” in Proc. Amer. Control Conf., 2021, pp. 60–65.
[18] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015.
[19] Y. Bengio, “Learning deep architectures for AI,” Found. Trends Mach. Learn., vol. 2, no. 1, pp. 1–127, 2009.
[20] S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Comput., vol. 9, no. 8, pp. 1735–1780, 1997.
[21] J. Chung, C. Gulcehre, K. Cho, and Y. Bengio, “Empirical evaluation of gated recurrent neural networks on sequence modeling,” arXiv:1412.3555, 2014.
[22] A. Vaswani et al., “Attention is all you need,” in Adv. Neural Inf. Process. Syst., vol. 30, 2017.
[23] M. Zaheer, A. Ahmed, and A. J. Smola, “Latent LSTM allocation: Joint clustering and non-linear dynamic modeling of sequence data,” in Proc. ICML, 2017, pp. 3967–3976.
[24] N. Shlezinger, N. Farsad, Y. C. Eldar, and A. J. Goldsmith, “ViterbiNet: A deep learning based viterbi algorithm for symbol detection,” IEEE Trans. Wireless Commun., vol. 19, no. 5, pp. 3319–3331, May 2020.
[25] N. Shlezinger, R. Fu, and Y. C. Eldar, “DeepsIC: Deep soft interference cancellation for multiuser MIMO detection,” IEEE Trans. Wireless Commun., vol. 20, no. 2, pp. 1349–1362, Feb. 2021.
[26] N. Shlezinger, N. Farsad, Y. C. Eldar, and A. J. Goldsmith, “Learned factor graphs for inference from stationary time sequences,” IEEE Trans. Signal Process., vol. 70, pp. 366–380, 2022.
[27] N. Shlezinger, J. Whang, Y. C. Eldar, and A. G. Dimakis, “Model-based deep learning,” arXiv:2012.08405, 2020.
[28] N. Carlevaris-Bianco, A. K. Ushani, and R. M. Eustice, “University of Michigan north campus long-term vision and LiDAR dataset,” Int. J. Robot. Res., vol. 35, no. 9, pp. 1023–1035, 2016.
[29] R. G. Krishnan, U. Shalit, and D. Sontag, “Deep Kalman filters,” arXiv:1511.05121, 2015.
[30] M. Karl, M. Soelch, J. Bayer, and P. van der Smagt, “Deep variational Bayes filters: Unsupervised learning of state space models from raw data,” arXiv:1605.06432, 2016.
[31] M. Fraccaro, S. K. Sønderby, U. Paquet, and O. Winther, “A disentangled recognition and nonlinear dynamics model for unsupervised learning,” in Adv. Neural Inf. Process. Syst., vol. 30, 2017.
[32] C. Naesseth, S. Linderman, R. Ranganath, and D. Blei, “Variational sequential Monte Carlo,” in Proc. AISTATS, 2018, pp. 968–977.
[33] E. Archer et al., “Black box variational inference for state space models,” arXiv:1511.07367, 2015.
[34] R. Krishnan, U. Shalit, and D. Sontag, “Structured inference networks for nonlinear state space models,” in Proc. AAAI, vol. 31, no. 1, 2017.
[35] V. G. Satorras, Z. Akata, and M. Welling, “Combining generative and discriminative models for hybrid inference,” in Adv. Neural Inf. Process. Syst., vol. 32, 2019.
[36] Y. Bar-Shalom, X. R. Li, and T. Kirubarajan, Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software. Wiley, 2004.
[37] K.-V. Yuen and S.-C. Kuok, “Online updating and uncertainty quantification using nonstationary output-only measurement,” Mech. Syst. Signal Process., vol. 66, pp. 62–77, 2016.
[38] H.-Q. Mu, S.-C. Kuok, and K.-V. Yuen, “Stable robust extended Kalman filter,” J. Aerosp. Eng., vol. 30, no. 3, 2017, Art. no. B4016010.
[39] I. Arasaratnam, S. Haykin, and R. J. Elliott, “Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature,” Proc. IEEE, vol. 95, no. 5, pp. 953–977, May 2007.
[40] I. Arasaratnam and S. Haykin, “Cubature Kalman filters,” IEEE Trans. Autom. Control, vol. 54, no. 6, pp. 1254–1269, Jun. 2009.
[41] M. S. Arulampalam et al., “A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking,” IEEE Trans. Signal Process., vol. 50, no. 2, pp. 174–188, Feb. 2002.
[42] N. Chopin, P. E. Jacob, and O. Papaspiliopoulos, “SMC2: An efficient algorithm for sequential analysis of state space models,” J. R. Stat. Soc. B, vol. 75, no. 3, pp. 397–426, 2013.
[43] L. Martino, V. Elvira, and G. Camps-Valls, “Distributed particle Metropolis-Hastings schemes,” in Proc. IEEE SSP Workshop, 2018, pp. 553–557.
[44] C. Andrieu, A. Doucet, and R. Holenstein, “Particle Markov chain Monte Carlo methods,” J. R. Stat. Soc. B, vol. 72, no. 3, pp. 269–342, 2010.
[45] J. Elfring, E. Torta, and R. van de Molengraft, “Particle filters: A hands-on tutorial,” Sensors, vol. 21, no. 2, p. 438, 2021.
[46] R. H. Shumway and D. S. Stoffer, “An approach to time series smoothing and forecasting using the EM algorithm,” J. Time Ser. Anal., vol. 3, no. 4, pp. 253–264, 1982.
[47] Z. Ghahramani and G. E. Hinton, “Parameter estimation for linear dynamical systems,” Univ. Toronto, Tech. Rep. CRG-TR-96-2, 1996.
[48] J. Dauwels, A. Eckford, S. Korl, and H.-A. Loeliger, “Expectation maximization as message passing,” arXiv:0910.2832, 2009.
[49] L. Martino, J. Read, V. Elvira, and F. Louzada, “Cooperative parallel particle filters for online model selection and applications to urban mobility,” Digit. Signal Process., vol. 60, pp. 172–185, 2017.
[50] P. Abbeel et al., “Discriminative training of Kalman filters,” in Proc. Robot.: Sci. Syst., 2005.
[51] L. Xu and R. Niu, “EKFNet: Learning system noise statistics from measurement data,” in Proc. IEEE ICASSP, 2021, pp. 4560–4564.
[52] S. T. Barratt and S. P. Boyd, “Fitting a Kalman smoother to data,” in Proc. Amer. Control Conf., 2020, pp. 1526–1531.
[53] L. Xie, Y. C. Soh, and C. E. de Souza, “Robust Kalman filtering for uncertain discrete-time systems,” IEEE Trans. Autom. Control, vol. 39, no. 6, pp. 1310–1314, Jun. 1994.
[54] C. M. Carvalho et al., “Particle learning and smoothing,” Stat. Sci., vol. 25, no. 1, pp. 88–106, 2010.
[55] I. Urteaga, M. F. Bugallo, and P. M. Djuric, “Sequential Monte Carlo methods under model uncertainty,” in Proc. IEEE SSP Workshop, 2016, pp. 1–5.
[56] L. Zhou et al., “KFNet: Learning temporal camera relocalization using Kalman filtering,” in Proc. IEEE/CVF CVPR, 2020, pp. 4919–4928.
[57] D. P. Kingma and M. Welling, “Auto-encoding variational Bayes,” arXiv:1312.6114, 2013.
[58] D. J. Rezende, S. Mohamed, and D. Wierstra, “Stochastic backpropagation and approximate inference in deep generative models,” in Proc. ICML, 2014, pp. 1278–1286.
[59] D. M. Blei, A. Kucukelbir, and J. D. McAuliffe, “Variational inference: A review for statisticians,” J. Amer. Stat. Assoc., vol. 112, no. 518, pp. 859–877, 2017.
[60] T. Haarnoja, A. Ajay, S. Levine, and P. Abbeel, “Backprop KF: Learning discriminative deterministic state estimators,” in Adv. Neural Inf. Process. Syst., vol. 29, 2016.
[61] B. Laufer-Goldshtein, R. Talmon, and S. Gannot, “A hybrid approach for speaker tracking based on TDOA and data-driven models,” IEEE/ACM Trans. Audio, Speech, Lang. Process., vol. 26, no. 4, pp. 725–735, Apr. 2018.
[62] H. Coskun et al., “Long short-term memory Kalman filters: Recurrent neural estimators for pose regularization,” in Proc. IEEE ICCV, 2017, pp. 5524–5532.
[63] S. S. Rangapuram et al., “Deep state space models for time series forecasting,” in Adv. Neural Inf. Process. Syst., vol. 31, 2018.
[64] P. Becker et al., “Recurrent Kalman networks: Factorized inference in high-dimensional deep feature spaces,” in Proc. ICML, 2019, pp. 544–552.
[65] X. Zheng et al., “State space LSTM models with particle MCMC inference,” OpenReview, 2018.
[66] T. Salimans, D. Kingma, and M. Welling, “Markov chain Monte Carlo and variational inference: Bridging the gap,” in Proc. ICML, 2015, pp. 1218–1226.
[67] X. Ni, G. Revach, N. Shlezinger, R. J. van Sloun, and Y. C. Eldar, “RTSNET: Deep learning aided Kalman smoothing,” in Proc. IEEE ICASSP, 2022.
[68] R. Dey and F. M. Salem, “Gate-variants of gated recurrent unit (GRU) neural networks,” in Proc. IEEE MWSCAS, 2017, pp. 1597–1600.
[69] P. J. Werbos, “Backpropagation through time: What it does and how to do it,” Proc. IEEE, vol. 78, no. 10, pp. 1550–1560, Oct. 1990.
[70] I. Sutskever, Training Recurrent Neural Networks, Ph.D. dissertation, Univ. Toronto, 2013.
[71] I. Klein, G. Revach, N. Shlezinger, J. E. Mehr, R. J. van Sloun, and Y. Eldar, “Uncertainty in data-driven Kalman filtering for partially known state-space models,” in Proc. IEEE ICASSP, 2022.
[72] A. Lopez Escoriza, G. Revach, N. Shlezinger, and R. J. G. van Sloun, “Data-driven Kalman-based velocity estimation for autonomous racing,” in Proc. IEEE ICAS, 2021, pp. 1–5.
[73] H. E. Rauch, F. Tung, and C. T. Striebel, “Maximum likelihood estimates of linear dynamic systems,” AIAA J., vol. 3, no. 8, pp. 1445–1450, 1965.
[74] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv:1412.6980, 2014.
[75] R. Labbe, “FilterPy - Kalman and Bayesian filters in Python,” [Online]. Available: https://filterpy.readthedocs.io/
[76] J. Nordh, “pyParticleEst - particle based methods in python,” [Online]. Available: https://pyparticleest.readthedocs.io/
[77] W. Gilpin, “Chaos as an interpretable benchmark for forecasting and data-driven modelling,” in NeurIPS Datasets Benchmarks Track, 2021.

KalmanNet及相关滤波算法代码整理

1. KalmanNet核心网络代码

"""# **Class: KalmanNet**"""import torch
import torch.nn as nn
import torch.nn.functional as funcclass KalmanNetNN(torch.nn.Module):###################### Constructor ######################def __init__(self):super().__init__()def NNBuild(self, SysModel, args):# Deviceif args.use_cuda:self.device = torch.device('cuda')else:self.device = torch.device('cpu')self.InitSystemDynamics(SysModel.f, SysModel.h, SysModel.m, SysModel.n)# Number of neurons in the 1st hidden layer#H1_KNet = (SysModel.m + SysModel.n) * (10) * 8# Number of neurons in the 2nd hidden layer#H2_KNet = (SysModel.m * SysModel.n) * 1 * (4)self.InitKGainNet(SysModel.prior_Q, SysModel.prior_Sigma, SysModel.prior_S, args)######################################### Initialize Kalman Gain Network #########################################def InitKGainNet(self, prior_Q, prior_Sigma, prior_S, args):self.seq_len_input = 1 # KNet calculates time-step by time-stepself.batch_size = args.n_batch # Batch sizeself.prior_Q = prior_Q.to(self.device)self.prior_Sigma = prior_Sigma.to(self.device)self.prior_S = prior_S.to(self.device)# GRU to track Qself.d_input_Q = self.m * args.in_mult_KNetself.d_hidden_Q = self.m ** 2self.GRU_Q = nn.GRU(self.d_input_Q, self.d_hidden_Q).to(self.device)# GRU to track Sigmaself.d_input_Sigma = self.d_hidden_Q + self.m * args.in_mult_KNetself.d_hidden_Sigma = self.m ** 2self.GRU_Sigma = nn.GRU(self.d_input_Sigma, self.d_hidden_Sigma).to(self.device)# GRU to track Sself.d_input_S = self.n ** 2 + 2 * self.n * args.in_mult_KNetself.d_hidden_S = self.n ** 2self.GRU_S = nn.GRU(self.d_input_S, self.d_hidden_S).to(self.device)# Fully connected 1self.d_input_FC1 = self.d_hidden_Sigmaself.d_output_FC1 = self.n ** 2self.FC1 = nn.Sequential(nn.Linear(self.d_input_FC1, self.d_output_FC1),nn.ReLU()).to(self.device)# Fully connected 2self.d_input_FC2 = self.d_hidden_S + self.d_hidden_Sigmaself.d_output_FC2 = self.n * self.mself.d_hidden_FC2 = self.d_input_FC2 * args.out_mult_KNetself.FC2 = nn.Sequential(nn.Linear(self.d_input_FC2, self.d_hidden_FC2),nn.ReLU(),nn.Linear(self.d_hidden_FC2, self.d_output_FC2)).to(self.device)# Fully connected 3self.d_input_FC3 = self.d_hidden_S + self.d_output_FC2self.d_output_FC3 = self.m ** 2self.FC3 = nn.Sequential(nn.Linear(self.d_input_FC3, self.d_output_FC3),nn.ReLU()).to(self.device)# Fully connected 4self.d_input_FC4 = self.d_hidden_Sigma + self.d_output_FC3self.d_output_FC4 = self.d_hidden_Sigmaself.FC4 = nn.Sequential(nn.Linear(self.d_input_FC4, self.d_output_FC4),nn.ReLU()).to(self.device)# Fully connected 5self.d_input_FC5 = self.mself.d_output_FC5 = self.m * args.in_mult_KNetself.FC5 = nn.Sequential(nn.Linear(self.d_input_FC5, self.d_output_FC5),nn.ReLU()).to(self.device)# Fully connected 6self.d_input_FC6 = self.mself.d_output_FC6 = self.m * args.in_mult_KNetself.FC6 = nn.Sequential(nn.Linear(self.d_input_FC6, self.d_output_FC6),nn.ReLU()).to(self.device)# Fully connected 7self.d_input_FC7 = 2 * self.nself.d_output_FC7 = 2 * self.n * args.in_mult_KNetself.FC7 = nn.Sequential(nn.Linear(self.d_input_FC7, self.d_output_FC7),nn.ReLU()).to(self.device)##################################### Initialize System Dynamics #####################################def InitSystemDynamics(self, f, h, m, n):# Set State Evolution Functionself.f = fself.m = m# Set Observation Functionself.h = hself.n = n############################## Initialize Sequence ##############################def InitSequence(self, M1_0, T):"""input M1_0 (torch.tensor): 1st moment of x at time 0 [batch_size, m, 1]"""self.T = Tself.m1x_posterior = M1_0.to(self.device)self.m1x_posterior_previous = self.m1x_posteriorself.m1x_prior_previous = self.m1x_posteriorself.y_previous = self.h(self.m1x_posterior)######################### Compute Priors #########################def step_prior(self):# Predict the 1-st moment of xself.m1x_prior = self.f(self.m1x_posterior)# Predict the 1-st moment of yself.m1y = self.h(self.m1x_prior)################################# Kalman Gain Estimation #################################def step_KGain_est(self, y):# both in size [batch_size, n]obs_diff = torch.squeeze(y,2) - torch.squeeze(self.y_previous,2) obs_innov_diff = torch.squeeze(y,2) - torch.squeeze(self.m1y,2)# both in size [batch_size, m]fw_evol_diff = torch.squeeze(self.m1x_posterior,2) - torch.squeeze(self.m1x_posterior_previous,2)fw_update_diff = torch.squeeze(self.m1x_posterior,2) - torch.squeeze(self.m1x_prior_previous,2)obs_diff = func.normalize(obs_diff, p=2, dim=1, eps=1e-12, out=None)obs_innov_diff = func.normalize(obs_innov_diff, p=2, dim=1, eps=1e-12, out=None)fw_evol_diff = func.normalize(fw_evol_diff, p=2, dim=1, eps=1e-12, out=None)fw_update_diff = func.normalize(fw_update_diff, p=2, dim=1, eps=1e-12, out=None)# Kalman Gain Network StepKG = self.KGain_step(obs_diff, obs_innov_diff, fw_evol_diff, fw_update_diff)# Reshape Kalman Gain to a Matrixself.KGain = torch.reshape(KG, (self.batch_size, self.m, self.n))########################## Kalman Net Step ##########################def KNet_step(self, y):# Compute Priorsself.step_prior()# Compute Kalman Gainself.step_KGain_est(y)# Innovationdy = y - self.m1y # [batch_size, n, 1]# Compute the 1-st posterior momentINOV = torch.bmm(self.KGain, dy)self.m1x_posterior_previous = self.m1x_posteriorself.m1x_posterior = self.m1x_prior + INOV#self.state_process_posterior_0 = self.state_process_prior_0self.m1x_prior_previous = self.m1x_prior# update y_prevself.y_previous = y# returnreturn self.m1x_posterior########################### Kalman Gain Step ###########################def KGain_step(self, obs_diff, obs_innov_diff, fw_evol_diff, fw_update_diff):def expand_dim(x):expanded = torch.empty(self.seq_len_input, self.batch_size, x.shape[-1]).to(self.device)expanded[0, :, :] = xreturn expandedobs_diff = expand_dim(obs_diff)obs_innov_diff = expand_dim(obs_innov_diff)fw_evol_diff = expand_dim(fw_evol_diff)fw_update_diff = expand_dim(fw_update_diff)####################### Forward Flow ######################## FC 5in_FC5 = fw_update_diffout_FC5 = self.FC5(in_FC5)# Q-GRUin_Q = out_FC5out_Q, self.h_Q = self.GRU_Q(in_Q, self.h_Q)# FC 6in_FC6 = fw_evol_diffout_FC6 = self.FC6(in_FC6)# Sigma_GRUin_Sigma = torch.cat((out_Q, out_FC6), 2)out_Sigma, self.h_Sigma = self.GRU_Sigma(in_Sigma, self.h_Sigma)# FC 1in_FC1 = out_Sigmaout_FC1 = self.FC1(in_FC1)# FC 7in_FC7 = torch.cat((obs_diff, obs_innov_diff), 2)out_FC7 = self.FC7(in_FC7)# S-GRUin_S = torch.cat((out_FC1, out_FC7), 2)out_S, self.h_S = self.GRU_S(in_S, self.h_S)# FC 2in_FC2 = torch.cat((out_Sigma, out_S), 2)out_FC2 = self.FC2(in_FC2)######################## Backward Flow ######################### FC 3in_FC3 = torch.cat((out_S, out_FC2), 2)out_FC3 = self.FC3(in_FC3)# FC 4in_FC4 = torch.cat((out_Sigma, out_FC3), 2)out_FC4 = self.FC4(in_FC4)# updating hidden state of the Sigma-GRUself.h_Sigma = out_FC4return out_FC2################## Forward ##################def forward(self, y):y = y.to(self.device)return self.KNet_step(y)############################ Init Hidden State ############################def init_hidden_KNet(self):weight = next(self.parameters()).datahidden = weight.new(self.seq_len_input, self.batch_size, self.d_hidden_S).zero_()self.h_S = hidden.dataself.h_S = self.prior_S.flatten().reshape(1, 1, -1).repeat(self.seq_len_input,self.batch_size, 1) # batch size expansionhidden = weight.new(self.seq_len_input, self.batch_size, self.d_hidden_Sigma).zero_()self.h_Sigma = hidden.dataself.h_Sigma = self.prior_Sigma.flatten().reshape(1,1,-1).repeat(self.seq_len_input,self.batch_size, 1) # batch size expansionhidden = weight.new(self.seq_len_input, self.batch_size, self.d_hidden_Q).zero_()self.h_Q = hidden.dataself.h_Q = self.prior_Q.flatten().reshape(1,1,-1).repeat(self.seq_len_input,self.batch_size, 1) # batch size expansion

2. 非线性洛伦兹吸引子案例代码

import torch
torch.pi = torch.acos(torch.zeros(1)).item() * 2 # which is 3.1415927410125732
import torch.nn as nn
from Filters.EKF_test import EKFTestfrom Simulations.Extended_sysmdl import SystemModel
from Simulations.utils import DataGen,Short_Traj_Split
import Simulations.config as configfrom Pipelines.Pipeline_EKF import Pipeline_EKFfrom datetime import datetimefrom KNet.KalmanNet_nn import KalmanNetNNfrom Simulations.Lorenz_Atractor.parameters import m1x_0, m2x_0, m, n,\
f, h, hRotate, H_Rotate, H_Rotate_inv, Q_structure, R_structureprint("Pipeline Start")
################
### Get Time ###
################
today = datetime.today()
now = datetime.now()
strToday = today.strftime("%m.%d.%y")
strNow = now.strftime("%H:%M:%S")
strTime = strToday + "_" + strNow
print("Current Time =", strTime)###################
###  Settings   ###
###################
args = config.general_settings()
### dataset parameters
args.N_E = 1000
args.N_CV = 100
args.N_T = 200
args.T = 100
args.T_test = 100
### training parameters
args.use_cuda = True # use GPU or not
args.n_steps = 2000
args.n_batch = 30
args.lr = 1e-3
args.wd = 1e-3if args.use_cuda:if torch.cuda.is_available():device = torch.device('cuda')print("Using GPU")else:raise Exception("No GPU found, please set args.use_cuda = False")
else:device = torch.device('cpu')print("Using CPU")
device = torch.device('cpu')
offset = 0 # offset for the data
chop = False # whether to chop data sequences into shorter sequences
path_results = 'KNet/'
DatafolderName = 'Simulations/Lorenz_Atractor/data' + '/'
switch = 'partial' # 'full' or 'partial' or 'estH'# noise q and r
r2 = torch.tensor([0.1]) # [100, 10, 1, 0.1, 0.01]
vdB = -20 # ratio v=q2/r2
v = 10**(vdB/10)
q2 = torch.mul(v,r2)Q = q2[0] * Q_structure
R = r2[0] * R_structureprint("1/r2 [dB]: ", 10 * torch.log10(1/r2[0]))
print("1/q2 [dB]: ", 10 * torch.log10(1/q2[0]))traj_resultName = ['traj_lorDT_rq1030_T100.pt']
dataFileName = ['data_lor_v20_rq1030_T100.pt']#########################################
###  Generate and load data DT case   ###
#########################################sys_model = SystemModel(f, Q, hRotate, R, args.T, args.T_test, m, n)# parameters for GT
sys_model.InitSequence(m1x_0, m2x_0)# x0 and P0print("Start Data Gen")
DataGen(args, sys_model, DatafolderName + dataFileName[0])
print("Data Load")
print(dataFileName[0])
[train_input_long,train_target_long, cv_input, cv_target, test_input, test_target,_,_,_] =  torch.load(DatafolderName + dataFileName[0], map_location=device)  
if chop: print("chop training data")    [train_target, train_input, train_init] = Short_Traj_Split(train_target_long, train_input_long, args.T)# [cv_target, cv_input] = Short_Traj_Split(cv_target, cv_input, args.T)
else:print("no chopping") train_target = train_target_long[:,:,0:args.T]train_input = train_input_long[:,:,0:args.T] # cv_target = cv_target[:,:,0:args.T]# cv_input = cv_input[:,:,0:args.T]  print("trainset size:",train_target.size())
print("cvset size:",cv_target.size())
print("testset size:",test_target.size())# Model with partial info
sys_model_partial = SystemModel(f, Q, h, R, args.T, args.T_test, m, n)
sys_model_partial.InitSequence(m1x_0, m2x_0)
# Model for 2nd pass
sys_model_pass2 = SystemModel(f, Q, h, R, args.T, args.T_test, m, n)# parameters for GT
sys_model_pass2.InitSequence(m1x_0, m2x_0)# x0 and P0########################################
### Evaluate Observation Noise Floor ###
########################################
N_T = len(test_input)
loss_obs = nn.MSELoss(reduction='mean')
MSE_obs_linear_arr = torch.empty(N_T)# MSE [Linear]for j in range(0, N_T): reversed_target = torch.matmul(H_Rotate_inv, test_input[j])      MSE_obs_linear_arr[j] = loss_obs(reversed_target, test_target[j]).item()
MSE_obs_linear_avg = torch.mean(MSE_obs_linear_arr)
MSE_obs_dB_avg = 10 * torch.log10(MSE_obs_linear_avg)# Standard deviation
MSE_obs_linear_std = torch.std(MSE_obs_linear_arr, unbiased=True)# Confidence interval
obs_std_dB = 10 * torch.log10(MSE_obs_linear_std + MSE_obs_linear_avg) - MSE_obs_dB_avgprint("Observation Noise Floor(test dataset) - MSE LOSS:", MSE_obs_dB_avg, "[dB]")
print("Observation Noise Floor(test dataset) - STD:", obs_std_dB, "[dB]")########################
### Evaluate Filters ###
########################
### Evaluate EKF true
# print("Evaluate EKF true")
# [MSE_EKF_linear_arr, MSE_EKF_linear_avg, MSE_EKF_dB_avg, EKF_KG_array, EKF_out] = EKFTest(args, sys_model, test_input, test_target)
# ### Evaluate EKF partial
# print("Evaluate EKF partial")
# [MSE_EKF_linear_arr_partial, MSE_EKF_linear_avg_partial, MSE_EKF_dB_avg_partial, EKF_KG_array_partial, EKF_out_partial] = EKFTest(args, sys_model_partial, test_input, test_target)# ### Save trajectories
# trajfolderName = 'Filters' + '/'
# DataResultName = traj_resultName[0]
# EKF_sample = torch.reshape(EKF_out[0],[1,m,args.T_test])
# target_sample = torch.reshape(test_target[0,:,:],[1,m,args.T_test])
# input_sample = torch.reshape(test_input[0,:,:],[1,n,args.T_test])
# torch.save({
#             'EKF': EKF_sample,
#             'ground_truth': target_sample,
#             'observation': input_sample,
#             }, trajfolderName+DataResultName)#####################
### Evaluate KNet ###
#####################
if switch == 'full':## KNet with full info ###################################################################################################### KNet full ###################  ## Build Neural Networkprint("KNet with full model info")KNet_model = KalmanNetNN()KNet_model.NNBuild(sys_model, args)# ## Train Neural NetworkKNet_Pipeline = Pipeline_EKF(strTime, "KNet", "KNet")KNet_Pipeline.setssModel(sys_model)KNet_Pipeline.setModel(KNet_model)print("Number of trainable parameters for KNet:",sum(p.numel() for p in KNet_model.parameters() if p.requires_grad))KNet_Pipeline.setTrainingParams(args) if(chop):[MSE_cv_linear_epoch, MSE_cv_dB_epoch, MSE_train_linear_epoch, MSE_train_dB_epoch] = KNet_Pipeline.NNTrain(sys_model, cv_input, cv_target, train_input, train_target, path_results, randomInit=True, train_init=train_init)else:[MSE_cv_linear_epoch, MSE_cv_dB_epoch, MSE_train_linear_epoch, MSE_train_dB_epoch] = KNet_Pipeline.NNTrain(sys_model, cv_input, cv_target, train_input, train_target, path_results)## Test Neural Network[MSE_test_linear_arr, MSE_test_linear_avg, MSE_test_dB_avg,Knet_out,RunTime] = KNet_Pipeline.NNTest(sys_model, test_input, test_target, path_results)####################################################################################
elif switch == 'partial':## KNet with model mismatch ######################################################################################################### KNet partial ######################### Build Neural Networkprint("KNet with observation model mismatch")KNet_model = KalmanNetNN()KNet_model.NNBuild(sys_model_partial, args)## Train Neural NetworkKNet_Pipeline = Pipeline_EKF(strTime, "KNet", "KNet")KNet_Pipeline.setssModel(sys_model_partial)KNet_Pipeline.setModel(KNet_model)KNet_Pipeline.setTrainingParams(args)if(chop):[MSE_cv_linear_epoch, MSE_cv_dB_epoch, MSE_train_linear_epoch, MSE_train_dB_epoch] = KNet_Pipeline.NNTrain(sys_model_partial, cv_input, cv_target, train_input, train_target, path_results, randomInit=True, train_init=train_init)else:[MSE_cv_linear_epoch, MSE_cv_dB_epoch, MSE_train_linear_epoch, MSE_train_dB_epoch] = KNet_Pipeline.NNTrain(sys_model_partial, cv_input, cv_target, train_input, train_target, path_results)## Test Neural Network[MSE_test_linear_arr, MSE_test_linear_avg, MSE_test_dB_avg,Knet_out,RunTime] = KNet_Pipeline.NNTest(sys_model_partial, test_input, test_target, path_results)###################################################################################
elif switch == 'estH':print("True Observation matrix H:", H_Rotate)### Least square estimation of HX = torch.squeeze(train_target[:,:,0])Y = torch.squeeze(train_input[:,:,0])for t in range(1,args.T):X_t = torch.squeeze(train_target[:,:,t])Y_t = torch.squeeze(train_input[:,:,t])X = torch.cat((X,X_t),0)Y = torch.cat((Y,Y_t),0)Y_1 = torch.unsqueeze(Y[:,0],1)Y_2 = torch.unsqueeze(Y[:,1],1)Y_3 = torch.unsqueeze(Y[:,2],1)H_row1 = torch.matmul(torch.matmul(torch.inverse(torch.matmul(X.T,X)),X.T),Y_1)H_row2 = torch.matmul(torch.matmul(torch.inverse(torch.matmul(X.T,X)),X.T),Y_2)H_row3 = torch.matmul(torch.matmul(torch.inverse(torch.matmul(X.T,X)),X.T),Y_3)H_hat = torch.cat((H_row1.T,H_row2.T,H_row3.T),0)print("Estimated Observation matrix H:", H_hat)def h_hat(x, jacobian=False):H = H_hat.reshape((1, n, m)).repeat(x.shape[0], 1, 1) # [batch_size, n, m] y = torch.bmm(H,x)if jacobian:return y, Helse:return y# Estimated modelsys_model_esth = SystemModel(f, Q, h_hat, R, args.T, args.T_test, m, n)sys_model_esth.InitSequence(m1x_0, m2x_0)################## KNet estH ###################print("KNet with estimated H")KNet_Pipeline = Pipeline_EKF(strTime, "KNet", "KNetEstH_"+ dataFileName[0])KNet_Pipeline.setssModel(sys_model_esth)KNet_model = KalmanNetNN()KNet_model.NNBuild(sys_model_esth, args)KNet_Pipeline.setModel(KNet_model)KNet_Pipeline.setTrainingParams(args)[MSE_cv_linear_epoch, MSE_cv_dB_epoch, MSE_train_linear_epoch, MSE_train_dB_epoch] = KNet_Pipeline.NNTrain(sys_model_esth, cv_input, cv_target, train_input, train_target, path_results)## Test Neural Network[MSE_test_linear_arr, MSE_test_linear_avg, MSE_test_dB_avg,Knet_out,RunTime] = KNet_Pipeline.NNTest(sys_model_esth, test_input, test_target, path_results)###################################################################################
else:print("Error in switch! Please try 'full' or 'partial' or 'estH'.")

3. 线性Kalman滤波代码

"""# **Class: Kalman Filter**
Theoretical Linear Kalman Filter
batched version
"""
import torchclass KalmanFilter:def __init__(self, SystemModel, args):# Deviceif args.use_cuda:self.device = torch.device('cuda')else:self.device = torch.device('cpu')self.F = SystemModel.Fself.m = SystemModel.mself.Q = SystemModel.Q.to(self.device)self.H = SystemModel.Hself.n = SystemModel.nself.R = SystemModel.R.to(self.device)self.T = SystemModel.Tself.T_test = SystemModel.T_test# Predictdef Predict(self):# Predict the 1-st moment of xself.m1x_prior = torch.bmm(self.batched_F, self.m1x_posterior).to(self.device)# Predict the 2-nd moment of xself.m2x_prior = torch.bmm(self.batched_F, self.m2x_posterior)self.m2x_prior = torch.bmm(self.m2x_prior, self.batched_F_T) + self.Q# Predict the 1-st moment of yself.m1y = torch.bmm(self.batched_H, self.m1x_prior)# Predict the 2-nd moment of yself.m2y = torch.bmm(self.batched_H, self.m2x_prior)self.m2y = torch.bmm(self.m2y, self.batched_H_T) + self.R# Compute the Kalman Gaindef KGain(self):self.KG = torch.bmm(self.m2x_prior, self.batched_H_T)self.KG = torch.bmm(self.KG, torch.inverse(self.m2y))# Innovationdef Innovation(self, y):self.dy = y - self.m1y# Compute Posteriordef Correct(self):# Compute the 1-st posterior momentself.m1x_posterior = self.m1x_prior + torch.bmm(self.KG, self.dy)# Compute the 2-nd posterior momentself.m2x_posterior = torch.bmm(self.m2y, torch.transpose(self.KG, 1, 2))self.m2x_posterior = self.m2x_prior - torch.bmm(self.KG, self.m2x_posterior)def Update(self, y):self.Predict()self.KGain()self.Innovation(y)self.Correct()return self.m1x_posterior,self.m2x_posteriordef Init_batched_sequence(self, m1x_0_batch, m2x_0_batch):self.m1x_0_batch = m1x_0_batch # [batch_size, m, 1]self.m2x_0_batch = m2x_0_batch # [batch_size, m, m]######################### Generate Batch #########################def GenerateBatch(self, y):"""input y: batch of observations [batch_size, n, T]"""y = y.to(self.device)self.batch_size = y.shape[0] # batch sizeT = y.shape[2] # sequence length (maximum length if randomLength=True)# Batched F and Hself.batched_F = self.F.view(1,self.m,self.m).expand(self.batch_size,-1,-1).to(self.device)self.batched_F_T = torch.transpose(self.batched_F, 1, 2).to(self.device)self.batched_H = self.H.view(1,self.n,self.m).expand(self.batch_size,-1,-1).to(self.device)self.batched_H_T = torch.transpose(self.batched_H, 1, 2).to(self.device)# Allocate Array for 1st and 2nd order moments (use zero padding)self.x = torch.zeros(self.batch_size, self.m, T).to(self.device)self.sigma = torch.zeros(self.batch_size, self.m, self.m, T).to(self.device)# Set 1st and 2nd order moments for t=0self.m1x_posterior = self.m1x_0_batch.to(self.device)self.m2x_posterior = self.m2x_0_batch.to(self.device)# Generate in a batched mannerfor t in range(0, T):yt = torch.unsqueeze(y[:, :, t],2)xt,sigmat = self.Update(yt)self.x[:, :, t] = torch.squeeze(xt,2)self.sigma[:, :, :, t] = sigmat

4. 扩展Kalman滤波代码

"""# **Class: Extended Kalman Filter**
Theoretical Non Linear Kalman
"""
import torchfrom Simulations.Lorenz_Atractor.parameters import getJacobianclass ExtendedKalmanFilter:def __init__(self, SystemModel, args):# Deviceif args.use_cuda:self.device = torch.device('cuda')else:self.device = torch.device('cpu')# process modelself.f = SystemModel.fself.m = SystemModel.mself.Q = SystemModel.Q.to(self.device)# observation modelself.h = SystemModel.hself.n = SystemModel.nself.R = SystemModel.R.to(self.device)# sequence length (use maximum length if random length case)self.T = SystemModel.Tself.T_test = SystemModel.T_test# Predictdef Predict(self):# Predict the 1-st moment of xself.m1x_prior = self.f(self.m1x_posterior).to(self.device)# Compute the Jacobiansself.UpdateJacobians(getJacobian(self.m1x_posterior,self.f), getJacobian(self.m1x_prior, self.h))# Predict the 2-nd moment of xself.m2x_prior = torch.bmm(self.batched_F, self.m2x_posterior)self.m2x_prior = torch.bmm(self.m2x_prior, self.batched_F_T) + self.Q# Predict the 1-st moment of yself.m1y = self.h(self.m1x_prior)# Predict the 2-nd moment of yself.m2y = torch.bmm(self.batched_H, self.m2x_prior)self.m2y = torch.bmm(self.m2y, self.batched_H_T) + self.R# Compute the Kalman Gaindef KGain(self):self.KG = torch.bmm(self.m2x_prior, self.batched_H_T)self.KG = torch.bmm(self.KG, torch.inverse(self.m2y))#Save KalmanGainself.KG_array[:,:,:,self.i] = self.KGself.i += 1# Innovationdef Innovation(self, y):self.dy = y - self.m1y# Compute Posteriordef Correct(self):# Compute the 1-st posterior momentself.m1x_posterior = self.m1x_prior + torch.bmm(self.KG, self.dy)# Compute the 2-nd posterior momentself.m2x_posterior = torch.bmm(self.m2y, torch.transpose(self.KG, 1, 2))self.m2x_posterior = self.m2x_prior - torch.bmm(self.KG, self.m2x_posterior)def Update(self, y):self.Predict()self.KGain()self.Innovation(y)self.Correct()return self.m1x_posterior, self.m2x_posterior#########################def UpdateJacobians(self, F, H):self.batched_F = F.to(self.device)self.batched_F_T = torch.transpose(F,1,2)self.batched_H = H.to(self.device)self.batched_H_T = torch.transpose(H,1,2)def Init_batched_sequence(self, m1x_0_batch, m2x_0_batch):self.m1x_0_batch = m1x_0_batch # [batch_size, m, 1]self.m2x_0_batch = m2x_0_batch # [batch_size, m, m]######################### Generate Batch #########################def GenerateBatch(self, y):"""input y: batch of observations [batch_size, n, T]"""y = y.to(self.device)self.batch_size = y.shape[0] # batch sizeT = y.shape[2] # sequence length (maximum length if randomLength=True)# Pre allocate KG arrayself.KG_array = torch.zeros([self.batch_size,self.m,self.n,T]).to(self.device)self.i = 0 # Index for KG_array alocation# Allocate Array for 1st and 2nd order moments (use zero padding)self.x = torch.zeros(self.batch_size, self.m, T).to(self.device)self.sigma = torch.zeros(self.batch_size, self.m, self.m, T).to(self.device)# Set 1st and 2nd order moments for t=0self.m1x_posterior = self.m1x_0_batch.to(self.device)self.m2x_posterior = self.m2x_0_batch.to(self.device)# Generate in a batched mannerfor t in range(0, T):yt = torch.unsqueeze(y[:, :, t],2)xt,sigmat = self.Update(yt)self.x[:, :, t] = torch.squeeze(xt,2)self.sigma[:, :, :, t] = sigmat