数据结构03(Java)--(递归行为和递归行为时间复杂度估算,master公式)
前言
本文为本小白🤯学习数据结构的笔记,将以算法题为导向,向大家更清晰的介绍数据结构相关知识(算法题都出自🙌B站马士兵教育——左老师的课程,讲的很好,对于想入门刷题的人很有帮助👍)
已经了解过排序了,在来了解一下递归行为和递归行为时间复杂度估算(master公式)
🙌还是先来看一个问题:
用递归方法找一个数组中的最大值,系统上到底是怎么做的?
package DiGui;public class Digui01 {public static int getMax(int[] arr) {return process(arr,0,arr.length-1);}//用递归方法找一个数组中的最大值,系统上到底是怎么做的?public static int process(int[] arr,int L,int R) {if(L==R){return arr[L];}int mid=L + ((R-L)>>1);//求中点int leftMax=process(arr,L,mid);int rightMax=process(arr,mid+1,R);return Math.max(leftMax,rightMax);}
}
来看看递归的核心思想:把大问题分解成小问题,小问题再分解,直到不能再分(基础情况),然后逐层合并结果。
- 把数组从中间分成两半;
- 分别找出左半部分的最大值和右半部分的最大值;
- 然后取这两个最大值中的较大者,就是整个区间的最大值。

利用函数一步步的往下分,直到到达最后一层,返回比较一步一步找到最大值。
递归行为时间复杂度如何估算?
来看看什么是master公式:
🌟 一、Master 公式是干什么的?
Master 公式(Master Theorem)是算法分析中一个非常重要的工具,用来快速求解递归算法的时间复杂度,特别是那些采用分治策略(Divide and Conquer)的算法,比如你上面写的递归找最大值、归并排序、快速排序(平均情况)等。
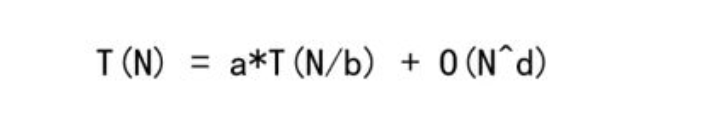
其中:
- n:问题规模
- a>=1:子问题的个数,(递归调用次数)
- b>=1:每个子问题的规模原问题的1/b(注:也就是说每个子问题规模是一样的)
- f(n): 非递归部分的工作量
看到这个公式,是不是一脸懵,这怎么计算n呢?嗯最重要的来了,这有一个公式(跟着算就好,我也不到杂咋推的🤪):

🙌我们来用master来算一下,上面代码的时间复杂度:
其中n = R- L + 1 是当前处理的数组长度
每次递归将问题分成两个子问题,每个子问题规模是原问题的一半:
- 左半:[L, mid]
- 右半:[mid+1, R]
因此:子问题个数 a = 2 ,每个子问题规模是 n / b,b = 2
Math.max(leftMax,rightMax) 是常数时间:O (1),d = 0
将a,b,d,带入,🎉 最终答案:时间复杂度是 O(n)
小白啊!!!写的不好轻喷啊🤯如果觉得写的不好,点个赞吧🤪(批评是我写作的动力)
…。。。。。。。。。。。…
…。。。。。。。。。。。…
