算法第四十八天:单调栈part01(第十章)
1.每日温度
739. 每日温度 - 力扣(LeetCode)
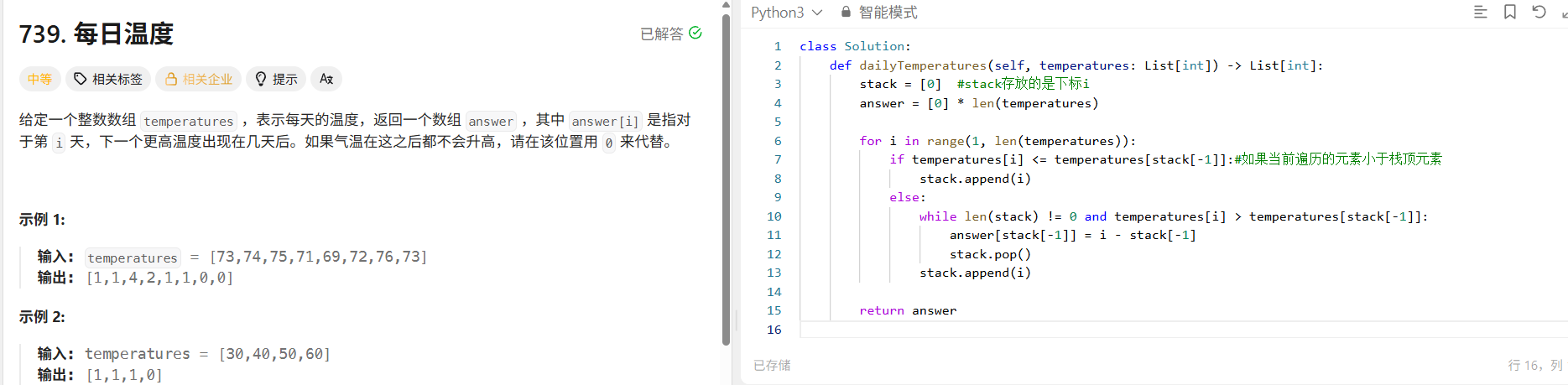
class Solution:def dailyTemperatures(self, temperatures: List[int]) -> List[int]:stack = [0] #stack存放的是下标ianswer = [0] * len(temperatures)for i in range(1, len(temperatures)):if temperatures[i] <= temperatures[stack[-1]]:#如果当前遍历的元素小于栈顶元素stack.append(i)else:while len(stack) != 0 and temperatures[i] > temperatures[stack[-1]]:answer[stack[-1]] = i - stack[-1]stack.pop()stack.append(i)return answer在使用单调栈的时候首先要明确如下几点:
- 单调栈里存放的元素是什么?
单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
- 单调栈里元素是递增呢? 还是递减呢?
注意以下讲解中,顺序的描述为 从栈头到栈底的顺序,因为单纯的说从左到右或者从前到后,不说栈头朝哪个方向的话,大家一定比较懵。
这里我们要使用递增循序(再强调一下是指从栈头到栈底的顺序),因为只有递增的时候,栈里要加入一个元素i的时候,才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
即:如果求一个元素右边第一个更大元素,单调栈就是递增的,如果求一个元素右边第一个更小元素,单调栈就是递减的。
文字描述理解起来有点费劲,接下来我画了一系列的图,来讲解单调栈的工作过程,大家再去思考,本题为什么是递增栈。
使用单调栈主要有三个判断条件。
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
把这三种情况分析清楚了,也就理解透彻了。
2.下一个更大元素Ⅰ
496. 下一个更大元素 I - 力扣(LeetCode)
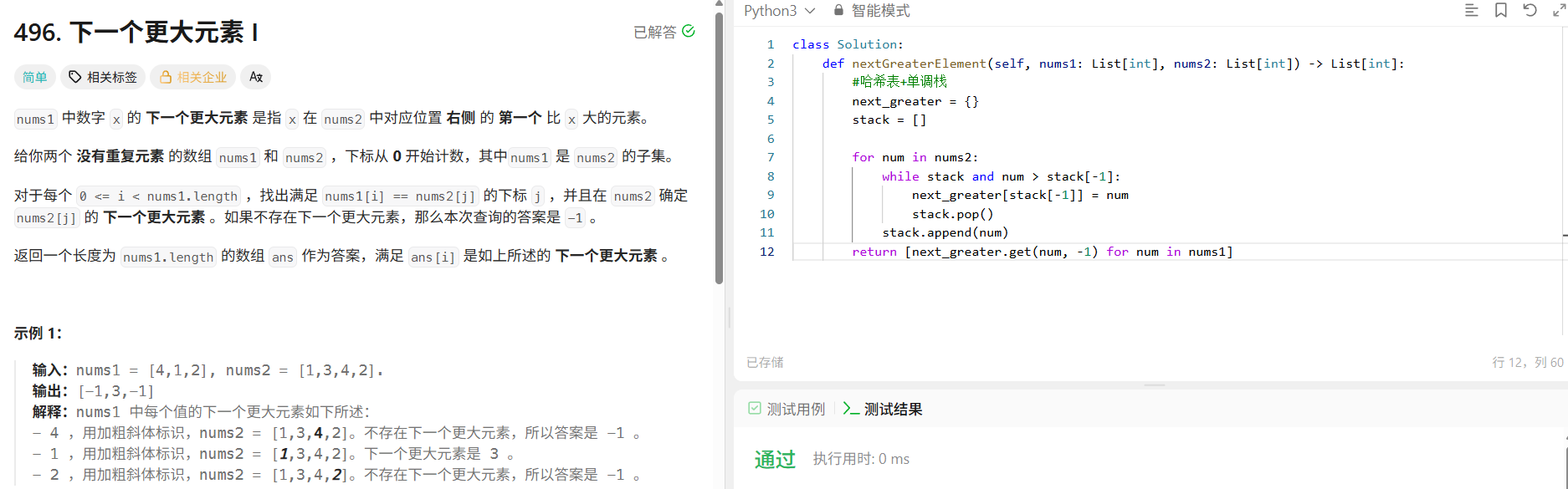
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:#哈希表+单调栈next_greater = {}stack = []for num in nums2:while stack and num > stack[-1]:next_greater[stack[-1]] = numstack.pop()stack.append(num)return [next_greater.get(num, -1) for num in nums1] 3.下一个更大元素II
503. 下一个更大元素 II - 力扣(LeetCode)
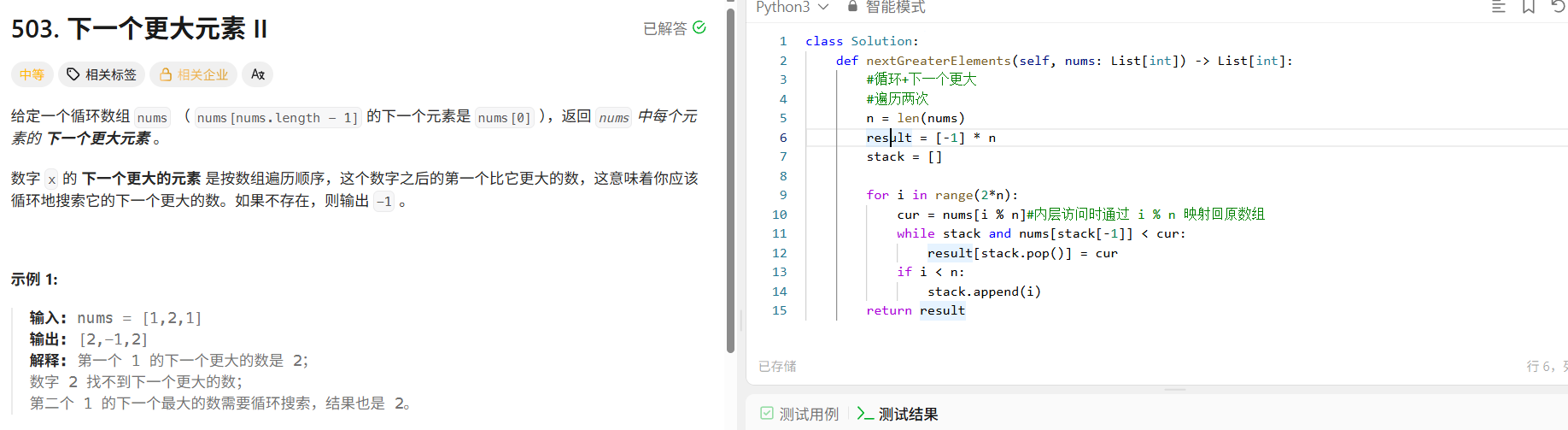
🔹 下一个更大元素 II 总结(循环数组版)
1️⃣ 问题本体
-
给定一个 循环数组
nums,求每个元素的 下一个更大元素。 -
如果不存在 → 返回
-1。 -
“循环数组”意味着最后一个元素后面接的是数组开头的元素,可以继续寻找。
2️⃣ 核心思路
-
单调栈:
-
栈里存 下标(而不是元素值)
-
栈保持 单调递减(栈顶元素最小)
-
当遍历到一个更大的元素时 → 弹出栈顶元素并更新答案
-
-
循环数组处理:
-
模拟循环:遍历两轮数组
0 ~ 2n-1 -
实际访问:
nums[i % n]→ 将下标映射回[0, n-1]
-
-
入栈限制:
-
只在 第一轮 i < n 时入栈
-
第二轮只用于更新答案,不入栈
-
避免下标越界和逻辑错误
-
3️⃣ 栈的作用
-
栈存放的是 “还没找到下一个更大元素的下标”
-
栈的大小 ≠ 答案个数
-
栈为空 → 表示当前没有待处理的元素
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:#循环+下一个更大#遍历两次n = len(nums)result = [-1] * nstack = []for i in range(2*n):cur = nums[i % n]#内层访问时通过 i % n 映射回原数组while stack and nums[stack[-1]] < cur:result[stack.pop()] = curif i < n:stack.append(i)return result今日份结束!
