C++ 力扣 904.水果成篮 题解 优选算法 滑动窗口 每日一题

这是封面原图，还有AI生成的动图（PS：豆哥现在新出个视频生成感觉挺好玩，个人觉得在某些方面比即梦免费的生成的视频好一点）

一、题目描述

题目链接：水果成篮

题目描述：

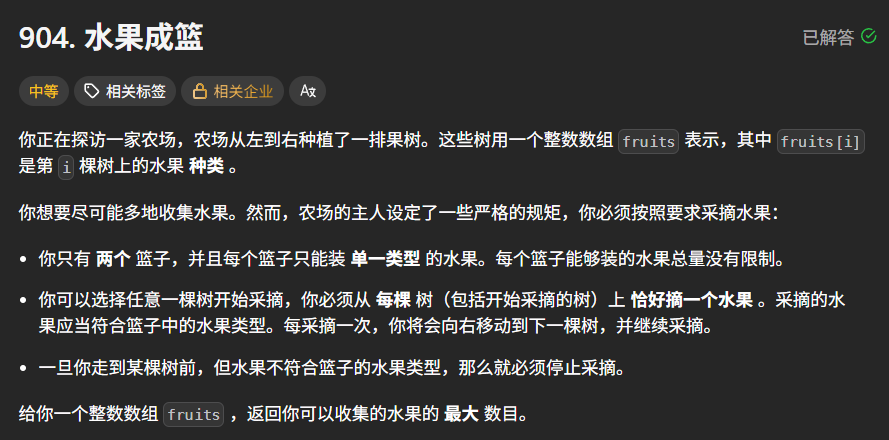
示例 1：
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。1 放入第一个篮子，2 放入第二个篮子，最后 1 放入第一个篮子。

示例 2：
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。0 不能摘，因为一开始若摘 0，后面 1 可放入第二个篮子，但再后面 2 无法放入；若从 1 开始，1 放一个篮子，2 放另一个，后面又一个 2 可放，共 3 个；从 2 开始（第二个 2）只能摘 2 个，所以最大是 3。

示例 3：
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。从 index=1 的 2 开始，2 放一个篮子，3 放另一个，后面两个 2 可放，共 4 个。

提示：
1 <= fruits.length <= 10^5
0 <= fruits[i] <= 10^5

二、为什么这道题值得你花时间琢磨？

水果成篮作为 LeetCode 第 904 题，是 滑动窗口在“限制元素种类”场景下的经典应用。它的价值主要体现在：

• 帮你深化对滑动窗口核心逻辑的理解——不仅能处理“特定和的子数组”，还能解决“元素种类受限的最长连续子数组”问题；
• 带你掌握“窗口内元素种类统计”的实现技巧，包括哈希表的常规用法和数组的取巧替代方案；
• 让你体会“优化数据结构”对算法效率的影响，尤其是在数据范围明确时，如何用更高效的方式替代通用结构。

学会这道题，你能更灵活地应对滑动窗口的各类变体，比如“最多包含k个不同字符的最长子串”“替换后的最长重复字符”等问题。

生活中也有类似场景，比如“超市里用固定几个袋子装指定品类的商品，求一次能拿的最多数量”“用有限几个容器装同类型物品，求连续拿取的最大数量”，核心都是“在种类限制下找最长连续序列”。

三、题目拆解：抓住关键约束

结合题目要求和示例，核心要素如下：

1. 输入是整数数组 fruits，数组元素代表水果种类，长度可达 10⁵（需考虑效率）。
2. 约束是最多只能有 2 种不同的水果（对应两个篮子），且子数组必须连续（因为要从左到右依次采摘，不能跳过）。
3. 目标是找到符合约束的最长子数组的长度，这个长度就是能收集的最大水果数。

关键点提炼：

• 核心约束：子数组中不同元素的种类≤2，这是滑动窗口需要维护的“有效性条件”；
• 目标明确：求“满足约束的最长连续子数组长度”，滑动窗口的典型应用场景；
• 效率要求：数组长度达10⁵，需保证算法时间复杂度在 O(n) 级别，避免嵌套循环；
• 统计重点：需要实时记录窗口内元素的种类数，这是判断窗口是否有效的关键。

四、思路演进：从暴力到滑动窗口

1. 暴力解法的困境

最直观的思路是用两个变量循环枚举所有可能的连续子数组，统计每个子数组的水果种类数，找出种类≤2的最长子数组。

• 枚举方式：
  固定子数组的起始位置 i，然后从 i 开始向右扩展终点 j，同时用一个集合记录子数组 [i,j] 中的水果种类，当种类超过2时停止，记录当前长度 j-i。

• 为什么不可行：
  时间复杂度是 O(n²)，对于 n=10⁵ 的数组，会产生 10¹⁰ 次操作，必然超时。而且每次枚举都要重新统计种类，重复计算多，效率极低。

结论：必须用滑动窗口优化，通过“一次遍历+动态维护窗口”将时间复杂度降至 O(n)。

2. 滑动窗口的思路：维护“种类≤2”的窗口

滑动窗口的核心是用两个指针 left 和 right 标记窗口的左右边界，通过移动指针动态调整窗口，始终保证窗口内的元素满足“种类≤2”，同时记录窗口的最大长度。

步骤拆解：

• 初始化：left=0（窗口左边界），right=0（窗口右边界），用一个“计数器”记录窗口内每种水果的数量，用一个变量记录当前窗口的水果种类数。
• 扩展窗口：移动 right，将 fruits[right] 加入窗口，更新计数器和种类数。
• 维护窗口有效性：若窗口内种类数>2，说明当前窗口无效，需要移动 left 缩小窗口，同时更新计数器（减少 fruits[left] 的数量，若数量减为0则减少种类数），直到种类数≤2。
• 更新结果：每次扩展或缩小窗口后，若窗口有效（种类数≤2），就用当前窗口长度 right-left+1 更新最大长度。

关键问题：如何统计窗口内的种类数？

这是本题的核心实现点，有两种常见方式：

• 哈希表（通用方案）：用 unordered_map<int, int> 存储“水果种类-数量”的映射，通过哈希表的大小判断种类数（哈希表的key数量就是种类数）；
• 数组（取巧方案）：若已知水果种类的范围（题目提示 0≤fruits[i]≤10⁵），可用一个数组代替哈希表，数组下标代表水果种类，值代表数量，再用一个变量单独记录种类数。

五、算法实现：从哈希表到数组优化

1. 哈希滑动窗口（通用实现）

class Solution {
public:int totalFruit(vector<int>& fruits) {unordered_map<int,int> hashi;  // 哈希表：key为水果种类，value为该种类在窗口内的数量int ret = 0;  // 存储最终结果：能收集的最大水果数// 滑动窗口双指针：left为左边界，right为右边界，初始均从0开始for(int left = 0,right = 0;right < fruits.size();right++){// 将当前右边界的水果加入窗口，对应种类的数量+1hashi[fruits[right]]++;// 当窗口内水果种类超过2种时，需要收缩左边界以保证窗口有效while(hashi.size() > 2){// 左边界水果的数量-1hashi[fruits[left]]--;// 若该种类水果数量减为0，说明窗口内已无此种类，从哈希表中删除（保证size准确）if(hashi[fruits[left]] == 0)hashi.erase(fruits[left]);// 左边界右移，缩小窗口范围left++;}// 每次调整窗口后，计算当前窗口长度（right-left+1），更新最大长度retret = max(ret , right - left + 1);}return ret;}
};

2. 数组代替哈希表（优化实现）

class Solution {
public:int totalFruit(vector<int>& fruits) {// 数组代替哈希表：下标对应水果种类（因提示0≤fruits[i]≤10^5，故大小设为100001）// 数组值代表该种类水果在窗口内的数量，初始全为0int hashi[100001] = {0};int ret = 0;  // 存储最终结果：能收集的最大水果数// 滑动窗口双指针+种类计数器：left左边界，right右边界，mark记录窗口内水果种类数for(int left = 0,right = 0, mark = 0;right < fruits.size();right++){// 若当前水果种类在窗口内数量为0，说明是新种类，种类数mark+1if(hashi[fruits[right]] == 0)mark++;// 当前水果种类的数量+1hashi[fruits[right]]++;// 当窗口内种类数超过2时，收缩左边界while(mark > 2){// 左边界水果的数量-1hashi[fruits[left]]--;// 若该种类数量减为0，说明窗口内已无此种类，种类数mark-1if(hashi[fruits[left]] == 0)mark--;// 左边界右移，缩小窗口left++;}// 计算当前窗口长度，更新最大长度retret = max(ret , right - left + 1);}return ret;}
};

六、两种实现的对比分析

实现方式	核心数据结构	时间复杂度	空间复杂度	适用场景
哈希滑动窗口	unordered_map	O(n)	O(1)（最多存3种）	水果种类范围不确定的通用场景
数组代替哈希表	固定大小的数组	O(n)	O(MAX_TYPE)	水果种类范围明确且不大的场景

• 时间上：两者理论均为 O(n)，但数组版本无需哈希计算，冲突处理和频繁的erase，实际运行更快；
• 空间上：哈希表版本为常数空间（最多存3种水果），数组版本空间取决于种类最大值（本题10⁵+1属可接受范围）；
• 灵活性上：哈希表更通用，若种类范围未知或极大（如10⁹），只能用哈希表。

七、实现过程中的坑点总结

1. 哈希表未删除数量为0的元素

   • 错误：收缩窗口时只减少数量，不删除key，导致 hashi.size() 大于实际种类数（如某种水果已无，却仍在哈希表中）。
   • 解决：当 hashi[fruits[left]] 减为0时，必须 erase 该key，确保size准确。

2. 数组大小不足或未初始化

   • 错误：数组大小小于水果最大种类（如设为10⁵但存在10⁵的种类）导致越界；或未初始化（局部数组默认非0），导致 mark 统计错误。
   • 解决：按提示设足大小（如100001），并显式初始化 {0}。

3. 收缩窗口用if而非while

   • 错误：hashi.size()>2 时用if收缩一次，可能无法将种类数压回≤2（如窗口内有3种水果，一次收缩可能仍剩2种以上）。
   • 解决：必须用while循环收缩，直到种类数≤2。

4. 窗口长度计算错误

   • 错误：用 right-left 计算长度（如left=1、right=3时，窗口有3个元素，却算成2）。
   • 解决：窗口长度为 right-left+1（闭区间 [left,right] 的元素个数）。

八、思考：滑动窗口的核心是什么？

这道题和“将x减到0的最小操作数”虽场景不同，但滑动窗口的核心逻辑一致：用双指针维护一个“有效区间”，通过动态调整指针减少重复计算，将O(n²)优化为O(n)。

区别在于“有效性条件”：前者是“元素和=target”，后者是“元素种类≤2”。但本质都是——明确“窗口有效”的标准，在扩展时记录可能的解，在无效时收缩边界，最终遍历一次得到最优解。

九、下题预告

明天将讲解 438. 找到字符串中所有字母异位词，这是滑动窗口在字符串匹配中的经典应用。

提前思考方向：

• 字母异位词的核心是“字符种类和数量完全相同”，如何用滑动窗口匹配？
• 如何高效统计窗口内字符与目标字符串的字符频率？
• 窗口长度是否固定？若固定，如何优化滑动时的频率更新？

如果觉得这篇解析有帮助，不妨：
🌟 点个赞，让更多人看到这份清晰思路
⭐ 收个藏，下次复习时能快速找回灵感
👀 加个关注，明天见！