时间复杂度、空间复杂度和渐近符号(O、Ω、Θ 等)
📊 算法复杂度综合分析表
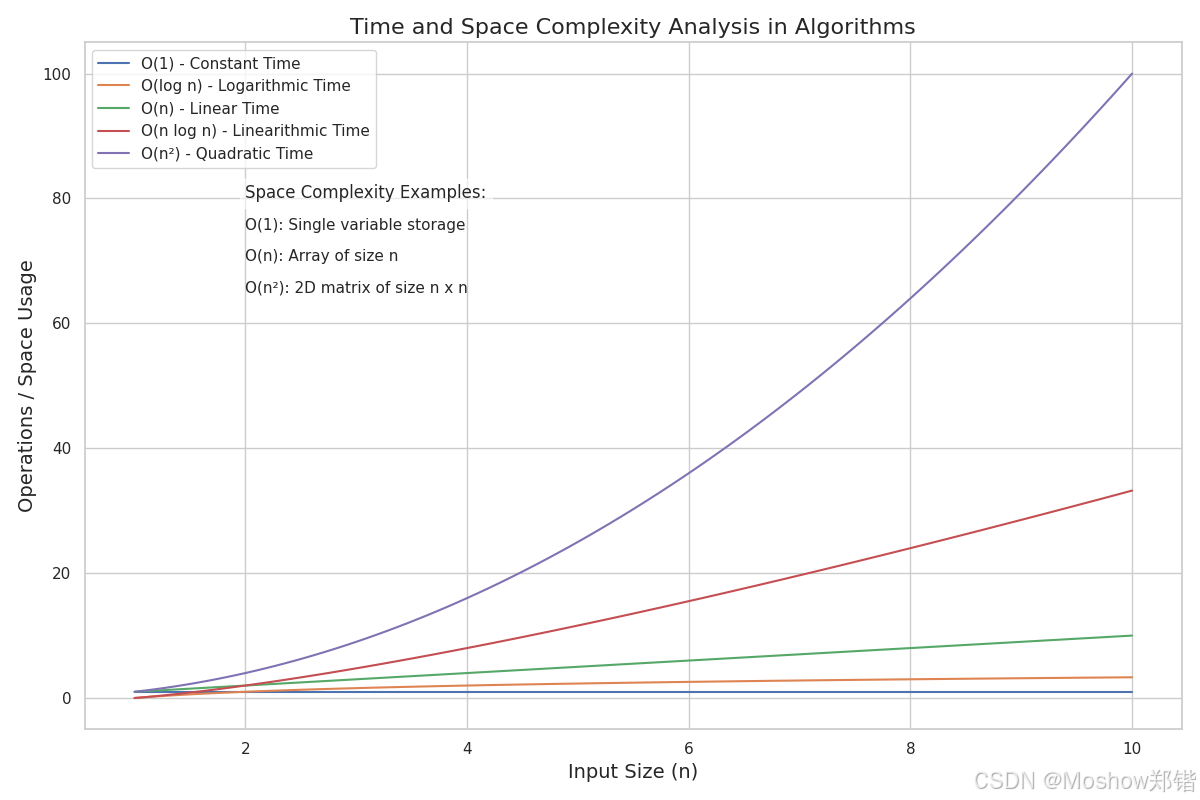
| 类别 | 常见表示 | 含义解释 | 渐近符号含义 | 主要影响因素 |
|---|---|---|---|---|
| 时间复杂度 | $$O(1), O(\log n), O(n), O(n\log n), O(n^2)$$ 等 | 衡量算法随输入规模 nn 增长时,运行时间的增长趋势 | O(上界/最坏情况)<br>Ω(下界/最好情况)<br>Θ(上下界一致,精确渐近)<br>o(严格小于)<br>ω(严格大于) | - 输入规模 nn<br>- 数据结构选择<br>- 算法设计思想(递归、分治、动态规划等)<br>- 最佳/最差/平均情况分析 |
| 空间复杂度 | $$O(1), O(n), O(n^2)$$ 等 | 衡量算法运行时所需的额外内存空间随输入规模 nn 的变化情况 | 同上(渐近符号也适用空间分析) | - 临时变量/辅助存储<br>- 递归栈深度<br>- 数据存储结构(数组、链表、矩阵等)<br>- 缓存策略 |
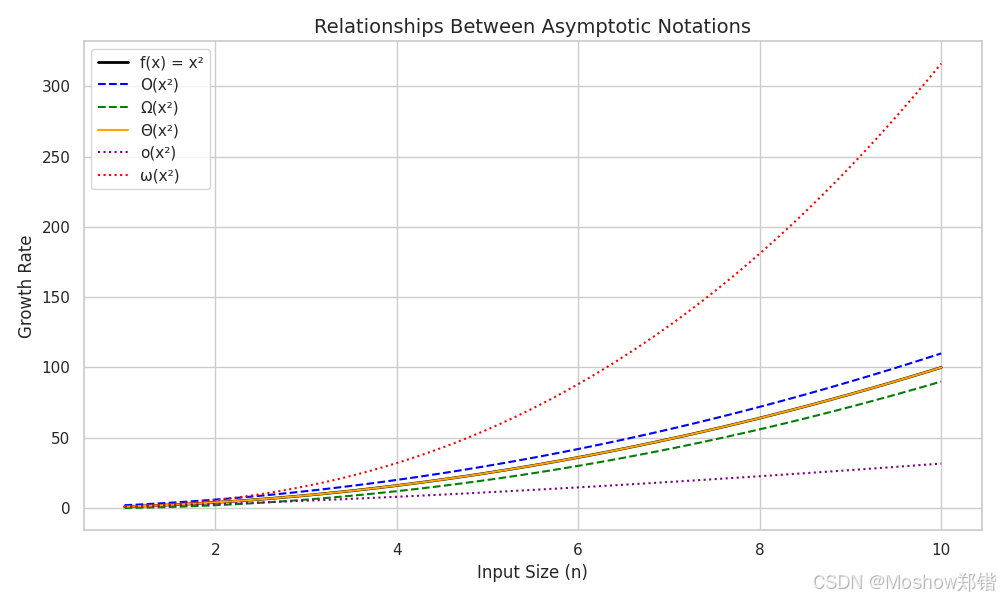
📌 渐近符号速览表
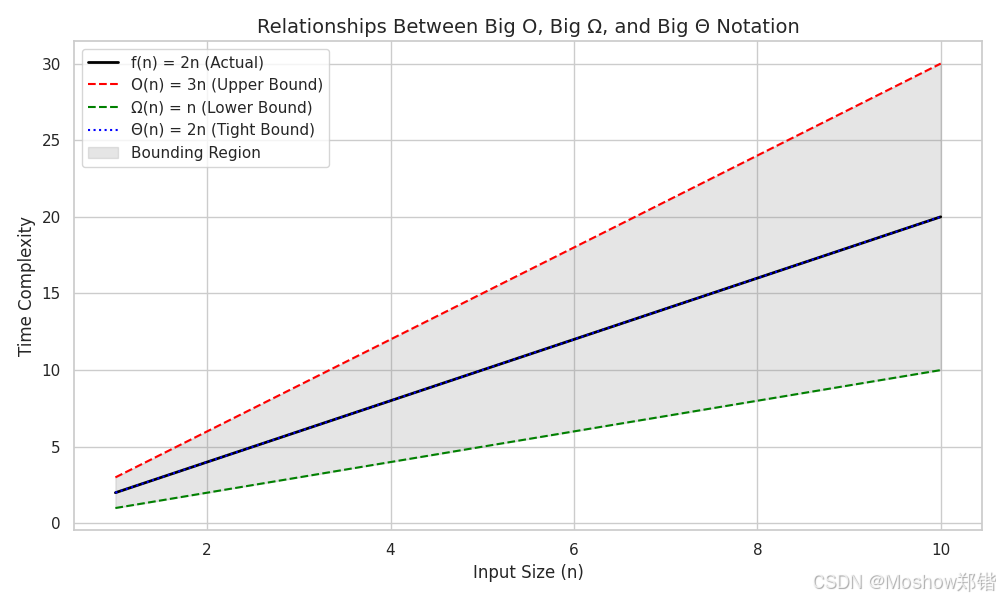
| 符号 | 读法 | 意义 | 适用场景 |
|---|---|---|---|
| O | Big-O | 上界,最坏情况不超过某个函数的常数倍 | 最坏复杂度分析 |
| Ω | Big-Omega | 下界,最好情况至少达到某个函数的常数倍 | 最好复杂度分析 |
| Θ | Big-Theta | 上下界一致,精确描述增长率 | 精确复杂度 |
| o | Small-o | 严格小于某个增长率 | 理论推导 |
| ω | Small-omega | 严格大于某个增长率 | 理论推导 |
💡 记忆小技巧
-
O = "不超过"(上限)
-
Ω = "不少于"(下限)
-
Θ = “刚刚好”上下限都一致
-
o/ω 更偏理论,用于严格比较增长率
整理 by Moshow郑锴@https://zhengkai.blog.csdn.net/
