P5663 [CSP-J2019] 加工零件

题目传送门

前言：666，又是一道压轴题，BFS求1~n的最短路就能过。这好像是第一年的CSP—J的压轴题，听说在2019年NOIP被取消了，然后不知道咋了又恢复了，有没有大佬懂得这是为啥，在评论区帮忙回答一下，谢谢qwq

题解：

题目意思：

题目意思就是说如果这个零件需要轩轩帮助，而且他到那个员工的最短路是小于员工的加工零件阶段的话，即可。

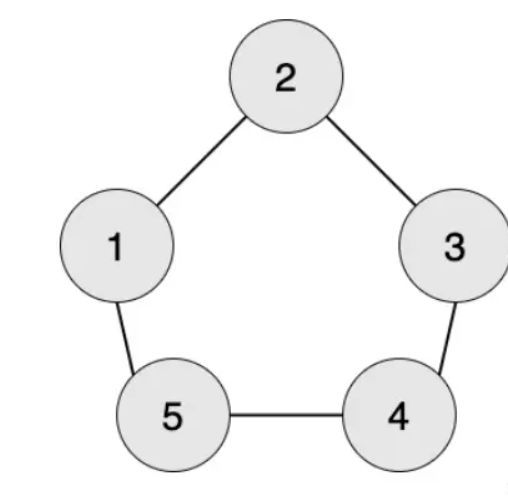
如该图，假设3号工人要加工第三阶段的，因为轩轩只能提供原材料给下一个工人而自己无法生产，所以我们得出一个结论，如果该节点需要加工的零件阶段是奇数的话，那么若想要轩轩提供零件的话，那么他们之间的最短路径必须是一个奇数，否则轩轩无法传递给该工人，反之若果该节点的加工零件阶段是一个偶数的话，那么轩轩与该节点的最短路径必须是一个偶数才行，否则轩轩仍然无法给该员工提供零件

还是按照刚刚的例子：

这里我们求出了1和3之间的偶数最短路径为2，技术最短路径为3，而三号工人如果需要一个阶段是3的零件，那么轩轩完全可以选择奇数最短路来为3号员工提供零件，所以我们就知道了这道题的大体思路了，那么我们应该想想如何实现这些功能

实现：

首先我们这次求最短路用到的方式是BFS（广度优先搜索），利用奇数最短路与偶数最短路和当前的部署作比较来得出当前这个点的步数是否适合做该点的奇数最短路或偶数最短路，然后将它们单独存入一个数组并进行不断比较，当然这里有一个细节，就是要对奇数最短路与偶数最短路的数组初始值进行初始化，这里建议使用0x3f,不建议使用0x7f否则可能会爆int（虽然0x7f是int类型的临界值，但不建议）

int n,m,q;
int ji[100005],ou[100005];
struct node{int o;int cnt;
}; 
queue<node> qu;
void bfs(){memset(ji,0x3f,sizeof ji);memset(ou,0x3f,sizeof ou);for(int i=0;i<G[1].size();i++){ji[G[1][i]]=1;qu.push((node){G[1][i],1});}while(!qu.empty()){int t_o=qu.front().o;int t_c=qu.front().cnt;qu.pop();for(int i=0;i<G[t_o].size();i++){int q=t_c+1;if(q<ji[G[t_o][i]]||q+1<ou[G[t_o][i]]){if(q%2==0&&q<ou[G[t_o][i]]){qu.push((node){G[t_o][i],q});ou[G[t_o][i]]=q;}if(q%2==1&&q<ji[G[t_o][i]]){qu.push((node){G[t_o][i],q});ji[G[t_o][i]]=q;}}}}return ;
}

这里注意一种情况（）：

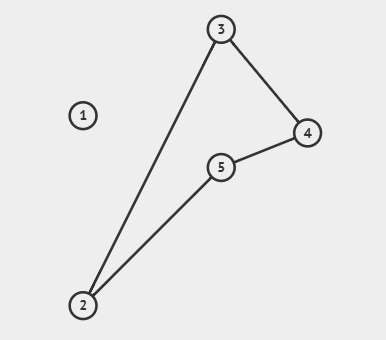
这种情况是一号是一个单独的联通分量，如果直接把他BFS队列里的话，就会WA。为什么呢？原因是一个点到自己的最短路是0如果把自己也算进去的话，这就是一个重边，而题目中说了这样一句话：x 号工人自己无需生产第 L−1 阶段的零件，很明显，这句话就是告诉我们这道题目中的图是不存在重边的，所以如果加进去，一定会WA的，所以在上面的代码里，我们单独把1号节点拉出来，把他的所有邻接点存进去，而不存1号节点就可以避免此问题

主函数的话除了输入就是判定了，和上述说的思路一样，只要这个L是奇数，那么就让ji[a]与L去比较，r如果L是个偶数的话，就让ou[a]与L去比较，如果L更大输出Yes，反之则输出No,这样的话就可以判别了

while(q--){int a,L;scanf("%d%d",&a,&L);if(L%2==0){if(ou[a]>L){printf("No\n");}else{printf("Yes\n");}}else{if(ji[a]>L){printf("No\n");}else{printf("Yes\n");}}}

AC 代码：

#include<bits/stdc++.h>
using namespace std;
vector<int> G[100005];
int n,m,q;
int ji[100005],ou[100005];
struct node{int o;int cnt;
}; 
queue<node> qu;
void bfs(){memset(ji,0x3f,sizeof ji);memset(ou,0x3f,sizeof ou);for(int i=0;i<G[1].size();i++){ji[G[1][i]]=1;qu.push((node){G[1][i],1});}while(!qu.empty()){int t_o=qu.front().o;int t_c=qu.front().cnt;qu.pop();for(int i=0;i<G[t_o].size();i++){int q=t_c+1;if(q<ji[G[t_o][i]]||q+1<ou[G[t_o][i]]){if(q%2==0&&q<ou[G[t_o][i]]){qu.push((node){G[t_o][i],q});ou[G[t_o][i]]=q;}if(q%2==1&&q<ji[G[t_o][i]]){qu.push((node){G[t_o][i],q});ji[G[t_o][i]]=q;}}}}return ;
}
int main(){scanf("%d%d%d",&n,&m,&q);while(m--){int x,y;scanf("%d%d",&x,&y);G[x].push_back(y);G[y].push_back(x);}bfs();while(q--){int a,L;scanf("%d%d",&a,&L);if(L%2==0){if(ou[a]>L){printf("No\n");}else{printf("Yes\n");}}else{if(ji[a]>L){printf("No\n");}else{printf("Yes\n");}}}return 0;
}