机器学习--KNN算法
一、KNN近邻分类算法
1、常用距离计算方法
常用的距离计算方法有 欧几里得距离、曼哈顿距离,以下是两种方法图示
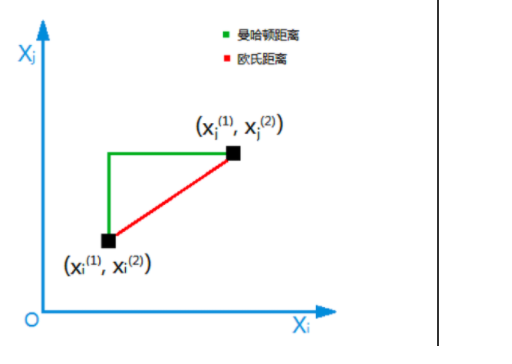
1.1 欧几里得距离
欧几里得距离是最常见的距离度量方式之一,它适用于连续特征空间中的点到点之间的距离计算,给定两个n维向量 x=(x1,x2,...,xn) 和 𝑦=(𝑦1,𝑦2,...,𝑦𝑛),它们之间的欧几里得距离定义为:
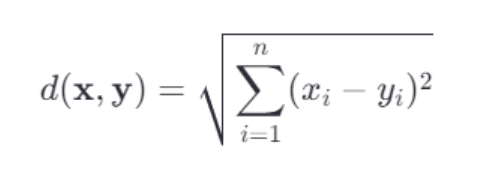
1.2 曼哈顿距离
曼哈顿距离又称为城市街区距离,它衡量的是两点之间沿着坐标轴方向的总距离。对于上述同样定义的两个 n 维向量 𝑥 和 𝑦,它们之间的曼哈顿距离定义为:
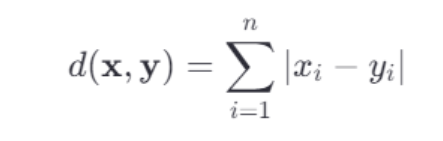
2、概述
KNN 算法两个关键词,一个是少数服从多数,另一个是距离,它们是实现 KNN 算法的核心知识
KNN 算法属于分类算法的一种
原理:
为了判断未知样本的类别,以所有已知类别的样本作为参照来计算未知样本与所有已知样本的距离,然后从中选取与未知样本距离最近的 K 个已知样本,并根据少数服从多数的投票法则(majority-voting),将未知样本与 K 个最邻近样本中所属类别占比较多的归为一类
在 scikit-learn 中 KNN 算法的 K 值是通过 n_neighbors 参数来调节的,默认值是 5
KNN 算法简单易于理解,无须估计参数,与训练模型,适合于解决多分类问题,面对样本不平衡时,需要调节权重参数,否则误差很大
KNN 分类算法适用于多分类问题、OCR光学模式识别、文本分类等领域
KNN 分类算法主要包括以下 4 个步骤:
准备数据,对数据进行预处理
计算测试样本点到其他每个样本点的距离
对每个距离进行排序,然后选择出距离最小的 K 个点
对 K 个点所属的类别进行比较,按照少数服从多数的原则,将测试样本点归入到 K 个点中占比最高的一类中
KNN 缺点:
k 值取得过小,容易受到异常点的影响
k 值取得过大,样本不均衡的影响
3、KNN 分类算法实现
Pyhthon Sklearn 机器学习库提供了 neighbors 模块,该模块下提供了 KNN 算法的常用方法
3.1 函数
| 方法 | 参数 | 说明 |
|---|---|---|
| KNeighborsClassifier | n_neighbors:指定 k 值的大小,默认值 5 | KNN 算法解决分类问题 |
3.2 红酒数据集预测
存在一个警告,修改源码,加一个参数 keepdims=False
# 从 scikit-learn 库导入线性模型中的 KNN 算法 from sklearn import neighbors # 导入 sklearn 中的自带的数据集 from sklearn.datasets import load_wine # skleran 提供的分割数据集 from sklearn import model_selection import numpy as np import random from sklearn.preprocessing import StandardScaler def wine_test():wine_dataset = load_wine()'''data 是数据内容、target 为样本标签'''wine_data = wine_dataset['data']wine_target = wine_dataset['target']# 划分训练集数据和测试集数据x_train, x_test, y_train, y_test = model_selection.train_test_split(wine_data,wine_target,random_state=42)# 特征工程:标准化standardScaler = StandardScaler()x_train = standardScaler.fit_transform(x_train)x_test = standardScaler.transform(x_test)# 创建模型,n_neighbors 参数指定 K 值model = neighbors.KNeighborsClassifier(n_neighbors=4)# 训练模型model.fit(x_train, y_train)# 使用模型对测试集分类预测,并打印分类结果y_predict = model.predict(x_test)print(y_predict == y_test)# 用测试集对模型进行评分print(model.score(x_test, y_test))# 设置数据,用于测试data_test = []data_test.append(random.sample(range(1000), 13))print(data_test)x_wine_test = np.array(data_test)wine_predict = model.predict(x_wine_test)print(wine_predict) wine_test()
4、练习
使用代码实现,取 k=5,计算出唐人街探案属于什么电影类型
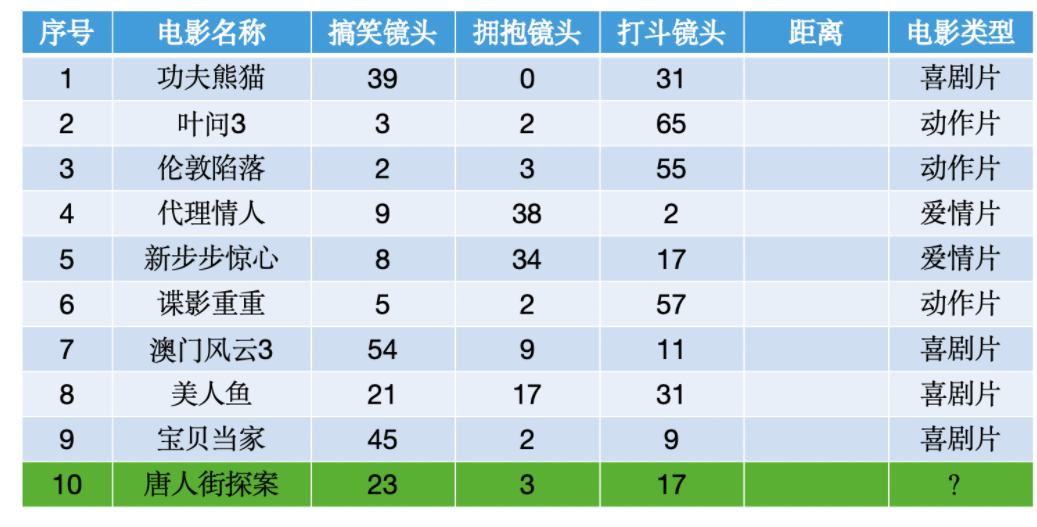
实现:
import math
# 唐人街探案数据预测
def predic_movie():movie_data = {"功夫熊猫": [39, 0, 31, "喜剧片"],"叶问3": [3, 2, 65, "动作片"],"伦敦陷落": [2, 3, 55, "动作片"],"代理情人": [9, 38, 2, "爱情片"],"新步步惊心": [8, 34, 17, "爱情片"],"谍影重重": [5, 2, 57, "动作片"],"澳门风云3": [54, 9, 11, "喜剧片"],"美人鱼": [21, 17, 5, "喜剧片"],"宝贝当家": [45, 2, 9, "喜剧片"],}# 欧几里得距离公式计算tang = [23, 3, 17]result = []for key, v in movie_data.items():distance = math.sqrt((tang[0] - v[0]) ** 2 + (tang[1] - v[1]) ** 2 + (tang[2] - v[2]) ** 2)result.append([key, round(distance, 2)])# 距离从小到大排序result.sort(key=lambda x: x[1])# 取 k=5,选择距离最小的5个样本result = result[:5]# 统计 k=5 的时候样本的类型labels = {"喜剧片": 0, "动作片": 0, "爱情片": 0}for item in result:label = movie_data[item[0]] # 通过电影的名字找到电影的信息labels[label[3]] += 1 # 取出电影的类型,并统计数量labels = sorted(labels.items(), key=lambda l: l[1], reverse=True)print('k=5,电影类型为:', labels[0][0])1. model.fit(X_train, y_train) 在 k-NN 中到底做了什么?
对于大多数模型(如线性回归、神经网络等):
fit()方法会通过优化算法(如梯度下降)从训练数据中学习参数(如权重、规则)。这些模型会在训练阶段主动分析数据,构建一个泛化的“规则”。但对于 k-NN:
fit()方法 几乎什么都不做!它只是将X_train和y_train原封不动地存储到内存中,没有数学运算或规则推导。你可以认为
fit()的代码类似于:
Python def fit(self, X_train, y_train):self.X_train = X_train # 记住训练数据的坐标self.y_train = y_train # 记住训练数据的标签return self
为什么叫“惰性”? 因为模型在训练阶段“偷懒”,直到预测时(调用
predict())才临时计算距离和投票。
2. 如果训练阶段不“学习”,k-NN 如何判断新数据的类别?
关键在于 预测阶段(调用 predict() 时)的步骤:
输入测试点
x_test(例如[3, 3])。计算距离
:
模型将
x_test与所有存储的X_train点计算距离(如欧氏距离)。
选择邻居
:
找出距离最近的
k个训练点(如k=3)。
投票决策
:
查看这
k个邻居的标签(y_train中对应的值),通过多数表决预测类别。
