MySQL 索引算法
MySQL 索引算法
- 顺序查找
- 二分查找
- 二叉查找树
- 平衡二叉树
- B 树
- B+树
- B+ 树索引
https://algorithm-visualizer.org/branch-and-bound/binary-search
这个网站可以像看动画一样,观看算法执行,有助于理解。
如果打不开,可以搜索,在线算法工具,多试几个,有了这种工具,可以更好理解算法。
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
顺序查找
在一组数据中找到对应的记录,顺序查找是一个一个地扫描,直到找到对应的记录。
顺序查找对数据没有任何要求
时间复杂度
顺序查找的时间复杂度为 O(n),其中 n 是数据集的大小:
- 最好情况:目标元素在第一个位置,时间复杂度 O(1)
- 最坏情况:目标元素在最后一个位置或不存在,时间复杂度 O(n)
- 平均情况:目标元素在任意位置的概率相等,平均时间复杂度 O(n)
空间复杂度
顺序查找的空间复杂度为 O(1),因为它只需要固定的额外空间来存储索引和临时变量,不随数据集大小变化
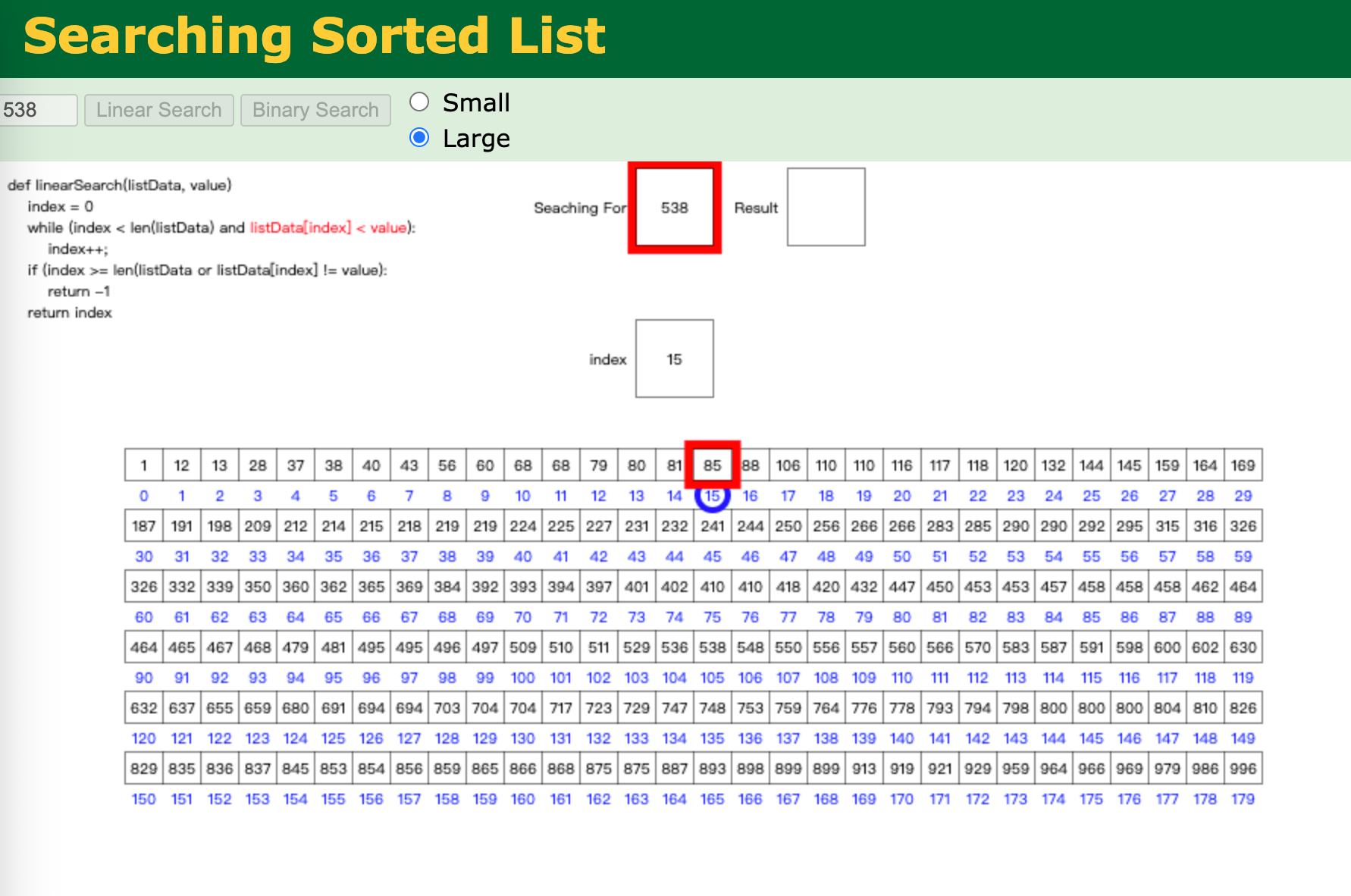
在以下数组中查找数字 7:
[2, 5, 1, 9, 3, 6, 7]
步骤1: [3, 8, 2, 7, 5, 9]↑比较3和7 -> 不相等步骤2: [3, 8, 2, 7, 5, 9]↑比较8和7 -> 不相等步骤3: [3, 8, 2, 7, 5, 9]↑比较2和7 -> 不相等步骤4: [3, 8, 2, 7, 5, 9]↑比较7和7 -> 相等,找到目标,返回索引3
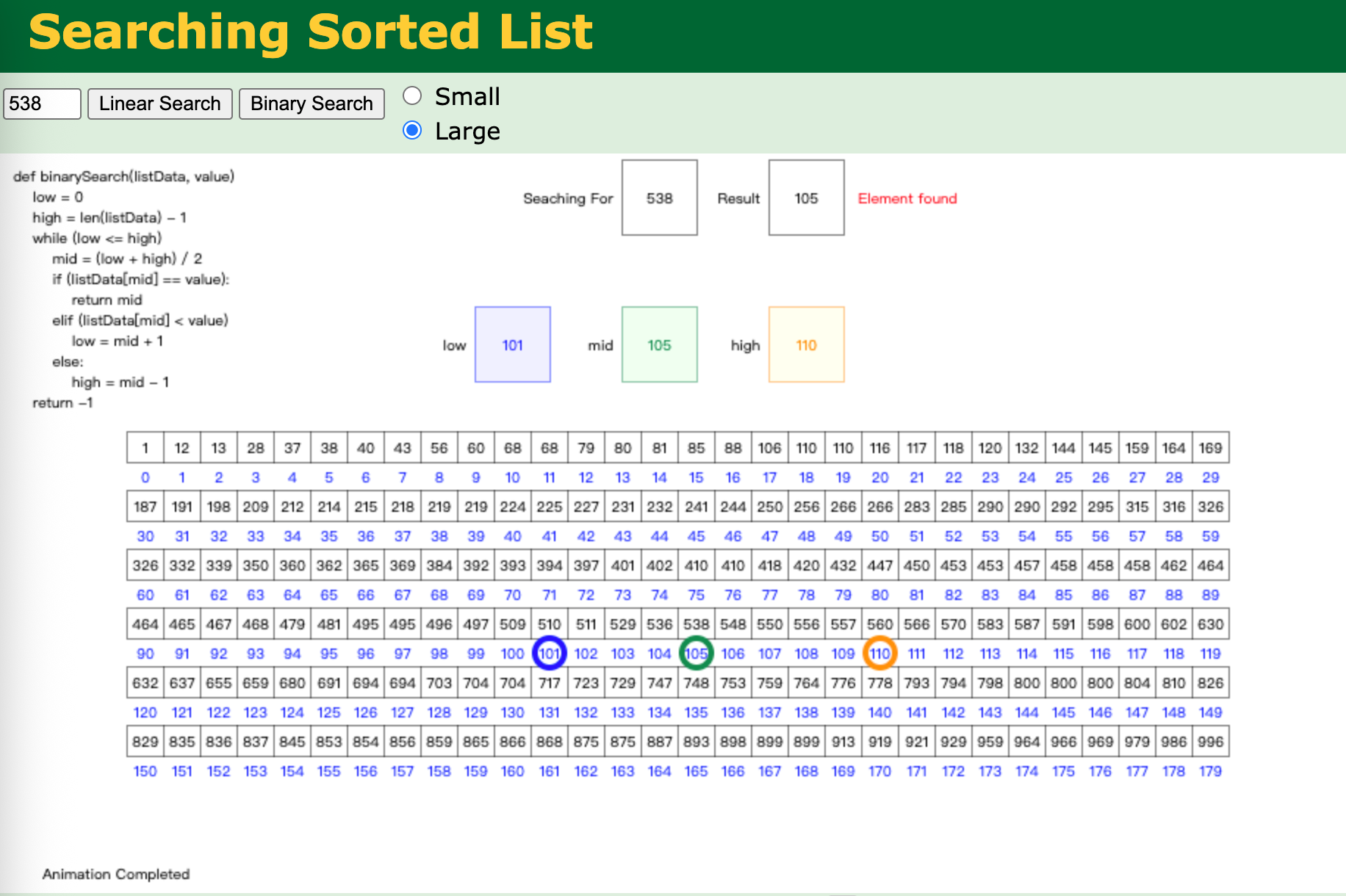
二分查找
二分查找是将记录顺序排列,查找时先将序列的中间元素作为比较对象。如果要找的元素的值小于该中间元素的值,那么只需要在前一半的元素中继续查找;如果要找的元素的值等于该中间元素的值,那么查找结束;如果要找的元素的值大于该中间元素的值,那么只需要在后一半元素中继续查找。
假设要在下面的数据中找到 19
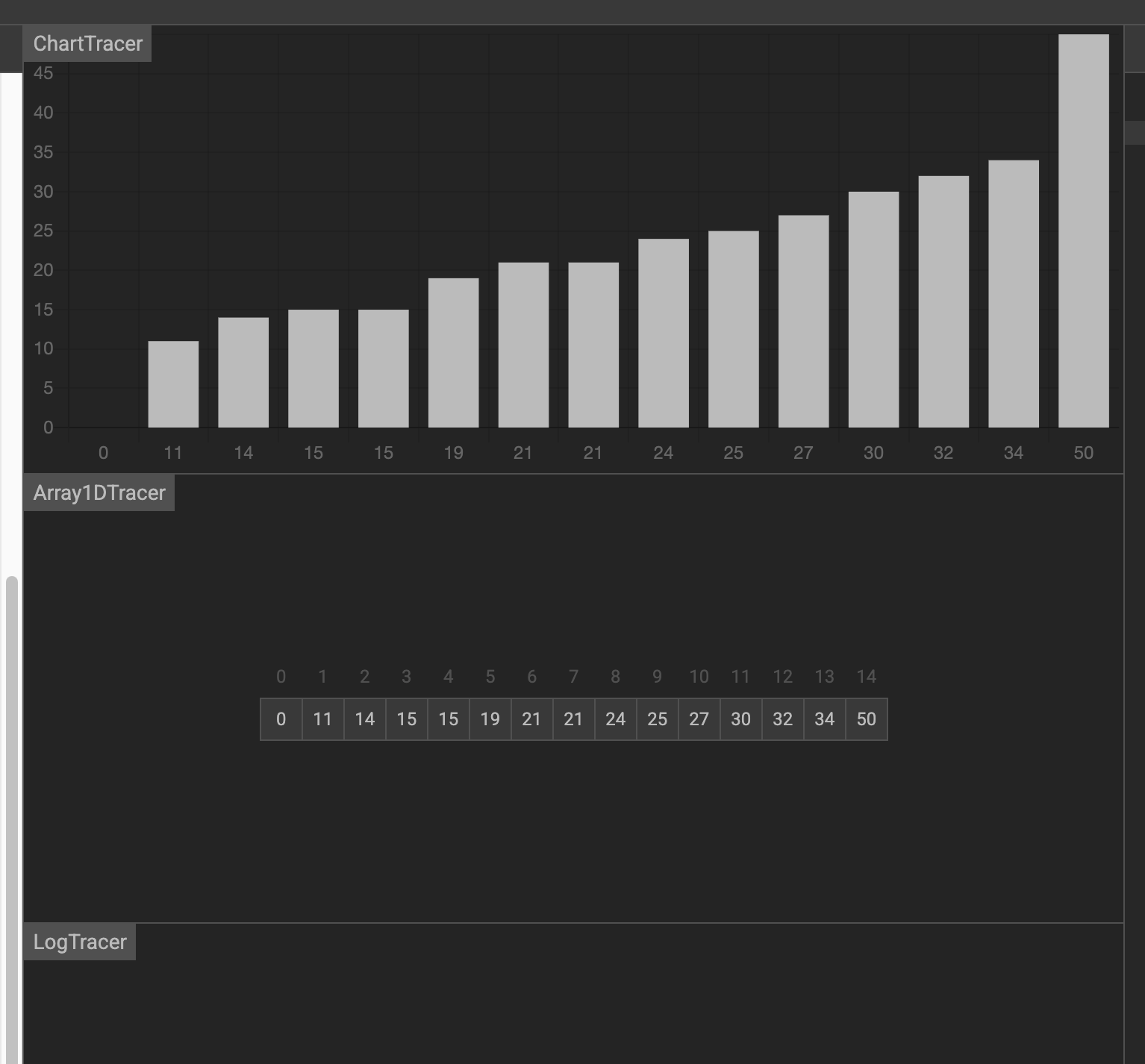
第一次,找到中间元素 21 ,大于19,前一半
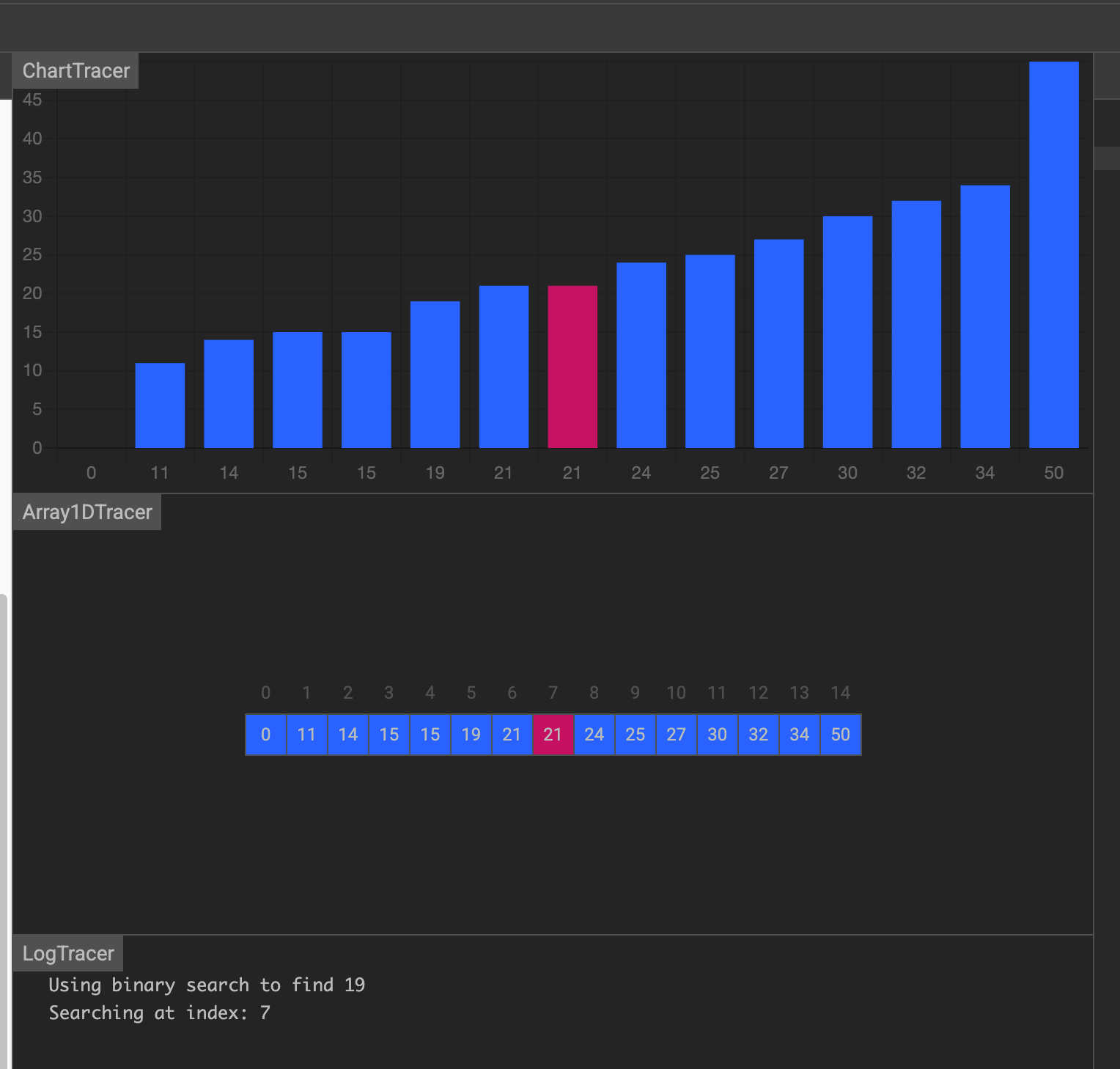
第二次,在前一半中找到中间元素15,小于19,在后一半中
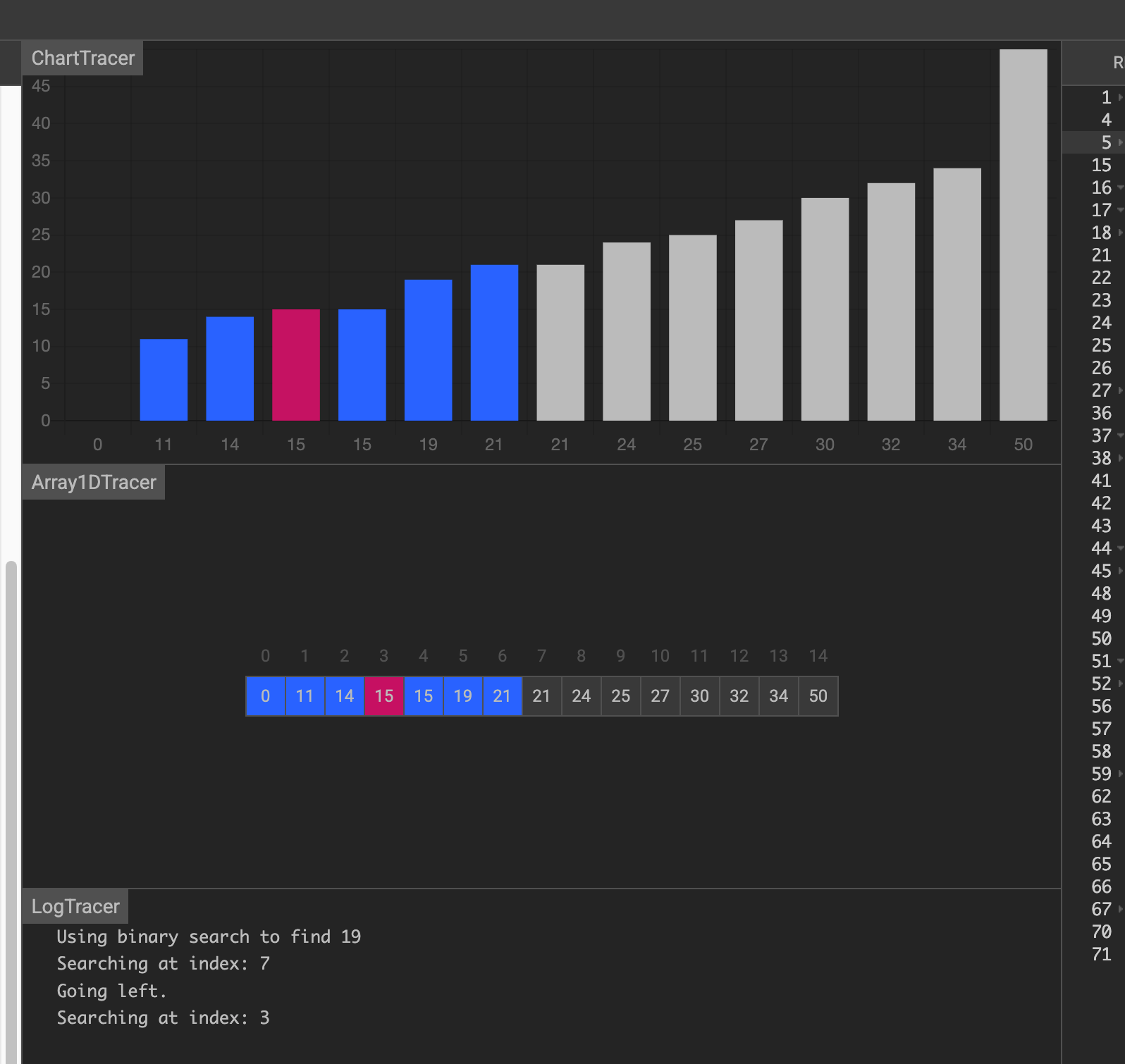
第三次,在后一半中找到中间元素19,刚好相等,找到了
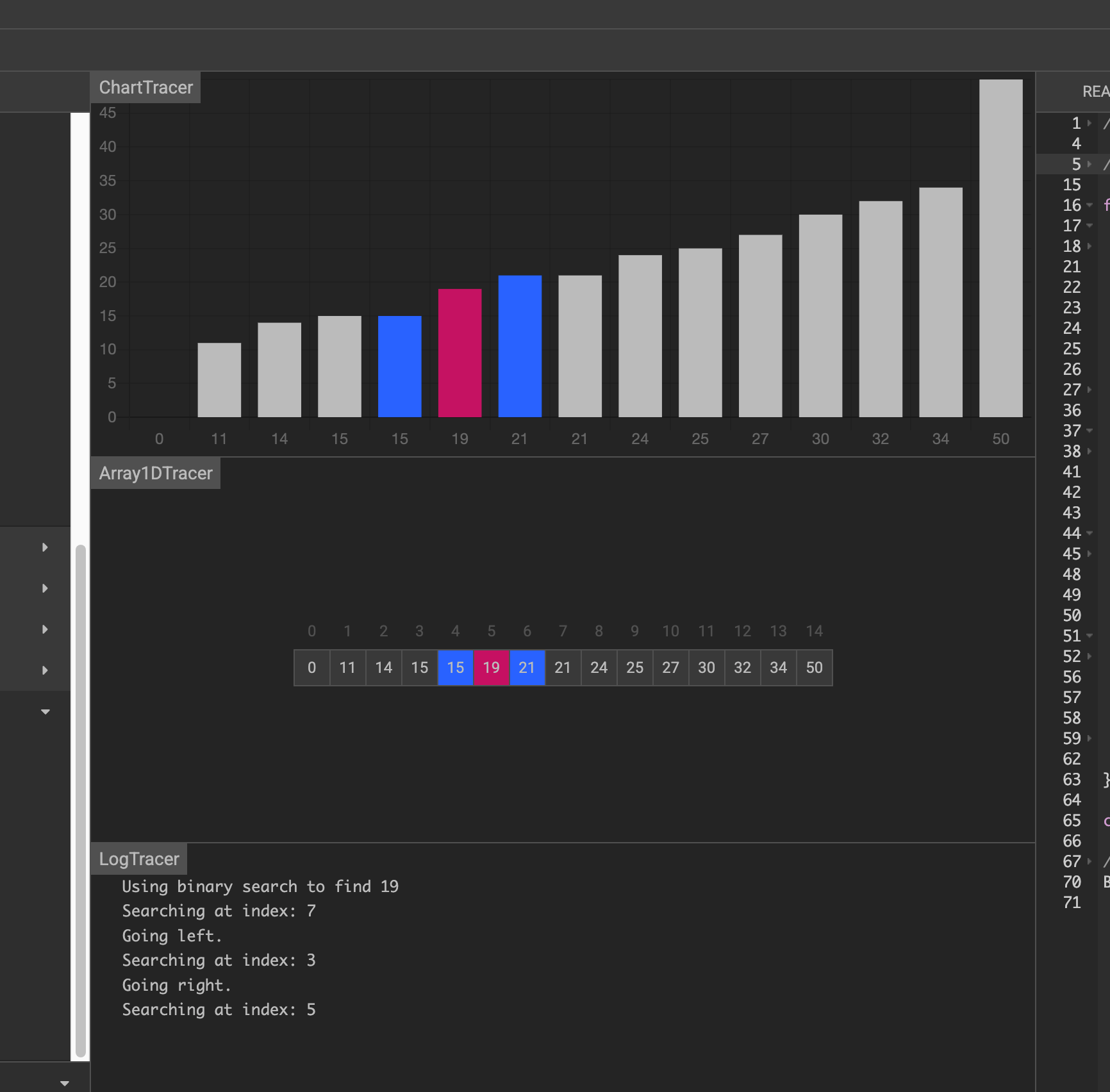
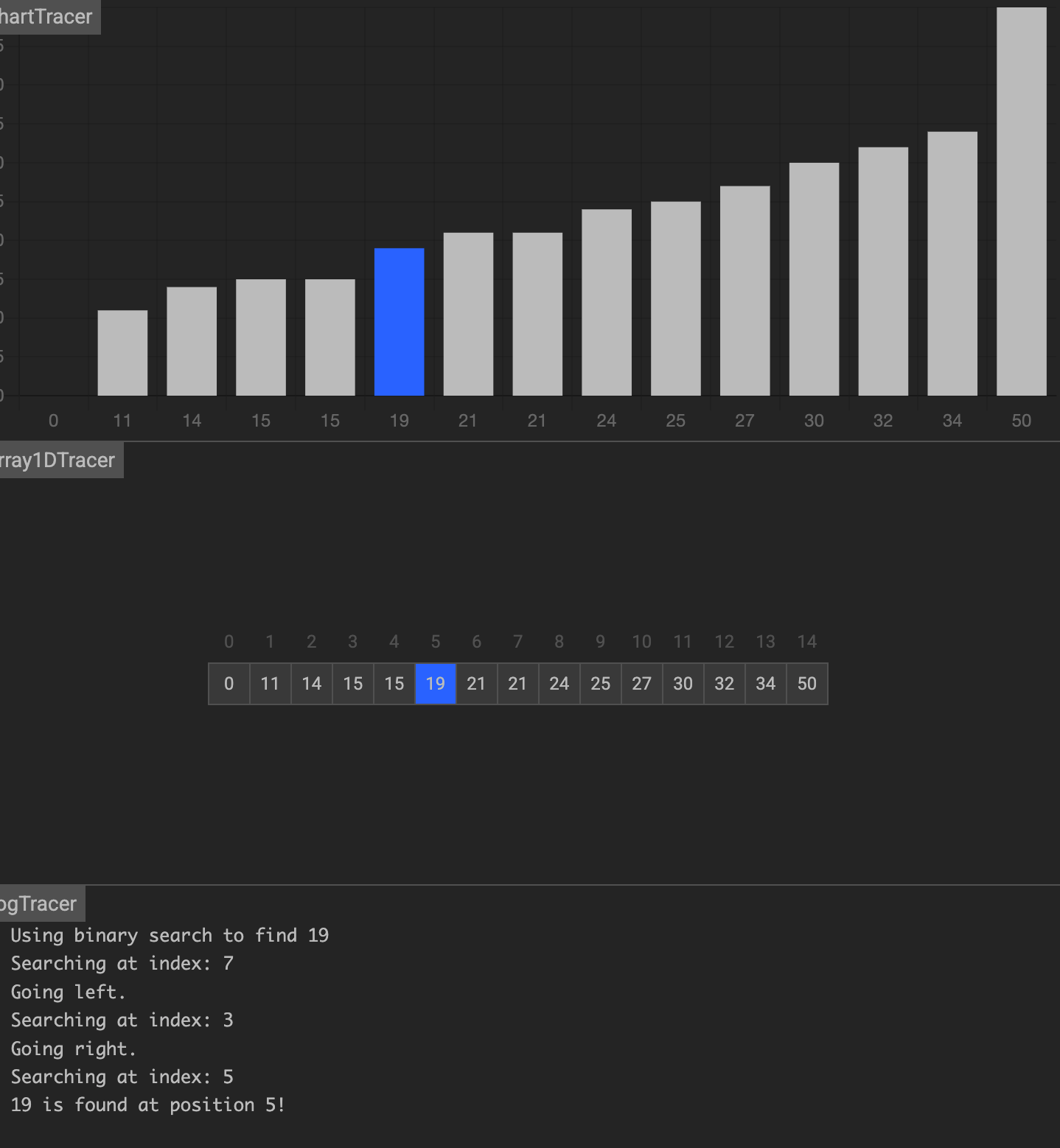
二分算法的复杂度:
| 复杂度类型 | 迭代实现 | 递归实现 |
|---|---|---|
| 时间复杂度 | O(log n) | O(log n) |
| 空间复杂度 | O(1) | O(log n) |
二叉查找树
二叉查找树是将一组无序的数据构造成一颗有序的树,设计思想与二分查找的设计思想类似。
二叉查找树:每个节点最多有两个子节点(二叉树);每个节点都大于自己的左孩子,同时小于自己的右孩子(有序)
假设要在下面的数据中找到指定元素
首先将这些数据按照二叉查找树的规则构建树
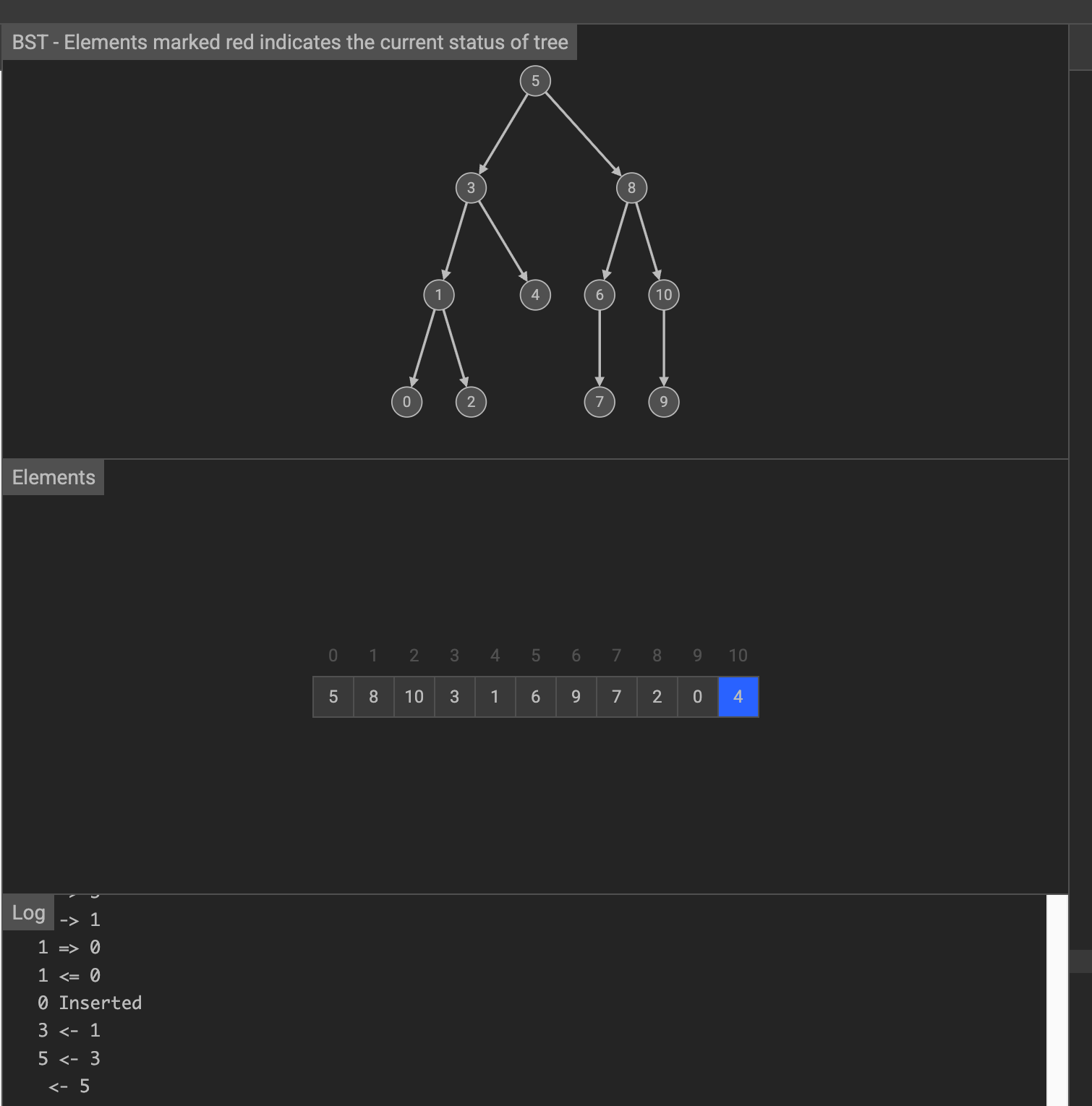
假设我们要搜索元素4,在顺序查找中,需要从第一个元素遍历到最后一个元素,才能找到。
即使使用二分查找,也需要先做一次排序,在进行查找,而排序则需要更多的资源。
使用二叉查找树,虽然也需要做一次排序,但是树和数组在排序好后,增加修改和删除元素的代价相比,树更低。
搜索的成本相同。
查找:
| 数据结构 | 查找时间复杂度 | 前提条件 |
|---|---|---|
| 有序数组 | O(log n) | 数组必须有序 |
| 二叉搜索树 | O(log n) | 树必须平衡 |
维护:
| 操作 | 有序数组 | 二叉搜索树 | 差异倍数 |
|---|---|---|---|
| 查找 | O(log n) | O(log n) | 1:1 |
| 插入 | O(n) | O(log n) | n:log n |
| 删除 | O(n) | O(log n) | n:log n |
| 空间开销 | O(n) | O(n) | 数组更紧凑 |
需要注意的是,二叉查找树可能面临退化
比如[3,2,1,5,6,7,9]
按照上述规则构建二叉查找树
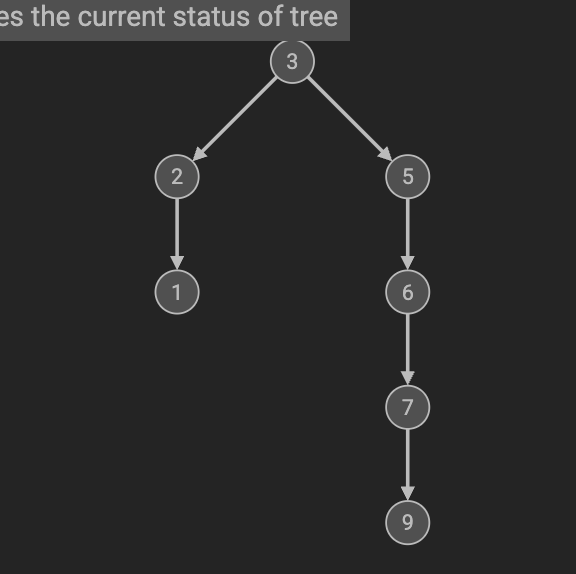
退化为二分查找的了。
同时如果元素可重复的话:
平衡二叉树
平成二叉树是二叉查找树的改进版,除了要满足二叉查找树的定义,还必须满足任意节点的平衡因子(两颗子树的高度差)的绝对值最大为1.
比如上面的二叉查找树,存在很明显的,右子树比较长,查找起来就需要比较更多的元素。甚至退化为顺序查找。
而平衡二叉树会对长的子树进行重新设置,控制整体平衡因子
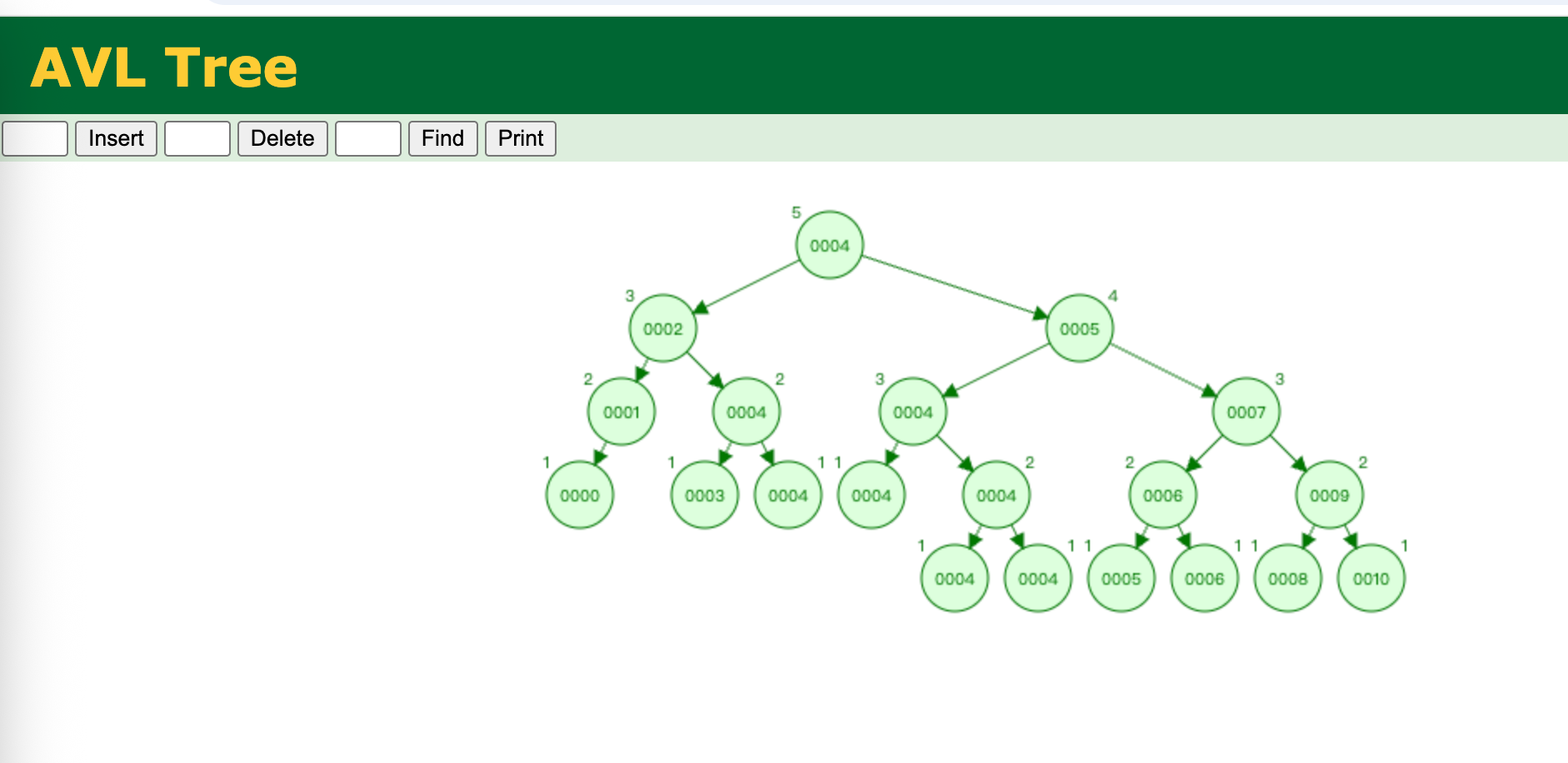
即使这颗树中,存在大量的重复元素4,但是其整体高度以及子树之间的差距比较小。
比如查找8元素
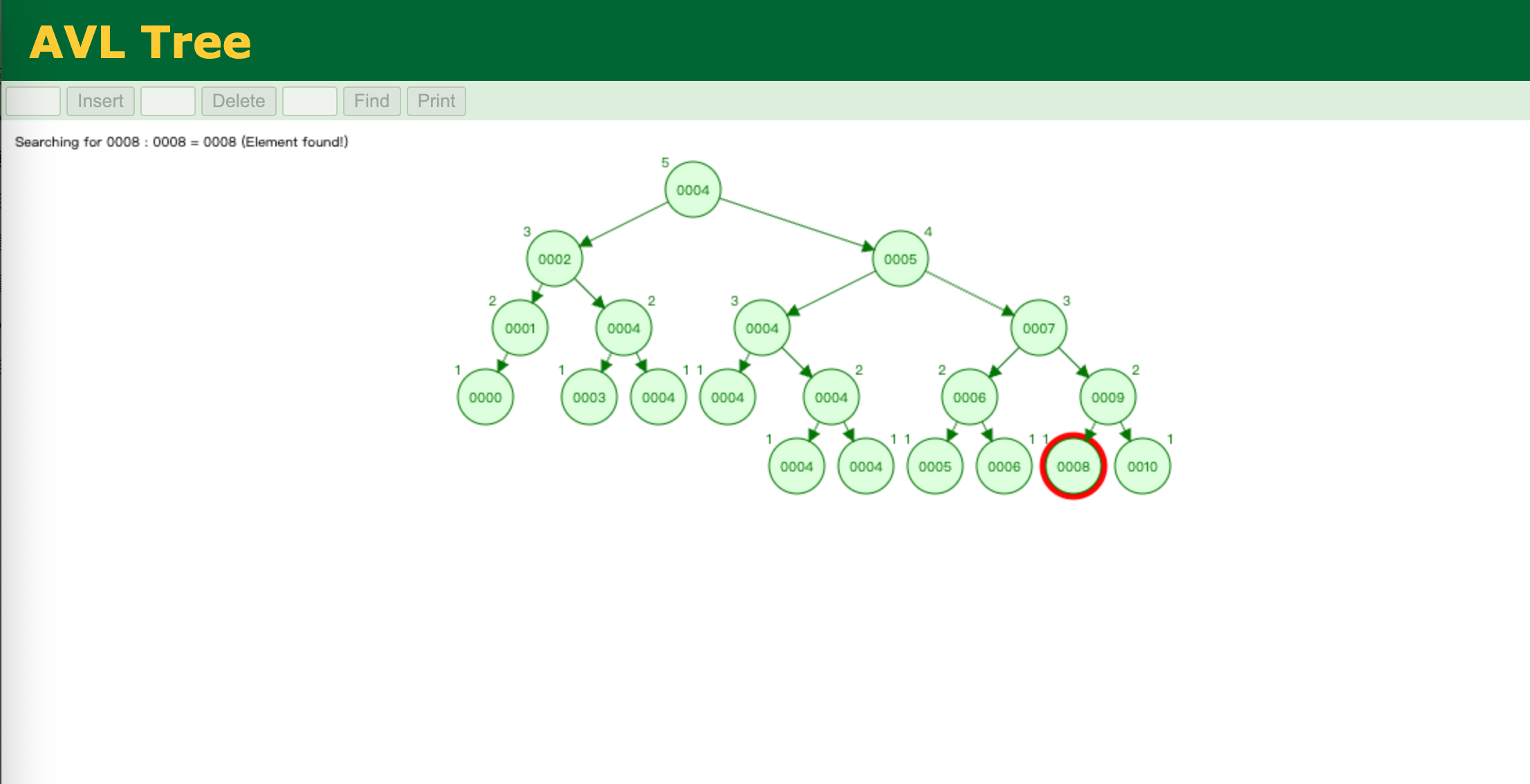
只需要比较5次
不同平衡树的成本对比
| 平衡树类型 | 查找成本 | 插入成本 | 删除成本 | 旋转复杂度 | 平衡标准 |
|---|---|---|---|---|---|
| AVL树 | O(log n) | O(log n) | O(log n) | 严格,最多2次旋转 | 高度平衡(严格) |
| 红黑树 | O(log n) | O(log n) | O(log n) | 宽松,最多3次旋转 | 颜色约束(宽松) |
| B树 | O(log n) | O(log n) | O(log n) | 节点分裂/合并 | 节点最小度数 |
| 伸展树 | O(log n) 均摊 | O(log n) 均摊 | O(log n) 均摊 | 无显式平衡操作 | 访问频率 |
B 树
B树是平衡二叉树的扩展,也是一棵平衡树,但是是多叉的,不是二叉的。
B树的特点:每个节点都存储了真实的数据;B树的查询效率与键在B树中的位置有关,最大时间复杂度与B+树(数据在叶子节点上)相同,最小时间复杂度为1(数据在根节点)
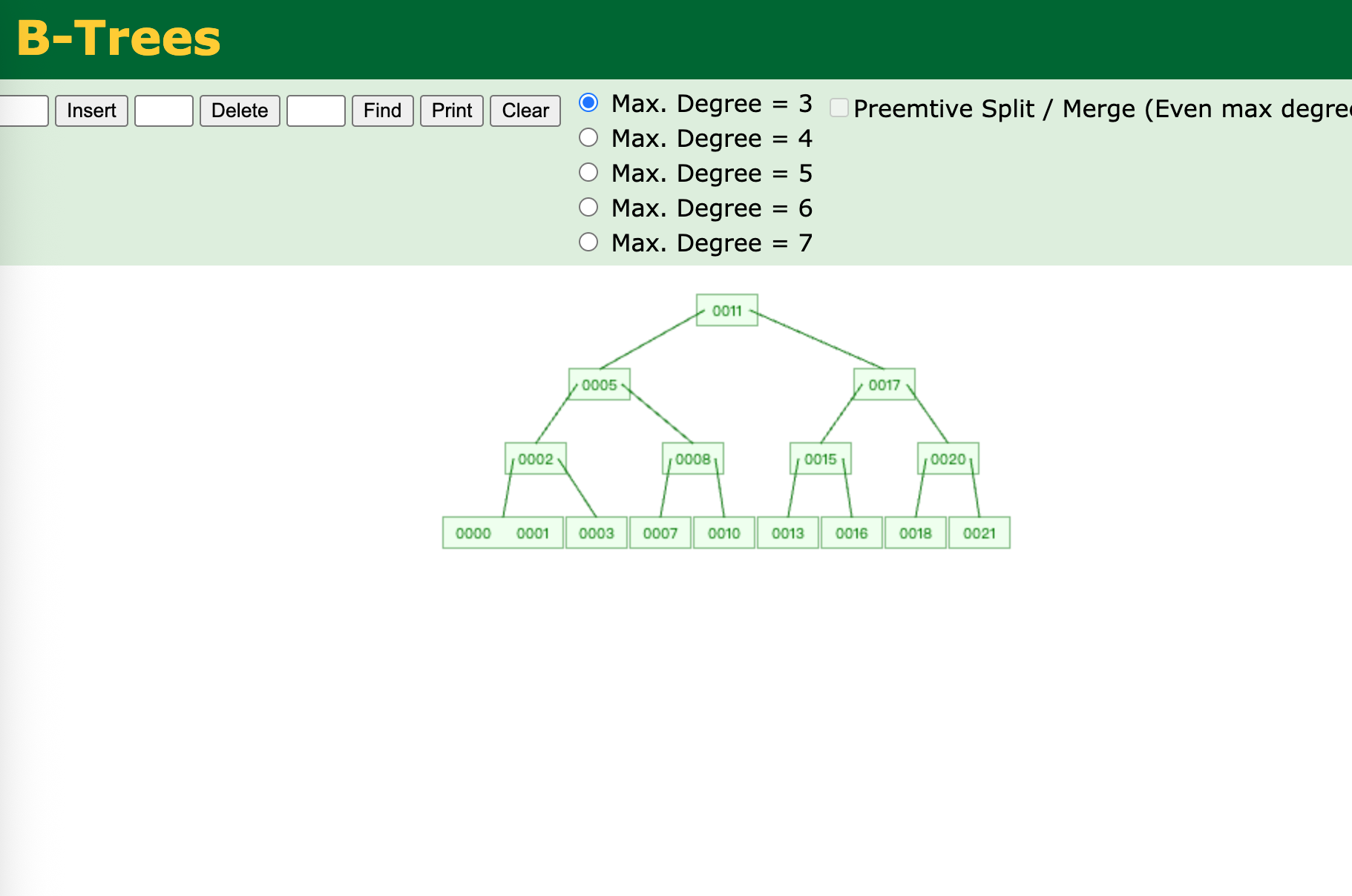
如果有重复元素
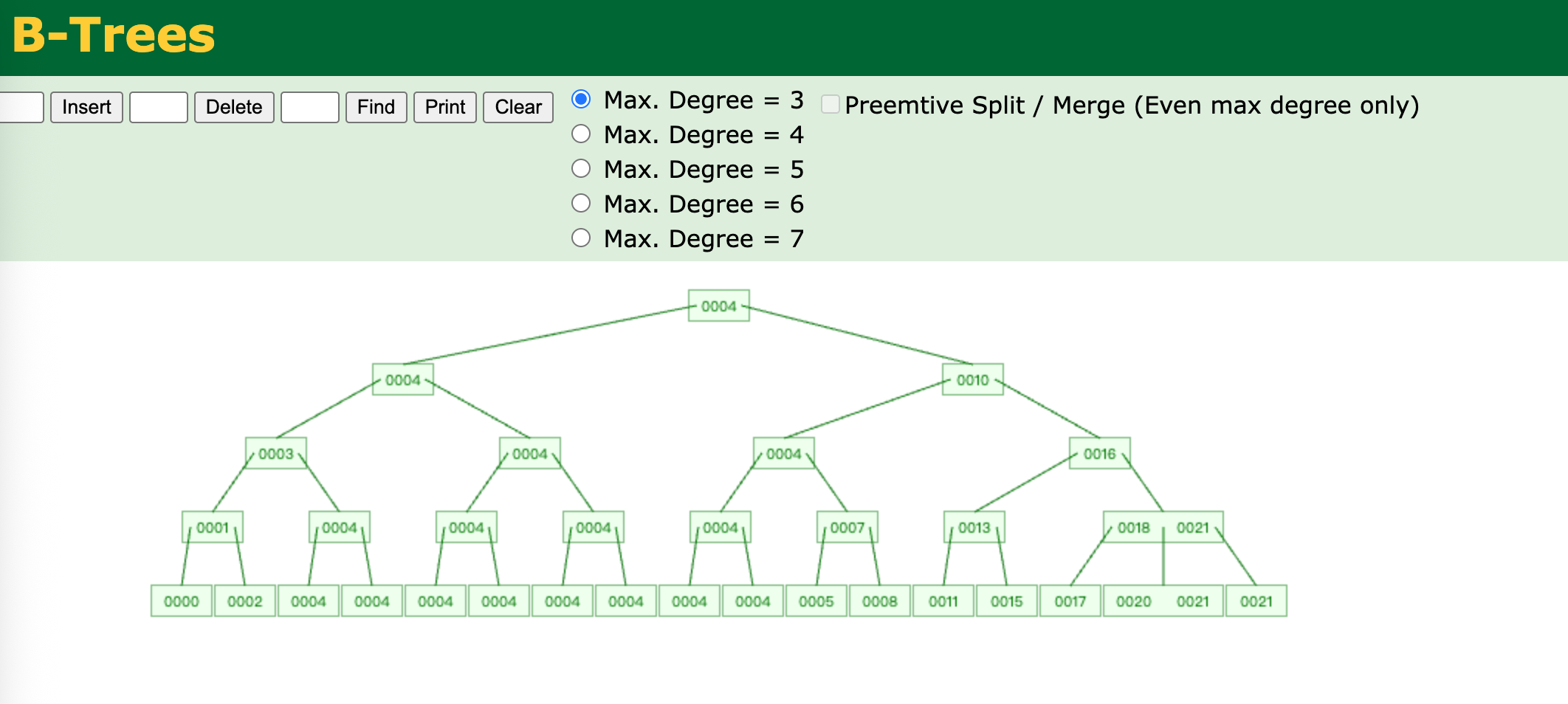
假设最大孩子树为3,那么每个节点最多可以存储2个元素值,而孩子则位于两个元素的三个位置。
查找
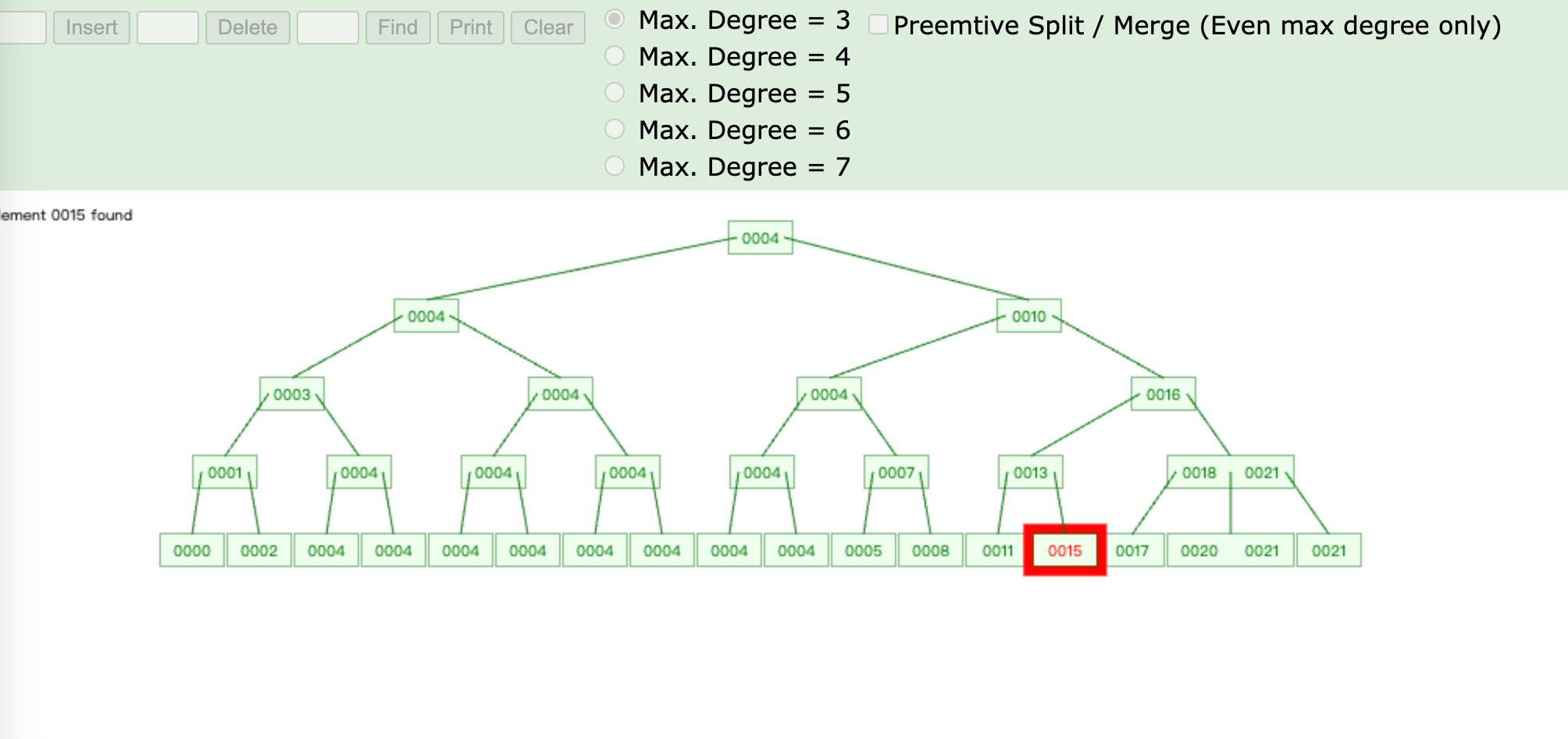
B+树
B+树是B树的变体,其定义与B树的定义基本一致。与B树相比,B+树的不同点如下:
- B+树的键都出现在叶子节点上,可能在内节点上重复出现
- B+树的内节点存储的都是键值,简直对应的具体数字都存储在叶子节点上。
- B+树比B树占的空间更多,因为B+树的叶子节点包括所有数据,而B树是整颗树包含所有数据。多处的部分就是B+树的内节点,但是B+树的内节点具有索引的作用,B+树的查询效率更高。
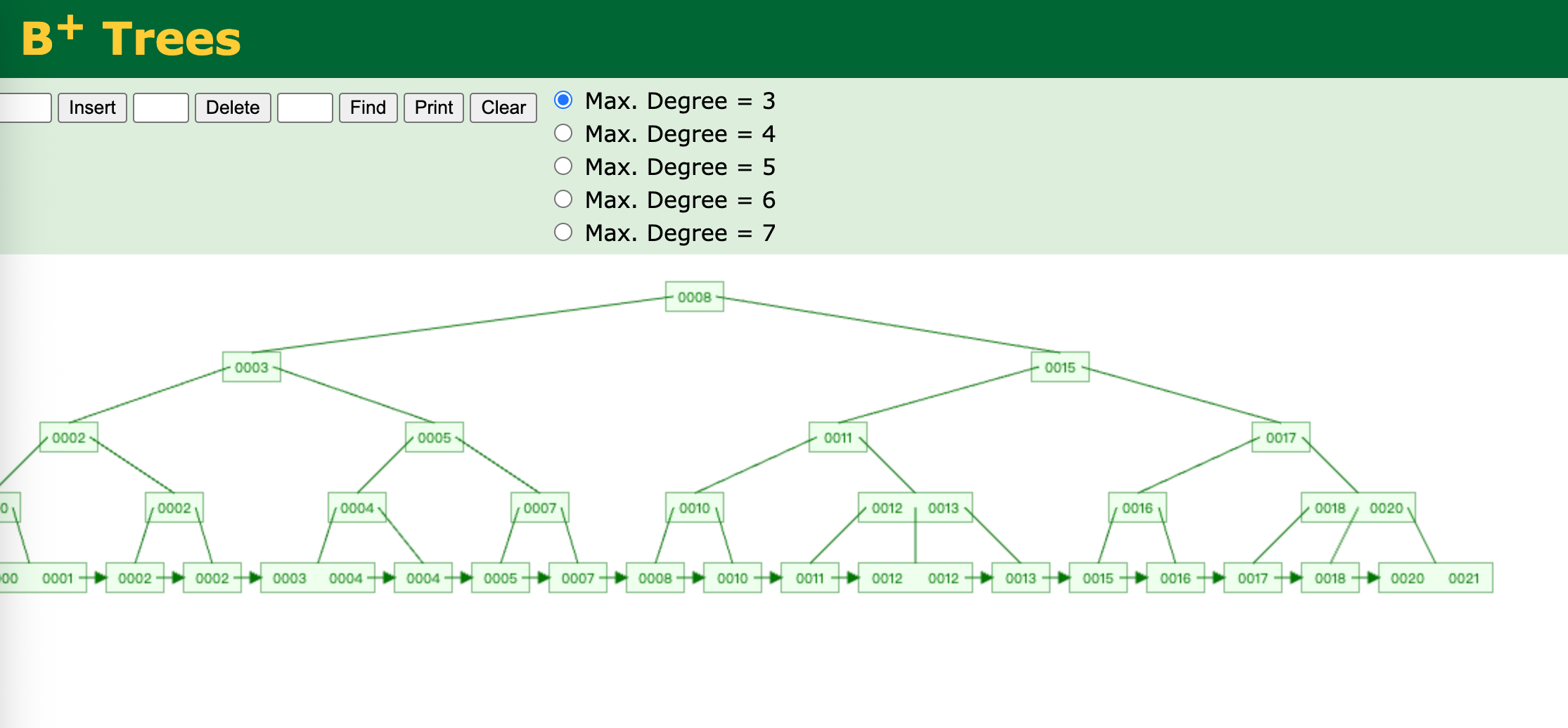
查找
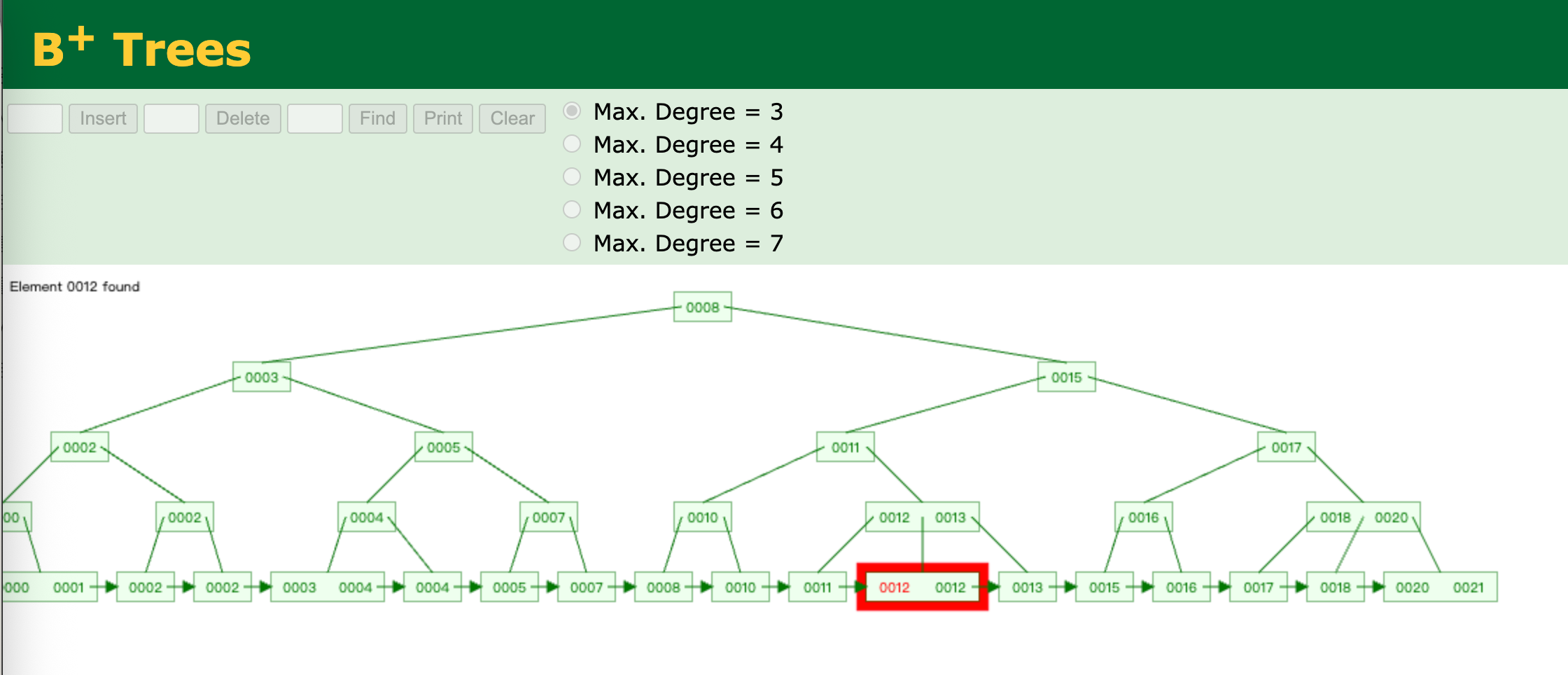
个人理解:B树针对单个元素的查找已经非常的快了,而且基本上是稳定的。
但是MySQL有范围查询,如果范围比较大,基本上需要将树遍历很多次,这个性能影响就很大了。
而B+树的叶子节点,也是一个顺序列表,如果是范围查询,那么只需要找到边界值即可,剩余元素就可以直接读取,不需要在从根节点查询了。
B+ 树索引
B+树索引就是基于B+树发展而来的,通常在 InnoDB上对某个字段添加索引,就是对这个字段构建一棵B+树。当查询条件是该索引字段时,查询速度非常快,对比逐行扫描,性能非常明显。
