[Metrics] RMSE vs ADE

RMSE and ADE sound similar, but they capture slightly different things about trajectory prediction quality.

Let’s break it down in a trajectory context:

1️⃣ RMSE (Root Mean Squared Error)

• Formula (per trajectory):

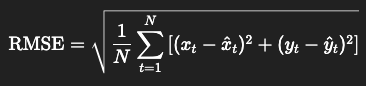
• You square the coordinate errors, average them, then take the square root.

• Sensitive to large errors because squaring amplifies outliers.

• Units: same as position (e.g., meters).

• Tends to penalize big mistakes more heavily — a single bad prediction can inflate RMSE a lot.

2️⃣ ADE (Average Displacement Error)

• Formula (per trajectory):
  

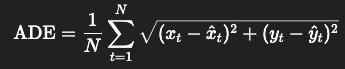
• You compute the Euclidean (L2) distance at each timestep, then average.

• Every timestep is weighted equally.

• More interpretable: “average meters off” per prediction step.

• Less punishing for occasional big misses — focuses on typical step error.

🚗 Why both are used in trajectory prediction

• ADE tells you the average positional accuracy — how far off you are most of the time.

• RMSE tells you about consistency — whether you sometimes make very large mistakes.

• A model can have low ADE but high RMSE if it’s usually accurate but occasionally very wrong.

• A model can have low RMSE but high ADE if it’s consistently a bit off, but never drastically.

Quick intuition example:

Prediction error over 3 timesteps	ADE	RMSE
[1m, 1m, 1m]	1.0	1.0
[0.5m, 0.5m, 2.5m]	1.17	1.46 (big miss amplified)

So in research & benchmarks, ADE gives the “how far on average” view, while RMSE shows how bad your worst moments hurt your performance.