当前位置：首页 > news >正文

深度学习周报（8.4~8.10）

news 2025/8/11 7:46:43

摘要

Abstract

1 PCA实践

1.1 原数据

1.2 降维后数据

2 其他的降维算法

3 异常检测

3.1 高斯分布

3.2 算法

3.3 评估

4 总结

摘要

本周首先进行了PCA降维的实战训练，对比了降维前后的数据散点图。其次，了解了其他的降维算法，如t-SNE和LLE等，学习了它们的原理与优缺点。最后，认识了异常检测的概念与应用，在回顾正态分布的基础上学习了异常检测算法的推导过程，了解了它的评估方法以及与监督学习的不同之处。

Abstract

This week, we first conducted practical training on PCA dimensionality reduction, comparing scatter plots of the data before and after dimensionality reduction. Next, we explored other dimensionality reduction algorithms, such as t-SNE and LLE, studying their principles, advantages, and disadvantages. Finally, we were introduced to the concept and applications of anomaly detection. Building upon a review of the normal distribution, we learned the derivation process of anomaly detection algorithms, and understood their evaluation methods and the differences between anomaly detection and supervised learning.

1 PCA实践

本次实践主要也是利用前面的鸢尾花数据集，根据花萼长度、花萼宽度，花瓣长度与花瓣宽度四个特征将鸢尾花分为三类。

1.1 原数据

数据示例如下：

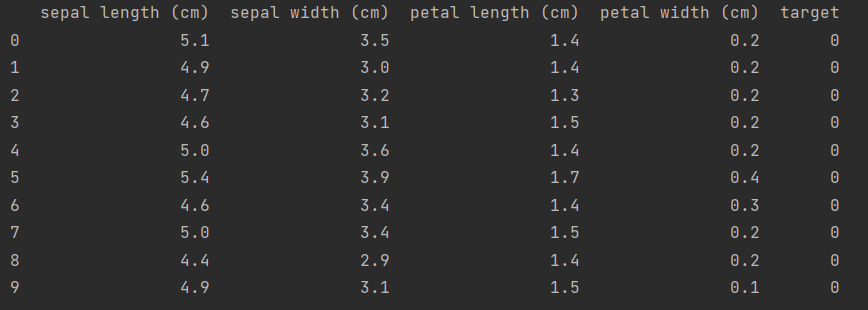
根据其前三个特征绘制散点图，代码如下：

#加载数据集
iris = load_iris()
X = iris.data
Y = iris.target#创建一个图像窗口，尺寸为(8, 8)
fig = plt.figure(figsize=(8, 8))
#在窗口中添加一个子图（subplot），并指定为三维坐标系；111表示1行1列1个子图
ax = fig.add_subplot(111, projection='3d')#针对每一类别绘制散点图
for c, i, target_name in zip(['blue', 'red', 'green'], [0, 1, 2], iris.target_names):ax.scatter(X[Y == i, 0], X[Y == i, 1], X[Y == i, 2], color=c, label=target_name)

上述代码中，循环部分使用 zip() 同时遍历三个列表：

1.颜色列表：['blue', 'red', 'green']，分别给三个类别上色

2.类别索引：[0, 1, 2]，对应三种鸢尾花的标签值

3.类别名称：iris.target_names，即['setosa', 'versicolor', 'virginica']

每次循环取出一组对应，如：('blue', 0, 'setosa')

可得到散点图如下：

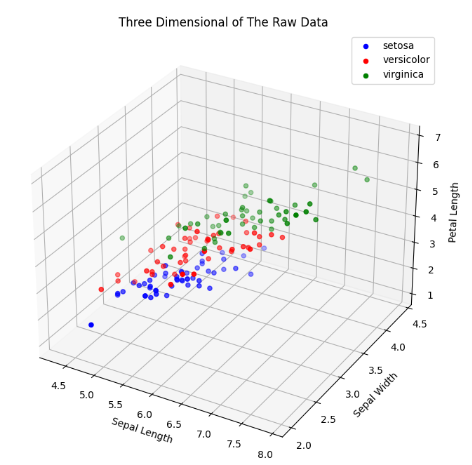
1.2 降维后数据

利用PCA降维的代码如下：

class PCA():#计算协方差矩阵def calculate_covariance_matrix(self, X, Y=None):m = X.shape[0]   #样本数量X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)    #对数据集X的每个特征进行标准化#若Y=None则计算X自身的协方差，否则对Y进行标准化if Y == None:Y = Xelse:Y = (Y- np.mean(Y, axis=0)) / np.std(X, axis=0)#计算并返回协方差矩阵return 1 / m * np.matmul(X.T, Y)#将n维数据降维成n_components维数据def transform(self, X, n_components):covariance_matrix = self.calculate_covariance_matrix(X)#获取特征值与特征向量（np.linalg.eig()对一个方阵进行特征分解）values, vectors = np.linalg.eig(covariance_matrix)#排序，选取最大的前n_components组idx = values.argsort()[::-1]     # 获取特征值降序排列的索引vectors = vectors[:, idx]        # 按重要性重排序特征向量vectors = vectors[:, :n_components]       # 保留前n_components个主成分return np.matmul(X, vectors)#降成3维数据
X_pca = PCA().transform(X, 3)

降维后的散点图如下：

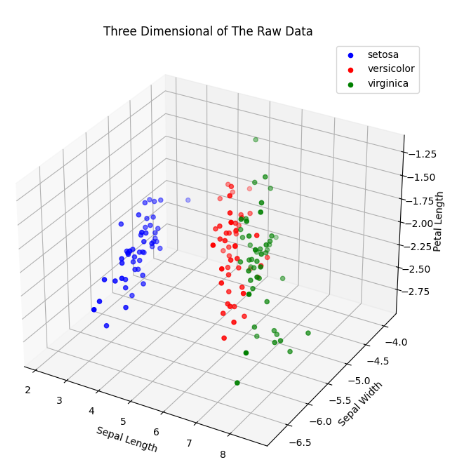
计算解释方差比例和累计解释方差比例的代码如下：

#计算解释方差比例
total_variance = np.sum(values)
explained_variance_ratio = values / total_variance#计算累计解释方差比例（np.cumsum()用于累积求和）
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)

得到的解释方差比例为 $\begin{bmatrix} 0.7296 &0.2285 & 0.0367 & 0.0052 \end{bmatrix}$ ，前三个维度的累计解释方差比例为 $0.9948$ 。

2 其他的降维算法

除了PCA以外，其他常见的降维算法还有如下几种：

1.t-SNE，通过将高维空间中的距离转换为概率分布来衡量点与点之间的相似性，并试图在低维空间中找到一种表示方式，使得这种相似性尽可能地被保留下来。这种方法适合探索数据的局部结构和进行可视化，尤其是对于数据集中的聚类。但它的计算成本较高，结果难以解释，也不保证全局结构的保真度。

2.LLE，首先确定每个点的邻居及权重（这些邻居及权重可以尽可能准确地重建该点），然后在保持权重不变的情况下，在低维空间中寻找一个相似的表示，使之能进行相似的重构。这种方法也能保留数据的局部结构，且更加直观，容易理解，但它对于参数和噪声都比较敏感，难以处理新的测试数据。

3.自编码器（Autoencoder），是一种基于神经网络的降维方法，通常由编码器和解码器两部分构成。先通过编码器将输入数据压缩到一个低维空间，再通过解码器尝试从这个低维表示重建原始输入。它可以学习到非常复杂的映射关系，灵活，可扩展，但需要大量的数据和计算资源进行训练，模型架构的选择也可能会影响性能。

4.isomap，是一种用于降维的非线性方法，首先为每个数据点找到其最近邻点，并基于这些邻近关系构建一个加权图，然后基于图计算每对点之间的最短路径距离，最后采用经典多维缩放技术，将这些测地距离映射到一个低维空间中。它相比于LLE与t-SNE更注重全局结构，适用范围也比较广，但它计算复杂度很高，也同样对噪声敏感。

3 异常检测

异常检测，是指识别数据中与正常模式显著不同的罕见项、事件或观测值的过程，是机器学习算法的一个常见应用。虽然它主要用在无监督学习问题，但从某些角度看，跟监督学习问题很相似。

异常检测主要是对给定的无标签训练集的分布概率进行建模，然后判断新样本的概率是否低于设定的阈值，若低于则标记为异常。它的主要应用包括识别异常用户、在工业制造领域进行设备的故障预测，数据中心计算机的运维监控等等。

3.1 高斯分布

高斯分布也叫正态分布，它的表示方式如下：

$X\sim N(\mu ,\sigma^{2} )$

其中 $\mu$ 为均值，决定了分布的中心位置； $\sigma$ 为标准差，决定了分布的宽窄。

其变化过程可能如下所示：

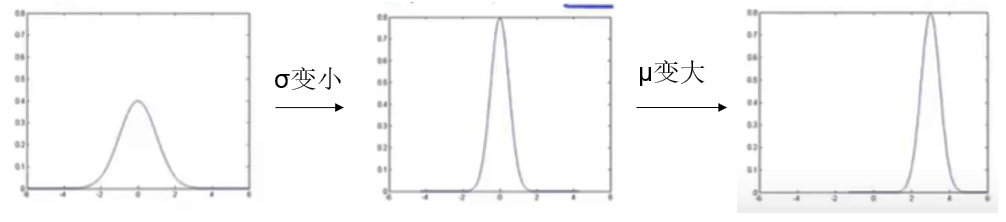
其公式如下：

$p(x;\mu ,\sigma^{2} ) = \frac{1}{\sqrt{2\pi }\sigma} exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})$

3.2 算法

假设对于每个样本，其n个特征（相互独立）服从高斯分布，即：

$\begin{matrix} \\ \\ \\ \\ \end{matrix}$ $\begin{matrix} x_{1}\sim N(\mu_{1} ,\sigma^{2}_{1} )\\ x_{2}\sim N(\mu _{2},\sigma^{2}_{2} )\\ x_{3}\sim N(\mu_{3} ,\sigma^{2}_{3} )\\ ...\\ x_{n}\sim N(\mu_{n} ,\sigma^{2} _{n}) \end{matrix}$

那么可以计算每个样本点的联合概率密度如下：

$p(x) = p(x_{1};\mu_{1} ,\sigma^{2}_{1} )p(x_{2};\mu_{2} ,\sigma^{2}_{2} )p(x_{3};\mu_{3} ,\sigma^{2}_{3} )...p(x_{n};\mu_{n} ,\sigma^{2}_{n} )$

即： $p(x) = \prod_{j =1}^{n}p(x_{j};\mu_{j} ,\sigma^{2}_{j} )$

那么，在高斯分布的基础上进行异常检测算法的推导，过程大致如下：

首先，选择一些特征以指出异常样本。当出现异常样本时，这些特征的特征值会特别大或特别小。可以通过错误检测，即观察出错样本，来判断是否需要增加新的特征进行特征的选择。

其次，对这些特征的特征值计算均值与方差，公式如下（m为样本数量）：

$\mu_{j} = \frac{1}{m} \sum_{i=1}^{m}x_{j}^{(i)}$

$\sigma_{j}^{2} = \frac{1}{m} \sum_{i=1}^{m}(x_{j}^{(i)}-\mu_{j})^{2}$

最后，对于给定的新样本，计算其概率，公式和上面计算每个样本点联合概率密度的公式一样，不过 $\mu_{j}$ 和 $\sigma_{j}^{2}$ 由上一步得到， $x_{j}$ 则是新样本对应特征的特征值。如果计算出的概率小于阈值 $\varepsilon$ ，则说明该新样本为异常样本。

3.3 评估

为了评估一个异常检测算法，可以使用少量带标签的数据（通常将它们划分到交叉验证集与测试集中）。

首先，使用训练集拟合模型 $p(x)$ ，如前两节，把m个无标签样本用高斯函数进行拟合（虽然称为无标签，但实际上假设它们均为正常样本）。

然后，对交叉验证集和测试集中的样本进行预测。

$y = \left\{\begin{matrix} 1 &\; \;\;if \:\: p(x)<\varepsilon(anomaly) \\ 0 &\; if\: \: p(x)\geq \varepsilon(normal) \end{matrix}\right.$

最后，对于参数 $\varepsilon$ ，即阈值，可以使用交叉验证集进行选择，比如最大化F1分数。

在上述第二步，可以把异常检测算法看成是对交叉验证集与测试集中的y标签进行预测，这就和监督学习非常相似，只不过正常样本（y = 0）会比异常样本（y = 1）更加常见。这种情况在前面的学习中有所提及，此时采用分类正确率进行评估可能不准，可以采用查准率、召回率或者F1分数来总结和反映精度。

同时由上可得，在正常样本很多、异常样本很少的情况下通常采用异常检测算法；而在合理范围内正常样本和异常样本差不多的情况下通常采用监督学习算法。异常检测时，经常有许多不同类型的异常，很难从正样本中学习异常是什么；而监督学习算法有足够数量的正样本来训练识别它们的算法，需要识别的样本与当前训练集中的样本可能是类似的。

4 总结

本周通过对PCA的代码训练，对PCA有了更加清晰的认识，并且总结了其他常见的降维算法。除此之外，对异常检测算法进行了初步的了解，学习了其概念、算法与评估等知识点。下周考虑深入学习多变量的异常检测（事实上，本周的算法推导也是多变量，只不过加了一个特征相互独立的前提，将一个多变量问题变成了n个单变量问题，参数估计方式也只针对单个特征）。

查看全文

http://www.dtcms.com/a/324433.html