【CF】Day118——杂题 (随机哈希 / 思维 | 贪心 / DP | 位运算构造 | 状态压缩 + 建图 + 最短路 | 构造 | 贪心)
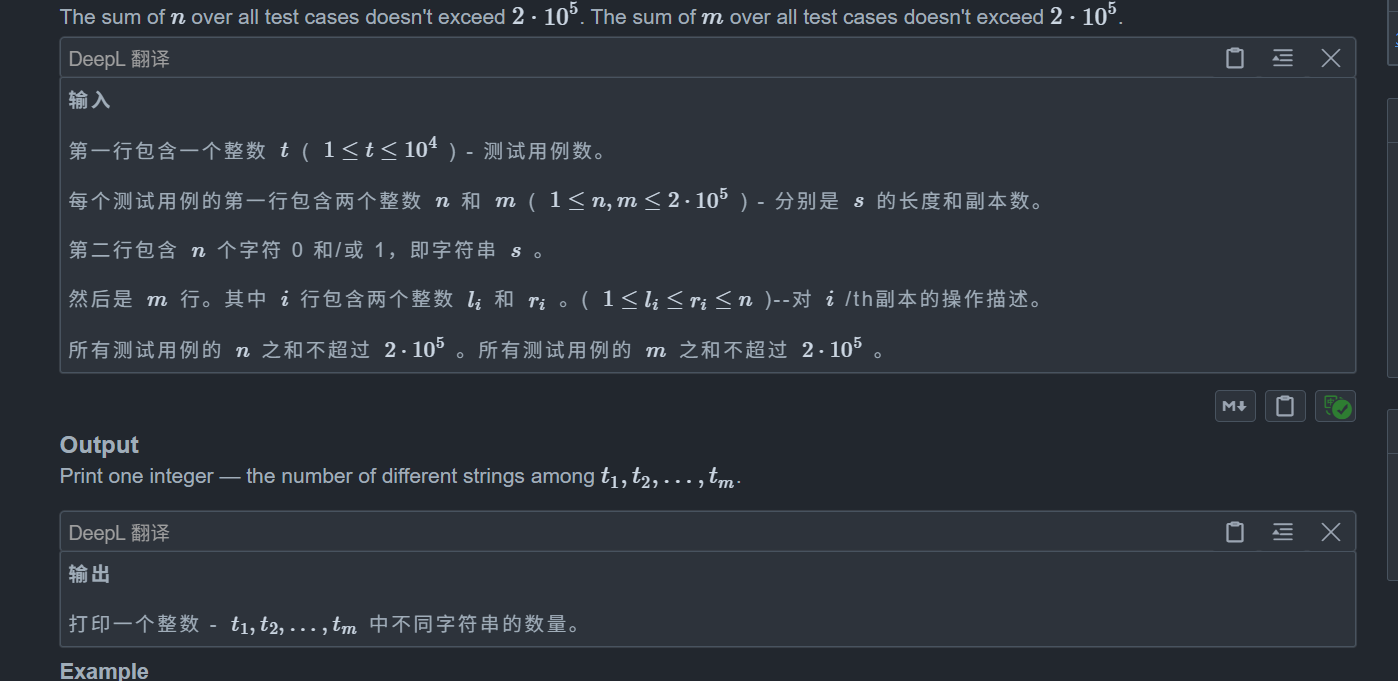
C. Binary String Copying
题目:
 思路:
思路:
随机哈希 / 思维
对于区间字符串,不难想到字符串哈希,这里我们采用随机哈希,每一位的基数都不一样,其余操作都和正常哈希差不多,唯一注意点就是我们还要构造一个全 1 的哈希,因为排序后我们是一串连续 1,提前处理方便查询
另一种方法很巧妙,我们发现排序后我们 0 在左 1 在右,因此不难想到我们可以考虑只记录有效的部分,如 0001100111,我们对这个排序其实只是对 1100 排序,所以我们可以找到区间左端点往右的第一个 1,区间右端点往左的第一个 0,而新的 l , r 才是真正有效的修改区间,我们用一个 map 记录即可
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"int h[200005];
int sumone[200005];
int hone[200005];std::vector<int> base;std::mt19937_64 rnd(time(0));void get_hash(int n) {base.assign(n+1, 0);for (int& i : base) i = rnd();
}void solve()
{int n,m;cin >> n >> m;get_hash(n);string s;cin >> s;s = ' ' + s;set<int> haxi;for (int i = 1; i <= n; i++) {sumone[i] = sumone[i-1] + s[i] - '0';hone[i] = hone[i-1] + base[i];}for (int i = 1; i <= n; i++){h[i] = h[i-1] + ((s[i] == '1') ? base[i] : 0);}while(m--){int l,r;cin >> l >> r;int old = h[n] - h[r] + h[l-1];int cnt = sumone[r] - sumone[l-1];int cur = hone[r] - hone[r - cnt];haxi.insert(old + cur);}cout << (int)haxi.size() << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
int l[200005],r[200005];
void solve()
{int n,m;cin >> n >> m;string s;cin >> s;s = ' ' + s;int pos = 0;for (int i = 1; i <= n; i++){if(s[i] == '0')pos = i;l[i] = pos;}pos = n+1;for (int i = n; i >= 1; i--){if(s[i] == '1')pos = i;r[i] = pos;}map<pair<int,int>,bool> mp;while(m--){int a,b;cin >> a >> b;a = r[a];//往右走到第一个 1b = l[b];//往左走到第一个 0if(a > b){a = 1,b = 1;}mp[make_pair(a,b)] = true;}cout << mp.size() << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}D. Array Painting
题目: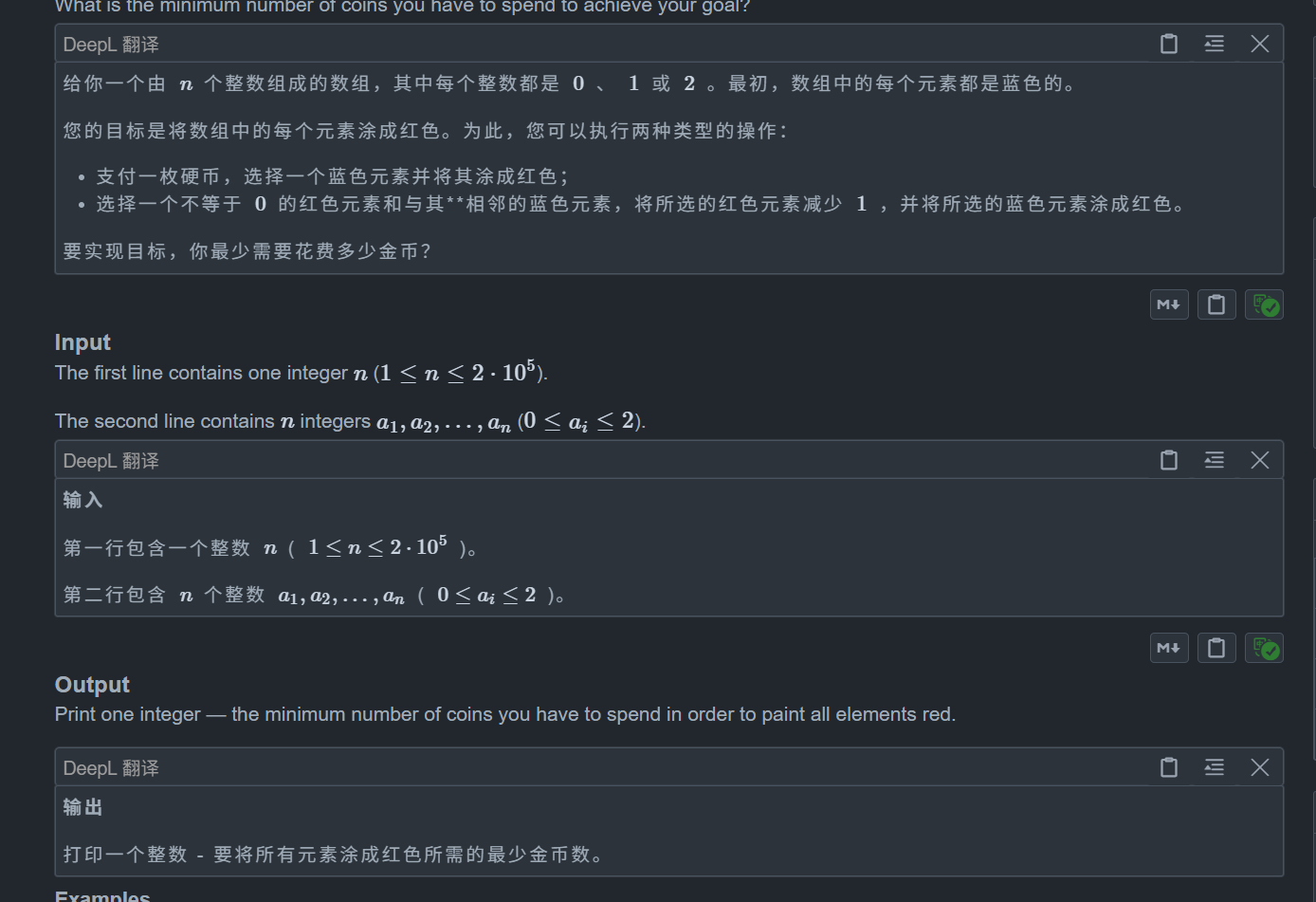
思路:
贪心 / DP
不难想到贪心做法,对于一个全大于 0 的区间,我们只需要一个金币就能一网打尽,甚至还能多一个,而如果其中还有 2,那么就能多两个
不过这样显然有点麻烦了,我们不妨直接从左往右模拟即可,如果当前前后可能有 1 or 2,那么就使用他们,否则就说明他是一个孤立点,所以就要消费了
还有另外一种DP做法,我们定义 dp[i][j] 为 解决前 i 个,且最后一个是数字 j 的最小花费
那么显然对于 dp[i][a[i]] 可以从前面转移,即从 1 或者 2 转移,如果前面是 0,那么就自费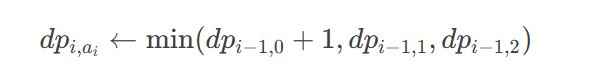
当然,这种情况是依赖于前面已经解决的,我们也可以先解决自身,然后看看能不能由 i 往前转移,显然转移位置就是 i 往左第一个 0 的位置,则有
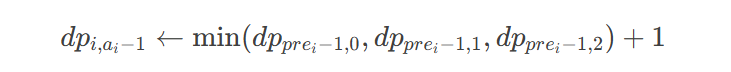
即消耗自身,然后解决一段连续的正区间 + 一个 0,然后自身少一(往左转移了)
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"int n;
int a[200005];
int vis[200005];
vector<vector<int>> pos(3);
int ans = 0;
void solve()
{cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 1; i <= n; i++){if (i > 1 && a[i - 1]){a[i - 1]--;}else if (a[i] == 0 && i < n && a[i + 1]){a[i + 1]--;}else{ans++;}}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"int n;
int a[200005];
int pre[200005];
int dp[200005][3];
int ans = 0;
void solve()
{memset(dp, 0x3f, sizeof dp);dp[0][0] = dp[0][1] = dp[0][2] = 0;cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}dp[1][a[1]] = 1;for (int i = 1; i <= n; i++){pre[i] = a[i] ? pre[i - 1] : i;}for (int i = 2; i <= n; i++){dp[i][a[i]] = min({dp[i - 1][0] + 1, dp[i - 1][1], dp[i - 1][2]});if (a[i]){int last = pre[i] - 1;dp[i][a[i] - 1] = min({dp[last][0], dp[last][1], dp[last][2]}) + 1;}}cout << min({dp[n][0], dp[n][1], dp[n][2]}) << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
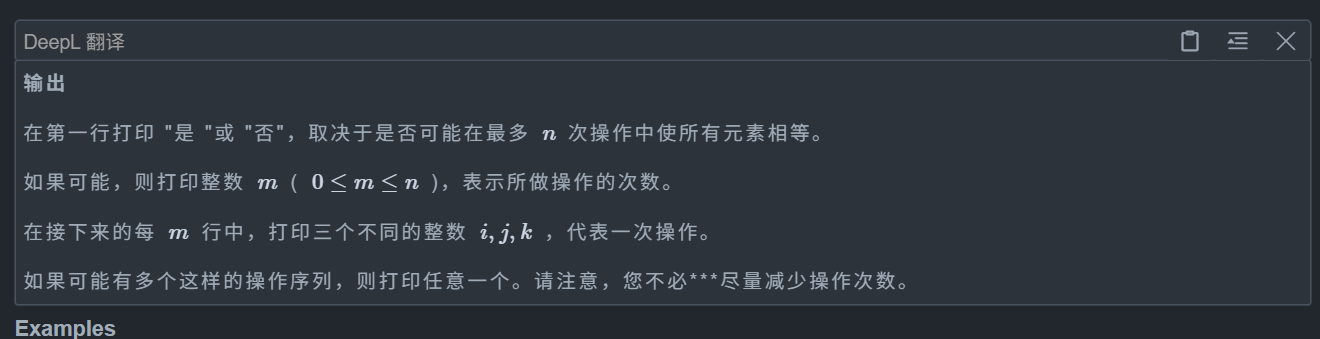
}D. Powerful Ksenia
题目: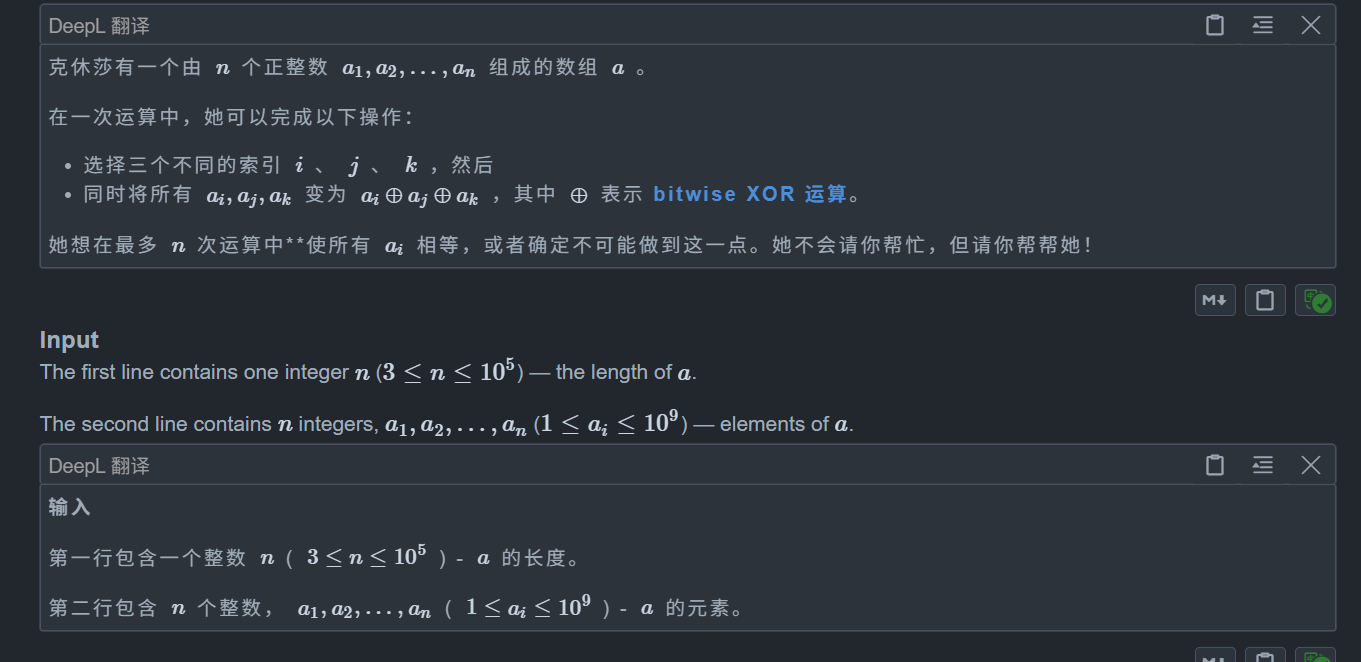
 思路:
思路:
位运算构造
不是很难的一题,但也有难度
对于奇数情况我们很简单能想到一个方法,如 a b c d e,我们可以先将 a b c 变成 x,即变成 x x x d e,然后变成 x x y y y,即再将三个数变成同一个数,注意到 a ^ a ^ b = b,所以我们可以选择 x x y 三个数异或,这样就都变成 y 了,总花费 n - 1 次
对于偶数情况,我们要观察到一个性质,即每次操作后整个数组的异或和是不会改变的,而最后的所有值相等,所以我们的异或和就是 0,所以此时的方法也很巧妙,如果我们先处理 n - 1 个数即按奇数情况处理,如果倒数第二个数不等于最后有一个数,那么此时显然就不可能构造,或者提前判断是不是异或和为 0
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"
int n;
int a[100005];
void solve()
{cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}if (n & 1){yes;cout << n - 1 << endl;for (int i = 1; i <= n - 2; i += 2){cout << i << " " << i + 1 << " " << i + 2 << endl;}for (int i = 1; i <= n - 2; i += 2){cout << i << " " << i + 1 << " " << n << endl;}}else{for (int i = 1; i <= n - 2; i += 2){a[i] = a[i + 1] = a[i + 2] = a[i] ^ a[i + 1] ^ a[i + 2];}if (a[n] != a[n - 1]){no;}else{yes;cout << n - 3 << endl;for (int i = 1; i <= n - 2; i += 2){cout << i << " " << i + 1 << " " << i + 2 << endl;}for (int i = 1; i <= n - 4; i += 2){cout << i << " " << i + 1 << " " << n << endl;}}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}G. Rudolf and CodeVid-23
题目:
思路:
状态压缩 + 建图 + 最短路
看到 n 为 10,不难想到状态压缩,我们利用二进制数表示是否含有某种病,那么我们考虑建图,一共最多 1024 种情况,即 1024 个点,两两有边,那么最多含有 1e6 条边,可行
而吃药天数相当于边的权值,吃完药后的状态就是子节点,没吃药时就是父节点,因此我们跑一个最短路即可
对于子节点如何计算,其实也很简单,消除状态其实就是对其取反后和父节点做异或,添加状态则是直接或运算即可
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"struct Node
{int day, z, d;
} node[1105];
int n, m;
int d;
string a, b, s;void solve()
{cin >> n >> m;cin >> s;vector<int> dis(1105, 0);vector<int> vis(1105, 0);for (int i = 0; i < (1 << n); i++){dis[i] = INT_MAX;}dis[stoi(s, nullptr, 2)] = 0;for (int i = 1; i <= m; i++){cin >> d >> a >> b;node[i].day = d;node[i].z = stoi(a, nullptr, 2);node[i].d = stoi(b, nullptr, 2);}while (true){int v = -1;for (int i = 0; i < (1 << n); i++){if (vis[i] || dis[i] == INT_MAX){continue;}if (v == -1 || dis[i] < dis[v]){v = i;}}if (v == -1){break;}vis[v] = 1;for (int i = 1; i <= m; i++){int w = node[i].day;//对 z 取反后和 状态 v 合并,最后加上新病状int u = (v & (((1 << n) - 1) ^ node[i].z)) | node[i].d;dis[u] = min(dis[u], dis[v] + w);}}cout << (dis[0] == INT_MAX ? -1 : dis[0]) << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}D. Row Major
题目: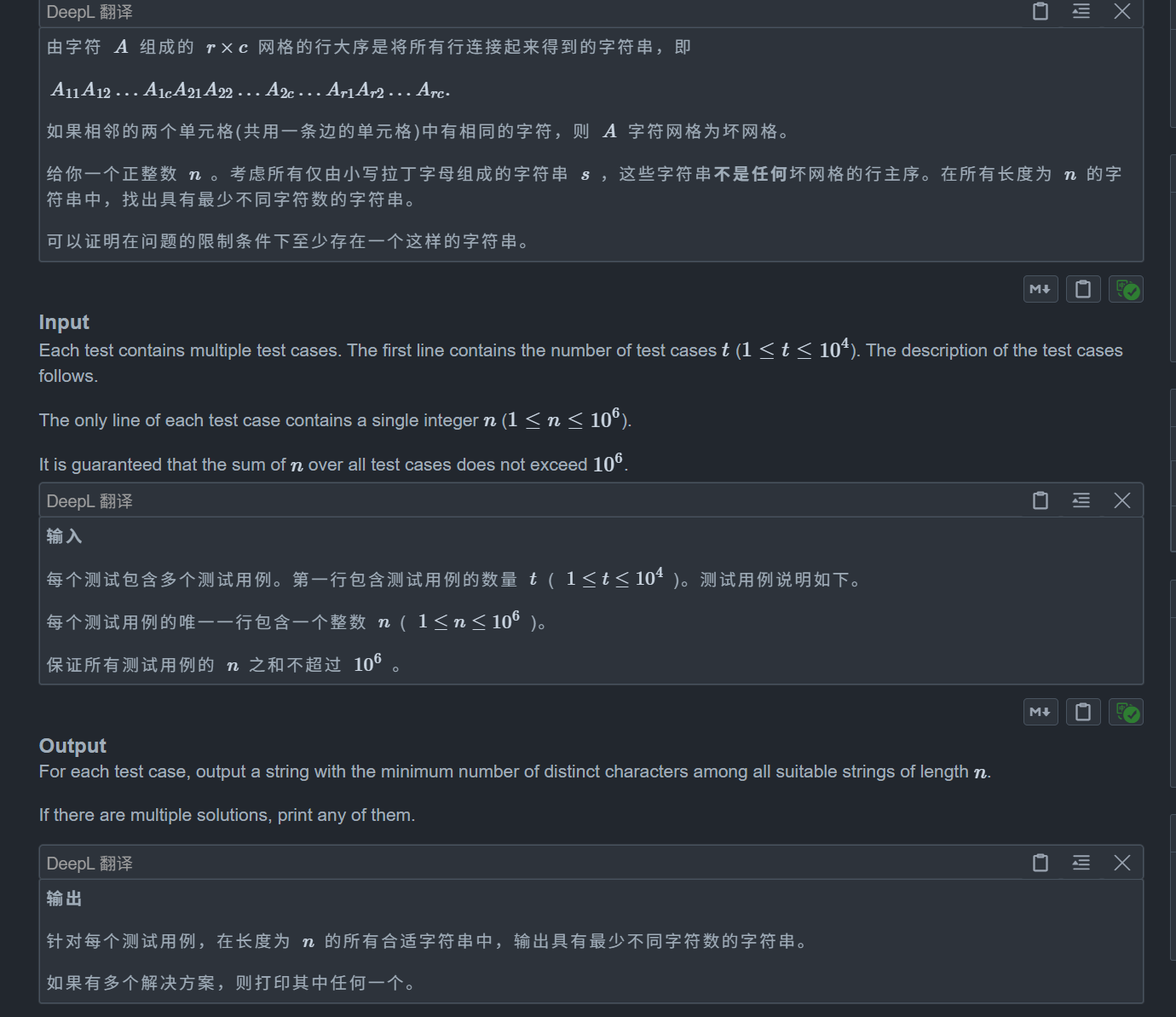
思路:
构造
观察能力强的或者会猜的能很快写出来
我们定义 d 为第一个不是 n 因数的数,那么说明之前 1 2 3 4 .... d-1 都是 n 的因数,题目中明确说明,对于 i,s[i] != s[i + x] 其中 x 是 n 的因数,那么只需要以 d 为周期填字母即可,证明
对于 1 ~ d-1 这些数,显然由于我们周期是 d,所以 s[i] = s[i + d] 才成立,所以之前的数都不可能成立
对于大于 d 的数,如果有 s[i] = s[j],那么显然有 j - i = k*d,而 d 不是 n 的因数,所以 k*d 不是 n 的因数,即不可能存在 x = k*d 使得 s[i] = s[i + x] 的情况,yw其不符合 x 是 n 的因数的条件
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"
int n;
void solve()
{cin >> n;int T = 1;while (!(n % T)){T++;}for (int i = 1; i <= n; i++){cout << (char)((i % T) + 'a');}cout << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}C. Strong Password
题目: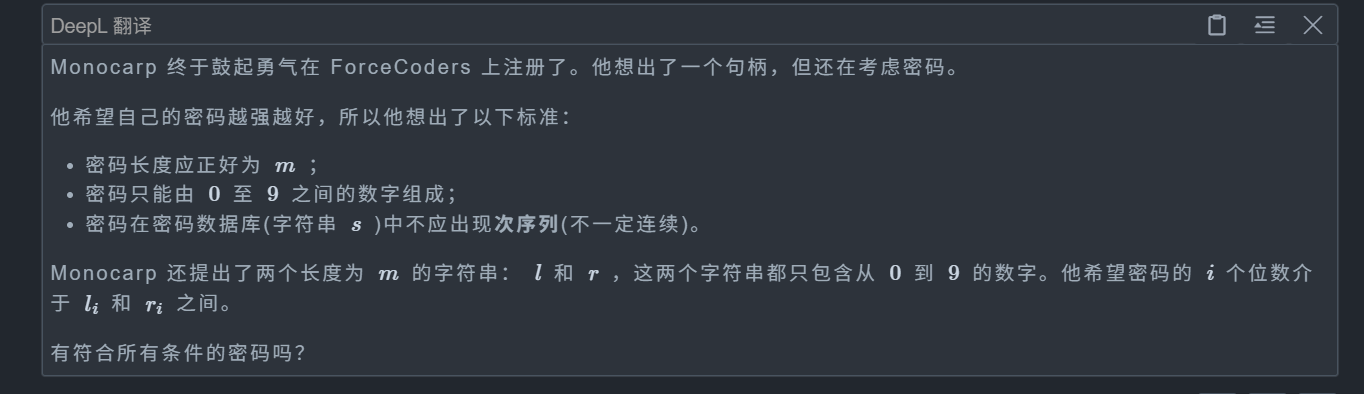
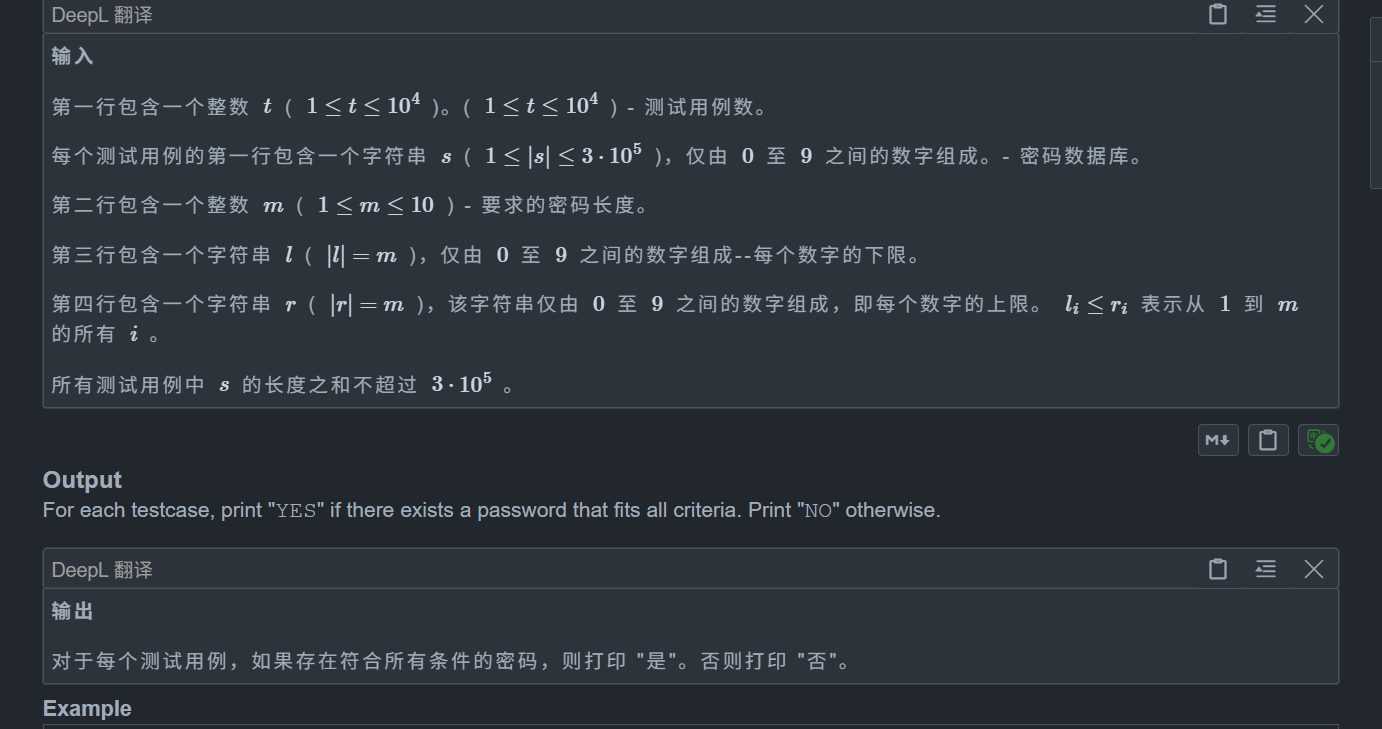 思路:
思路:
贪心
不考虑那么多,我们其实只需要找出一个不存在的情况即可,所以考虑极端情况
我们对每一位都二分找到最远的位置,如果有某一位找不到,那么就说明存在,否则就不可能
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = unsigned long long;
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int m;string s,l,r;cin >> s;cin >> m >> l >> r;int last = 0;set<int> p[10];for(int i = 0;i < s.size();i++){p[s[i] - '0'].insert(i+1);}for (int i = 0; i < m; i++){int temp = 0;for (int j = l[i] - '0'; j <= r[i] - '0'; j++){auto it = p[j].upper_bound(last);if(it == p[j].end()){yes;return;}temp = max(temp,*it);}last = max(last,temp);} no;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}