线段树学习笔记 - 摩尔投票问题

1. 前言

线段树系列文章：

• 线段树学习笔记
• 线段树学习笔记 - 练习题（1）
• 线段树学习笔记 - 练习题（2）
• 线段树学习笔记 - 练习题（3）
• 线段树学习笔记 - 动态开点线段树
• 线段树学习笔记 - 区间最值操作
• 线段树学习笔记 - 扫描线问题

这篇文章开始来学习下摩尔投票问题，学习视频：左程云算法讲解116【扩展】摩尔投票大加强，线段树里捉海王。首先看下什么是摩尔投票问题，直接看百度，摩尔投票法（Moore’s Voting Algorithm）是一种用于在数组中寻找多数元素的高效算法。多数元素是指在数组中出现次数超过一半的元素。摩尔投票法通过消除不同元素之间的对抗来找到可能的多数元素。

简而言之，摩尔投票就是给定一个数组，然后找到这个数组里面超过一半的数字，比如数组里面 [1，2，2，2，3]，最终的多数元素就是 2。那如果是 [1，2，2，3，3] 呢，这种就没有多数元素，因为 2 和 3 都没有超过数组长度的一半。

2. 解决思路

来看下如何找出这个数字，首先要在数组中做一个操作，就是将数组中两两不同的数字给删掉。比如 [a，b，c，d，d]，a 和 b 不同，删掉，数组剩下 [c，d，d]，然后 c 和 d 不同，删掉 c 和 d，剩下 [d]，最终剩下的这个 d 有可能是多数元素，也有可能不是多数元素。

然后我们再遍历数组，统计数组中 d 的个数 cnt，如果 cnt > length / 2，说明这个 d 就是多数元素，否则这个数组就没有多数元素。

为什么这么做可以获取到多数元素，是因为如果数组中有一个元素超过数组长度的一半，那么两两抵消之后最后肯定剩下这个数字。

上面就是思路，我们真实 code 肯定不会去遍历一个数字，然后用双重 for 循环再去找不同的数字给删掉，这样时间复杂度比较高。那么如果用 hash 表去统计所有数字出现的次数，这时候空间复杂度又会到 O(n)。实际上，用两个元素 cnt 和 currentMax 就可以求出来，遍历到一个数字，如果这个数字和 currentMax 不一样，那么 cnt - 1，如果一样，那么 cnt + 1，最终遍历完之后再遍历一遍数组统计 currentMax 的个数。

首先在下标 0，由于 cnt 初始值为 0，因此 curMax 直接设置为 1，cnt = 1，继续往下遍历。

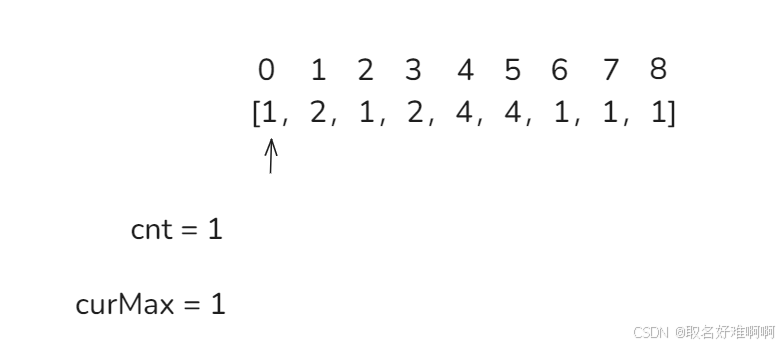
来到下标 1，发现此时下标值为 2，和 curMax 不相等，cnt - 1 = 0，继续往右遍历。

接下来来到下标 2，发现 cnt = 0，设置 cnt = 1，curMax = 2，继续遍历。

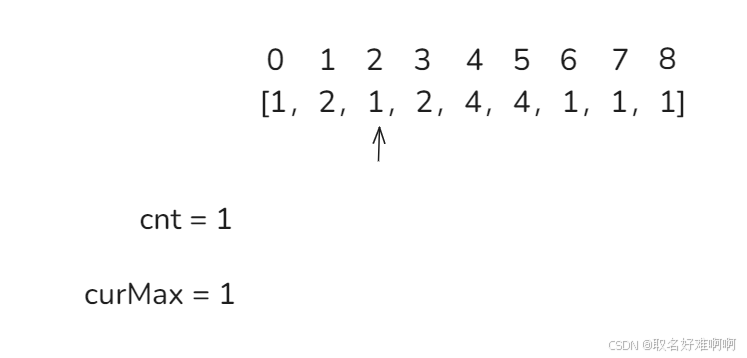
来到下标 3，发现 curMax != 2，将 cnt - 1，继续遍历。

下面来到下标 4，发现 cnt = 0，所以直接将 curMax 设置为 4，cnt 设置为 1，接着来到下标 5，发现和 curMax 相等，cnt + 1，继续遍历。

然后来到下标 6 和 下标 7，发现下标值和 curMax 不相等，都将 cnt - 1，此时 cnt = 0，注意遍历过程如果不相等 curMax 是不用管的，直接处理 cnt 就可以。

最后来到下标 8，发现此时 cnt = 0，那么将 curMax 设置为 1，遍历结束。

最后再次遍历数组，统计 curMax 出现的次数，发现出现了 5 次，大于 9 / 2，所以 5 就是我们要找的多数元素。

这里用了两个元素就完成了销毁这件事，如果发现数组下标值和 curMax 不相同，cnt - 1，意思就是两个不相同的元素抵消掉，当 cnt = 0，说明前面的元素都抵消了，本次将下标值先记录下来再往后遍历找不同数字来抵消。

上面就是能找到多数元素的，比如像下面这种遍历到之后剩下 4，这种就属于找不到多数元素的。

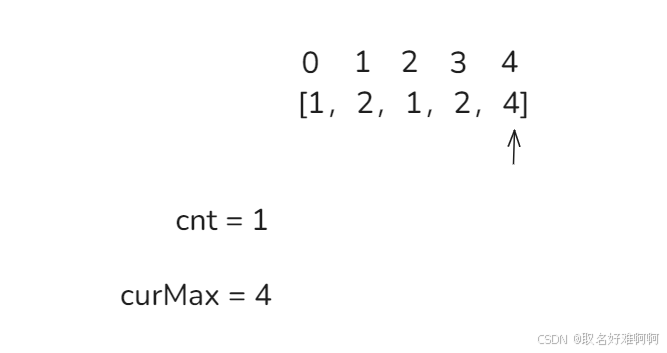
好了，下面来看下一道 leetCode 题目。

3. LeetCode 169 多数元素

LeetCode 169 多数元素。

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入： nums = [3,2,3]
输出： 3

示例 2：

输入： nums = [2,2,1,1,1,2,2]
输出： 2

提示：

• $n==nums.length$
• $1<=n<=5\ast 10^4$
• $-10^9<=nums[i]<=10^9$

这道题就是摩尔投票，代码按照上面的流程写就行，下面看下 code。

public int majorityElement(int[] nums) {int cnt = 0;int curMax = 0;for (int num : nums) {if (cnt == 0) {curMax = num;cnt = 1;} else if (num != curMax) {cnt--;} else {cnt++;}}// 比如 [1，2，1，2，1，2] 这种if (cnt == 0){return -1;}// 统计 curMax 个数cnt = 0;for(int num : nums){if(num == curMax){cnt++;}}return cnt > nums.length / 2 ? curMax : -1;
}

这里还是把前后的逻辑都写出来了，实际上由于题目确保了一定会有一个元素是符合要求的，因此后面统计 cnt 这段可以不用写，直接返回 curMax 就可以了，我这里是把剩下的判断逻辑都写出来了。

3. LeetCode 2780 合法分割的最小下标

LeetCode 2780 合法分割的最小下标。

如果在长度为 m 的整数数组 arr 中 超过一半 的元素值为 x，那么我们称 x 是 支配元素 。

给你一个下标从 0 开始长度为 n 的整数数组 nums ，数据保证它含有一个 支配 元素。

你需要在下标 i 处将 nums 分割成两个数组 nums[0, ..., i] 和 nums[i + 1, ..., n - 1] ，如果一个分割满足以下条件，我们称它是 合法 的：

• 0 <= i < n - 1
• nums[0, ..., i] 和 nums[i + 1, ..., n - 1] 的支配元素相同。
  这里， nums[i, ..., j] 表示 nums 的一个子数组，它开始于下标 j ，结束于下标 j ，两个端点都包含在子数组内。特别地，如果 j < i ，那么 nums[i, ..., j] 表示一个空数组。

请你返回一个 合法分割 的 最小 下标。如果合法分割不存在，返回 -1。

示例 1：

输入： nums = [1,2,2,2]
输出： 2
解释： 我们将数组在下标 2 处分割，得到 [1,2,2] 和 [2] 。
数组 [1,2,2] 中，元素 2 是支配元素，因为它在数组中出现了 2 次，且 2 * 2 > 3 。
数组 [2] 中，元素 2 是支配元素，因为它在数组中出现了 1 次，且 1 * 2 > 1 。
两个数组 [1,2,2] 和 [2] 都有与 nums 一样的支配元素，所以这是一个合法分割。
下标 2 是合法分割中的最小下标。

示例 2：

输入： nums = [2,1,3,1,1,1,7,1,2,1]
输出： 4
解释： 我们将数组在下标 4 处分割，得到 [2,1,3,1,1] 和 [1,7,1,2,1] 。
数组 [2,1,3,1,1] 中，元素 1 是支配元素，因为它在数组中出现了 3 次，且 3 * 2 > 5 。
数组 [1,7,1,2,1] 中，元素 1 是支配元素，因为它在数组中出现了 3 次，且 3 * 2 > 5 。
两个数组 [2,1,3,1,1] 和 [1,7,1,2,1] 都有与 nums 一样的支配元素，所以这是一个合法分割。

示例 3：

输入： nums = [3,3,3,3,7,2,2]
输出： -1
解释： 没有合法分割。

提示：

• $1<=nums.length<=10^5$
• $1<=nums[i]<=10^9$
• $nums有且只有一个支配元素。$

思路：

上面题目意思就是找一个分割点将原始数组分成两个数组，然后这两个数组的多数元素相同。那假设 x 是 arr1 和 arr2 的多数元素，就能证明 x 就是整个数组的多数元素，所以第一步，先找出整个数组的多数元素，如果找不到，直接返回。

如果能找到多数元素，从左到右遍历并且边遍历边统计这个元素的总数 cnt1，数组总数是 n，如果 cnt1 > (i + 1) / 2 并且 (cnt - cnt1) > (n - i - 1) / 2，说明这个分割点左右两边都符合，返回这个点，下面看下 code。

public int minimumIndex(List<Integer> nums) {int cnt = 0;int curMax = 0;for (int num : nums) {if (cnt == 0) {curMax = num;cnt = 1;} else if (num != curMax) {cnt--;} else {cnt++;}}if (cnt == 0) {return -1;}// 这个值总共出现了多少次cnt = 0;for (int num : nums) {if (num == curMax) {cnt++;}}if (cnt <= nums.size() / 2) {return -1;}int cnt1 = 0;// 开始找分割点for (int i = 0; i < nums.size(); i++) {if(nums.get(i) == curMax){cnt1++;}if(cnt1 > (i + 1) / 2 && (cnt - cnt1) > (nums.size() - i - 1) / 2){return i;}}return -1;
}

3. 查询出现次数 > n / k 的数

3.1 思路

给定一个数组，要求出这个数组中出现次数 > n / k 的数，k 是比较小的，比如 1 <= k <= 10 这种，要求返回这些数字。

来看下如何求出来，假设现在给定的数组是：[6，4，2，4，3，6，6，4]，k = 4，也就是说要找出数组中出现次数 > 2 的数字。

首先来看下最终返回的集合大小最多会是多少，由于集合里面的每一个数字出现次数都大于 n / k，假设集合里面的数字个数等于 k，那么 k * (n / k) > n 了，怎么可能比数组长度还长，所以最终最多有 (k - 1) 个数字满足条件。

接下来我们就创建一个大小为 k - 1 的集合，这个集合记录的原始是一个二维数组，比如是 cands，那么 cands[0] 表示候选数字，cands[1] 表示数字出现的个数。

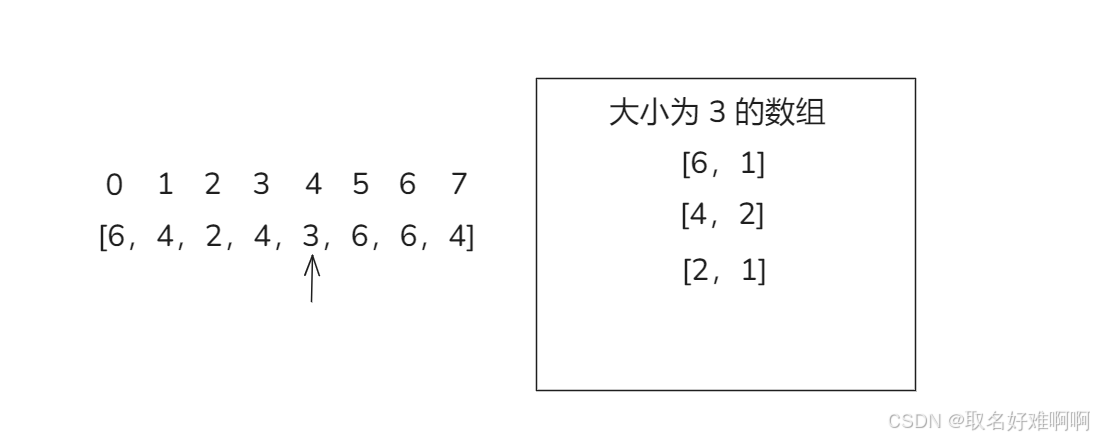
右边是遍历到下标 4 的时候数组里面的情况，下面遍历到 3，数组里面没有这个数字，这时候将数组里面每一个候选元素个数都 -1，然后为 0 的就从数组中删掉，然后这个 3 也不要了。

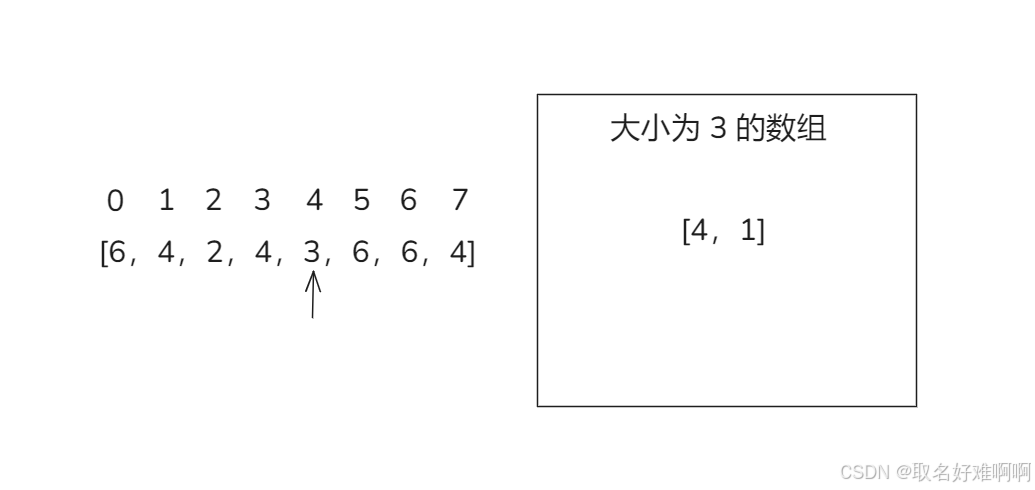
接下来遍历到 5、6、7，由于这个数组大小为 3，那么遍历到 下标 5 的时候 6 是可以直接加入数组的，遍历到 6、7 也是直接改个数就行。

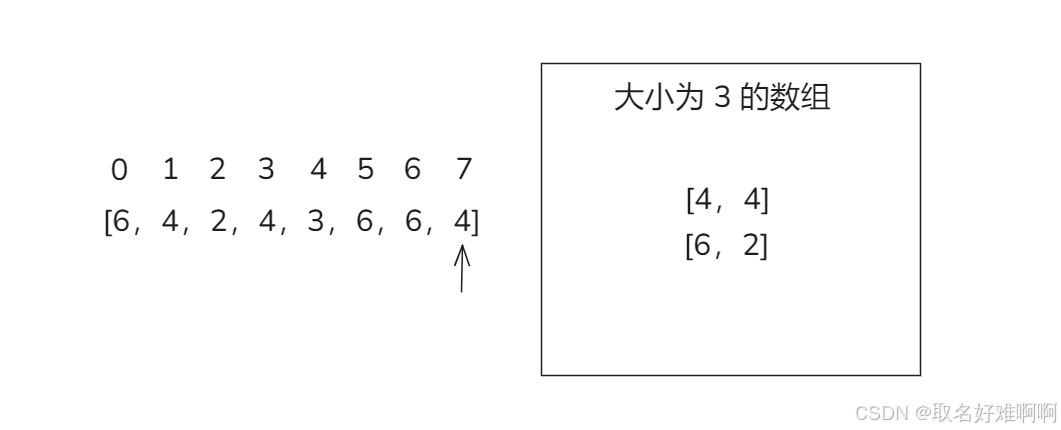
最终数组里面的 4 和 6 就是候选元素，然后再遍历一遍数组，统计 4 和 6 的出现次数，发现都是 3 次，因为 $3>8/4$，所以 4 和 6 都是符合题目要求的结果。

可以看到整体的逻辑就是遍历数组，然后把数字加入数组，分为三种情况：

1. 数组还没满，这时候数字直接加入。
2. 数组满了，但是数组里面有这个数字，那么出现次数 + 1。
3. 数组满了，而且数组里面没有这个数字，那么其他数字出现次数全部 - 1，如果减完之后为 0，就从数组删掉。

步骤比较简单，主要是来看下为什么这样做能够确保如果一个数字出现次数大于 k 次，就一定能在遍历完数组之后能保留在这个 k - 1 大的数组中，下面是个人理解。

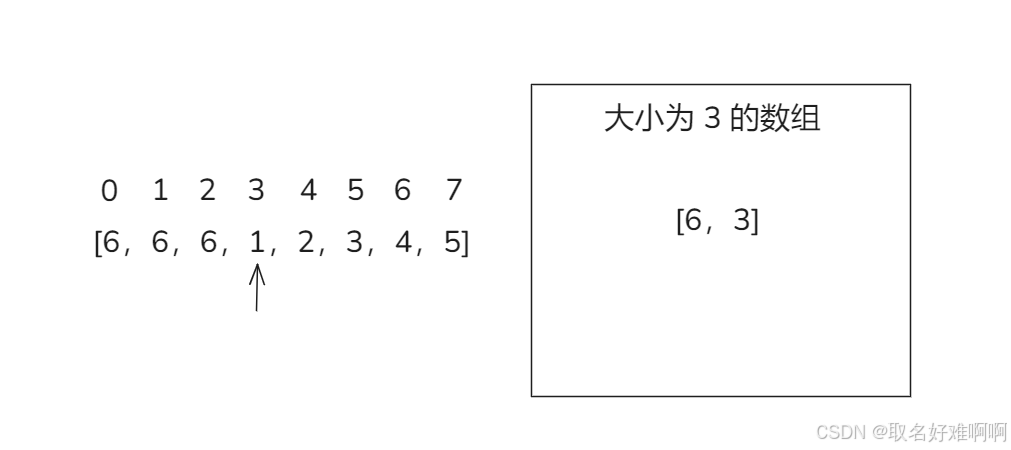
首先还是一样数组大小为 8，然后 k = 4，这时候遍历到下标 3，数组里面有 [6，3] 这个项。然后继续往右遍历，这时候遍历到 4、5，都会加入数组。

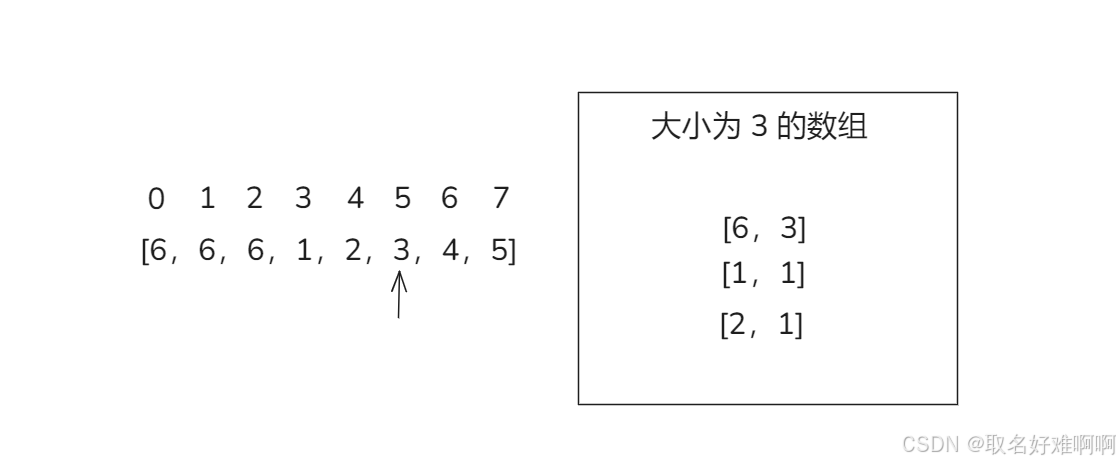
然后遍历到下标 5 的时候，发现数组满了，而且里面不存在 3，所以现在每一个数的 cnt 都需要 -1，为 0 的就删掉，变成下面这样，然后下标 5 的 3 也不要了，因为相当于这个 3 和数组里面的每一个数都抵消了一遍。

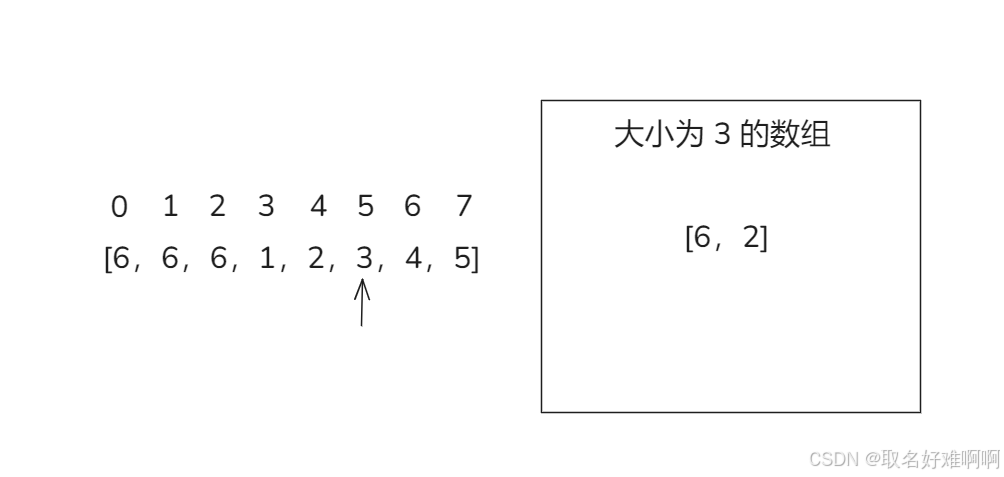
接下来加入 6、7 就可以直接往数组里面加入，不用删除了，所以当数组假设 x 就是候选值，x 的个数是大于 2 的，如果想要把 x 从数组中删掉，就上面的情况，那么最少需要 9 个不同的数字。

就比如上面现在数组里面有一个 k - 1 大小的数组，里面有一个 x，次数是 1，现在需要将 x 给删掉，是不是首先需要把这个数组填满，也就是需要 k - 2 个不同的数字，然后再需要一个不同的数字来将整个数组的次数都 -1，这样 x 才能变成 0，因此如果需要将 x 变成 0，就需要消耗 k - 1 个数字，所以上面要把 3 个 6 都消耗掉，最少需要 3 *（4 - 1）= 9 个数字。

那我们可以来看，因为候选值 x 是大于 n / k 的，就假设 x 出现的次数是最小值 n / k + 1，那么如果遍历完数组之后这个 x 不在数组里面，需要 (n / k + 1) * (k - 1) 个数字，也就是 $\frac{(k+n)\ast (k-1)}{k}+\frac{k+n}{k}=\frac{k^2+n\ast k}{k}=n+k$，这个数量是超过了数组长度的，所以说这个 x 肯定会留在数组里面。

那为什么说数组里面是候选值呢，其实看下面的图也能看出来， 数组是只要有空位就能往里面填，比如后面的 4、5 都填进去了，但是 4、5 不是最终结果。

3.2 题目 leetcode 229 多数元素 II

leetcode 229 多数元素 II。

给定一个大小为 n 的整数数组，找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。

示例 1：

输入： nums = [3,2,3]
输出： [3]

示例 2：

输入： nums = [1]
输出： [1]

示例 3：

输入： nums = [1,2]
输出： [1,2]

提示：

• $1<=nums.length<=5\ast 10^4$
• $10^9<=nums[i]<=10^9$

思路：

上面 3.1 是查询出现次数 > n / k 的，这里题目要求是超过 n / 3 的，所以把 3.1 的代码实现出来直接传入 k = 3 就行了。

class Solution {public static List<Integer> majorityElement(int[] nums) {return majority(nums, 3);}private static List<Integer> majority(int[] nums, int k) {List<Integer> res = new ArrayList<>();int[][] cands = new int[k - 1][2];k--;for (int num : nums) {update(num, cands);}for (int[] cand : cands) {if (cand[1] > 0) {int cnt = 0;for (int num : nums) {if (num == cand[0]) {cnt++;}}if (cnt > nums.length / (k + 1)) {res.add(cand[0]);}}}return res;}private static void update(int num, int[][] cands) {for (int i = 0; i < cands.length; i++) {if (num == cands[i][0]) {cands[i][1]++;return;}}for (int i = 0; i < cands.length; i++) {if (cands[i][1] == 0) {// 直接替换, 上面说如果为 0 就从数组删掉, 这里直接替换也相当于删除了cands[i][1] = 1;cands[i][0] = num;return;}}for (int i = 0; i < cands.length; i++) {if (cands[i][1] > 0) {cands[i][1] -= 1;}}}
}

因为这里 k = 3，创建出来的二维数组相当于 O(1) 了。而且类似这种 n / k 的题目，给出的 k 都是很小的，所以直接遍历就可以。

4. 分治查询多数元素

假设现在又一个很长的数组 10^9 的级别，现在需要查询出多数元素是什么，为了加快速度查询速度可以使用多线程并发查询，一个线程负责一段，查询出来进行汇总，下面来看下如何汇总。

首先查询还是按照第二小节的思路，查询的结果是一个数组 cands，cands[0] = 候选数字，cands[1] = 个数，下面假设左右两边都查出来了这个数组。

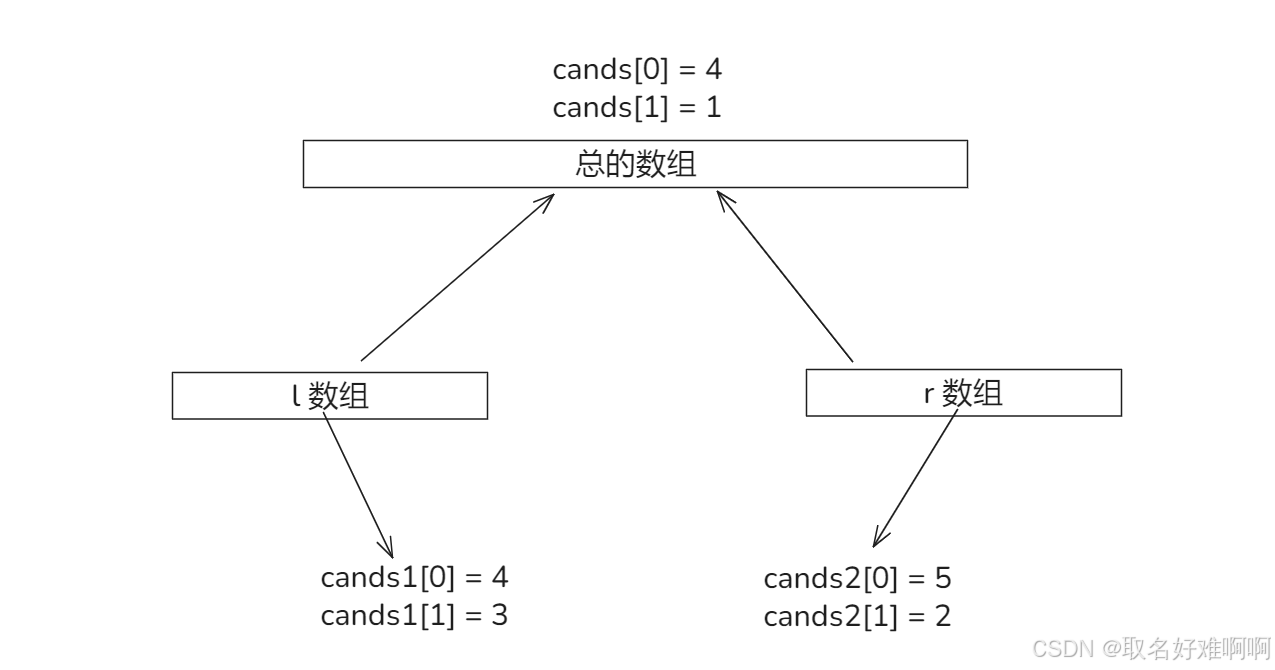
左边候选数是 4，数量是 3，右边侯选数是 5，数量是 2，这时候汇总需要将左边的候选者和右边的候选者再进行一轮 pk，就是不同数字相互抵消，最终就剩下一个 4，因此汇总之后我们能够得到最终的摩尔数就是 4。

那如果左边候选和右边候选数都相同，这种情况下汇总之后的数量就是相加的，也就是 cands[1] = cands1[1] + cands2[1]。这里就是根据小范围的海王数汇总出整体范围的海王数。

那么这里演示汇总就是为了下面的线段树，也就是线段树维护任意区间的海王数。

5. 线段树维护区间海王数

5.1 结构和方法

上面第 4 小节我们把区间维护的逻辑都说了，现在可以看下具体需要需要哪些结构。

首先就是候选者数组和数量数组，因为需要根据左右节点来维护出父结点的海王数，就得需要知道左右节点的海王数和个数是多少。

// 海王数
public static int[] cands = new int[MAXN << 2];// 经过碰撞之后剩余的个数是多少
public static int[] cnt = new int[MAXN << 2];

然后来看下 up 方法，就是根据左右的海王数汇总出父结点的海王数。

private void up(int i) {// 左边的海王数int lc = cands[i << 1];// 右边的海王数int rc = cands[i << 1 | 1];// 左边的海王数剩余的个数int lcount = cnt[i << 1];// 右边的海王数剩余的个数int rcount = cnt[i << 1 | 1];// 如果左边的海王数等于右边的, 那么最终的海王数就是 lc// 如果不等于, 那么就看如果左边的海王数的剩余个数多, 那么经过碰撞最终的海王数就是 lc// 如果不相等，同时右边的海王数剩余个数比左边的多，那么经过碰撞最终的海王数就是 rccands[i] = lc == rc || lcount >= rcount ? lc : rc;// 如果两边海王数相等就相加, 否则就是绝对值cnt[i] = lc == rc ? lcount + rcount : Math.abs(lcount - rcount);
}

5.2 题目 leetcode1157 子数组中占绝大多数的元素

然后下面看一道题目：leetcode1157 子数组中占绝大多数的元素。

设计一个数据结构，有效地找到给定子数组的 多数元素 。

子数组的 多数元素 是在子数组中出现 threshold 次数或次数以上的元素。

实现 MajorityChecker 类:

• MajorityChecker(int[] arr) 会用给定的数组 arr 对 MajorityChecker 初始化。
• int query(int left, int right, int threshold) 返回子数组中的元素 arr[left...right] 至少出现 threshold 次数，如果不存在这样的元素则返回 -1。

示例 1：

输入:
[“MajorityChecker”, “query”, “query”, “query”]
[[[1, 1, 2, 2, 1, 1]], [0, 5, 4], [0, 3, 3], [2, 3, 2]]
输出：
[null, 1, -1, 2]

解释：
MajorityChecker majorityChecker = new MajorityChecker([1,1,2,2,1,1]);
majorityChecker.query(0,5,4); // 返回 1
majorityChecker.query(0,3,3); // 返回 -1
majorityChecker.query(2,3,2); // 返回 2

提示：

• 1 <= arr.length <= 2 * $10^4$
• 1 <= arr[i] <= 2 * $10^4$
• 0 <= left <= right < arr.length
• threshold <= right - left + 1
• 2 * threshold > right - left + 1
• 调用 query 的次数最多为 $10^4$

思路：

这里我们既然需要找到 [l，r] 范围的多数元素，首先假设我们能通过线段树维护这个区间的海王数，也就是通过线段树最终能知道这个范围内的多数元素是谁，然后拿到这个元素，需要再去原数组搜索这个数字在 [l，r] 这个区间的出现次数，搜索可以用二分。

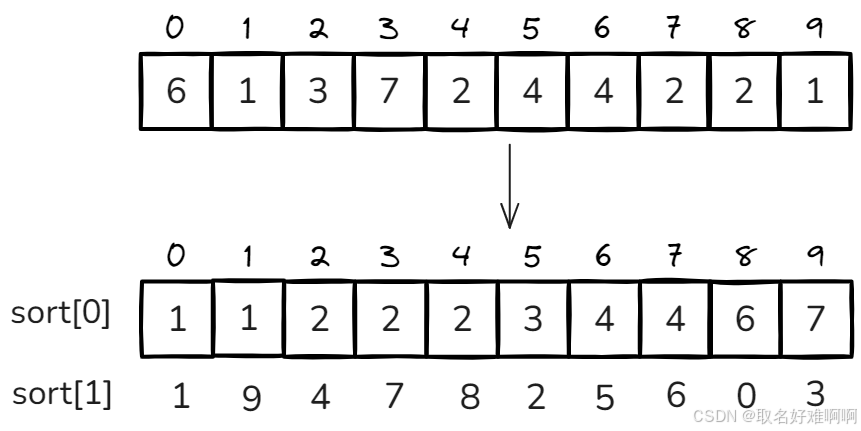
上面是原数组，下面是排序之后的，我们用一个二维数组 sort 存储原数组的值和下标，然后先按数字大小排序，如果数字相同再按照下标从小到大排序。现在假设我要求 4 - 6 范围上面的多数数字，经过线段树维护之后得到结果是 4，然后现在要到 sort 数组中二分。

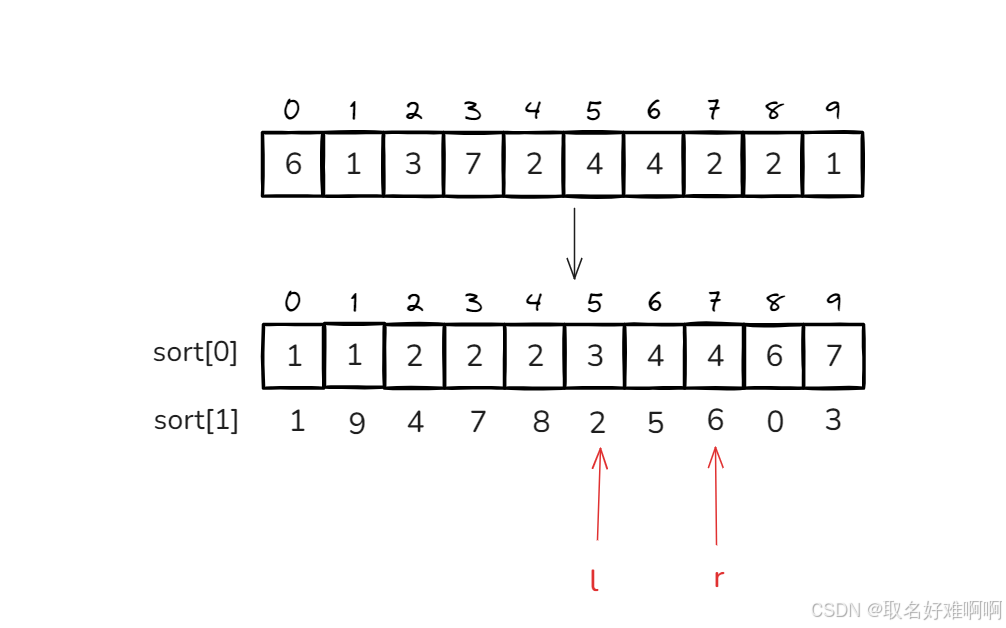
首先我们找到 [0，6] 范围上 4 的个数，先二分找到 4 的位置，找到了 4 的位置之后再根据下标二分找到下标 6 的位置。

然后我们找 [0，3] 范围上 4 的个数，也是一样先二分找到 4 的位置，然后再根据下标去二分。最终 6 - 4 就是我们要的结果。

所以流程就是先二分找到这个侯选数的大致范围，然后再通过下标二分找到这个候选数的具体下标，用 [0，r] - [0，l - 1] 就得到侯选数的数字了。

最终看下整体的 code。

class MajorityChecker {public int n = 0;public static int MAXN = 20001;public static int[][] sort = new int[MAXN][2];public static int[] cands = new int[MAXN << 2];public static int[] cnt = new int[MAXN << 2];public MajorityChecker(int[] arr) {n = arr.length;buildArr(arr);buildTree(arr, 1, n, 1);}private void buildTree(int[] arr, int l, int r, int i) {if (l == r) {cands[i] = arr[l - 1];cnt[i] = 1;} else {int mid = l + ((r - l) >> 1);buildTree(arr, l, mid, i << 1);buildTree(arr, mid + 1, r, i << 1 | 1);up(i);}}private void up(int i) {int lc = cands[i << 1];int rc = cands[i << 1 | 1];int lcount = cnt[i << 1];int rcount = cnt[i << 1 | 1];// 相同就是 lc, 不同就看哪个数量大cands[i] = lc == rc || lcount >= rcount ? lc : rc;// 相同就累加, 不相同就取 abscnt[i] = lc == rc ? lcount + rcount : Math.abs(lcount - rcount);}private void buildArr(int[] arr) {// 记录 sort 数组，用于二分查找侯选数个数for (int i = 0; i < arr.length; i++) {sort[i][0] = arr[i];sort[i][1] = i;}Arrays.sort(sort, 0, arr.length, (o1, o2) -> {if (o1[0] != o2[0]) {// 数字从小到大排序return o1[0] - o2[0];} else {// 数字相同根据下标排序return o1[1] - o2[1];}});}public int query(int left, int right, int threshold) {// 下标从 1 开始int[] res = queryCands(left + 1, right + 1, 1, n, 1);// 侯选数int cand = res[0];// 查询候选数个数是否大于 thresholdreturn find(cand, left, right) >= threshold ? cand : -1;}private int find(int cand, int left, int right) {// [0, right] 的return search(cand, right) - search(cand, left - 1);}private int search(int target, int i) {int l = 0, r = n - 1;while (l <= r) {// 按数字二分int mid = l + ((r - l) >> 1);if (sort[mid][0] > target) {r = mid - 1;} else if (sort[mid][0] < target) {l = mid + 1;} else {// 按照下标二分if (sort[mid][1] > i) {r = mid - 1;} else if (sort[mid][1] < i) {l = mid + 1;} else {return mid + 1;}}}return l;}// 查询private int[] queryCands(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {// 范围内直接返回return new int[]{cands[i], cnt[i]};}int mid = l + ((r - l) >> 1);if (jobr <= mid) {return queryCands(jobl, jobr, l, mid, i << 1);}if (jobl > mid) {return queryCands(jobl, jobr, mid + 1, r, i << 1 | 1);}// 先查出左边的候选数int[] lc = queryCands(jobl, jobr, l, mid, i << 1);// 先查出右边的候选数int[] rc = queryCands(jobl, jobr, mid + 1, r, i << 1 | 1);int lCands = lc[0], lCnt = lc[1];int rCands = rc[0], rCnt = rc[1];if (lCands == rCands) {// 如果左右候选相同，汇总return new int[]{lCands, lCnt + rCnt};} else {// 不相同就看碰撞之后谁剩下的个数多int fCands = lCnt >= rCnt ? lCands : rCands;int fCnt = Math.abs(lCnt - rCnt);return new int[]{fCands, fCnt};}}
}

如有错误，欢迎指出！！！！