《深入理解priority_queue:的使用与模拟实现》
《深入理解priority_queue:的使用与模拟实现》
文章目录
- 《深入理解priority_queue:的使用与模拟实现》
- 一、priority_queue的介绍
- 二、仿函数
- 2.1 仿函数的概念
- 2.2 仿函数的应用
- 2.3 仿函数与函数指针的对比
- 三、priority_queue的使用
- 3.1 冒泡排序
- 3.2 建立大堆和小堆
- 3.3 自定义类型的比较(日期比较)
- 3.3 数组中第k个大的元素
- 3.3.1 题目
- 3.3.2 解题思路
- 3.3.3 源代码
- 四、priority_queue的模拟实现
- 4.0 重载()实现
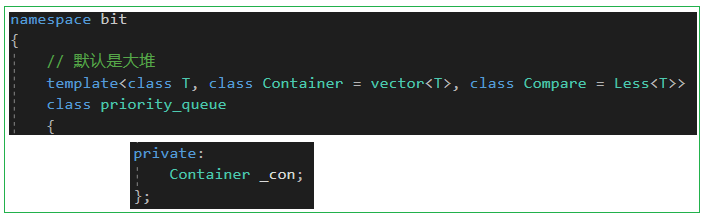
- 4.1 定义成员变量
- 4.2 push插入接口实现
- 4.3 pop删除接口实现
- 4.4 size、empty、top接口实现
- 4.4 模拟实现源代码
一、priority_queue的介绍
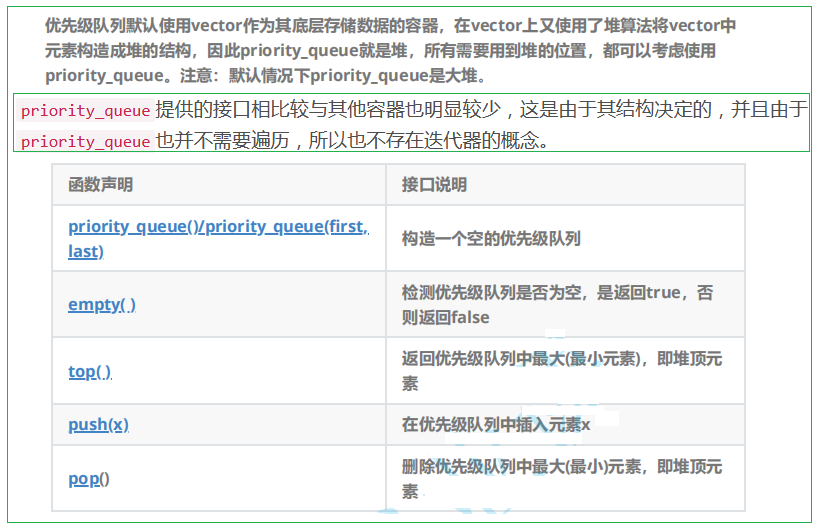
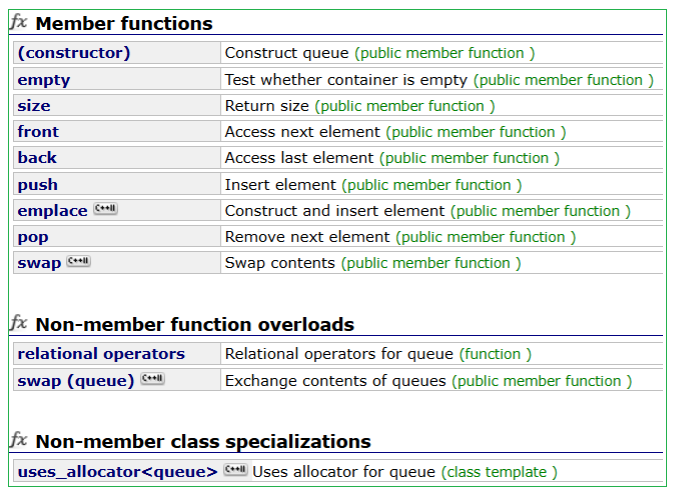
priority_queue即为优先级队列,它是STL对数据结构中堆的具体封装,因为priority_queue的头文件倍包含在queue的头文件中,,并且使用优先级队列建堆,默认为大堆。 所以使用时只需要包含头文件#include < queue>

priority_queue的模版参数有三个,第一个T是我们的元素类型,第二个Container是我们的容器适配器,第三个Compare是我们的仿函数 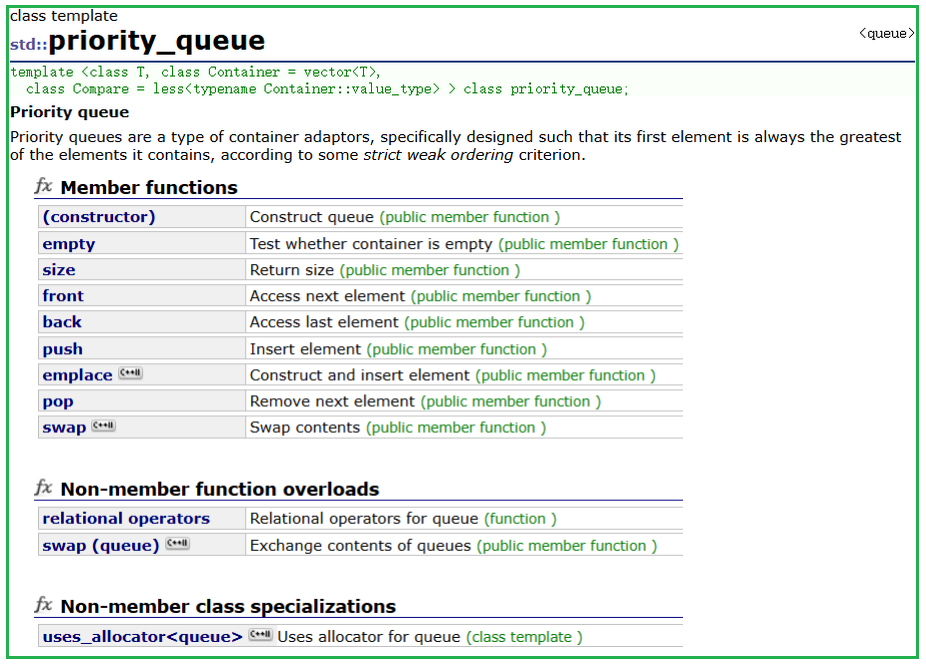

二、仿函数
2.1 仿函数的概念
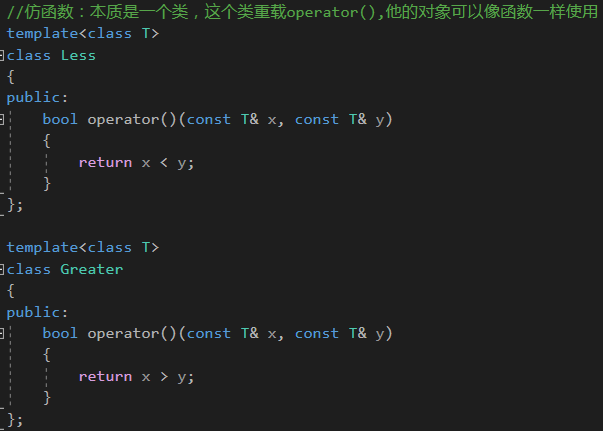
priority_queue的第三个末班参数 Campare----仿函数
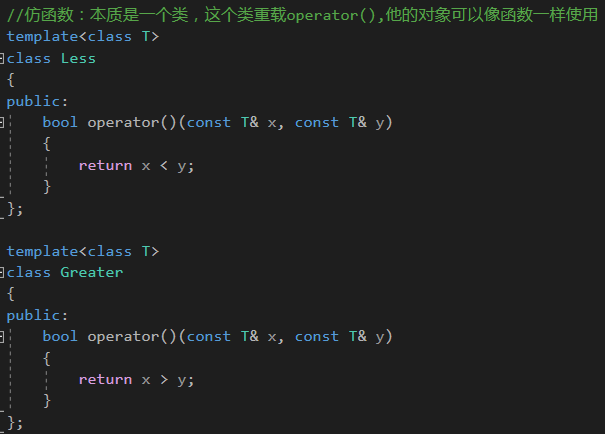
仿函数(Functor)是一种行为类似函数的对象,它可以被用作函数并接受参数。在 C++ 中,仿函数通常是重载了函数调用运算符 operator()的类对象。通过重载 operator(),仿函数可以像函数一样被调用,并且可以保存状态信息
我们可以通过定义对象的方式调用吗,也可以通过完整的类调用函数的方式调用
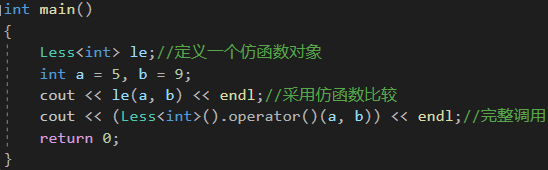
2.2 仿函数的应用
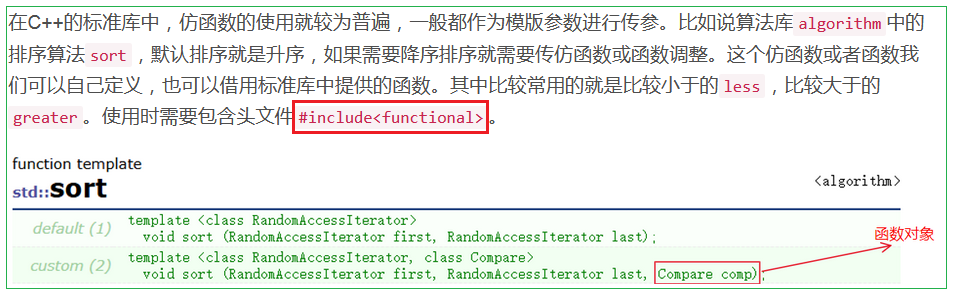
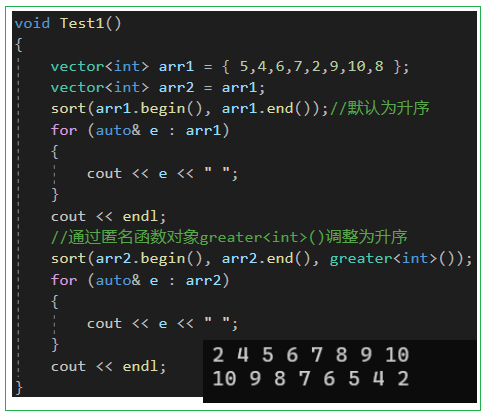
2.3 仿函数与函数指针的对比
仿函数的用法与C语言中的函数指针很相似,或说就是为了简化C语言的函数指针,C++引入仿函数

三、priority_queue的使用
这里就相当于数据结构中的堆! 二叉树的堆
3.1 冒泡排序
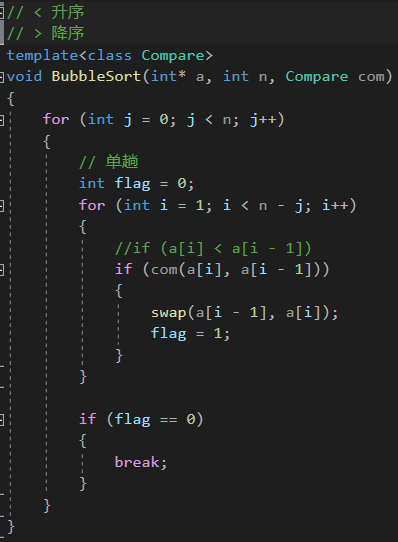
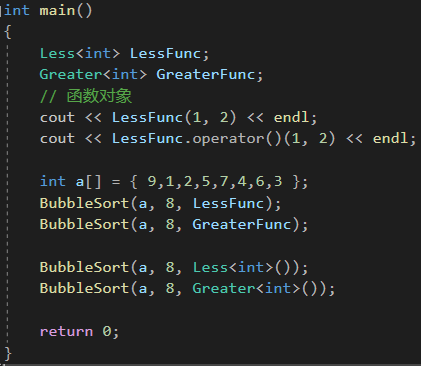
代码如下(示例):
// < 升序
// > 降序
template<class Compare>
void BubbleSort(int* a, int n, Compare com)
{for (int j = 0; j < n; j++){// 单趟int flag = 0;for (int i = 1; i < n - j; i++){//if (a[i] < a[i - 1])if (com(a[i], a[i - 1])){swap(a[i - 1], a[i]);flag = 1;}}if (flag == 0){break;}}
}int main()
{Less<int> LessFunc;Greater<int> GreaterFunc;// 函数对象cout << LessFunc(1, 2) << endl;cout << LessFunc.operator()(1, 2) << endl;int a[] = { 9,1,2,5,7,4,6,3 };BubbleSort(a, 8, LessFunc);BubbleSort(a, 8, GreaterFunc);BubbleSort(a, 8, Less<int>());BubbleSort(a, 8, Greater<int>());return 0;
}
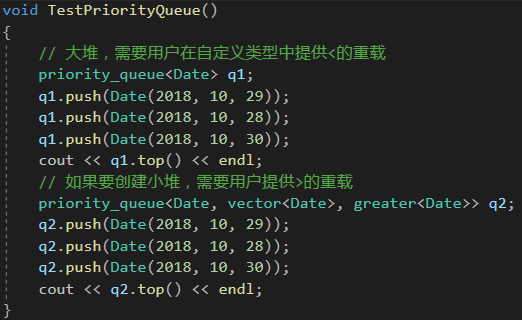
3.2 建立大堆和小堆
1.默认情况下,priority_queue是大堆
2.如果要创建小堆,将第三个模版参数换成greater比较方式
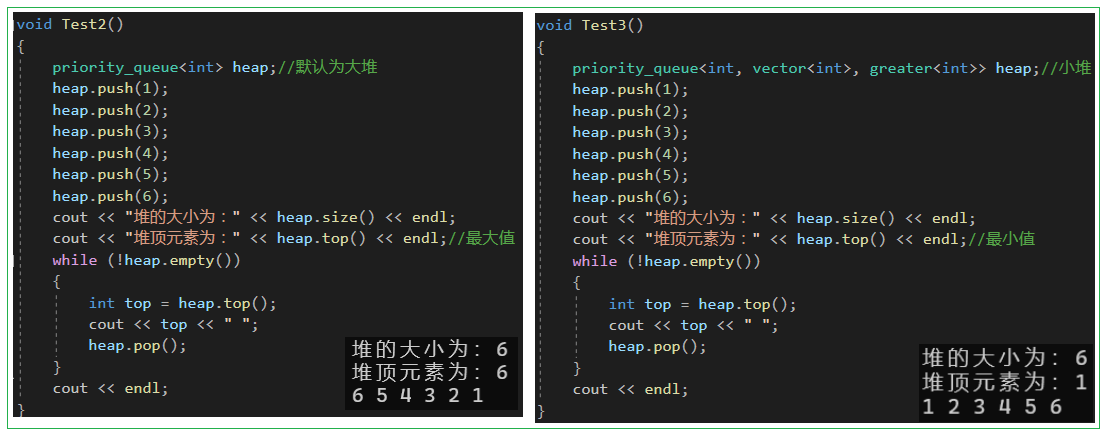
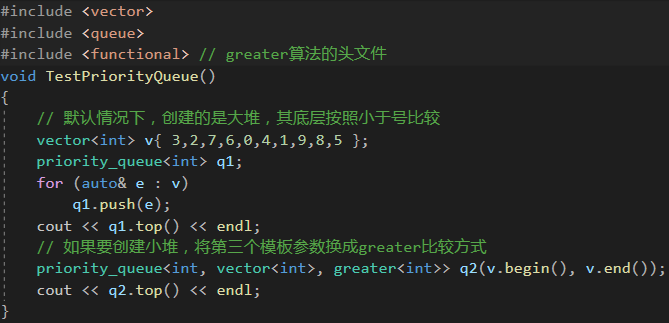
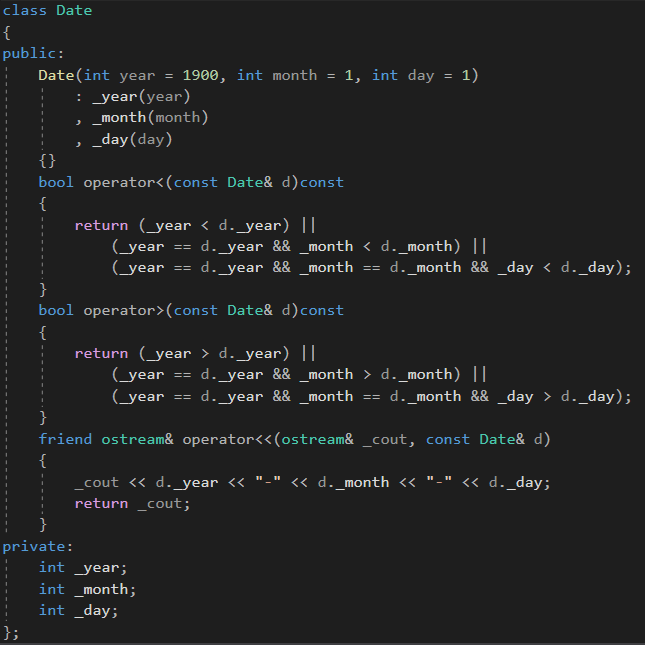
3.3 自定义类型的比较(日期比较)
如果在priority_queue中放自定义类型的数据,用户需在自定义类型中提供> 或者< 的重载。

3.3 数组中第k个大的元素
数组中第k个大的元素
3.3.1 题目

3.3.2 解题思路

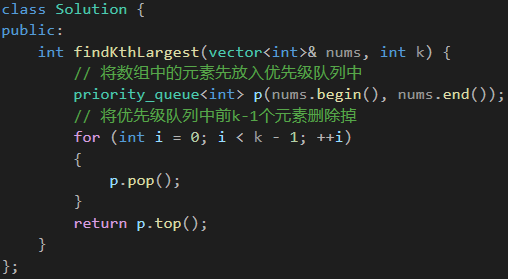
3.3.3 源代码
代码如下(示例):
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {// 将数组中的元素先放入优先级队列中priority_queue<int> p(nums.begin(), nums.end());// 将优先级队列中前k-1个元素删除掉for (int i = 0; i < k - 1; ++i){p.pop();}return p.top();}
};
四、priority_queue的模拟实现
通过对priority_queue的底层结构就是堆,因此只需对其进行通用的封装即可!
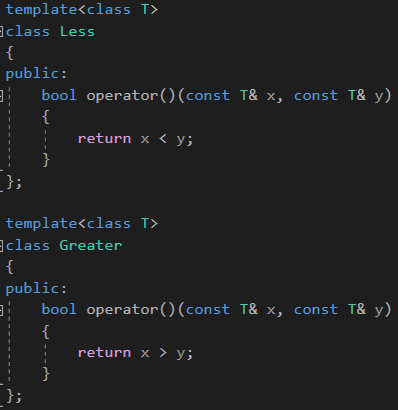
4.0 重载()实现
4.1 定义成员变量
4.2 push插入接口实现
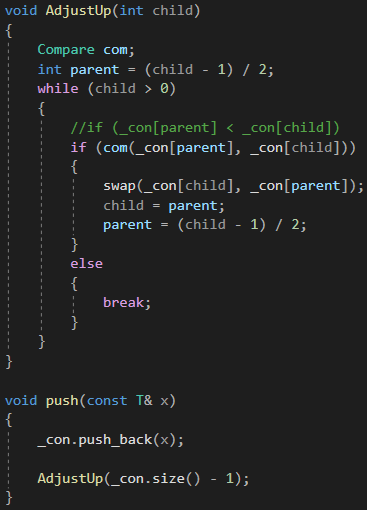
向堆的末尾插入新的元素,然后与父节点比较,然后判断是有需要向上调整!
向上调整函数:二叉树堆
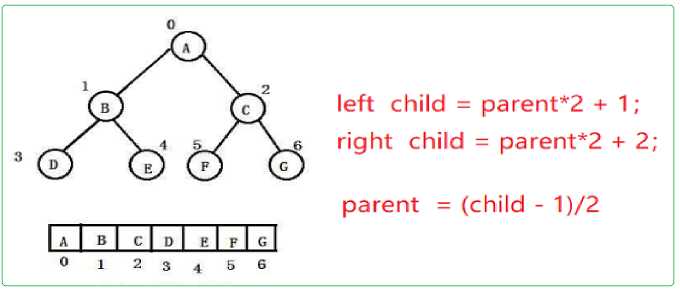
代码如下(示例):
void AdjustUp(int child){Compare com;int parent = (child - 1) / 2;while (child > 0){//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1);}
4.3 pop删除接口实现
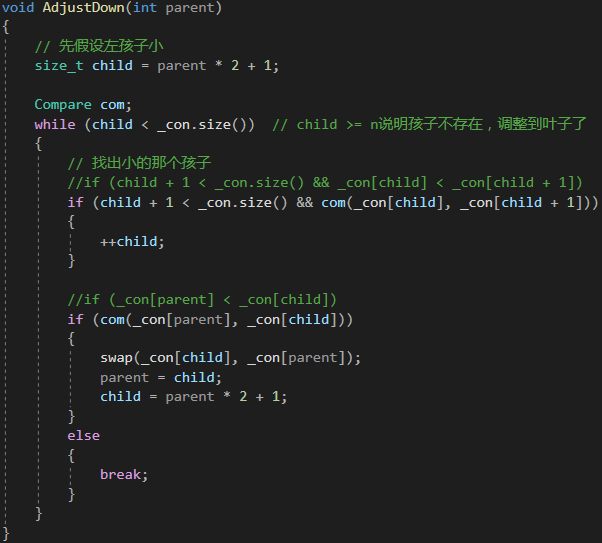
先将堆顶元素与最后一个元素交换,将删除堆顶元素转化为删除末尾元素,然后再对堆顶元素进行向下调整!
向上调整函数:二叉树堆
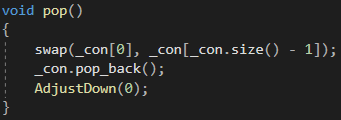
代码如下(示例):
void AdjustDown(int parent){// 先假设左孩子小size_t child = parent * 2 + 1;Compare com;while (child < _con.size()) // child >= n说明孩子不存在,调整到叶子了{// 找出小的那个孩子//if (child + 1 < _con.size() && _con[child] < _con[child + 1])if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){++child;}//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}
4.4 size、empty、top接口实现
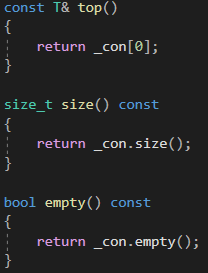
4.4 模拟实现源代码
代码如下(示例):
#pragma once#include<vector>template<class T>
class Less
{
public:bool operator()(const T& x, const T& y){return x < y;}
};template<class T>
class Greater
{
public:bool operator()(const T& x, const T& y){return x > y;}
};namespace bit
{// 默认是大堆template<class T, class Container = vector<T>, class Compare = Less<T>>class priority_queue{public:void AdjustUp(int child){Compare com;int parent = (child - 1) / 2;while (child > 0){//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1);}void AdjustDown(int parent){// 先假设左孩子小size_t child = parent * 2 + 1;Compare com;while (child < _con.size()) // child >= n说明孩子不存在,调整到叶子了{// 找出小的那个孩子//if (child + 1 < _con.size() && _con[child] < _con[child + 1])if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){++child;}//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}const T& top(){return _con[0];}size_t size() const{return _con.size();}bool empty() const{return _con.empty();}private:Container _con;};
}