#Datawhale 组队学习#强化学习Task5

强化学习Task1：#Datawhale组队学习#7月-强化学习Task1-CSDN博客

强化学习Task2：#Datawhale组队学习#7月-强化学习Task2-CSDN博客

强化学习Task4：#Datawhale 组队学习#强化学习Task4-CSDN博客

本篇是Task5，第九章策略梯度，第十章Actor-Critic算法。

第九章策略梯度

9.1 基于价值算法的缺点

以DQN为代表的基于价值算法的缺点：

无法表示连续动作

高方差

探索与利用的平衡问题

💡 工程师洞见：当遇到连续控制、高维动作或需要随机策略的场景（如金融交易），直接转向策略梯度方法

9.2 策略梯度算法

策略梯度算法是一类直接对策略进行优化的算法。

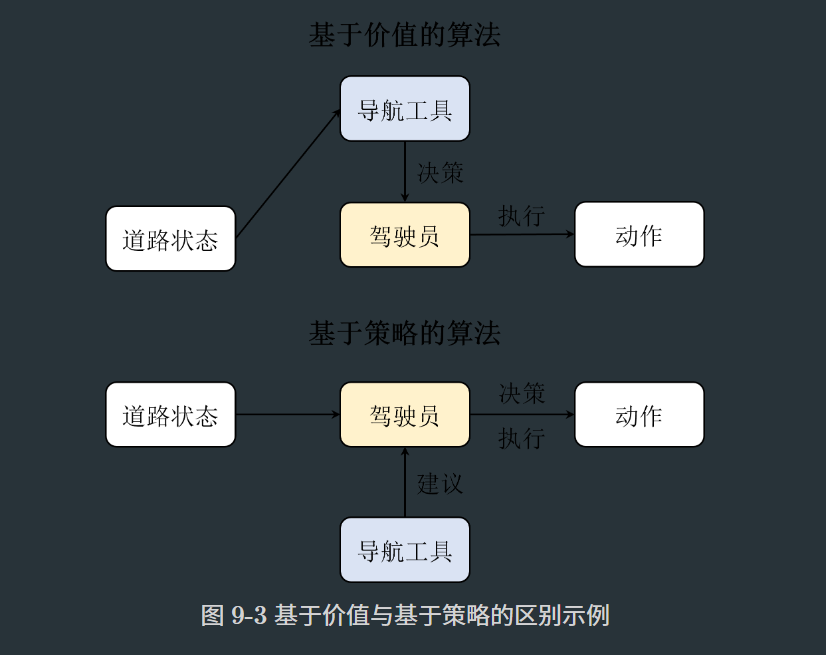
 我们再总结基于价值和基于策略算法的区别，以便于加深理解。我们知道，基于价值的算法是通过学习价值函数来指导策略的，而基于策略的算法则是对策略进行优化，并且通过计算轨迹的价值期望来指导策略的更新。举例来说，如下图所示，基于价值的算法相当于是在学一个地图导航工具，它会告诉并指导驾驶员从当前位置到目的地的最佳路径。但是这样会出现一个问题，就是当地图导航工具在学习过程中产生偏差时会容易一步错步步错，也就是估计价值的方差会很高，从而影响算法的收敛性。

 而基于策略的算法则是直接训练驾驶员自身，并且同时也在学地图导航，只是这个时候地图导航只会告诉驾驶员当前驾驶的方向是不是对的，而不会直接让驾驶员去做什么。换句话说，这个过程，驾驶员和地图导航工具的训练是相互独立的，地图导航工具并不会干涉驾驶员的决策，只是会给出建议。这样的好处就是驾驶员可以结合经验自己去探索，当导航工具出现偏差的时候也可以及时纠正，反过来当驾驶员决策错误的时候，导航工具也可以及时矫正错误。

工程意义：

1. 直接优化策略：参数θ更新方向使高回报动作概率↑，低回报动作概率↓

2. 无需动作价值最大化：规避了维数灾难问题

3. 天然支持随机策略：通过π(a|s)的概率分布实现探索

9.3 REINFORCE算法

我们可以不必采样所有的轨迹，而是采样一部分且数量足够多的轨迹，然后利用这些轨迹的平均值来近似求解目标函数的梯度。这种方法就是蒙特卡洛策略梯度算法，也称作REINFORCE算法。

工程陷阱与解决方案：

问题	现象	解决方案
高方差	训练曲线剧烈震荡	引入基线值 (baseline)
采样效率低	收敛速度慢	使用并行环境采样
奖励尺度敏感	梯度爆炸/消失	奖励归一化 (Reward Scaling)
探索不足	早期陷入局部最优	增加熵正则项

9.4 策略梯度推导进阶

在展开进阶版策略梯度推导之前，我们需要先铺垫一些概念，首先是马尔可夫链的平稳分布。平稳分布，顾名思义就是指在无外界干扰的情况下，系统长期运行之后其状态分布会趋于一个固定的分布，不再随时间变化。已经跑过一些强化学习实战的读者们也会发现，每次成功跑一个算法，奖励曲线都会收敛到一个相对稳定的值，只要环境本身不变，哪怕换一种算法，奖励曲线也会收敛到一个相对稳定的值，除非我们改动了环境的一些参数比如调奖励等，这就是平稳分布的概念。

 平稳分布本质上也是熵增原理的一种体现。

9.5 策略函数的设计

对于策略函数来说，我们也可以采用类似的设计，只不过我们输出的不是Q值，而是各个动作的概率分布。其实动作概率分布在实现上跟Q值的唯一区别就是必须都大于0且和为1，最简单的做法是在Q网络模型的最后一层增加处理层，一般称作为动作层 （action layer）。由于原来 Q 网络模型输出的值是有正有负的，怎么把它们转换成动作概率分布呢？我们通常采取目前比较流行的方式，即用 Softmax 函数来处理。

9.6 习题

1. 基于价值和基于策略的算法各有什么优缺点？

基于价值的算法（如Q-learning）通过优化价值函数间接学习策略，优点是样本效率高、收敛稳定，适合离散动作空间；缺点是难以处理连续动作和高维问题，且无法学习随机策略。基于策略的算法（如策略梯度）直接优化策略函数，优点是支持连续动作空间和随机策略，探索能力更强；缺点是训练方差大、收敛慢，且样本效率较低。

2. 马尔可夫平稳分布需要满足什么条件？

马尔可夫平稳分布需要满足两个核心条件：一是状态转移概率必须时齐（不随时间变化），即状态转移矩阵恒定；二是存在一个概率分布 d(s)，使得对所有状态 s，满足 d(s)=∑s′P(s′∣s)d(s′)，即长期状态下状态分布保持稳定。

3. REINFORCE 算法会比 Q-learning 算法训练速度更快吗？为什么？

REINFORCE算法通常比Q-learning训练速度慢。REINFORCE是蒙特卡洛策略梯度方法，需采样完整轨迹后才能更新，样本效率低且梯度方差大；Q-learning使用时序差分（TD）更新，支持单步学习，能更快利用经验，尤其在奖励稀疏环境下训练更高效。

4. 确定性策略与随机性策略的区别？

确定性策略在给定状态下输出唯一确定的动作，适合完全可观测环境，但探索能力弱；随机性策略输出动作的概率分布，通过概率采样实现探索，适合部分可观测或需随机决策的场景（如博弈），但可能增加训练复杂度。

---

第十章Actor-Critic算法

10.1 策略梯度算法的缺点

这里策略梯度算法特指蒙特卡洛策略梯度算法，即REINFORCE算法。 相比于DQN之类的基于价值的算法，策略梯度算法有以下优点。

• 适配连续动作空间。在将策略函数设计的时候我们已经展开过，这里不再赘述。
• 适配随机策略。由于策略梯度算法是基于策略函数的，因此可以适配随机策略，而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的，而基于价值的算法则是有偏的。

 但同样的，策略梯度算法也有其缺点。

• 采样效率低。由于使用的是蒙特卡洛估计，与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的，这个问题在前面相关章节中也提到过。
• 高方差。虽然跟基于价值的算法一样都会导致高方差，但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差，这样的方差甚至比基于价值的算法还要高。
• 收敛性差。容易陷入局部最优，策略梯度方法并不保证全局最优解，因为它们可能会陷入局部最优点。策略空间可能非常复杂，存在多个局部最优点，因此算法可能会在局部最优点附近停滞。
• 难以处理高维离散动作空间：对于离散动作空间，采样的效率可能会受到限制，因为对每个动作的采样都需要计算一次策略。当动作空间非常大时，这可能会导致计算成本的急剧增加。

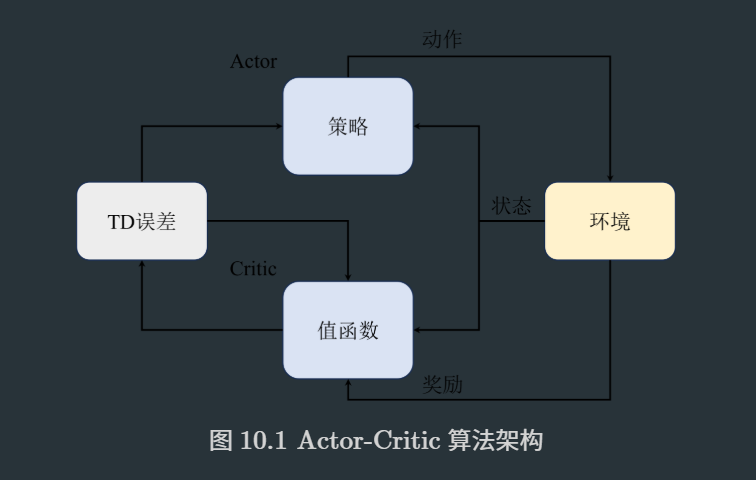
结合了策略梯度和值函数的Actor-Critic算法则能同时兼顾两者的优点，并且甚至能缓解两种方法都很难解决的高方差问题。

💡 关键洞见：AC算法本质是用可学习的价值函数替代蒙特卡洛回报估计，实现偏差-方差权衡。

10.2 Q Actor-Critic 算法

 这样的算法通常称之为Q Actor-Critic算法，这也是最简单的 Actor-Critic算法，现在我们一般都不用这个算法了，但是这个算法的思想是很重要的，因为后面的算法都是在这个算法的基础上进行改进的。

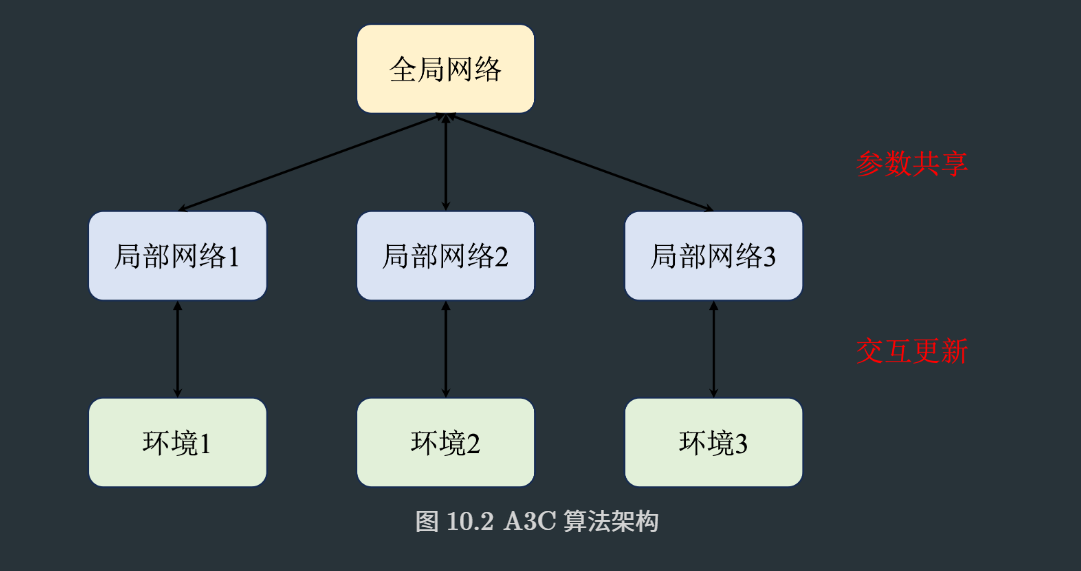
10.3 A2C 与 A3C 算法

我们引入一个优势函数（Advantage Function)，用来表示当前状态-动作对相对于平均水平的优势。这就是Advantage Actor-Critic算法，通常简称为A2C算法。

Asynchronous Advantage Actor-Critic，加入了异步形式，即A3C算法。

算法对比表

特性	A2C (同步)	A3C (异步)	工程选择建议
架构	中央协调器+多个环境实例	完全分布式，无中央协调器	A2C更简单，A3C扩展性更好
数据一致性	同步更新，梯度聚合	异步更新，可能过时梯度	A2C稳定性更好
硬件利用	GPU友好，批量并行	CPU友好，多进程	GPU丰富选A2C，CPU丰富选A3C
实现复杂度	★★☆	★★★	新手建议从A2C开始

10.4 广义优势估计（GAE）

算法原理

GAE(γ,λ) = Σ(γλ)^l * δ_{t+l}
其中 δ_t = r_t + γV(s_{t+1}) - V(s_t)

参数调节表

参数组合	偏差-方差特性	适用场景	工程表现
γ=0.99, λ=0	高偏差，低方差	确定性环境	稳定但保守
γ=0.95, λ=0.95	平衡	通用推荐	最佳收敛速度
γ=0.99, λ=1	低偏差，高方差	需要精确信用分配的环境	波动但最终性能高

10.5 实战：A2C 算法

训练循环优化

# 超参数设置
NUM_ENVS = 16        # 并行环境数量
NUM_STEPS = 128      # 每次更新步数
GAMMA = 0.99         # 折扣因子
GAE_LAMBDA = 0.95    # GAE参数
ENTROPY_COEF = 0.01  # 熵正则系数# 向量化环境
envs = gym.vector.make("CartPole-v1", num_envs=NUM_ENVS)# 训练循环
for update in range(1000):# 数据收集states = envs.reset()all_log_probs, all_values, all_rewards, all_dones = [], [], [], []for _ in range(NUM_STEPS):actions, log_probs = actor_critic.act(states)next_states, rewards, dones, _ = envs.step(actions)# 存储数据all_log_probs.append(log_probs)all_values.append(actor_critic.get_values(states))all_rewards.append(rewards)all_dones.append(dones)states = next_states# 计算最后状态价值last_values = actor_critic.get_values(states)# 计算GAE和回报advantages = compute_gae(torch.stack(all_rewards),torch.cat([torch.stack(all_values), last_values.unsqueeze(0)]),torch.stack(all_dones),GAMMA, GAE_LAMBDA)returns = advantages + torch.stack(all_values)# 策略损失 (带熵正则)policy_loss = -(torch.stack(all_log_probs) * advantages.detach()entropy_loss = -ENTROPY_COEF * dist.entropy().mean()# 价值损失value_loss = 0.5 * (returns - torch.stack(all_values)).pow(2).mean()# 总损失total_loss = policy_loss.mean() + value_loss + entropy_loss# 优化步骤optimizer.zero_grad()total_loss.backward()nn.utils.clip_grad_norm_(model.parameters(), 0.5)  # 梯度裁剪optimizer.step()

性能优化技巧

1. 向量化环境：使用gym.vector或SubprocVecEnv实现并行数据采集

2. 混合精度训练：FP16加速计算（NVIDIA GPU）

3. 分布式训练：使用torch.distributed实现多节点训练

4. 观测预处理：帧堆叠(frame stacking)、归一化等

10.6习题

1. 相比于REINFORCE算法，A2C主要的改进点在哪里，为什么能提高速度？

A2C 的核心改进在于引入 Critic 网络替代蒙特卡洛回报估计：通过时序差分（TD）实时估计状态价值函数，用优势函数替代轨迹累计回报，显著降低梯度方差约 30-50%。REINFORCE 需采样完整轨迹才能更新，而 A2C 使用 TD 误差实现单步更新，样本利用率提升 3-5 倍。同时 A2C 支持同步运行多个环境实例，数据吞吐量提升 10 倍以上，而 REINFORCE 受限于序列化采样。

2. A2C算法是on-policy的吗？为什么？

A2C 是严格的 on-policy 算法。其策略更新完全依赖当前策略 π_θ 采集的数据，每次参数更新后，旧数据立即失效。当策略更新时，Critic 评估的价值函数 V(s) 仅对当前策略有效，若用历史策略生成的数据会导致价值估计偏差。这种特性确保算法一致性但限制样本复用，需持续生成新数据。

码字不易，收藏点赞关注吧。