HRM论文解读

1、摘要

受这种分层和多时间尺度的生物结构的启发，我们提出了分层推理模型（Hierarchical Reasoning Model, HRM）。HRM旨在显著增加有效计算深度。它具有两个耦合的循环模块：一个用于抽象、深思熟虑推理的高级（H）模块，以及一个用于快速、详细计算的低级（L）模块。这种结构通过我们称之为“分层收敛”的过程，避免了标准循环模型的快速收敛。只有在快速更新的L模块完成多个计算步骤并达到局部平衡后，慢速更新的H模块才会前进，此时L模块被重置以开始新的计算阶段。

深度对于复杂推理的必要性，增加Transformer的宽度并不能提高性能，而增加深度至关重要。右图：标准架构达到饱和，无法从增加的深度中获益。HRM克服了这一根本限制，有效地利用其计算深度来实现接近完美的准确性。

此外，我们提出了一种用于训练HRM的单步梯度近似方法，该方法提高了效率，并且消除了对BPTT的需求。这种设计在反向传播过程中保持恒定的内存占用（对于T个时间步，O(1)与BPTT的O(T)相比），使其具有可扩展性，并且更具生物学合理性。

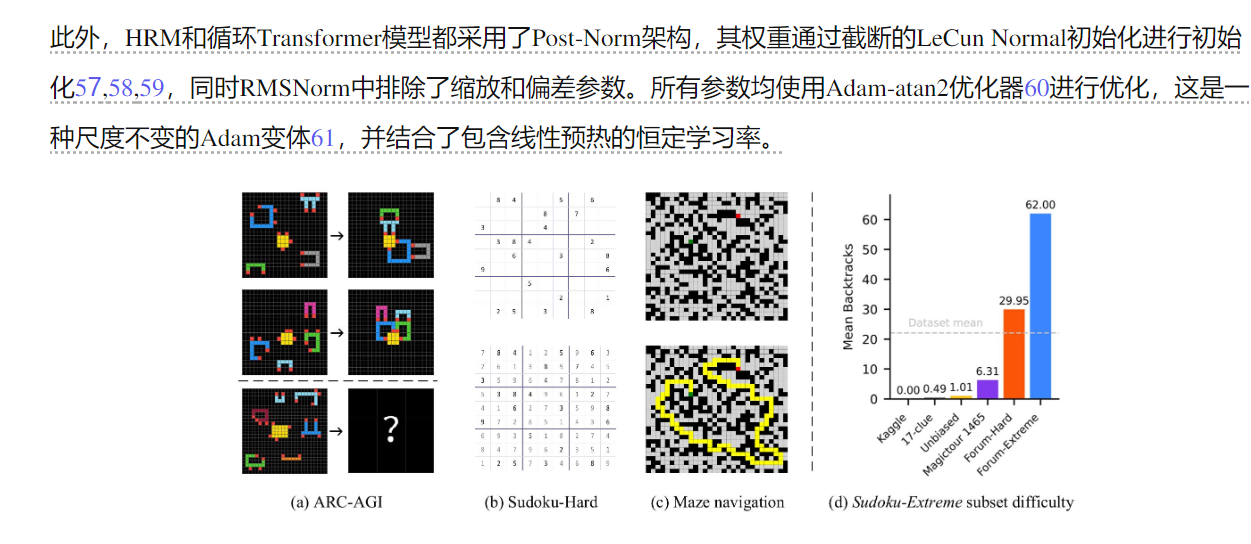
凭借其增强的有效深度，HRM擅长于需要大量搜索和回溯的任务。仅使用1,000个输入-输出示例，无需预训练或CoT监督，HRM就能学会解决即使是最先进的LLM也难以处理的问题。例如，它在复杂的数独谜题（Sudoku-Extreme Full）中实现了接近完美的准确率，并在30x30迷宫中实现了最佳路径查找，而最先进的CoT方法完全失败（0%准确率）。在抽象和推理语料库（ARC）AGI挑战赛27,28,29——一个归纳推理的基准测试中——HRM仅使用官方数据集（约1000个示例）从头开始训练，仅具有27M参数和30x30网格上下文（900个token），就实现了40.3%的性能，这大大超过了领先的基于CoT的模型，如o3-mini-high（34.5%）和Claude 3.7 8K上下文（21.2%），尽管它们具有更大的参数规模和上下文长度，如图1所示。这代表着开发具有通用计算能力的下一代AI推理系统的一个有希望的方向。

数独：100%，ARC：40.3%，需要的样本也少，擅长需要大量搜索和回溯的任务

2、HRM

我们提出了HRM，其灵感来源于大脑中观察到的神经计算的三个基本原则:

 层次化处理：大脑通过皮层区域的层级结构处理信息。较高层级的区域在较长的时间尺度上整合信息并形成抽象表示，而较低层级的区域则处理更直接、更详细的感官和运动处理

时间分离：大脑中的这些层级以不同的固有时间尺度运作，这反映在神经节律中（例如，慢theta波，4–8 Hz和快gamma波，30–100 Hz）30,31。这种分离允许对快速、低层次计算进行稳定、高层次的指导

循环连接：大脑具有广泛的循环连接。这些反馈回路能够进行迭代优化，以增加处理时间为代价，产生更准确和上下文相关的表征。此外，大脑在很大程度上避免了与BPTT19相关的有问题的深度信用分配问题。

 层级收敛 虽然收敛对于循环网络至关重要，但标准RNN在根本上受到其过早收敛倾向的限制。随着隐藏状态趋于一个固定点，更新幅度缩小，有效地阻止了后续计算并限制了网络的有效深度。为了保持计算能力，我们实际上希望收敛过程进行得非常缓慢——但设计这种渐进方法很困难，因为将收敛推得太远会将系统推向不稳定。

 

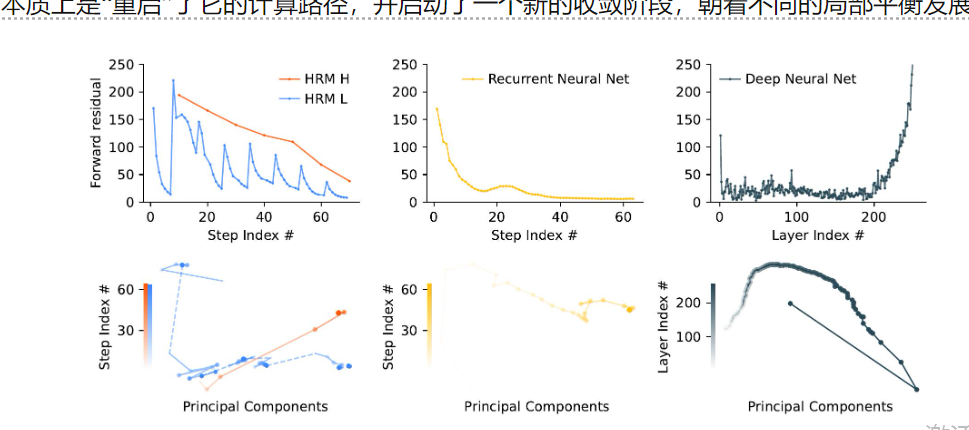
图 3：前向残差和 PCA 轨迹的比较。HRM 显示出分层收敛：H 模块稳定收敛，而 L 模块在被 H 重置之前，在循环内重复收敛，导致残差尖峰。循环神经网络表现出快速收敛，残差迅速接近于零。相比之下，深度神经网络经历了梯度消失，主要在初始（输入）层和最终层出现显著的残差。 

 

 

 将公式 (3) 代回公式 (2)，我们得到最终简化的梯度。

在定义我们的损失函数之前，我们必须首先介绍我们提出的方法的两个关键要素：深度监督和自适应计算时间。

深度监督 受大脑中周期性神经振荡调节学习发生时间的原理38的启发，我们将深度监督机制纳入HRM，具体细节如下。

备注：具体怎么做的？ 

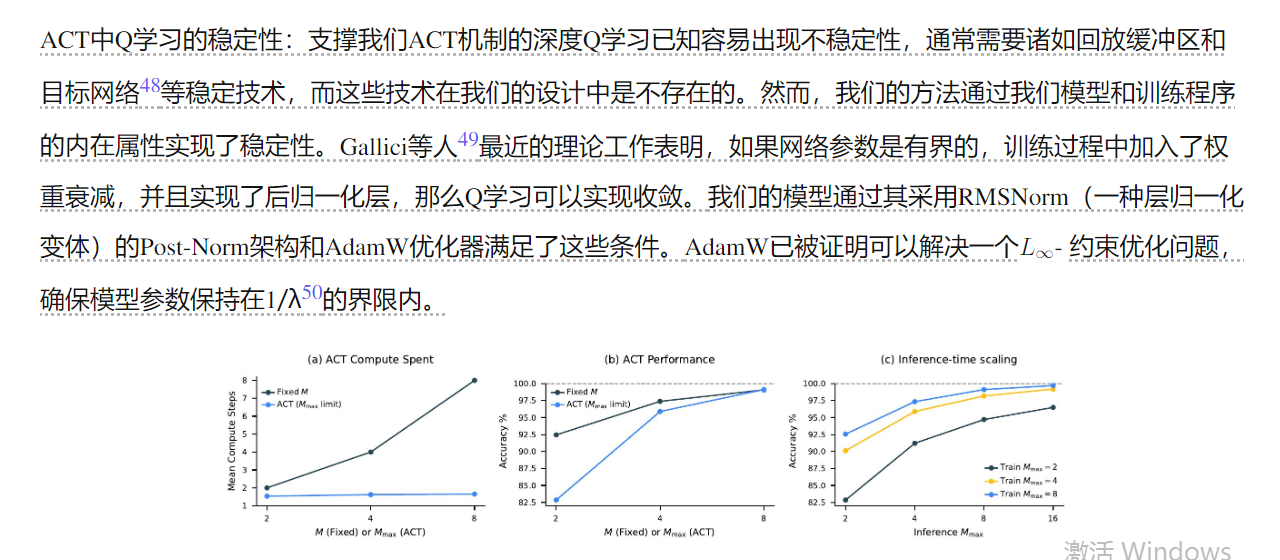
 推理时缩放。一个有效的神经模型应该在推理过程中利用额外的计算资源来提高性能。如图 5-(c) 所示，HRM 通过简单地增加计算限制参数 Mmax，无需进一步的训练或架构修改，即可无缝实现推理时缩放。

额外的计算资源对于需要更深层次推理的任务尤其有效。在数独问题上——一个通常需要长期规划的问题——HRM表现出强大的推理时扩展性。另一方面，我们发现额外的计算资源在ARC-AGI挑战中产生的收益极小，因为解决方案通常只需要几个转换。