【剑斩OFFER】算法的暴力美学——【模板】前缀和

一、题目描述

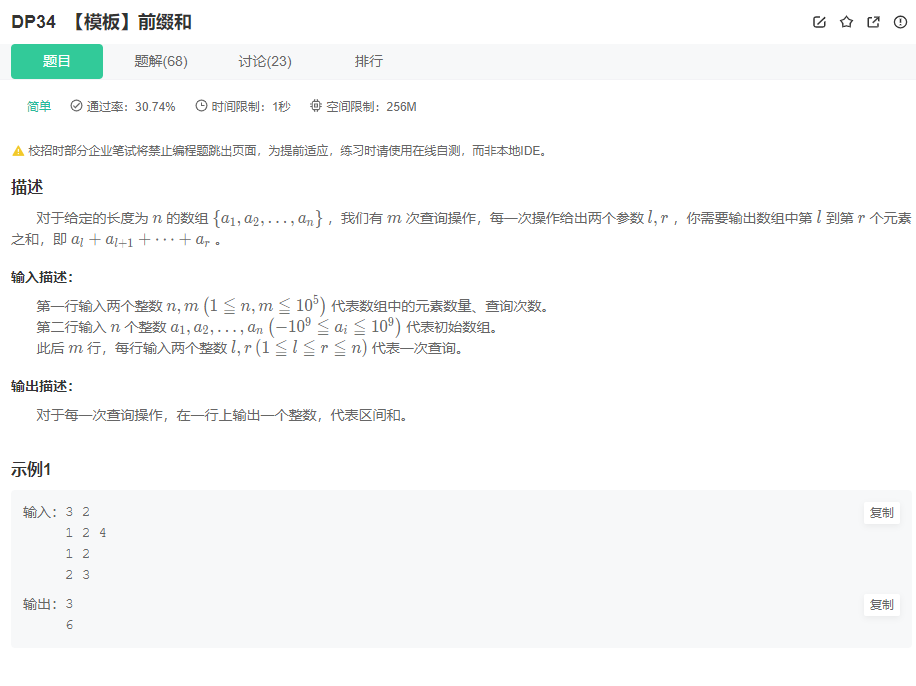
二、算法原理

一般来说我们看到这道题目是直接根据要求：求 l 到 r 的和，我们是直接遍历数组的要进行求和操作就行，但是这种方法的复杂度为：O（n）

我们使用的动态规划来解决这到题目的时间复杂度为：O（1）。

动态规划的数组必须要多添加一个元素：0 进去，放到数组的第一个元素，至于原因是为了防止越界情况的出现。

那么我们把原数组变成动态规划的数组呢？

例如我们要求：

等于：

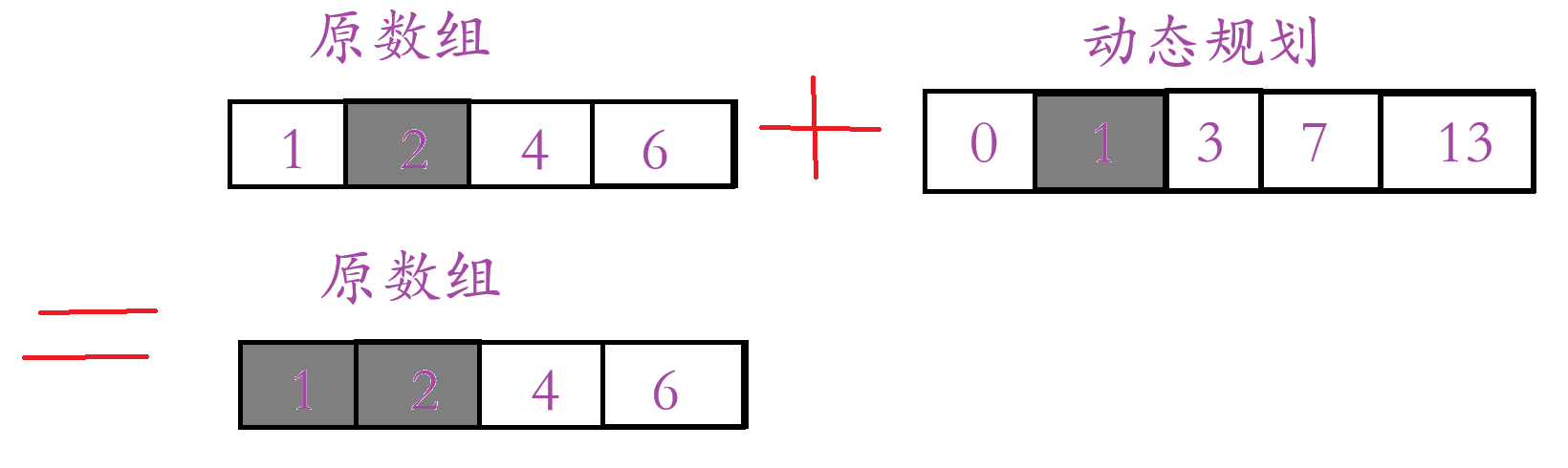
总结：arr ：原数组，new：动态规划的数组；

new[ x ] = arr[ x -1 ] + new[ x - 1]

当我们要求：

如果没有前面的0，就会越界，所以这就是我们要往前面添加个0的原因。

那么怎么使用这个动态规划来解决这道题目呢？
假设我们要求这个区域的和：

等于：

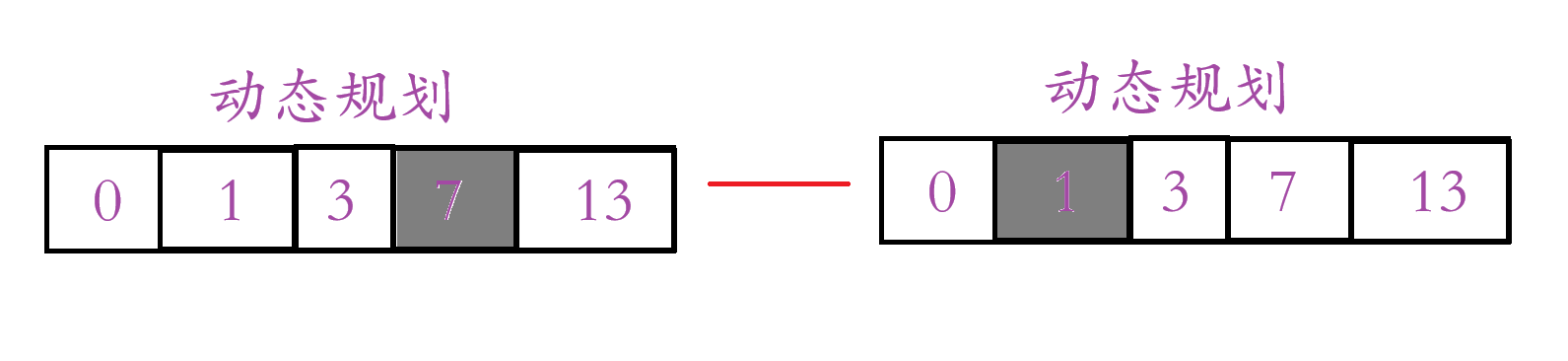
总结：l 到 r 区域的和 = new[ r ] - new[ l -1 ] 

这个时间的复杂度为O（1），比直接查找快多了。

三、代码实现

#include <iostream>
#include <vector>
using namespace std;int main()
{int n,m;//:n:数据个数，m:查找次数cin >> n >> m;vector<long long> v1;v1.push_back(0);for(int i = 1; i <= n; i++)//动态规划{long long tmp;cin >> tmp;v1.push_back(tmp + v1[i-1]);}for(int i = 0; i < m; i++)//部分区域值的计算{long long l,r;cin >> l >> r;long long  ret = v1[r] - v1[l-1];cout << ret << endl;}return 0;
}