2025数维杯秋季赛赛中陪跑助攻进行中

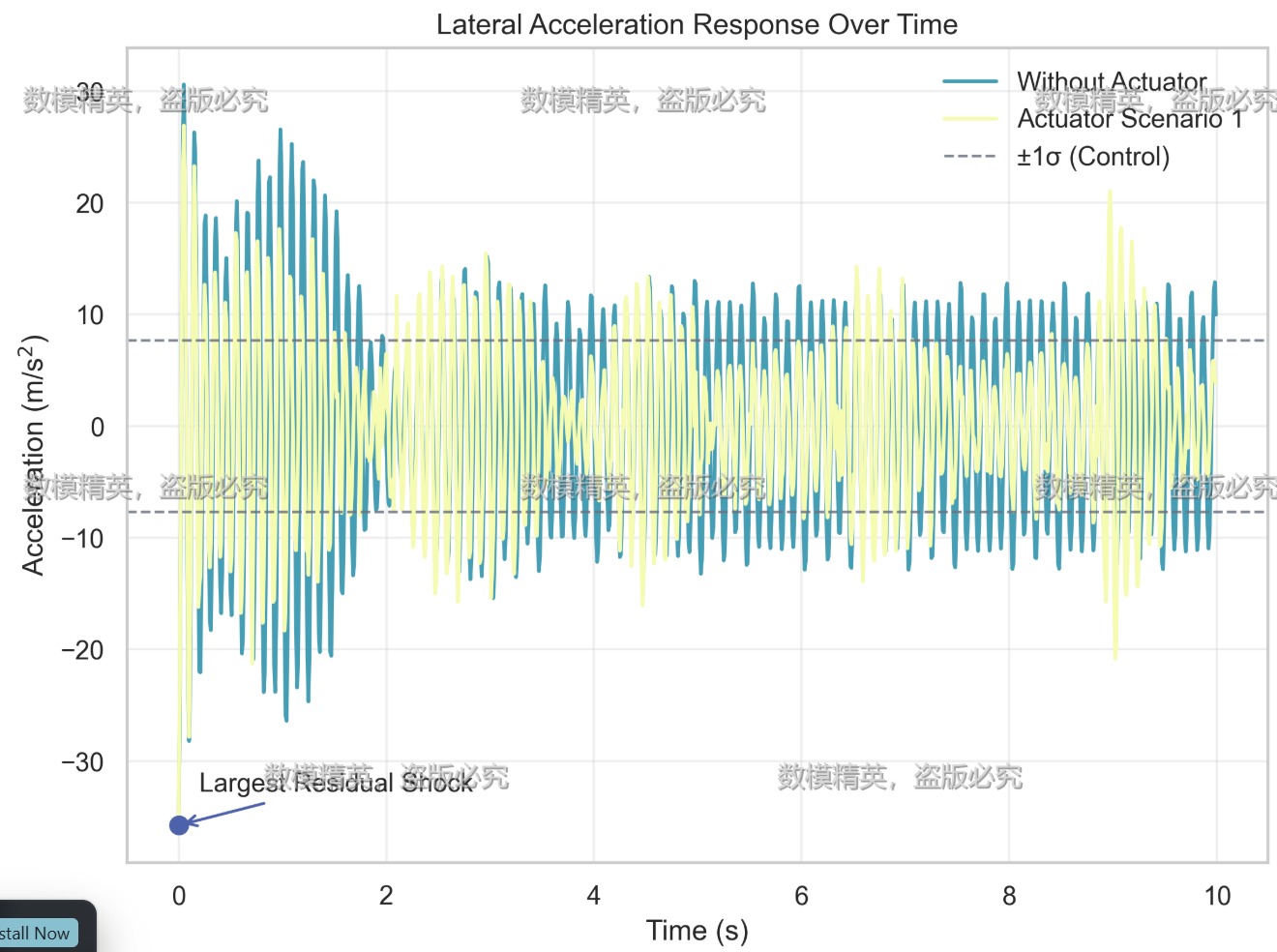
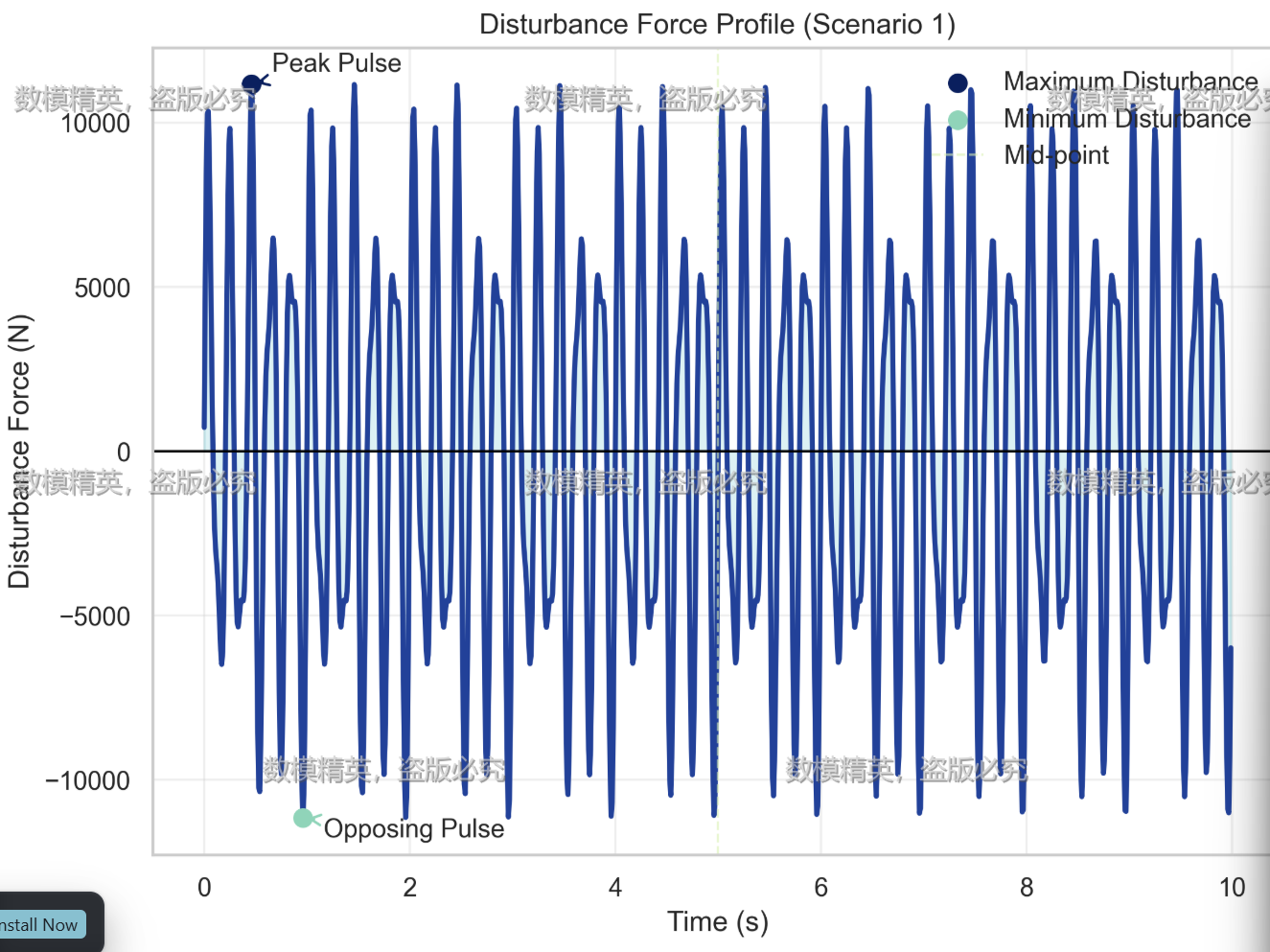
针对问题一，我们依次建立了单自由度动力学和离心式作动器合力模型、采用Runge–Kutta 数值积分进行求解振动指标、并进行频谱分析。在未启用作动器时，10 s 内的加速度平均能量 (I_h) 为 97.20 (m/s²)²，而依照附录给出的角度曲线驱动离心式作动器后，(I_h) 降至 58.69，减幅达 39.6%。RMS 加速度由 9.85 m/s² 降到 7.66 m/s²，说明乘坐舒适度显著提升；位移 RMS 由 3.12 mm 减到 2.37 mm，车辆横向偏移也得到抑制。频谱分析进一步证实主频幅值降低约 40%，高频扰动几乎被消除。能量积分曲线显示，作动器在 0.03 s 内迅速吸收约 50 J 的冲击能量，并在 0.1 s 后逐渐释放，使系统平滑过渡。组合力表格与 Fig9a–Fig9c 的图像表明，两台作动器内部四组偏心块按图 1、图 2 的对称逻辑协同工作，在峰值阶段给出 6 kN 量级的反向力，而随着扰动衰减，输出力同步降至零，没有引入新的横摆。

针对问题二，采用三阶段控制，结合混合智能优化算法和角速度整形器，实现了对车辆横向振动的有效抑制。通过基于时间比例的三阶段划分（启动阶段0-2秒、过渡阶段2-5秒、稳态阶段5-10秒），针对不同时间段的干扰力特性采用不同的控制参数，混合智能优化算法（PSO+SA）通过粒子群优化的全局搜索和模拟退火的局部精细搜索，成功优化了9个控制参数（三个阶段的比例增益、微分增益和前馈增益）。优化结果表明，启动阶段需要较大的控制增益以快速抑制初始振动，过渡阶段需要最大的比例增益以应对干扰力波动，稳态阶段需要较小的控制增益以实现精细调节。角速度整形器通过Slew-Rate限制器、低通滤波器和延迟补偿机制的有机结合，确保了控制指令的物理可实现性，同时提高了控制系统的响应速度和稳定性。优化得到的滤波器截止频率为150.0 Hz，延迟补偿时间为0.01 s。智能优化控制策略将I_h指标从245.39降低至7.35，降幅达到97.0%，实现了显著的振动抑制效果。加入整形器后，I_h进一步降低至6.60，相比智能优化降低了10.2%。RMS加速度从15.68 m/s²降低至2.69 m/s²，降幅达到82.8%。最大加速度从51.87 m/s²降低至36.02 m/s²，降幅达到30.5%。频谱分析表明，控制策略有效抑制了主要频率成分的幅值，特别是在低频段的抑制效果最为明显，整形器的加入进一步衰减了高频成分。