Opencv(十二):图像矫正

思维导图

前言

在机器视觉领域，图像矫正技术是解决视角畸变问题的关键手段。无论是自动驾驶中的车道线识别、文档扫描后的倾斜校正，还是工业检测中的目标定位，都离不开图像矫正技术的支撑。而透视变换作为图像矫正的核心原理，能够有效修正因拍摄角度导致的物体形变，让图像中的目标呈现更符合人眼直观感受的视角。

一、透视变换的核心概念与原理

1.1 透视变换与仿射变换的区别

要理解透视变换，首先需要明确其与常见的仿射变换的差异。仿射变换是将二维坐标系转换到另一二维坐标系的线性变换，仅包含旋转和平移操作，核心特点是保持图形的平行性——即平行四边形经过仿射变换后依然是平行四边形。但在现实场景中，我们观察物体时会受到"近大远小"的透视效果影响，比如从斜上方拍摄的车道线，会呈现出远端收缩的梯形形态，这种畸变仅靠仿射变换无法修正。

透视变换（又称单应性变换）则突破了线性变换的限制，它是将图像投影到新视平面的过程，本质是三维空间到二维平面的投影转换。其核心优势在于能够处理透视畸变，不仅保持直线的共线性（直线经过变换后依然是直线），还能改变物体的观察视角。例如，将平视视角下的倾斜车道线，通过透视变换转换为俯视视角的平行车道线，这正是图像矫正的核心目标。

1.2 透视变换的直观作用

透视变换的本质的是改变图像中目标物体的观察视角。在实际应用中，透视变换的作用主要体现在两个方面：

• 视角矫正：将倾斜视角转换为正射视角，如把斜拍的文档转换为正上方拍摄的正视效果；
• 畸变修正：消除"近大远小"导致的图形形变，如将梯形的车道线区域修正为平行的矩形区域。

简单来说，透视变换就像是给图像换了一个观察角度，让原本因拍摄位置限制而畸变的目标，以更规整的形态呈现，为后续的图像分析和识别提供便利。

二、透视变换的数学模型与公式推导

2.1 透视变换矩阵的定义

透视变换的实现依赖于3×3的透视变换矩阵，该矩阵是连接原始图像坐标与变换后图像坐标的核心桥梁。其数学表达式如下：

其中：

• (x, y) 是原始图像中像素点的二维坐标；
• 3×3矩阵中的元素 ( a11) 至 ( a33) 是变换参数，包含旋转量、平移量等关键信息；
• (X, Y, Z) 是变换后的三维中间坐标，通过后续归一化得到二维图像坐标。

2.2 坐标转换公式推导

透视变换的核心是通过矩阵运算将原始坐标 ( (x, y) ) 转换为目标坐标 ( (x’, y’) )，具体推导过程如下：

1. 矩阵乘法展开：
   根据上述矩阵运算规则，将三维中间坐标展开为具体表达式：
   

2. 二维坐标归一化：
   由于透视变换涉及三维投影到二维的过程，需要通过除以中间变量 ( Z ) 进行归一化，得到最终的二维目标坐标：
   

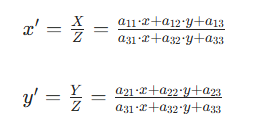
这里需要注意的是，透视变换矩阵的推导涉及三维空间到二维平面的投影转换，过程较为复杂，但在实际应用中无需手动计算矩阵元素，可通过工具函数自动生成，核心是理解坐标转换的逻辑。

2.3 矩阵参数的物理意义

透视变换矩阵的9个参数可分为三个功能模块，分别对应不同的变换效果：

• 左上角2×2子矩阵
  ：主要控制图像的旋转和缩放；
• 第一列和第二列的最后一个元素 (a31)、( a32)：控制透视畸变的程度，是实现"近大远小"修正的关键参数；
• 第三列前两个元素 (a13)、( a23})：控制图像的平移，即整体位置的偏移；
• 右下角元素 (a33)：通常设为1，用于维持坐标归一化的尺度。

这些参数的组合作用，使得透视变换能够灵活调整图像的视角和形态，从而实现精准的图像矫正。

三、OpenCV透视变换核心函数解析

在实际开发中，OpenCV提供了两个核心函数用于实现透视变换，分别是生成透视变换矩阵的getPerspectiveTransform()和执行透视变换的warpPerspective()。下面将详细解析这两个函数的参数、功能和使用场景。

3.1 getPerspectiveTransform()函数

该函数的作用是根据原始图像和目标图像的对应点，生成3×3的透视变换矩阵。

函数语法

cv2.getPerspectiveTransform(src, dst)

参数详解

• src：原始图像中待变换区域的四个顶点坐标，数据类型为np.float32，格式为[[x1,y1], [x2,y2], [x3,y3], [x4,y4]]。这四个点需构成一个四边形，通常选择目标物体的边界角点（如文档的四个角、车道线的四个端点）。
• dst：目标图像中对应的四个顶点坐标，数据类型同样为np.float32。这四个点定义了原始四边形变换后的形状，通常设置为规则的矩形（如[[0,0], [width,0], [width,height], [0,height]]），以实现矫正效果。

返回值

返回一个3×3的numpy数组，即透视变换矩阵M，可直接用于后续的warpPerspective()函数。

使用注意事项

• 四个对应点的顺序必须一致，如均按"左上→右上→右下→左下"的顺时针顺序排列，否则会导致变换后的图像错乱；
• 原始图像的四个点不能共线，需构成凸四边形，否则无法生成有效的透视变换矩阵；
• 坐标值需为浮点数类型，即使是整数坐标，也需转换为np.float32格式。

3.2 warpPerspective()函数

该函数的作用是利用生成的透视变换矩阵，对输入图像执行透视变换，得到矫正后的图像。

函数语法

cv2.warpPerspective(src, M, dsize, flags=None, borderMode=None)

参数详解

• src：输入图像，即需要进行矫正的原始图像，可通过cv2.imread()函数读取；
• M：透视变换矩阵，由getPerspectiveTransform()函数生成；
• dsize：输出图像的尺寸，格式为(width, height)（注意是宽度在前、高度在后），通常根据目标场景需求设置，如文档矫正可设置为(800, 1000)；
• flags：插值方法标记，用于控制图像变换过程中的像素插值方式，常用取值如下：
  • cv2.INTER_NEAREST：最近邻插值，速度最快但效果较差；
  • cv2.INTER_LINEAR：双线性插值，兼顾速度和效果，默认值；
  • cv2.INTER_CUBIC：双三次插值，效果较好但速度较慢；
  • cv2.INTER_LANCZOS4： Lanczos插值，适用于图像放大，效果最优；
• borderMode：边界填充模式，用于处理变换后图像边界的空白区域，常用取值为cv2.BORDER_CONSTANT（常量填充）和cv2.BORDER_REPLICATE（复制边界像素填充），默认值为cv2.BORDER_REFLECT（反射填充）。

返回值

返回矫正后的图像，数据类型为numpy数组，可通过cv2.imshow()显示或cv2.imwrite()保存。

3.3 函数组合使用逻辑

透视变换的实现流程本质是"定义对应点→生成矩阵→执行变换"的三步法，两个核心函数的组合使用逻辑如下：

1. 先通过人工标注或自动检测，获取原始图像中待矫正区域的四个顶点坐标（src）；
2. 定义这四个顶点在目标图像中的理想坐标（dst），通常为规则矩形；
3. 调用getPerspectiveTransform(src, dst)生成透视变换矩阵M；
4. 调用warpPerspective(src_img, M, dsize)执行变换，得到矫正后的图像。

这种组合方式能够快速实现精准的图像矫正，适用于大多数机器视觉场景。

四、图像矫正实战

4.1 代码实现与优化

完整代码示例

#导入opencv库,方便调用函数
import cv2
import numpy as np
#1.读取图片
image_np = cv2.imread('./test.png')
#获取图像大小
img_shape = image_np.shape#2.定义原始图像中四个顶点的坐标
points1 = np.float32([[210,115],[685,170],[135,400],[650,460]])
#定义目标图像中,这四个顶点坐标所对应得位置
points2 = np.float32([[0,0],[img_shape[1],0],[0,img_shape[0]],[img_shape[1],img_shape[0]]])cv2.line(image_np, points1[0].astype(np.int64).tolist(),points1[1].astype(np.int64).tolist(),(0,0,255),1,lineType=cv2.LINE_AA)
cv2.line(image_np, points1[0].astype(np.int64).tolist(),points1[2].astype(np.int64).tolist(),(0,0,255),1,lineType=cv2.LINE_AA)
cv2.line(image_np, points1[3].astype(np.int64).tolist(),points1[1].astype(np.int64).tolist(),(0,0,255),1,lineType=cv2.LINE_AA)
cv2.line(image_np, points1[3].astype(np.int64).tolist(),points1[2].astype(np.int64).tolist(),(0,0,255),1,lineType=cv2.LINE_AA)#3.获取透视变换矩阵
M = cv2.getPerspectiveTransform(points1,points2)#得到透视变换矩阵#4.进行透视变换
image_warp = cv2.warpPerspective(image_np,M,(img_shape[1],img_shape[0]))#5.显示
cv2.imshow('image_np',image_np)
cv2.imshow('image_warp',image_warp)
cv2.waitKey(0)

输出结果为:

五、总结与进阶学习建议

5.1 核心知识点总结

本文围绕图像矫正的核心技术——透视变换，从原理、数学模型、工具函数到实战应用进行了全面解析，核心知识点如下：

1. 透视变换是处理透视畸变的关键技术，能够改变图像的观察视角，区别于保持平行性的仿射变换；
2. 透视变换的数学核心是3×3变换矩阵，通过坐标归一化实现原始坐标到目标坐标的转换；
3. OpenCV的getPerspectiveTransform()和warpPerspective()是实现透视变换的核心工具，需掌握参数配置和使用场景；
4. 实战中需注意坐标顺序、图像路径、插值方法等关键细节，避免常见错误。

图像矫正技术是机器视觉的基础，掌握透视变换的核心原理和实战技巧，能够为后续的图像分析、目标识别等高级应用打下坚实的基础。通过不断的实践和进阶学习，可逐步提升对复杂场景的处理能力，应对更多实际工程问题。