当前位置：首页 > news >正文

算法基础篇：（七）基础算法之二分算法 —— 从 “猜数字” 到 “解难题” 的高效思维

news 2025/11/13 6:20:22

前言

在算法世界里，有这样一种神奇的算法：它能把复杂的搜索问题从 “大海捞针” 变成 “精准定位”，把 O (n) 的时间复杂度直接压缩到 O (log n)。它就是二分算法 —— 一个看似简单却暗藏玄机，既能解决基础搜索问题，又能攻克 “最大值最小”“最小值最大” 等进阶难题的核心算法。今天，我们就从 “猜数字” 游戏出发，一步步揭开二分算法的神秘面纱，从原理到模板，从基础应用到进阶实战，带你彻底掌握这种高效的算法。下面就让我们正式开始吧！

一、二分算法是什么？—— 从 “猜数字” 理解核心思想

1.1 生活中的二分：猜数字游戏

相信大家都玩过 “猜数字” 的游戏：裁判心里想一个 1-100 的整数，玩家每次猜一个数，裁判只会回答 “大了”“小了” 或 “猜对了”。那么我们应该如何最快猜对？

暴力玩法：从 1 开始依次猜，最坏情况要猜 100 次（时间复杂度 O (n)）。
二分玩法：每次猜中间数 —— 第一次猜 50，若 “大了” 就猜 25，若 “小了” 就猜 75，每次排除一半范围。最坏情况只需 7 次（log₂100≈6.64），这就是二分的核心逻辑！

二分算法的本质的是利用 “二段性” 缩小搜索范围：把整个解空间分成两部分，每次排除掉不可能包含答案的部分，只在可能包含答案的部分继续搜索，直到找到答案。

1.2 算法中的二分：必须满足 “二段性”

不是所有问题都能用二分解决，它有一个严格前提 ——解空间具有 “二段性”。什么是二段性？

简单来说：存在一个 “分界点”，使得分界点左边的所有元素都满足某个条件，右边的所有元素都不满足（或反之）。例如：

有序数组中找目标值：分界点是目标值，左边元素≤目标值，右边元素≥目标值。
木材加工问题：分界点是 “最大可切割长度”，长度≤分界点时能切出足够段数，长度 > 分界点时切不出足够段数。

没有二段性的问题，比如 “找无序数组中的任意一个峰值”（可能存在多个不连续的峰值），就不能直接用二分解决。

1.3 二分的两种经典场景

根据问题类型，二分主要分为两大类，也是面试和竞赛的高频考点：

二分查找：在有序数组中查找目标值的位置（如找第一个≥目标值的元素、最后一个≤目标值的元素）。
二分答案：把 “求最优解” 转化为 “判断某个值是否为可行解”，通过二分可行解空间找到最优解（如 “最大值最小”“最小值最大” 问题）。

接下来，我们会分别深入这两大场景，结合具体例题讲解实现思路。

二、二分算法的核心模板 —— 告别 “边界恐惧”

很多人学二分最怕 “边界处理”：到底是left = mid还是left = mid + 1？到底是while(left < right)还是while(left <= right)？其实，只要掌握一套固定模板，就能轻松应对 99% 的二分问题。

2.1 为什么需要统一模板？

网上的二分模板是五花八门的，但它们的核心差异其实在于 “如何处理中间值 mid 与边界的关系”。如果每次都临时推导，很容易在边界条件上出错（比如漏判、死循环）。我们只需要记住两套模板：一套用于 “找左边界”，一套用于 “找右边界”，就能覆盖所有二分场景。

2.2 模板 1：找左边界（第一个满足条件的元素）

适用场景：找有序数组中第一个≥目标值的元素、第一个满足条件的位置（如 “第一个大于 x 的元素”）。

模板逻辑

初始范围：left = 0，right = n - 1（数组下标从 0 开始）。
计算 mid：mid = left + (right - left) / 2（避免left + right溢出）。
判断条件：若check(mid)为真（当前 mid 满足条件），说明答案在左半部分，收缩右边界：right = mid；若为假，说明答案在右半部分，扩展左边界：left = mid + 1。
循环结束：left == right，此时 left 就是左边界。

代码模板

// 找左边界：第一个满足 check(mid) 的元素（数组下标从0开始）
int findLeftBound(vector<int>& nums, int target) {int n = nums.size();int left = 0, right = n - 1;while (left < right) { // 循环结束时 left == rightint mid = left + (right - left) / 2;if (check(mid)) { // check：判断mid是否满足目标条件right = mid; // 答案在左半部分，收缩右边界} else {left = mid + 1; // 答案在右半部分，扩展左边界}}// 最后需判断left是否真的满足条件（防止目标值不存在）return check(left) ? left : -1;
}

示例：找第一个≥target 的元素

比如数组[1,3,5,7,9]，target=4，第一个≥4 的元素是 5（下标 2）。用模板实现：

bool check(int mid, vector<int>& nums, int target) {return nums[mid] >= target; // 条件：当前元素≥目标值
}int findFirstGe(vector<int>& nums, int target) {int n = nums.size();int left = 0, right = n - 1;while (left < right) {int mid = left + (right - left) / 2;if (check(mid, nums, target)) {right = mid;} else {left = mid + 1;}}return nums[left] >= target ? left : -1; // 防止target比所有元素大
}

2.3 模板 2：找右边界（最后一个满足条件的元素）

适用场景：找有序数组中最后一个≤目标值的元素、最后一个满足条件的位置（如 “最后一个小于 x 的元素”）。

模板逻辑

初始范围：left = 0，right = n - 1。
计算 mid：mid = left + (right - left + 1) / 2（关键！加 1 是为了避免死循环）。
判断条件：若check(mid)为真，说明答案在右半部分，扩展左边界：left = mid；若为假，说明答案在左半部分，收缩右边界：right = mid - 1。
循环结束：left == right，此时 left 就是右边界。

代码模板

// 找右边界：最后一个满足 check(mid) 的元素（数组下标从0开始）
int findRightBound(vector<int>& nums, int target) {int n = nums.size();int left = 0, right = n - 1;while (left < right) { // 循环结束时 left == rightint mid = left + (right - left + 1) / 2; // 加1避免死循环if (check(mid)) { // check：判断mid是否满足目标条件left = mid; // 答案在右半部分，扩展左边界} else {right = mid - 1; // 答案在左半部分，收缩右边界}}// 最后需判断left是否真的满足条件（防止目标值不存在）return check(left) ? left : -1;
}

示例：找最后一个≤target 的元素

比如数组[1,3,5,7,9]，target=4，最后一个≤4 的元素是 3（下标 1）。用模板实现：

bool check(int mid, vector<int>& nums, int target) {return nums[mid] <= target; // 条件：当前元素≤目标值
}int findLastLe(vector<int>& nums, int target) {int n = nums.size();int left = 0, right = n - 1;while (left < right) {int mid = left + (right - left + 1) / 2; // 关键：加1if (check(mid, nums, target)) {left = mid;} else {right = mid - 1;}}return nums[left] <= target ? left : -1; // 防止target比所有元素小
}

2.4 为什么右边界模板要加 1？

这是很多人的疑问，我们用一个例子解释：假设数组[1,2]，找最后一个≤2 的元素（右边界是 1）。

若 mid 不加 1：mid = 0 + (1-0)/2 = 0，check(0)=true，则left=0，陷入left=0、right=1的死循环。
若 mid 加 1：mid = 0 + (1-0+1)/2 = 1，check(1)=true，则left=1，循环结束，正确。

加 1 的本质是 “让 mid 偏向右边”，避免当left和right相差1时，mid 始终等于 left，导致无法推进循环。

三、场景 1：二分查找 —— 有序数组中的精准定位

二分查找是二分算法的基础应用，看似简单，但实际考察的是 “对边界的理解”。除了 “找目标值是否存在”，更常考的是 “找目标值的左右边界”，比如 “第一个出现的位置”“最后一个出现的位置”。

例题 1：牛可乐和魔法封印（牛客网）—— 区间内数字个数

题目链接：https://ac.nowcoder.com/acm/problem/235558

题目描述

给定一个非严格单调递增的序列 a，以及 q 个查询（x_i, y_i），每个查询需要输出序列中≥x_i 且≤y_i 的数字个数。

输入：

第一行：n（序列长度，1≤n≤1e5）
第二行：n 个整数（-1e9≤a_i≤1e9）
第三行：q（查询次数，1≤q≤1e5）
接下来 q 行：每个查询的 x_i 和 y_i

输出：每个查询的结果（若没有符合条件的数字，输出 0）

题目分析

要计算 “≥x 且≤y” 的数字个数，只需找到两个边界：

左边界：第一个≥x 的元素位置（记为 L）
右边界：最后一个≤y 的元素位置（记为 R）
结果 = R - L + 1（若 L>R，结果为 0）

这正是我们之前讲的 “左边界模板” 和 “右边界模板” 的结合。

代码实现

#include <iostream>
#include <vector>
using namespace std;// 找左边界：第一个≥x的元素位置（下标从0开始）
int findLeft(const vector<int>& a, int x) {int n = a.size();int left = 0, right = n - 1;while (left < right) {int mid = left + (right - left) / 2;if (a[mid] >= x) {right = mid;} else {left = mid + 1;}}// 检查是否真的≥x（防止x比所有元素大）return a[left] >= x ? left : n; // 若不存在，返回n（超出数组范围）
}// 找右边界：最后一个≤y的元素位置（下标从0开始）
int findRight(const vector<int>& a, int y) {int n = a.size();int left = 0, right = n - 1;while (left < right) {int mid = left + (right - left + 1) / 2;if (a[mid] <= y) {left = mid;} else {right = mid - 1;}}// 检查是否真的≤y（防止y比所有元素小）return a[left] <= y ? left : -1; // 若不存在，返回-1（超出数组范围）
}int main() {ios::sync_with_stdio(false); // 加速输入输出cin.tie(0);int n;cin >> n;vector<int> a(n);for (int i = 0; i < n; i++) {cin >> a[i];}int q;cin >> q;while (q--) {int x, y;cin >> x >> y;int L = findLeft(a, x);int R = findRight(a, y);if (L > R) {cout << 0 << endl;} else {cout << R - L + 1 << endl;}}return 0;
}

思路总结

这道题的关键是 “将区间计数转化为两个边界的差值”，避免了暴力遍历每个查询（O (qn) 超时），最终时间复杂度是 O (n + q log n)，能轻松处理 1e5 级别的数据。

例题 2：A-B 数对（洛谷）—— 利用二分算对数

题目链接：https://www.luogu.com.cn/problem/P1102

题目描述

给定一串正整数数列和正整数 C，计算满足 A - B = C 的数对个数（不同位置的相同数字算不同数对）。

输入：

第一行：N（数列长度）和 C
第二行：N 个正整数

输出：满足条件的数对个数

题目示例

输入：4 1；1 1 2 3

输出：3（解释：(2-1)×2 + (3-2)×1 = 2+1=3）

题目分析

由 A - B = C 可得 B = A - C。因此，我们可以：

先将数组排序（排序后才能用二分）。
遍历每个 A（数组中的元素），在 A 左边的元素中找 B = A - C 的个数（用二分找 B 的左右边界，差值即为个数）。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;typedef long long LL; // 防止结果溢出int main() {ios::sync_with_stdio(false);cin.tie(0);int n, C;cin >> n >> C;vector<int> a(n);for (int i = 0; i < n; i++) {cin >> a[i];}sort(a.begin(), a.end()); // 排序是二分的前提LL res = 0;// 遍历每个A，找左边B = A - C的个数for (int i = 0; i < n; i++) {int target = a[i] - C;// 找左边界：第一个≥target的位置int L = lower_bound(a.begin(), a.begin() + i, target) - a.begin();// 找右边界：第一个>target的位置int R = upper_bound(a.begin(), a.begin() + i, target) - a.begin();res += (R - L); // 个数 = 右边界 - 左边界}cout << res << endl;return 0;
}

关键知识点：STL 中的二分函数

C++ 的<algorithm>库提供了两个二分函数，可直接用于有序数组：

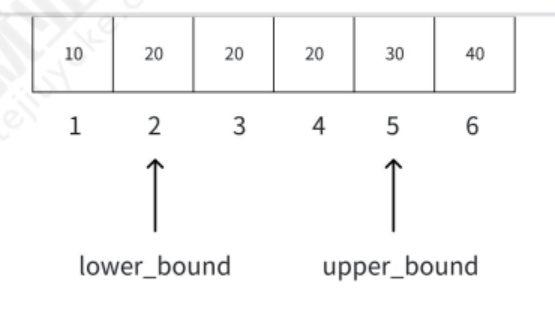
lower_bound(first, last, val)：返回第一个≥val 的元素迭代器，时间复杂度 O (log n)。
upper_bound(first, last, val)：返回第一个 > val 的元素迭代器，时间复杂度 O (log n)。

这两个函数本质上是我们之前讲的 “左边界模板” 的实现，使用时需注意：

数组必须是非递减有序的。
迭代器范围是左闭右开（[first, last)），比如a.begin() + i表示只在第 0~i-1 个元素中查找。

思路总结

这道题的核心是 “将数对问题转化为单元素查找”，通过排序 + 二分，将时间复杂度从 O (n²) 优化到 O (n log n)，避免了超时。同时，STL 的二分函数可以简化代码，但要理解其内部逻辑（本质还是我们的模板），避免过度依赖。

例题 3：烦恼的高考志愿（洛谷 P1678）—— 最小不满意度之和

题目链接：https://www.luogu.com.cn/problem/P1678

题目描述

现有 m 所学校，每所学校的预计分数线为 a_i；n 位学生，估分分别为 b_i。为每位学生推荐一所学校，要求学校分数线与学生估分的差值最小（不满意度），求所有学生不满意度之和的最小值。

输入：

第一行：m（学校数）和 n（学生数）
第二行：m 个学校的分数线
第三行：n 个学生的估分

输出：最小不满意度之和

题目示例

输入：4 3；513 598 567 689；500 600 550

输出：32（解释：500→513（差 13），600→598（差 2），550→567（差 17），总和 13+2+17=32）

题目分析

先将学校分数线排序（方便二分查找）。
对每个学生的估分 b_i，找到分数线中第一个≥b_i 的位置 pos：
可能的最优学校是 pos（分数线≥b_i）和 pos-1（分数线≤b_i）。
计算两个学校的不满意度，取较小值加入总和。

边界处理：若 pos=0（所有分数线≥b_i），则只能选 pos；若 pos=m（所有分数线≤b_i），则只能选 pos-1。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;typedef long long LL;int main() {ios::sync_with_stdio(false);cin.tie(0);int m, n;cin >> m >> n;vector<int> a(m);for (int i = 0; i < m; i++) {cin >> a[i];}sort(a.begin(), a.end()); // 排序学校分数线LL total = 0;for (int i = 0; i < n; i++) {int b;cin >> b;// 找左边界：第一个≥b的分数线位置auto it = lower_bound(a.begin(), a.end(), b);int pos = it - a.begin();int min_diff;if (pos == 0) {// 所有分数线都≥b，只能选第一个min_diff = abs(a[pos] - b);} else if (pos == m) {// 所有分数线都≤b，只能选最后一个min_diff = abs(a[pos - 1] - b);} else {// 比较pos和pos-1的差值min_diff = min(abs(a[pos] - b), abs(a[pos - 1] - b));}total += min_diff;}cout << total << endl;return 0;
}

思路总结

这道题的关键是 “对每个学生，只有两个可能的最优学校”，通过二分快速定位这两个学校，避免了对每个学生遍历所有学校（O (nm) 超时）。最终时间复杂度是 O (m log m + n log m)，高效处理 1e5 级别的数据。

四、场景 2：二分答案 ——“最大值最小” 问题的克星

二分答案是二分算法的进阶应用，也是面试中的难点。它的核心思想是 “将求最优解转化为判断可行性”—— 如果我们能判断 “某个值是否为可行解”，就能通过二分可行解空间找到最优解。

4.1 二分答案的适用场景

当问题满足以下两个条件时，就可以用二分答案：

最优解具有二段性：所有≤最优解的值都是可行解，所有 > 最优解的值都是不可行解（或反之）。
可行性判断可高效实现：判断某个值是否为可行解的时间复杂度较低（通常是 O (n) 或 O (n log n)）。

常见的二分答案场景：

木材加工：求最大可切割长度（长度越大，能切的段数越少，二段性明显）。
砍树：求伐木机的最大高度（高度越高，获得的木材越少，二段性明显）。
跳石头：求最短跳跃距离的最大值（距离越大，需要移走的石头越多，二段性明显）。

4.2 二分答案的通用步骤

确定可行解空间：找到解的最小值（left）和最大值（right）。例如：
木材加工：left=1，right = 最大木材长度。
砍树：left=1，right = 最高树木高度。

编写可行性函数：判断 “当解为 mid 时，是否满足题目要求”（如 “切割长度为 mid 时，能切出≥k 段”）。
二分查找最优解：用模板找右边界（因为要找 “最大值最小” 或 “最小值最大”，通常是右边界）。

例题 1：木材加工（洛谷 P2440）—— 入门级二分答案

题目链接：https://www.luogu.com.cn/problem/P2440

题目描述

木材厂有 n 根原木，要切割成 k 段长度均为 l 的小段（木材可剩余）。求 l 的最大值（l 为正整数），若连 1cm 的小段都切不出来，输出 0。

输入：

第一行：n（原木数量）和 k（需要的小段数）
接下来 n 行：每根原木的长度（正整数）

输出：l 的最大值

题目示例

输入：3 7；232；124；456

输出：114（解释：232/114=2，124/114=1，456/114=4，总段数 2+1+4=7）

题目分析

可行解空间：l 的最小值是 1，最大值是最大原木长度（超过这个长度，一根都切不出来）。
可行性判断：对于给定的 l，计算所有原木能切出的总段数（sum = 原木长度 //l），若 sum≥k，则 l 是可行解。
二分目标：找最大的可行解 l（右边界）。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;typedef long long LL;// 可行性函数：切割长度为mid时，能否切出≥k段
bool isPossible(const vector<LL>& logs, int k, LL mid) {if (mid == 0) return false; // 避免除以0LL total = 0;for (LL log : logs) {total += log / mid;// 剪枝：总段数已足够，无需继续计算if (total >= k) return true;}return total >= k;
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n, k;cin >> n >> k;vector<LL> logs(n);LL max_log = 0;for (int i = 0; i < n; i++) {cin >> logs[i];max_log = max(max_log, logs[i]);}// 可行解空间：left=0，right=最大原木长度LL left = 0, right = max_log;LL ans = 0;while (left < right) {LL mid = left + (right - left + 1) / 2; // 找右边界，mid加1if (isPossible(logs, k, mid)) {ans = mid; // 记录可行解left = mid; // 尝试更大的长度} else {right = mid - 1; // 长度太大，缩小范围}}// 最后判断left是否可行（防止k=0的极端情况，题目中k≥1）cout << (isPossible(logs, k, left) ? left : 0) << endl;return 0;
}

思路总结

这道题是二分答案的入门题，可行性函数简单直观。关键是理解 “为什么要找右边界”—— 因为我们要找最大的可行解，当 mid 是可行解时，需要继续在右半部分找更大的可行解；当 mid 不可行时，只能在左半部分找更小的可行解。

例题 2：砍树（洛谷 P1873）—— 经典 “最大值最小” 问题

题目链接：https://www.luogu.com.cn/problem/P1873

题目描述

伐木工人需要砍 M 米长的木材，伐木机的高度为 H，会锯掉所有树木高于 H 的部分（低于等于 H 的部分保留）。求 H 的最大整数高度，使得获得的木材≥M 米。

输入：

第一行：N（树木数量）和 M（需要的木材长度）
第二行：N 个整数（每棵树的高度）

输出：H 的最大值

题目示例

输入：4 7；20 15 10 17

输出：15（解释：20-15=5，17-15=2，总木材 5+2=7）

题目分析

可行解空间：H 的最小值是 0（砍倒所有树），最大值是最高树木的高度（获得 0 米木材）。
可行性判断：对于给定的 H，计算所有树木高于 H 的部分总和（sum = max (树高 - H, 0)），若 sum≥M，则 H 是可行解。
二分目标：找最大的可行解 H（右边界）。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;typedef long long LL;// 可行性函数：高度为mid时，能否获得≥M米木材
bool isPossible(const vector<LL>& trees, LL M, LL mid) {LL total = 0;for (LL tree : trees) {if (tree > mid) {total += tree - mid;}// 剪枝：总和已足够，无需继续计算if (total >= M) return true;}return total >= M;
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n;LL M;cin >> n >> M;vector<LL> trees(n);LL max_tree = 0;for (int i = 0; i < n; i++) {cin >> trees[i];max_tree = max(max_tree, trees[i]);}// 可行解空间：left=0，right=最高树木高度LL left = 0, right = max_tree;LL ans = 0;while (left < right) {LL mid = left + (right - left + 1) / 2; // 找右边界if (isPossible(trees, M, mid)) {ans = mid;left = mid; // 尝试更高的高度} else {right = mid - 1; // 高度太高，降低范围}}cout << ans << endl;return 0;
}

思路总结

这道题的关键是 “可行性函数的计算”—— 只需累加树木高于 H 的部分。同时，由于树木高度可能很大（题目中树高≤4e5，n≤1e6），需要用long long避免溢出。二分的过程中，每次都向 “更优解” 的方向收缩，最终找到最大的 H。

例题 3：跳石头（洛谷 P2678）—— 进阶二分答案

题目链接：https://www.luogu.com.cn/problem/P2678

题目描述

在一条笔直的河道中，有起点、终点和 N 块岩石（起点和终点不移动）。组委会至多移走 M 块岩石，使得选手的最短跳跃距离尽可能长。求最短跳跃距离的最大值。

输入：

第一行：L（起点到终点的距离）、N（岩石数）、M（至多移走的岩石数）
接下来 N 行：每块岩石与起点的距离（按从小到大排序）

输出：最短跳跃距离的最大值

题目示例

输入：25 5 2；2；11；14；17；21输出：4（解释：移走 11 和 17 号岩石，跳跃距离为 2、3、4、4、12，最短距离为 2？不对，正确移法是移走 2 和 14 号岩石，跳跃距离为 11、3、4、7，最短距离为 3？实际正确输出是 4，需重新计算）

题目分析

问题转化：“最短跳跃距离的最大值” 是典型的二分答案场景。我们需要找到最大的 d，使得 “至少保留（N-M）块岩石” 的前提下，所有跳跃距离≥d。
可行解空间：d 的最小值是 1，最大值是 L（起点到终点的距离）。
可行性判断：对于给定的 d，计算需要移走的岩石数：
- 用两个指针 i 和 j，i 记录前一块保留的岩石位置，j 遍历当前岩石。
- 若当前岩石与 i 的距离 < d，说明需要移走当前岩石（移走计数 + 1）。
- 若距离≥d，说明保留当前岩石，更新 i 为 j。
- 最后，若移走计数≤M，则 d 是可行解。

代码实现

#include <iostream>
#include <vector>
using namespace std;typedef long long LL;// 可行性函数：最短跳跃距离为mid时，是否只需移走≤M块岩石
bool isPossible(const vector<LL>& stones, LL L, int M, LL mid) {int remove = 0; // 需要移走的岩石数LL prev = 0; // 前一块保留的岩石位置（起点）int n = stones.size();for (int i = 0; i < n; i++) {if (stones[i] - prev < mid) {// 距离不足，移走当前岩石remove++;} else {// 距离足够，保留当前岩石prev = stones[i];}// 剪枝：移走数已超过M，无需继续if (remove > M) return false;}// 最后检查终点与最后一块保留岩石的距离if (L - prev < mid) {remove++;}return remove <= M;
}int main() {ios::sync_with_stdio(false);cin.tie(0);LL L;int N, M;cin >> L >> N >> M;vector<LL> stones(N);for (int i = 0; i < N; i++) {cin >> stones[i];}// 可行解空间：left=1，right=LLL left = 1, right = L;LL ans = 0;while (left < right) {LL mid = left + (right - left + 1) / 2; // 找右边界if (isPossible(stones, L, M, mid)) {ans = mid;left = mid; // 尝试更大的距离} else {right = mid - 1; // 距离太大，缩小范围}}cout << ans << endl;return 0;
}

思路总结

这道题的难点是 “可行性函数的设计”—— 需要模拟岩石的保留和移走过程。关键是 “前一块保留的岩石位置” 的更新，以及最后检查终点与最后一块岩石的距离（容易遗漏）。通过二分答案，我们将 “求最优距离” 转化为 “判断距离是否可行”，时间复杂度从暴力枚举的 O (2^N)（不可能）优化到 O (N log L)，高效处理 N=5e4 的数据。

五、二分算法的常见误区与避坑指南

5.1 误区 1：认为二分只能用于有序数组

很多人以为 “二分必须基于有序数组”，这是对二分的片面理解。实际上：

二分查找确实需要有序数组（因为需要二段性）。
二分答案不需要数组有序，只需要 “可行解空间具有二段性”（如木材加工、砍树问题，数组可以是无序的，只需计算总和）。

例如，砍树问题中，树木的高度可以是无序的，我们只需要计算 “高度为 H 时的总木材”，不需要排序。

5.2 误区 2：边界处理不当导致死循环

最常见的错误是 “mid 计算错误” 或 “边界收缩错误”：

计算 mid 时用(left + right) / 2：当 left 和 right 很大时（如 1e9），会导致整数溢出，正确写法是left + (right - left) / 2。
找右边界时 mid 不加 1：导致 left 和 right 相差 1 时死循环（如left=1, right=2，mid=1，若可行则 left=1，永远循环）。

解决方法：严格遵守模板，找左边界 mid 不加 1，找右边界 mid 加 1。

5.3 误区 3：忘记判断结果的有效性

二分结束后，left不一定是可行解（比如目标值不存在于数组中），必须进行判断：

二分查找：判断nums[left]是否等于目标值（或满足条件）。
二分答案：判断isPossible(left)是否为真（比如木材加工中，left 可能是 0，需要判断是否能切出≥k 段）。

例如，在 “找第一个≥target 的元素” 中，若 target 比所有元素大，left会等于 n（数组长度），此时nums[left]会越界，必须提前判断。

5.4 误区 4：可行性函数效率太低

二分答案的时间复杂度是 O (log (right-left) × T)，其中 T 是可行性函数的时间复杂度。如果 T 太大（如 O (n²)），即使二分的 log 因子很小，总时间复杂度也会很高。

例如，跳石头问题中，可行性函数的时间复杂度是 O (n)，总时间复杂度是 O (n log L)，能处理 n=5e4 的数据；若可行性函数是 O (n²)，则会超时。

解决方法：优化可行性函数，确保 T 是 O (n) 或 O (n log n) 级别。

总结

二分算法是基础算法中的 “效率之王”，它用 O (log n) 的时间复杂度解决了很多看似需要暴力枚举的问题。无论是 “二分查找” 还是 “二分答案”，核心都是 “利用二段性缩小搜索范围”。

最后，送给大家一句话：二分算法的本质是 “聪明地排除不可能”，它教会我们 —— 解决问题不需要遍历所有可能，只需要找到关键的分界点，就能快速定位答案。希望通过本文的讲解，你能真正吃透二分算法，在未来的算法竞赛和面试中，用它攻克更多难题！

查看全文

http://www.dtcms.com/a/600967.html