【ZeroRange WebRTC】ECDHE 底层原理与在 TLS 中的应用（深入解析）

ECDHE 底层原理与在 TLS 中的应用（深入解析）

本文从数学与工程两个层面讲解 ECDHE（Elliptic Curve Diffie‑Hellman Ephemeral，椭圆曲线临时密钥协商）：曲线与运算、共享秘密的生成、前向保密的来源，以及 ECDHE 在 TLS 1.3 密钥日程中的实际位置。

---

目录

• 概览：为什么选择 ECDHE
• 数学基础：椭圆曲线与点运算（加法/标量乘法）
• 协商流程：双方生成临时密钥并交换公钥，计算共享秘密
• 安全性质：离散对数难题与前向保密（PFS）
• 在 TLS 中的应用：从 ECDHE 到 HKDF，再到记录层 Key/IV/Nonce
• 实践建议：曲线选择、密钥长度、实现注意事项
• 图示：握手时序、曲线运算、TLS 密钥映射

---

概览：为什么选择 ECDHE

• 计算效率高：与传统 DH/RSA 相比，ECC 在较短密钥长度下提供同等级安全性。
• 前向保密：使用“临时密钥对”（Ephemeral），每个会话独立；长期密钥泄露不会解密过去会话。
• 现代标准：TLS 1.3 仅支持具前向保密的密钥交换（ECDHE/PSK），弃用不具 PFS 的 RSA 握手。

---

数学基础：椭圆曲线与点运算

• 椭圆曲线（有限域上）：满足方程 y^2 = x^3 + ax + b (mod p) 的点集合（加上无穷远点）。
• 点加法与倍点：几何直观（过两点作直线，与曲线再相交并镜像），在有限域上转化为模运算。
• 标量乘法：Q = k * G，把基点 G 叠加 k 次得到点 Q；构成“椭圆曲线离散对数问题（ECDLP）”。
• 安全性来源：给定 G 与 Q 很难求出标量 k（NP 难度范畴），这保证密钥难以从公钥反推回私钥。

---

协商流程：生成共享秘密

• 双方生成临时密钥对：
  • 客户端：随机选取私钥 a，计算公钥 A = a * G。
  • 服务端：随机选取私钥 b，计算公钥 B = b * G。
• 交换公钥（KeyShare）：
  • 客户端在 ClientHello 中发送 A；服务端在 ServerHello 中发送 B。
• 计算共享秘密：
  • 客户端计算 S = a * B = a * (b * G)；
  • 服务端计算 S = b * A = b * (a * G)；
  • 因为标量乘法交换律，双方得到相同点 S。
• 注意：共享秘密 S 不直接用作对称密钥，而是作为 HKDF 的输入（与握手抄本一起）。

---

安全性质：离散对数与前向保密

• 离散对数难题（ECDLP）：给定 G 与 A = a * G，从 A 求出 a 计算复杂度极高（在恰当参数下不可行）。
• 前向保密（PFS）：临时私钥 a/b 仅在当前会话使用并销毁；即使长期私钥泄露，历史会话的共享秘密仍不可得。
• 抵御被动监听与中间人：配合证书校验（验证服务端身份）与 Finished MAC（绑定握手抄本），确保共享秘密与握手内容不可篡改。

---

在 TLS 中的应用：从 ECDHE 到 HKDF，再到记录层

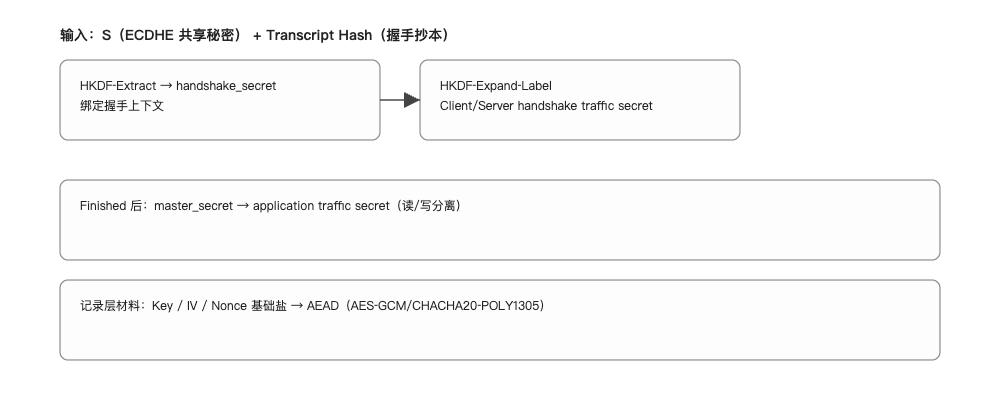
• 输入：ECDHE 共享秘密 S + 握手抄本哈希（Transcript Hash）。
• HKDF‑Extract/Expand：
  • 提取基础密钥（handshake_secret），再派生读/写方向的 handshake traffic secret；
  • 完成 Finished 后，从 master_secret 派生应用阶段的 application traffic secret。
• 记录层材料：
  • 从各自的 traffic secret 派生对称 Key/IV/Nonce 基础盐，使用 AEAD（AES‑GCM/CHACHA20‑POLY1305）保护 HTTP/WSS 数据。
• KeyUpdate：支持长期连接的重钥（re‑key），降低密钥长期使用的风险。

---

实践建议

• 曲线选择：优先使用 X25519 或 P‑256（广泛支持且性能强）；避免已弃用或弱参数曲线。
• 随机数质量：临时私钥由 CSPRNG（安全随机源）生成；避免重复或低熵导致私钥碰撞。
• 实现注意：常数时间标量乘法、防侧信道（如计时/缓存观察）、正确处理公钥验证（点是否在曲线上、非零点）。
• 证书与握手绑定：确保证书链与主机名校验通过、Finished MAC 验证成功，防止中间人攻击。

---