当前位置：首页 > news >正文

2023年INS SCI2区，演化状态驱动的多群体合作粒子群算法用于复杂优化问题，深度解析+性能实测

news 2025/11/10 8:38:15

1.摘要

粒子群算法（PSO）已广泛应用于解决各种实际工程问题，但存在诸如早熟收敛和较差的全局搜索能力等不足。为了解决这些问题，论文提出了一种演化状态驱动的多群体合作粒子群算法（ESD-PSO），该算法采用自适应多群体合作机制（AMC）来提高各子群体之间的信息交换效率。在AMC中，种群被随机分为多个等大小的子群体，每个子群体的最佳粒子用于评估其演化状态。当出现多个停滞子群体且数量达到阈值时，所有子群体将自适应地重新组合。此外，如果某个子群体长时间停滞且未达到重新组合条件，则触发停滞补偿策略（SCS）以增强停滞子群体的多样性。在这种情况下，生成补偿样本以帮助停滞的子群体重新搜索有前景的区域，竞争性干扰机制（CDM）用于提高解的精度。

2.演化状态驱动的多群体合作粒子群算法

自适应多群体合作机制（AMC）

Schematic diagram of the adaptive multi-swarm cooperation mechanism

为保持种群多样性并提高优化效率，论文提出了自适应多群体合作策略（AMC），该策略通过将种群随机分为多个子群体，并根据演化状态自适应重组，确保适度的信息交换，避免过早收敛或效率低下。
$V_{i,j}^{d}(t+1)=w^{*}V_{i,j}^{d}(t)+c_{1}^{*}r_{1}^{*}(pbest_{i,j}^{d}(t)-X_{i,j}^{d}(t))+c_{2}^{*}r_{2}^{*}(lbest_{j}^{d}(t)-X_{i,j}^{d}(t))$

通过监控最佳粒子变化量来评估子群体的演化状态，若停滞，则通过停滞因子判断是否触发重组。若停滞子群体比例超过阈值S，则对停滞子群体进行自适应重组，以避免局部最优，其他子群体保持不变。

停滞补偿策略（SCS）

当全体种群未达到重组条件时，若某子群体的停滞因子大于K，则触发停滞补偿策略（SCS），以帮助其重新搜索有前景的区域。SCS通过从种群的优秀历史信息中构建补偿样本，增加多样性和精英信息，补充停滞子群体的搜索能力。在每代中，从所有粒子的个人历史最佳解中随机选择两个粒子，生成一个新的活力粒子。
$\begin{array} {c}pbest_1,pbest_2,pbest_3,\cdots,pbest_N \end{array})$
$e_j^d(t)=gbest^d(t)+F^*(E_{r1}^d(t)-E_{r2}^d(t))$

竞争性干扰机制（CDM）

在搜索过程中， $g_{best}$ 对所有粒子具有主导作用，若处于局部最优，整个种群会陷入局部最优，导致早熟收敛。竞争性干扰机制（CDM）帮助 $g_{best}$ 逃脱局部最优。所有粒子的历史最佳信息的平均值：
$Mpbest^d(t)=(\frac{1}{N}\sum_{i=1}^{N}pbest_{i}^{1}(t),\frac{1}{N}\sum_{i=1}^{N}pbest_{i}^{2}(t),\cdots,\frac{1}{N}\sum_{i=1}^{N}pbest_{i}^{D}(t))$

在CDM中，利用整个种群的历史优秀信息来寻找有前景的区域：
$Nbest^d(t)=r^*gbest^d(t)+(1-r)(gbest^d(t)-Mpbest^d(t))$

3.结果展示

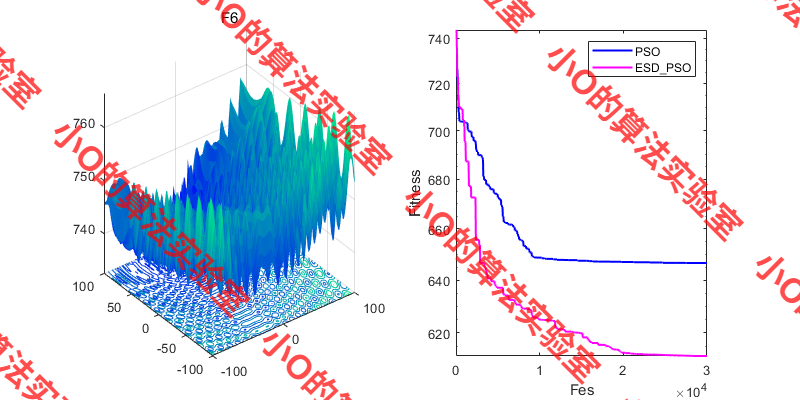
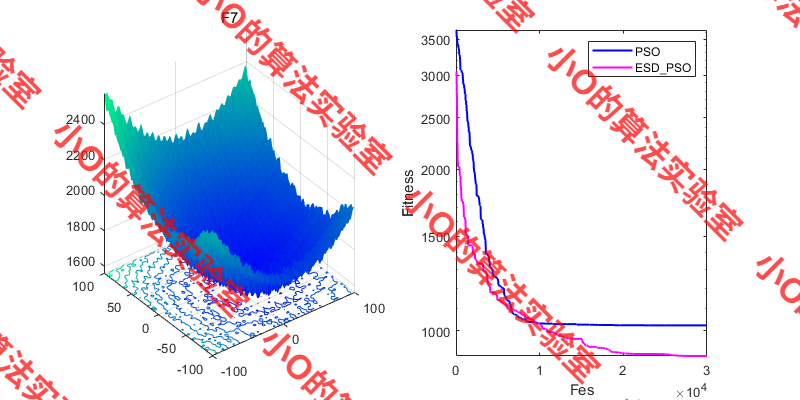
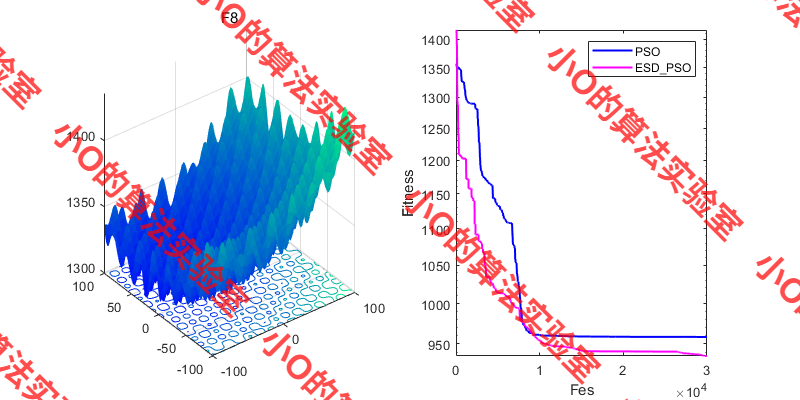
4.参考文献

[1] Yang X, Li H. Evolutionary-state-driven multi-swarm cooperation particle swarm optimization for complex optimization problem[J]. Information Sciences, 2023, 646: 119302.