【自用】Python二分查找写法

1. 元素下标

对于数组[1, 2, 3, 4, 5, 5, 5, 5, 6, 7]，查找

①＜5 的最后一个元素下标

② ≥5 的第一个元素下标

③ ≤5 的最后一个元素下标

④＞5 的第一个元素下标

下面先利用库函数来理解四个问题的转换关系，然后给出一种库函数二分原理的具体写法。

---

库函数写法1：

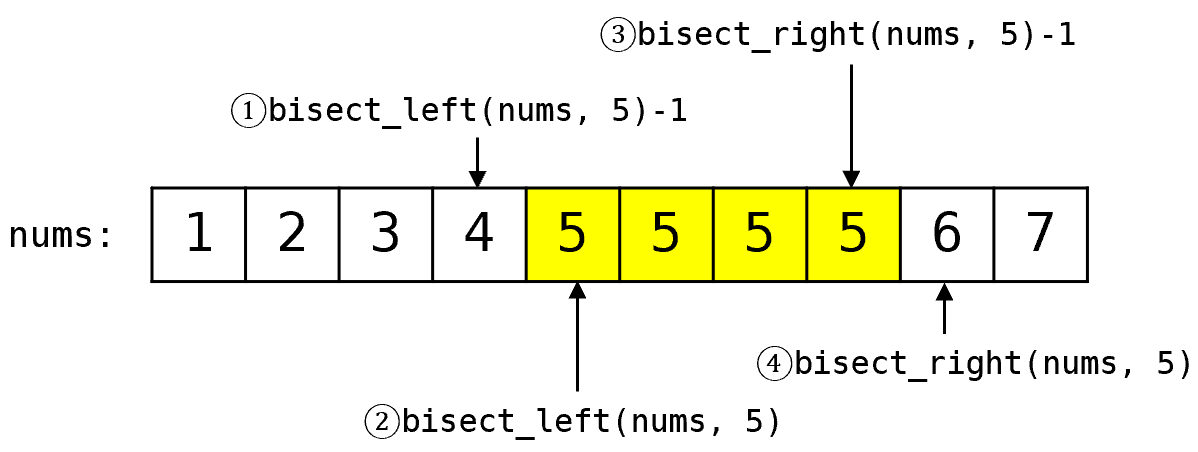
python中 a = bisect_left(nums, x) 和 b = bisect_right(nums, x) 可以找到 [a, b) 范围内的数 == x。

即 a 是大于等于 x 的第一个元素下标，b 是大于 x 的第一个元素下标，如下图②④。

两个函数返回值的范围都是 [0, len(nums)] 闭区间。

库函数写法2：

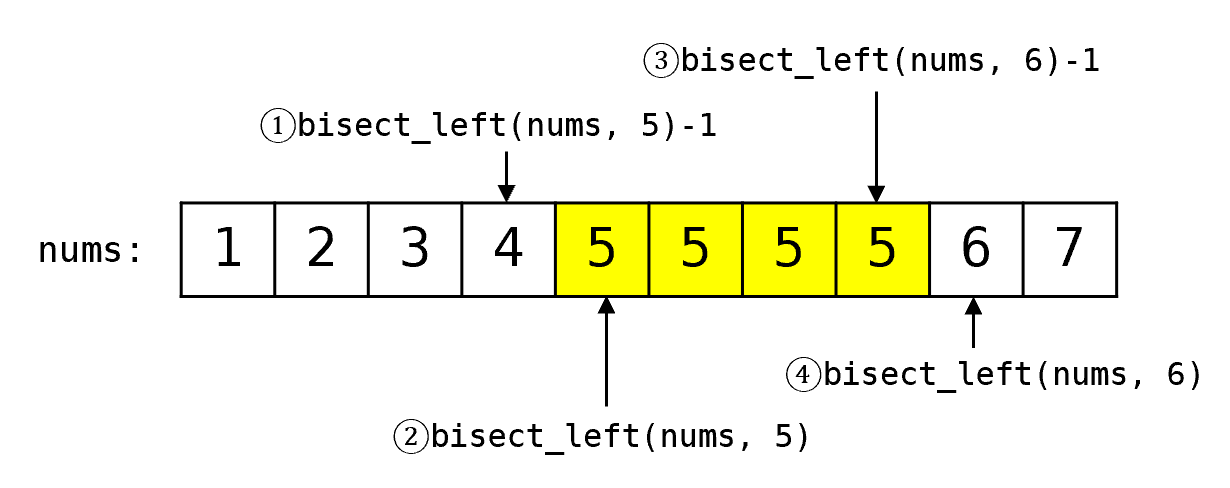
不用 bisect_right，只用 bisect_left。

对于整数数组，大于 x 的第一个元素即大于等于 x+1 的第一个元素，下图改变了③④。

库函数的方法重在转换，省略了核心的二分过程，下面提供分别提供二分原理的一种写法。

二分写法：

这里的lower_bound()和upper_bound()与bisect_left()和bisect_right()含义相同。

def lower_bound(nums: List[int], target: int):# >=target的第一个i, j = -1, len(nums)while i + 1 < j:mid = (i + j) // 2if nums[mid] < target:i = midelse:j = midreturn jdef upper_bound(nums: List[int], target: int):# >target的第一个i, j = -1, len(nums)while i + 1 < j:mid = (i + j) // 2if nums[mid] <= target:i = midelse:j = midreturn j

👆两个函数只有 if 判断条件有区别。两个函数的返回值范围都是 [0, len(nums)] 闭区间。

其中，当nums为整数数组时， 有upper_bound(nums, x) = lower_bound(nums, x+1)。

分别解决了②和④，然后套用库函数法中的转换关系解决①③。

我们还可以不转换直接写出①③的二分代码：只需要将 lower_bound 和 upper_bound 的返回值改为 i 即可，因为最后退出循环时 i + 1 == j。此时两个函数的返回值范围是 [-1, len(nums)-1] 闭区间。

---

2. 元素个数

对于数组[1, 2, 3, 4, 5, 5, 5, 5, 6, 7]，求

①＜5 的元素个数

② ≥5 的元素个数

③ ≤5 的元素个数

④＞5 的元素个数

⑤ ==5 的元素个数

因为求个数完全可以用求下标的函数转换过来，所以下面只提供转换关系：

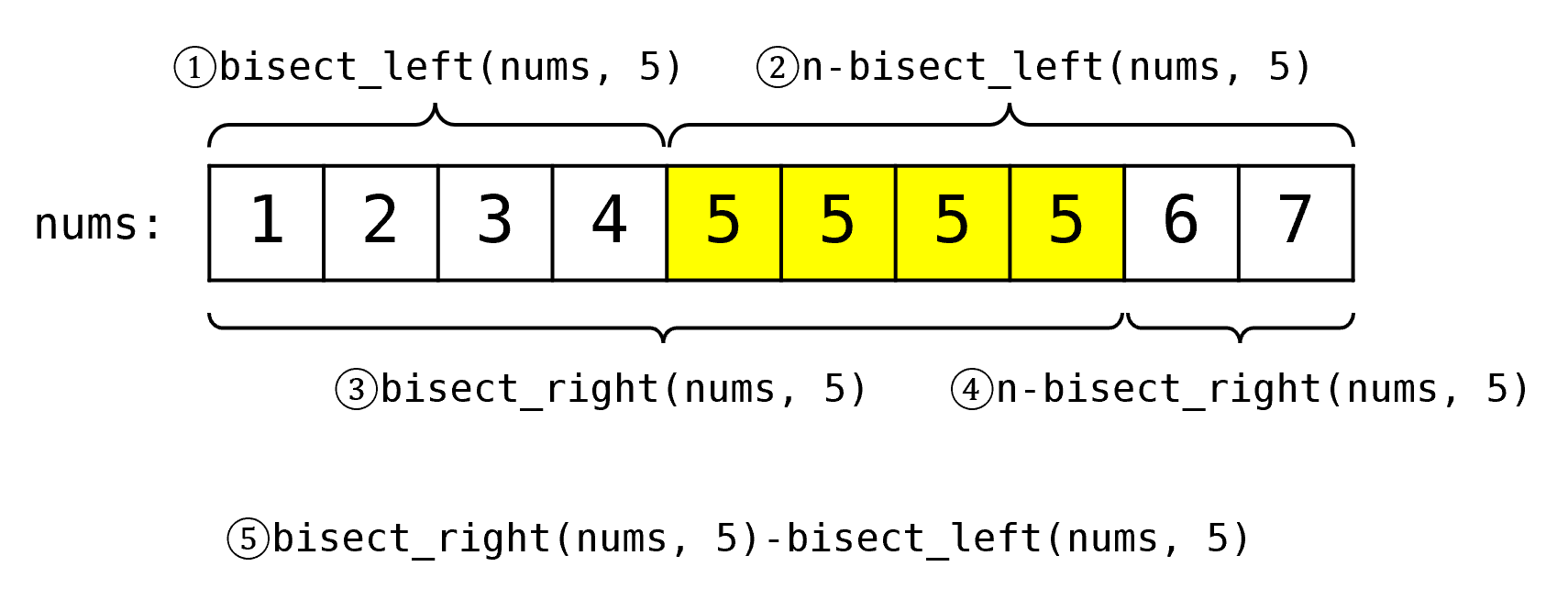
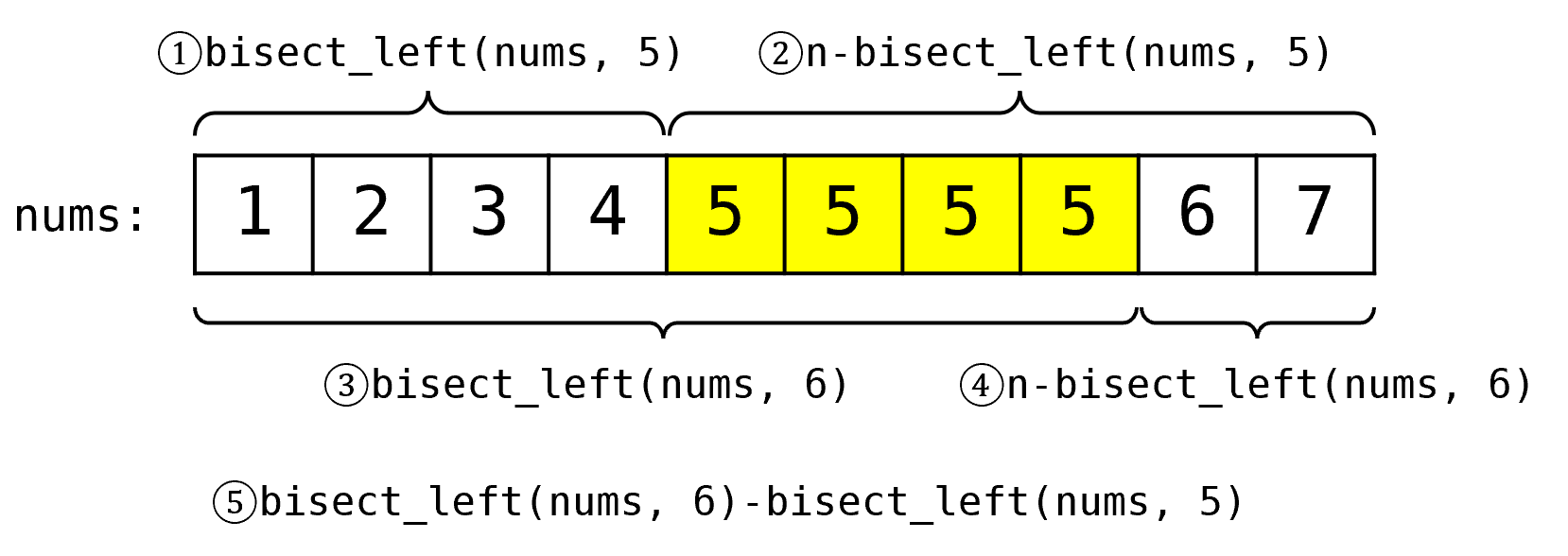
其中n = len(nums)，⑤=③-①。如果不用bisect_right()的话：

---

总结

bisect_left(nums, x)： ≥x 的第一个元素下标， <x 的元素个数；

bisect_right(nums, x)： >x 的第一个元素下标， ≤x 的元素个数。

对于整数，bisect_right(nums, x) = bisect_left(nums, x+1)。

元素下标	转换关系
≥x的第一个	bisect_left(nums, x)
>x的第一个	bisect_right(nums, x)	bisect_left(nums, x+1)
<x的最后一个	bisect_left(nums, x) - 1
≤x的最后一个	bisect_right(nums, x) - 1	bisect_left(nums, x+1) - 1

元素个数	转换关系
<x	bisect_left(nums, x)
≥x	n - bisect_left(nums, x)
≤x	bisect_right(nums, x)	bisect_left(nums, x+1)
>x	n - bisect_right(nums, x)	n - bisect_left(nums, x+1)
==x	bisect_right(nums, x) - bisect_left(nums, x)	bisect_left(nums, x+1) - bisect_left(nums, x)