OpenCV(二十一)：图像的放大与缩小

图像放大与缩小的原理

图像放大（Zoom In）与缩小（Zoom Out）是空间域插值（Spatial Interpolation）的典型操作，本质上是对图像的像素重采样（Resampling）。

当你调整图像尺寸时，OpenCV 使用不同的**插值算法（Interpolation Methods）**计算新像素的灰度或颜色值。

空间域插值

定义

空间域插值 是指：
在图像的空间坐标系（x, y）上，对已知像素间的未知位置进行像素值估计的过程。

简单来说：

当图像被放大、旋转或扭曲后，新生成的像素点往往位于原图像的“两个像素之间”，此时我们需要通过插值算法估计这些新像素的值。

“空间域”

“空间域（Spatial domain）”指的是图像的像素空间坐标表示形式。
与之相对的是“频率域（Frequency domain）”，例如用傅里叶变换表示图像。

域类型	操作对象	典型算法	应用
空间域	像素坐标 (x, y)	最近邻、双线性、双三次	缩放、旋转、平移
频率域	频率坐标 (u, v)	卷积、滤波	去噪、锐化、增强

核心思想

当我们进行缩放或变换时，新像素点 (x', y') 通常落在原图中的非整数位置 (x, y)。
由于原图只有整数像素点，因此需要“插值”计算该位置的灰度值。

常见公式如下（以双线性插值为例）：

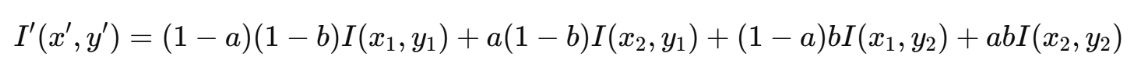
其中：

• (x_1, y_1), (x_2, y_1), (x_1, y_2), (x_2, y_2) 是原图中相邻的 4 个像素；
• a, b 是目标点在 x、y 方向的小数部分；
• I'(x', y') 是新图像中该点的像素值。

这就是在空间域上“插”出新的像素值的过程。

像素重采样

定义

图像重采样 是指：

在几何变换或尺寸变化后，对图像进行重新取样（Sampling），即计算新像素网格对应的原始像素值的过程。

换句话说：

• “采样”是从原图获取像素；
• “重采样”是重新计算像素分布，使图像适应新的尺寸或坐标系。

重采样的两个核心步骤

坐标映射（Coordinate Mapping）

确定新图像中每个像素点 (x', y') 在原图中对应的坐标 (x, y)：

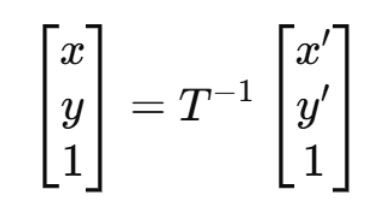
这里 T−1 是几何变换矩阵的逆矩阵。
比如缩放、旋转、透视变换等。

插值计算（Interpolation）

在原图中 (x, y) 一般不是整数坐标，因此需要使用 空间域插值算法（如双线性、双三次等）来计算该点的像素值。

重采样的类型

类型	操作	示例
下采样（Down-sampling）	减少像素数	图像缩小
上采样（Up-sampling）	增加像素数	图像放大
任意几何变换重采样	改变图像形状	旋转、透视变换、投影映射

空间域插值 vs 图像重采样

对比点	空间域插值	图像重采样
含义	对连续空间中的像素值进行估计	重新建立新的像素网格并计算像素值
作用范围	单像素计算方法	整体几何变换过程
是否依赖几何映射	否（局部算法）	是（全局过程）
包含关系	属于重采样的核心步骤	包含插值作为关键环节
举例	双线性、双三次	图像缩放、旋转、透视校正

可以这样理解：

图像重采样 = 坐标映射 + 空间域插值

重采样中的问题：混叠（Aliasing）

当图像缩小时，如果不对高频信号（细节）进行滤波，会出现“波纹状伪影”，称为混叠。
cv2.INTER_AREA 插值法正是通过对像素区域求平均来抑制混叠的典型方法。

插值算法原理

OpenCV 提供多种插值方式，通过 cv2.resize() 的 interpolation 参数选择：

插值算法	参数名	适用场景	原理说明
最近邻插值	cv2.INTER_NEAREST	速度最快、质量最低	新像素取最近的原像素值（阶梯状锯齿明显）
双线性插值	cv2.INTER_LINEAR	默认方式，适合放大	用 2×2 像素的加权平均
双三次插值	cv2.INTER_CUBIC	高质量放大，慢	用 4×4 像素块的三次卷积计算
区域插值	cv2.INTER_AREA	缩小时效果最佳	取邻域像素的平均值（避免锯齿）
Lanczos 插值	cv2.INTER_LANCZOS4	超高质量放大	基于 sinc 函数的高阶插值

最近邻插值（Nearest Neighbor Interpolation）

原理：

• 对于新像素 (x', y')，找到离它最近的原像素 (x, y)。
• 直接复制该像素的值。

公式：

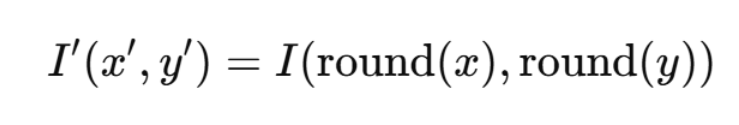
特点：

• 不进行平滑或权重计算。
• 最快，但锯齿感严重。

适用场景：

• 分类图（如标签图、掩码图），不希望像素混合。
• 实时视频预览。

OpenCV参数： cv2.INTER_NEAREST

双线性插值（Bilinear Interpolation）

原理：

• 新像素取自其周围 2×2 区域像素的加权平均。
• 权重根据距离线性变化。

公式：

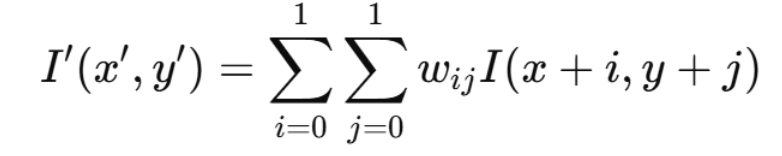
其中

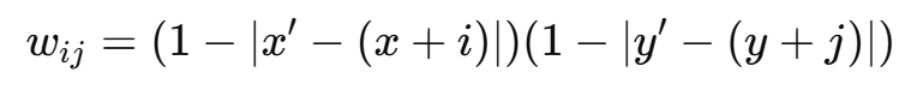
特点：

• 平滑过渡，锯齿少。
• 适合中等质量要求的放大。

OpenCV参数： cv2.INTER_LINEAR

双三次插值（Bicubic Interpolation）

原理：

• 使用 4×4 邻域像素（共16个点）进行加权平均。
• 权重由三次多项式函数确定。

常见核函数（Cubic kernel）：

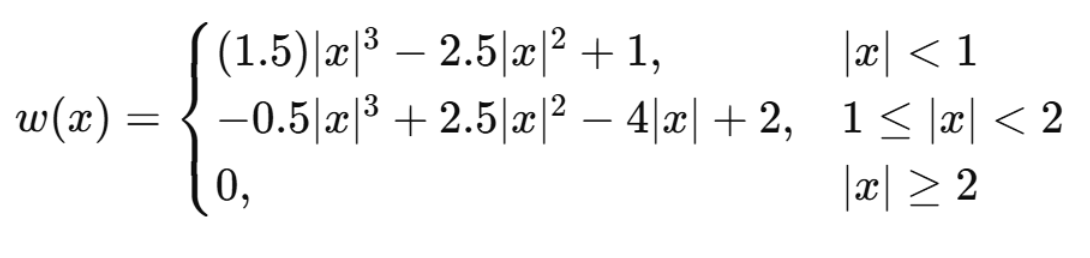
特点：

• 过渡更平滑，细节保持更好。
• 计算复杂度高于双线性。

适用场景：

• 高质量放大、照片增强、AI预处理。

OpenCV参数： cv2.INTER_CUBIC

区域插值（Area Interpolation）

原理：

• 新像素的值为原图中对应区域的平均值（积分平均）。
• 特别适合下采样（缩小）操作。

效果：

• 消除锯齿，防止混叠（aliasing）。
• 不适合放大，因为信息会模糊。

适用场景：

• 图像缩小、视频缩略图生成。

OpenCV参数： cv2.INTER_AREA

Lanczos 插值（Lanczos Interpolation）

原理：

• 基于 sinc 函数的高精度插值。
• 使用更宽的邻域（一般为 8×8）。
• 函数形式：

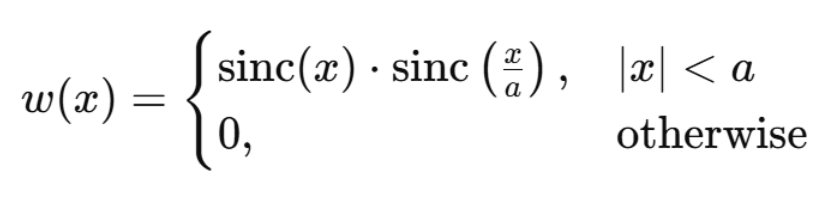
其中 a 通常取 3 或 4（对应 INTER_LANCZOS4）。

特点：

• 图像锐度和细节保持最佳。
• 计算量最大，速度最慢。

适用场景：

• 高质量图像缩放、照片编辑、打印前处理。

OpenCV参数： cv2.INTER_LANCZOS4

样条插值（Spline Interpolation，非OpenCV默认）

原理：

• 使用高阶多项式曲线拟合像素变化。
• 可实现平滑度更高的结果。

常见形式：

• 三次B样条（B-spline）
• Catmull-Rom样条

优点：

• 连续一阶、二阶导数，图像平滑。

缺点：

• 对边缘模糊敏感，不常用于实时计算。

效果与性能对比

插值算法	邻域大小	平滑性	保真度	速度	典型用途
最近邻	1×1	❌	差	🚀🚀🚀🚀🚀	掩码、实时预览
双线性	2×2	✅	一般	🚀🚀🚀🚀	通用缩放
双三次	4×4	✅✅	好	🚀🚀🚀	高质量放大
区域插值	自适应	✅	优	🚀🚀	图像缩小
Lanczos	8×8	✅✅✅	极优	🚀	精准放大
样条插值	4×4~6×6	✅✅✅	优	🚀🚀	图像重建

示例

import cv2
import matplotlib.pyplot as plt# 设置中文字体（Windows 常用字体为 SimHei；Mac 可用 PingFang）
plt.rcParams['font.sans-serif'] = ['SimHei']    # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False       # 正常显示负号# 1. 读取并转换颜色空间
img = cv2.imread("test.jpg")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)# 获取原始尺寸
h, w = img.shape[:2]
print(f"原始尺寸: {w} x {h}")# 2. 定义插值算法
methods = {"Nearest": cv2.INTER_NEAREST,"Linear": cv2.INTER_LINEAR,"Cubic": cv2.INTER_CUBIC,"Area": cv2.INTER_AREA,"Lanczos": cv2.INTER_LANCZOS4
}# 3. 图像放大（2 倍）
resized_up = {}
for name, method in methods.items():resized_up[name] = cv2.resize(img, None, fx=2, fy=2, interpolation=method)# 4. 图像缩小（0.5 倍）
resized_down = {}
for name, method in methods.items():resized_down[name] = cv2.resize(img, None, fx=0.5, fy=0.5, interpolation=method)# 5. 使用 Matplotlib 显示结果
plt.figure(figsize=(14, 8))# 第一行：放大效果
for i, (name, image) in enumerate(resized_up.items(), 1):plt.subplot(2, len(methods), i)plt.imshow(image)plt.title(f"放大 x2 - {name}")plt.axis('off')# 第二行：缩小效果
for i, (name, image) in enumerate(resized_down.items(), 1):plt.subplot(2, len(methods), i + len(methods))plt.imshow(image)plt.title(f"缩小 x0.5 - {name}")plt.axis('off')plt.suptitle("OpenCV 各类插值算法：放大 vs 缩小 效果对比", fontsize=16)
plt.tight_layout()
plt.show()

执行效果：