Similarity and Dissimilarity Measures|相似性和不相似性度量
-----------------------------------------------------------------------------------------------
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
----------------------------------------------------------------------------------------------
一、引言

在数据挖掘和机器学习中,衡量两个数据对象之间的“相似”或“不同”是非常重要的一步。无论是进行聚类分析、分类预测,还是构建推荐系统,我们都需要一种方法来量化数据之间的关系,也就是判断它们到底有多像或者多不像。这种量化方式,便是通过“相似性(Similarity)”和“不相似性(Dissimilarity)”度量来实现的。
相似性度量用于表示两个对象的相似程度,而不相似性度量则反映它们之间的差异程度。二者本质上是相对的:当两个数据对象越相似时,它们的相似度值越高,而不相似度值就越低。这些度量方法构成了许多算法的数学基础,比如K-Means聚类、K近邻分类(KNN)等,几乎贯穿于整个数据分析过程。
在现实应用中,这种“相似”与“不同”的度量并不仅仅是数学概念,更是模型性能和结果精度的重要影响因素。例如,在图像识别中,通过相似性度量可以判断两张图片是否属于同一对象;在推荐系统中,可以根据相似性寻找兴趣相近的用户,从而提供个性化推荐。因此,理解并掌握相似性与不相似性度量,不仅是学习算法的基础,更是将理论应用到实际问题中的关键一步。
二、相似性度量
相似性度量(Similarity Measure)是用来衡量两个数据对象之间“相似程度”的一种数值化指标。它的核心思想是:当两个对象越相似时,相似度的数值就越大。通常情况下,相似度的取值范围在 [0, 1] 之间,其中 1 表示完全相同,0 表示完全不相似。通过这种方式,我们能够把抽象的“相似”概念转化为可计算的数学形式。
在实际计算中,相似性度量可以有多种实现方式。对于数值型数据,常见的方法包括余弦相似度(Cosine Similarity)和皮尔逊相关系数(Pearson Correlation Coefficient)。余弦相似度通过计算两个向量之间的夹角来判断它们是否相似,当夹角越小,相似度越高;而皮尔逊相关系数则反映两组数据在变化趋势上的一致性。对于文本数据或离散特征,也可以使用Jaccard 相似系数来比较集合的重合程度。
在数据分析的不同场景中,相似性度量的选择会影响最终的结果。例如,在推荐系统中,如果选择余弦相似度,就更强调用户兴趣向量的方向一致性;而在社交网络分析中,使用Jaccard系数则更关注用户间共同好友或共同兴趣的比例。可以说,相似性度量的设计不仅决定了计算方式,也反映了我们对“相似”的定义和理解。
总的来说,相似性度量是一种桥梁,它让抽象的数据关系得以被数学化、量化,从而为各种算法提供了判断基础。无论是分类、聚类还是检索任务,合理的相似性度量都是模型取得良好效果的重要前提。
三、不相似性度量
不相似性度量(Dissimilarity Measure),也常被称为“距离度量(Distance Measure)”,用于衡量两个数据对象之间的差异程度。与相似性度量相反,它表示的是两个对象之间“有多不同”。通常情况下,不相似性的数值越大,说明两个对象之间的差异越明显;反之,数值越小,则说明它们越接近。
最常见的不相似性度量方法是欧氏距离(Euclidean Distance),它通过计算两点在空间中的直线距离来衡量差异,是几何意义上最直观的一种度量方式。除此之外,还有曼哈顿距离(Manhattan Distance),它通过坐标轴方向上的绝对差值之和来计算距离,更适合描述格点型或高维稀疏数据的差异。而对于具有相关性或不同尺度的特征,马氏距离(Mahalanobis Distance)可以考虑变量间的协方差关系,从而更准确地衡量复杂数据之间的差异。
在实际应用中,不相似性度量是许多算法的核心。例如,K-Means聚类通过计算样本点之间的欧氏距离来划分簇中心;K近邻分类(KNN)则根据距离最近的样本类别来进行预测;在图像识别中,距离度量也常用于衡量特征向量之间的差异。不同的距离公式会导致模型行为的变化,因此选择合适的距离度量往往需要结合数据特点和任务需求进行权衡。
总体来看,不相似性度量提供了一种判断“差异”的方式。它不仅帮助我们理解数据之间的结构关系,也为算法提供了量化依据。可以说,如果没有这些距离度量的支撑,很多机器学习算法都无法正常运作。
四、相似性与不相似性的关系
相似性和不相似性虽然名称不同,但在数学意义上它们是可以相互转换的。二者共同构成了衡量数据关系的两种基本方式,就像“近”和“远”是对空间距离的两种描述一样,前者强调相似,后者强调差异。理解它们之间的关系,有助于我们在不同算法中更灵活地使用这两种度量。
一般来说,相似性度量和不相似性度量可以通过简单的线性变换来相互转换。例如,如果相似度的取值范围是 [0,1][0,1],那么我们可以用公式
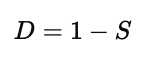
将相似度 S 转换为不相似度 D。反过来,如果距离(不相似性)越小表示越相似,那么可以用

将距离转化为相似度。这样的关系使得算法能够在不同视角下对数据进行处理,而不会改变其本质的比较逻辑。
在算法设计中,这种相互转换非常实用。例如,聚类算法多使用“距离”来衡量样本间的关系,而推荐系统更倾向使用“相似度”来找出相近的用户或物品。其实,它们底层的思想是相通的:距离小代表相似度高,只是表现形式不同。
此外,在实际问题中,相似性与不相似性往往需要归一化处理,以消除量纲和数值范围的影响,从而使得不同特征之间的比较更加公平和准确。
五、实际应用
相似性与不相似性度量在数据科学与人工智能的各个领域中都有着广泛的应用。它们几乎贯穿了整个数据分析的过程,从数据预处理、特征提取到模型构建和结果评估,都离不开这两类度量的支持。
在聚类分析中,不相似性度量(尤其是距离度量)是算法的核心。例如,K-Means聚类算法通过计算样本之间的欧氏距离,将距离较近的样本归为同一簇。距离越小,样本之间的差异越小,说明它们属于同一类别的可能性越大。类似地,层次聚类算法也是基于不相似性度量来逐步合并或划分样本的。
在推荐系统中,相似性度量发挥着关键作用。通过计算用户之间或物品之间的相似度,系统可以为用户推荐可能感兴趣的内容。例如,基于余弦相似度的协同过滤算法,可以找出兴趣向量方向相近的用户,从而实现个性化推荐。这种基于“相似行为”的推荐逻辑,让系统能够在信息繁杂的环境中提供更符合用户需求的结果。
在图像识别与文本分析等领域,相似性与不相似性度量同样重要。图像检索系统中,可以通过特征向量之间的距离来判断图片是否属于同一对象;而在自然语言处理中,文本相似度可用于语义匹配、情感分析等任务。通过计算文本向量之间的相似性,模型能够理解不同句子之间的语义关系,实现更智能的语言理解。
除此之外,异常检测、社交网络分析、生物信息学等领域也广泛应用了相似性和不相似性度量。例如,在异常检测中,通过比较样本与整体数据的差异,可以发现异常点;在生物序列分析中,衡量基因序列间的相似度有助于研究进化关系。
可以说,无论是哪一种数据类型,相似性与不相似性度量都为数据的“比较”提供了数学基础。它们让抽象的信息变得可量化,为各种智能算法提供了判断依据,也让我们能够更好地理解数据背后的模式和结构。
六、总结
相似性与不相似性度量是数据分析与机器学习中最基础却最重要的概念之一。它们为我们提供了一种量化数据关系的方式,使得计算机能够理解“相似”与“不同”这类抽象的概念。无论是聚类、分类、推荐还是文本分析,这两种度量方法都在其中扮演着关键角色。
相似性度量帮助我们找到相近的对象,从而实现更高效的匹配与推荐;不相似性度量则帮助我们识别差异与边界,使模型能够更准确地划分类别或发现异常。虽然二者从表达形式上是相反的,但在数学和逻辑上却密不可分,可以通过简单的变换互相转化。它们的结合,使得算法在不同任务中都能灵活适应,既能发现数据之间的共同点,也能捕捉潜在的差异。
从更广的角度来看,相似性与不相似性度量不仅仅是一种计算手段,更体现了我们认识和分析世界的方式。在数据驱动的时代,能够有效地度量“相似”和“不同”,就意味着能够更准确地洞察数据背后的规律。因此,深入理解这两种度量方法,不仅有助于掌握各类算法原理,更是构建高质量智能系统的重要前提。
-----------------------------------------------------------------------------------------------
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
----------------------------------------------------------------------------------------------
